1.4 角平分线同步练习（含解析）

1.7角平分线
姓名：__________________ 班级：______________ 得分：_________________
注意事项：
本试卷满分100分，试题共24题，选择10道、填空8道、解答6道．答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置．
一、选择题（本大题共10小题，每小题3分，共30分）在每小题所给出的四个选项中，只有一项是符合题目要求的．
1．（2019秋?黑河期末）如图，∠MON＝60°，OA平分∠MON，P是射线OA上的一点，且OP＝4，若点Q是射线OM上的一个动点，则PQ的最小值为（　　）
A．1 B．2 C．3 D．4
2．（2020春?昭通期末）如图，OP平分∠AOB，PD⊥OA于点D，点E是射线OB上的一个动点，若PD＝3，则PE的最小值（　　）
A．等于3 B．大于3 C．小于3 D．无法确定
3．（2020秋?慈溪市期中）如图，E为∠BAC平分线AP上一点，AB＝4，△ABE的面积为12，则点E到直线AC的距离为（　　）
A．3 B．4 C．5 D．6
4．（2020春?济阳区期末）如图，已知△ABC中，∠C＝90°，AD平分∠BAC，且CD：BD＝3：4．若BC＝21，则点D到AB边的距离为（　　）
A．7 B．9 C．11 D．14
5．（2020秋?定西期末）如图，在四边形ABCD中，∠A＝90°，AD＝4，连接BD，BD⊥CD，∠ADB＝∠C．若P是BC边上一动点，则DP长的最小值为（　　）
A．4 B．3 C．2 D．1
6．（2020春?南海区期末）如图，射线OC是∠AOB的角平分线，D是射线OC上一点，DP⊥OA于点P，DP＝4，若点Q是射线OB上一点，OQ＝3，则△ODQ的面积是（　　）
A．3 B．4 C．5 D．6
7．（2020秋?江北区校级期中）如图，在△ABC中，∠BAC＝90°，AD是BC边上的高，BE是AC边的中线，CF是∠ACB的角平分线，CF交AD于点G，交BE于点H，下面说法正确的是（　　）
①△ABE的面积＝△BCE的面积；②∠FAG＝∠FCB；③AF＝AG；④BH＝CH．
A．①②③④ B．①②③ C．②④ D．①③
8．（2020春?灯塔市期末）如图，在△ABC中，分别以点A，B为圆心，大于12AB长为半径作弧，两弧交于点M，N，作直线MN分别交AB，AC于点D，E，连接BE，下列结论错误的是（　　）
A．AD＝BD B．∠BEC＝2∠DBE C．AE＝BE D．BE平分∠CBD
9．（2020秋?松山区期末）如图所示，在△ABC中，∠ACB＝90°，BE平分∠ABC，DE⊥AB于点D，如果AE+DE＝3cm，那么AC等于（　　）
A．2cm B．3cm C．4cm D．5cm
10．（2020春?渭滨区期末）如图，AE是△ABC的角平分线，AD⊥BC于点D，点F为BC的中点，若∠BAC＝104°，∠C＝40°．则有下列结论：①∠BAE＝52°；②∠DAE＝2°；③EF＝ED；④S△ABF=12S△ABC．其中正确的有（　　）
A．1个 B．2个 C．3个 D．4个
二、填空题（本大题共8小题，每小题3分，共24分）请把答案直接填写在横线上
11．（2020春?白云区期末）如图，在Rt△ABC中，∠C＝90°，AB＝16，AD平分∠BAC交BC于点D，若CD＝4，则△ABD的面积为　 　．
12．（2020秋?长春期末）如图，OC是∠AOB的角平分线，点P是OC上一点，PM⊥OB于点M，点N是射线OA上的一个动点，若PM＝7，则PN的最小值为　 　．
13．（2019秋?潘集区月考）如图所示，△ABC中∠C＝90°，AM平分∠CAB，CM＝15cm，那么M到AB的距离是　 　cm．
14．（2020春?平江县期末）如图，在△ABC中，∠C＝90°，AD平分∠BAC，AB＝8，CD＝3，则△ABD的面积是　 　．
15．（2019秋?沙河口区期末）如图，在△ABC中，∠ABC，∠ACB的角平分线交于点O，连接AO并延长交BC于D，OH⊥BC于H，若∠BAC＝60°，OH＝5，则OA＝　 　．
16．（2019秋?南宁期末）如图，在Rt△ABC中，∠C＝90°，∠BAC的平分线AD交BC于点D，若CD＝3，AB＝8，则△ABD的面积是　 　．
17．（2019秋?河南期末）如图，已知△ABC的周长是20，OB，OC分别平分∠ABC和∠ACB，OD⊥BC于点D，且OD＝2，△ABC的面积是　 　．
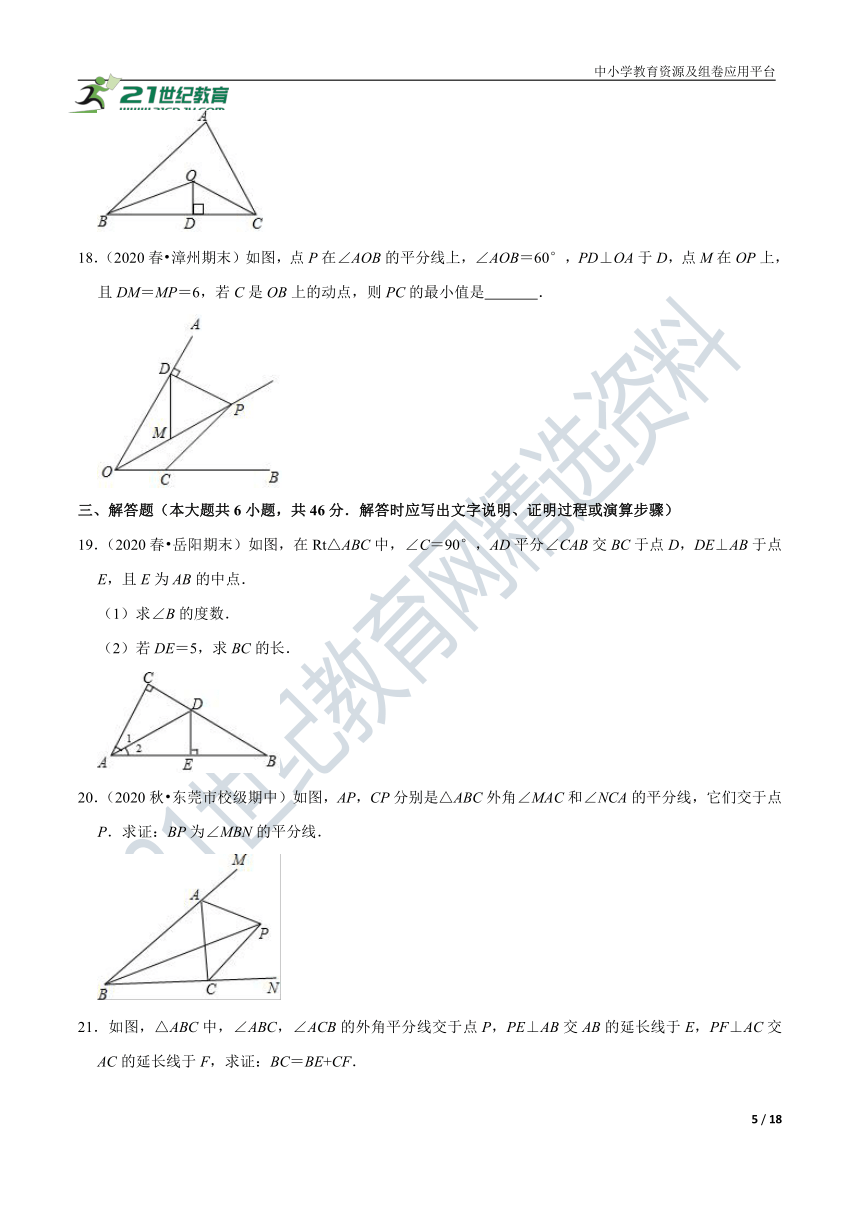
18．（2020春?漳州期末）如图，点P在∠AOB的平分线上，∠AOB＝60°，PD⊥OA于D，点M在OP上，且DM＝MP＝6，若C是OB上的动点，则PC的最小值是　 　．
三、解答题（本大题共6小题，共46分．解答时应写出文字说明、证明过程或演算步骤）
19．（2020春?岳阳期末）如图，在Rt△ABC中，∠C＝90°，AD平分∠CAB交BC于点D，DE⊥AB于点E，且E为AB的中点．
（1）求∠B的度数．
（2）若DE＝5，求BC的长．
20．（2020秋?东莞市校级期中）如图，AP，CP分别是△ABC外角∠MAC和∠NCA的平分线，它们交于点P．求证：BP为∠MBN的平分线．
21．如图，△ABC中，∠ABC，∠ACB的外角平分线交于点P，PE⊥AB交AB的延长线于E，PF⊥AC交AC的延长线于F，求证：BC＝BE+CF．
22．（2019秋?交城县期末）已知：如图，在Rt△ABC中，∠ACB＝90°，∠B＝60°，AD，CE是角平分线，AD与CE相交于点F，FM⊥AB，FN⊥BC，垂足分别为M，N．求证：FE＝FD．
23．（2019秋?涡阳县期末）已知：如图，△ABC的角平分线BE、CF相交于点P．求证：点P在∠A的平分线上．
24．（2019秋?高邮市期末）如图，△ABC中，∠ACB＝90°，AB＝10cm，BC＝6cm，若点P从点A出发以每秒1cm的速度向点C运动，设运动时间为t秒（t＞0）．
（1）若点P恰好在∠ABC的角平分线上，求出此时t的值；
（2）若点P使得PB+PC＝AC时，求出此时t的值．
答案
一、选择题（本大题共10小题，每小题3分，共30分）在每小题所给出的四个选项中，只有一项是符合题目要求的．
1．【解析】作PQ′⊥OM于Q′，
∵∠MON＝60°，OP平分∠MON，
∴∠POQ′＝30°，
∴PQ′=12OP＝2，
由垂线段最短可知，PQ的最小值是2，
故选：B．
2．【解析】过P点作PH⊥OB于H，如图，
∵OP平分∠AOB，PD⊥OA，PH⊥OB于H，
∴PH＝PD＝3，
∵点E是射线OB上的一个动点，
∴点E与H点重合时，PE有最小值，最小值为3．
故选：A．
3．【解析】∵AB＝4，△ABE的面积为12，
∴点E到直线AB的距离=2×124=6，
∵E为∠BAC平分线AP上一点，
∴点E到直线AC的距离＝6，
故选：D．
4．【解析】如图，
∵CD：BD＝3：4．
设CD＝3x，则BD＝4x，
∴BC＝CD+BD＝7x，
∵BC＝21，
∴7x＝21，
∴x＝3，
∴CD＝9，
过点D作DE⊥AB于E，
∵AD是∠BAC的平分线，∠C＝90°，
∴DE＝CD＝9，
∴点D到AB边的距离是9，
故选：B．
5．【解析】当DP⊥BC时，DP的长最小，
∵BD⊥CD，
∴∠BDC＝90°，
∵∠A＝90°，∠ADB＝∠C，∠A+∠ADB+∠ABD＝180°，∠BDC+∠C+∠CBD＝180°，
∴∠ABD＝∠CBD，
∵∠A＝90°，
∴当DP⊥BC时，DP＝AD，
∵AD＝4，
∴DP的最小值是4，
故选：A．
6．【解析】作DE⊥OB于E，如图，
∵OC是∠AOB的角平分线，DP⊥OA，DE⊥OB，
∴DE＝DP＝4，
∴S△ODQ=12×3×4＝6．
故选：D．
7．【解析】∵BE是AC边的中线，
∴AE＝CE，
∵△ABE的面积=12×AE×AB，△BCE的面积=12×CE×AB，
∴△ABE的面积＝△BCE的面积，故①正确；
∵AD是BC边上的高，
∴∠ADC＝90°，
∵∠BAC＝90°，
∴∠DAC+∠ACB＝90°，∠FAG+∠DAC＝90°，
∴∠FAG＝∠ACB，
∵CF是∠ACB的角平分线，
∴∠ACF＝∠FCB，∠ACB＝2∠FCB，
∴∠FAG＝2∠FCB，故②错误；
∵在△ACF和△DGC中，∠BAC＝∠ADC＝90°，∠ACF＝∠FCB，
∴∠AFG＝180°﹣∠BAC﹣∠ACF，∠AGF＝∠DGC＝180°﹣∠ADC﹣∠FCB，
∴∠AFG＝∠AGF，
∴AF＝AG，故③正确；
根据已知不能推出∠HBC＝∠HCB，即不能推出HB＝HC，故④错误；
即正确的为①③，
故选：D．
8．【解析】由作法得DE是AB的垂直平分线，
∴AD＝BD，AE＝BE，故A、C选项正确；
∵EA＝EB，
∴∠A＝∠ABE，
∴∠BEC＝∠A+∠ABE＝2∠DBE，故B选项正确；
故选：D．
9．【解析】∵BE平分∠ABC，∠ACB＝90°，DE⊥AB于点D，
∴DE＝EC，
∵AE+DE＝3（cm），
∴AE+EC＝3（cm），
即：AC＝3cm，
故选：B．
10．【解析】AE是△ABC的角平分线，∠BAC＝104°，
∴∠BAE＝∠CAE＝52°，
∴①正确；
∵∠C＝40°，AD⊥BC，
∴∠CAD＝50°，
∴∠DAE＝∠CAE﹣∠CAD＝52°﹣50°＝2°，
∴②正确；
∵没有条件能证得EF＝DE，
∴EF不一定等于ED，
∴③错误；
∵点F为BC的中点，
∴BF=12BC，
∴S△ABF=12S△ABC，
∴④正确；
故选：C．
二、填空题（本大题共8小题，每小题3分，共24分）请把答案直接填写在横线上
11．【解析】作DE⊥AB于E，
∵AD平分∠BAC，∠C＝90°，DE⊥AB，
∴DE＝DC＝4，
∴△ABD的面积=12×AB×DE＝32，
故答案为：32．
12．【解析】过P作PN'作OA于N'，
当PN⊥OA时，PN的值最小，
则PN＝PN'，
∵OC平分∠AOB，PM⊥OB，
∴PM＝PN'，
∵PM＝7，
∴PN'＝7，
∴PN的最小值为7，
故答案为：7．
13．【解析】如图，过点M作DM⊥AB于D，
∵∠C＝90°，AM是∠CAB的平分线，
∴DM＝CM＝15cm，
即M到AB的距离为15cm．
故答案为：15．
14．【解析】作DE⊥AB于E，如图，
∵AD平分∠BAC，DE⊥AB，DC⊥AC，
∴DE＝DC＝3，
∴S△ABD=12×8×3＝12．
故答案为12．
15．【解析】作OE⊥AB交AB于E，
∵OB平分∠ABC，OH⊥BC，
∴OE＝OH＝5，
∵∠ABC，∠ACB的角平分线交于点O，
∴AO平分∠BAC，
∵∠BAC＝60°，
∴∠BAO＝30°，
∴AO＝2OE＝10，
故答案为：10．
16．【解析】作DE⊥AB于E，
∵AD为角∠BAC平分线，∠C＝90°，DE⊥AB，
∴DE＝DC＝3，
∴△ABD的面积=12×AB×DE=12×8×3＝12，
故答案为：12．
17．【解析】如图，连接OA，过O作OE⊥AB于E，OF⊥AC于F，
∵OB、OC分别平分∠ABC和∠ACB，
∴OE＝OF＝OD＝2，
∵△ABC的周长是20，OD⊥BC于D，且OD＝2，
∴S△ABC=12×AB×OE+12×BC×OD+12×AC×OF
=12×（AB+BC+AC）×2
=12×20×2
＝20，
故答案为：20．
18．【解析】∵P是∠AOB角平分线上的一点，∠AOB＝60°，
∴∠AOP=12∠AOB＝30°，
∴∠DPO＝60°，
∵PM＝DM＝6，
∴∠MDP＝∠DPM＝60°，
∵∠PDO＝90°，
∴∠ODM＝30°＝∠AOP，
∴OM＝DM＝6，
∴OP＝12，
∴PD=12OP＝6，
∵点C是OB上一个动点，
∴PC的最小值为P到OB距离，
∴PC的最小值＝PD＝6，
故答案为：6．
三、解答题（本大题共6小题，共46分．解答时应写出文字说明、证明过程或演算步骤）
19．【解析】（1）∵DE⊥AB于点E，E为AB的中点，
∴DE是线段AB的垂直平分线，
∴DA＝DB，
∴∠2＝∠B，
∵∠C＝90°，
∴∠B＝∠1＝∠2＝30°；
（2）∵DE⊥AB，∠B＝30°，
∴BD＝2DE＝10，
∵AD平分∠CAB，∠C＝90°，DE⊥AB，
∴DC＝DE＝5，
∴BC＝CD+BD＝15．
20．【解析】证明：过P作三边AB、AC、BC的垂线段PD、PE、PF，
∵AP是△ABC的外角平分线，PD⊥AD，PF⊥AC，
∴PD＝PF（角平分线上的点到角两边的距离相等），
∵CP是△ABC的外角平分线，PE⊥AC，PF⊥BC，
∴PE＝PF（角平分线上的点到角两边的距离相等），
又∵PD＝PE，PD⊥AD，PE⊥AC，
∴AP为∠MBN的平分线（在角的内部，到角两边距离相等的点在角的平分线上）．
21．【解析】证明：作PH⊥BC于H，
∵CP是∠FCB的平分线，PF⊥AC，PH⊥BC，
∴PF＝PH，
∴CF＝CH，
同理，BH＝BE，
∴BC＝CH+BH＝BE+CF．
22．【解析】证明：连接BF，
∵F是△ABC的角平分线交点，
∴BF也是角平分线，
∵FM⊥AB，FN⊥BC，
∴MF＝FN，∠DNF＝∠EMF＝90°，
∵在Rt△ABC中，∠ACB＝90°，∠ABC＝60°，
∴∠BAC＝30°，
∴∠DAC=12∠BAC＝15°，
∴∠CDA＝75°，
∵∠NFC＝45°，∠MFN＝120°，
∴∠MFE＝15°，
∴∠MEF＝75°＝∠NDF，
在△DNF和△EMF中，
∠DNF=∠EMF∠NDF=∠MEFNF=MF，
∴△DNF≌△EMF（AAS），
∴FE＝FD．
23．【解析】证明：如图，过点P作PD⊥AB、PM⊥BC、PN⊥AC垂足分别为D、M、N，
∵BE平分∠ABC，点P在BE上，
∴PD＝PM，
同理，PM＝PN，
∴PD＝PN，
∴点P在∠A的平分线上．
24．【解析】（1）作PD⊥AB于D，如图，AP＝t，
∵∠ACB＝90°，AB＝10，BC＝6，
∴AC=102-62=8，
∵BP平分∠ABC，
∴PC＝PD＝8﹣t，
∵S△ABP+S△BCP＝S△ABC，
∴12×10×（8﹣t）+12×6×（8﹣t）=12×6×8，
解得t＝5，
即此时t的值为5s；
（2）∵PB+PC＝AC，
∴PB＝PA＝t，
在Rt△BCP中，∵PC2+BC2＝BP2，
∴（8﹣t）2+62＝t2，解得t=254，
即此时t的值为254．