华师大版数学八年级上12.2立方根课件
文档属性
| 名称 | 华师大版数学八年级上12.2立方根课件 |  | |
| 格式 | rar | ||
| 文件大小 | 244.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-20 15:41:23 | ||
图片预览







文档简介
(共27张PPT)
立方根
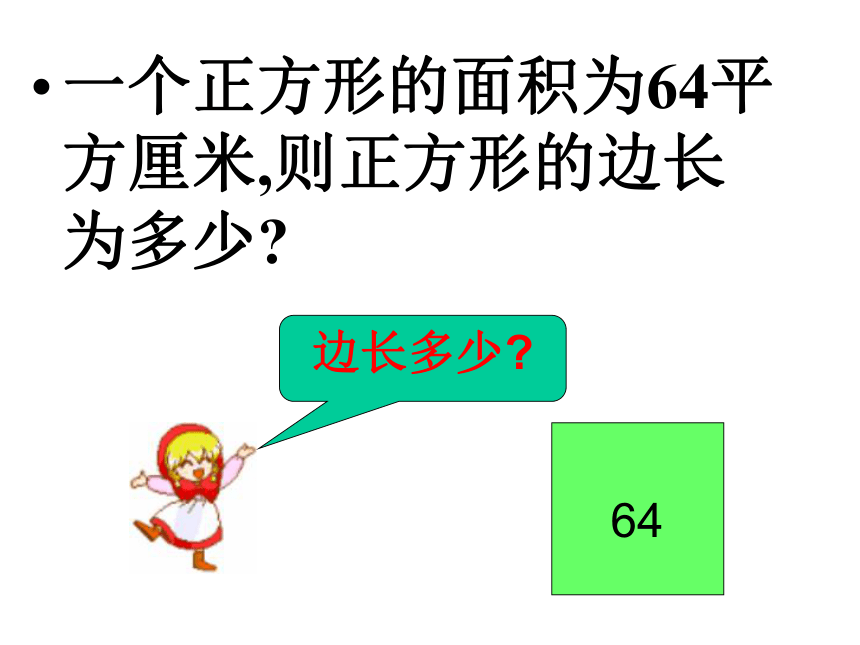
一个正方形的面积为64平方厘米,则正方形的边长为多少
边长多少
64
要做一个体积为64cm3的立方体模型(如图),它的棱要取多少长?你是怎么知道的?
什么数的立方等于-64?
由前面的学习可知:在式子 中
求括号里的数,这实际上是:
已知指数和幂求底数的运算,叫做开方运算。
我们把括号里的±3叫做9的平方根(二次方根)。
同理:若
这也是已知指数和幂求底数的运算,仍然叫做开方运算
我们把括号里的 3 叫做27的立方根(三次方根)
3
一般地,如果 ,那么 叫 的立方根,也叫做 的三次方根 , 叫 的立方数
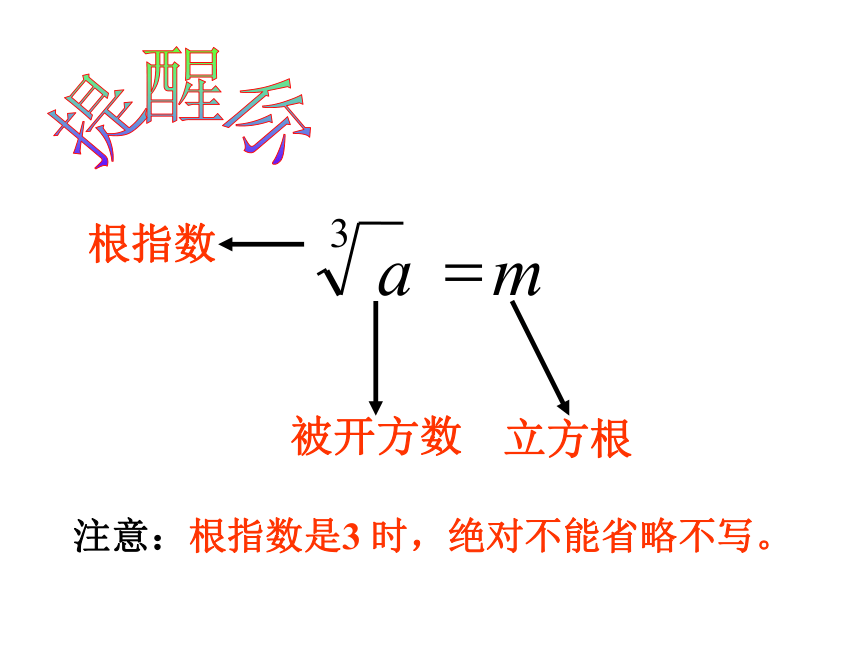
读作:“三次根号 ”,其中 叫被开方数,3 是根指数。
数 的立方根用符号 表示。
3
例如:
∵
∴ 5 是125 的立方根。
也可以说,125 的立方根是 5 。
用式子表示为:
3
注意: 的根指数 3 不能省略,要写在根
号的左上角,而且要写得小一些,不能写成
3
m
a
=
3
被开方数
立方根
根指数
注意:根指数是3 时,绝对不能省略不写。
练习:用根号表示下列各数的立方根:
(1)27;(2)-64;(3)0;
(4)-0.125;(5)
解:(1) (2) (3)
(4) (5)
求一个数的立方根(三次方根)的运算,叫做开立方,开立方运算的结果就是立方根。
因为开立方与立方互为逆运算。
所以我们可以运用立方运算来求一个数的立方根。
例1:求下列各数的立方根。
(1)-27; (2)27; (3)-0.216;
(4)0; (5)
解:
∵
∴ -27的立方根是-3。
请你仿照上面的例子完成其余几个小题。
即
3
正数有立方根吗?如果有,有几个。
负数呢?
零呢?
从上面的例1可知:一个正数有一个正的立方根;一个负数有一个负的立方根,零的立方根是零。
平方根 立方根
表示方法
被开方数
性质
平方根与立方根的区别:
非负数
任意实数
正数的平方根有两个;0的平方根是0;负数没有平方根。
正数的立方根是正数;
0的立方根是0;负数的立方根是负数
平方根:
立方根:
从上面的例题可知:
3
27
3
=
3
27
3
-
=
-
由此可得出:
3
3
27
27
-
=
-
也就是把根号里的“负号”直接从根号里面提到了根号“外面” 。
特别注意:平方根不能这样哟!
由此得出求一个负数的立方根的一般方法:
也就是说,求一个负数的立方根,可以先求出这个负数的绝对值的立方根,然后再取它的相反数。
-
=
3
a
-
3
2
8
-
=
8
(2)
3
3
-
=
-
(3)
5
.
0
125
.
0
3
-
=
-
例2:求下列各式的值。
8
3
-
解:(1)
3
(1) ;(2) ;(3)
(4) (5) (6)
3
3
3
3
3
课内练习:
1、判断下列说法是否正确,并说明理由:
(2)负数不能开立方。
3、分别求下列各式的值。
2、求1,-1, 的立方根。
(1) ;(2) , (3)
(1) 的立方根是± ;
2
3
练一练
1、判断下列说法是否正确,并说明理由:
(1)4的平方根是2; (2) — 8没有立方根;
(3)8的立方根是±2; (4) —8的立方根是—2
2、填空:
(1)∵( )3 = -125, ∴ = ;
(2)∵( )3 = , ∴ = ;
(1) (2) +
3、求下列各数的立方根
(1)0; (2)-0.027; (3) ;
(4)343
4、计算
5、判断下列说法是否正确,并说明理由:
(1)互为相反数的数的立方根也互为相反数
(2)立方根是它本身的数只有零
(3)平方根是它本身的数只有零
6、如果要制作一个立方体,使它的体积是已知立方体体积的27倍,那么它的棱长应是已知立方体的棱长的几倍?
例3. 解方程:
(1)x3=0.125; (2)3(x-4)3-1536=0.
解:(1)x3=0.125
x=0.5.
(2)3(x-4)3-1536=0
3(x-4)3=1536
(x-4)3=512
x-4=8
x=12.
大胆试一试
1、-82的立方根是_________.
2、 的立方根是_________.
3、 的整数部分是_________.
4、27的立方根与x的一个平方根相同,则x=_______.
5、一个数的平方根与它的立方根相等,则这个数是
________.
(1)下列语句正确的是( )
A. 的立方根是2 B. 是27负的立方根
C. 的立方根是 D. 的立方根是-1
(2)下列说法中错误的个数是( )
①负数没有立方根,②1的立方根与平方根都是1,③ 的平方根是 ,④
A.1个 B.2个 C.3个 D.4个
(5)某数的立方根等于这个数的算术平方根,则这个数等于( )
A.0 B. C. 或0 D.0或1
(1) 的立方根是_______.
(2) 是_____的立方根.
(3)81的平方根的立方根是_______.
(4) _______.
(5) 的立方根是______.
(6) 的立方根是________.
(7)若 ,则 _______.
(3)平方根是它本身的数只有零。
(1)互为相反数的数的立方根也互为相反数。
(2)立方根是它本身的数只有零。
讨论:
通过今天的学习,
用你自己的话说说你的收获和体会
立方根
一个正方形的面积为64平方厘米,则正方形的边长为多少
边长多少
64
要做一个体积为64cm3的立方体模型(如图),它的棱要取多少长?你是怎么知道的?
什么数的立方等于-64?
由前面的学习可知:在式子 中
求括号里的数,这实际上是:
已知指数和幂求底数的运算,叫做开方运算。
我们把括号里的±3叫做9的平方根(二次方根)。
同理:若
这也是已知指数和幂求底数的运算,仍然叫做开方运算
我们把括号里的 3 叫做27的立方根(三次方根)
3
一般地,如果 ,那么 叫 的立方根,也叫做 的三次方根 , 叫 的立方数
读作:“三次根号 ”,其中 叫被开方数,3 是根指数。
数 的立方根用符号 表示。
3
例如:
∵
∴ 5 是125 的立方根。
也可以说,125 的立方根是 5 。
用式子表示为:
3
注意: 的根指数 3 不能省略,要写在根
号的左上角,而且要写得小一些,不能写成
3
m
a
=
3
被开方数
立方根
根指数
注意:根指数是3 时,绝对不能省略不写。
练习:用根号表示下列各数的立方根:
(1)27;(2)-64;(3)0;
(4)-0.125;(5)
解:(1) (2) (3)
(4) (5)
求一个数的立方根(三次方根)的运算,叫做开立方,开立方运算的结果就是立方根。
因为开立方与立方互为逆运算。
所以我们可以运用立方运算来求一个数的立方根。
例1:求下列各数的立方根。
(1)-27; (2)27; (3)-0.216;
(4)0; (5)
解:
∵
∴ -27的立方根是-3。
请你仿照上面的例子完成其余几个小题。
即
3
正数有立方根吗?如果有,有几个。
负数呢?
零呢?
从上面的例1可知:一个正数有一个正的立方根;一个负数有一个负的立方根,零的立方根是零。
平方根 立方根
表示方法
被开方数
性质
平方根与立方根的区别:
非负数
任意实数
正数的平方根有两个;0的平方根是0;负数没有平方根。
正数的立方根是正数;
0的立方根是0;负数的立方根是负数
平方根:
立方根:
从上面的例题可知:
3
27
3
=
3
27
3
-
=
-
由此可得出:
3
3
27
27
-
=
-
也就是把根号里的“负号”直接从根号里面提到了根号“外面” 。
特别注意:平方根不能这样哟!
由此得出求一个负数的立方根的一般方法:
也就是说,求一个负数的立方根,可以先求出这个负数的绝对值的立方根,然后再取它的相反数。
-
=
3
a
-
3
2
8
-
=
8
(2)
3
3
-
=
-
(3)
5
.
0
125
.
0
3
-
=
-
例2:求下列各式的值。
8
3
-
解:(1)
3
(1) ;(2) ;(3)
(4) (5) (6)
3
3
3
3
3
课内练习:
1、判断下列说法是否正确,并说明理由:
(2)负数不能开立方。
3、分别求下列各式的值。
2、求1,-1, 的立方根。
(1) ;(2) , (3)
(1) 的立方根是± ;
2
3
练一练
1、判断下列说法是否正确,并说明理由:
(1)4的平方根是2; (2) — 8没有立方根;
(3)8的立方根是±2; (4) —8的立方根是—2
2、填空:
(1)∵( )3 = -125, ∴ = ;
(2)∵( )3 = , ∴ = ;
(1) (2) +
3、求下列各数的立方根
(1)0; (2)-0.027; (3) ;
(4)343
4、计算
5、判断下列说法是否正确,并说明理由:
(1)互为相反数的数的立方根也互为相反数
(2)立方根是它本身的数只有零
(3)平方根是它本身的数只有零
6、如果要制作一个立方体,使它的体积是已知立方体体积的27倍,那么它的棱长应是已知立方体的棱长的几倍?
例3. 解方程:
(1)x3=0.125; (2)3(x-4)3-1536=0.
解:(1)x3=0.125
x=0.5.
(2)3(x-4)3-1536=0
3(x-4)3=1536
(x-4)3=512
x-4=8
x=12.
大胆试一试
1、-82的立方根是_________.
2、 的立方根是_________.
3、 的整数部分是_________.
4、27的立方根与x的一个平方根相同,则x=_______.
5、一个数的平方根与它的立方根相等,则这个数是
________.
(1)下列语句正确的是( )
A. 的立方根是2 B. 是27负的立方根
C. 的立方根是 D. 的立方根是-1
(2)下列说法中错误的个数是( )
①负数没有立方根,②1的立方根与平方根都是1,③ 的平方根是 ,④
A.1个 B.2个 C.3个 D.4个
(5)某数的立方根等于这个数的算术平方根,则这个数等于( )
A.0 B. C. 或0 D.0或1
(1) 的立方根是_______.
(2) 是_____的立方根.
(3)81的平方根的立方根是_______.
(4) _______.
(5) 的立方根是______.
(6) 的立方根是________.
(7)若 ,则 _______.
(3)平方根是它本身的数只有零。
(1)互为相反数的数的立方根也互为相反数。
(2)立方根是它本身的数只有零。
讨论:
通过今天的学习,
用你自己的话说说你的收获和体会
