五年级上册【数学(人教版)】平行四边形的面积(第2课时) 1教学设计(表格式)
文档属性
| 名称 | 五年级上册【数学(人教版)】平行四边形的面积(第2课时) 1教学设计(表格式) |
|
|
| 格式 | zip | ||
| 文件大小 | 597.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-18 00:00:00 | ||
图片预览



文档简介
课程基本信息
课题
平行四边形的面积(第2课时)
教科书
书名:义务教育教科书数学五年级上册
出版社:人民教育出版社
出版日期:2014
年
3
月第1版
学习目标
学习目标:
1.进一步掌握平行四边形的面积计算公式,理解平行四边形的底、高与面积的关系,能灵活的利用公式解决简单的实际问题。
2.在动手操作、观察比较、分析推理中,发展空间观念,体会转化思想,提高解决问题的能力。
3.感受数学知识间的联系,体验数学学习的乐趣,养成乐于思考,勇于探究的学习品质。
学习重点:掌握平行四边形的面积计算公式,能利用公式解决实际问题。
学习难点:理解平行四边形的底、高与面积的关系。
教学过程
时间
教学
环节
主要师生活动
1分钟
一、
复习引入,回忆旧知
上节课,我们学行四边形的面积。回忆一下,平行四边形的面积怎样计算?我们是怎样推导出平行四边形的面积计算公式?
学生回忆:平行四边形的面积=底×高。
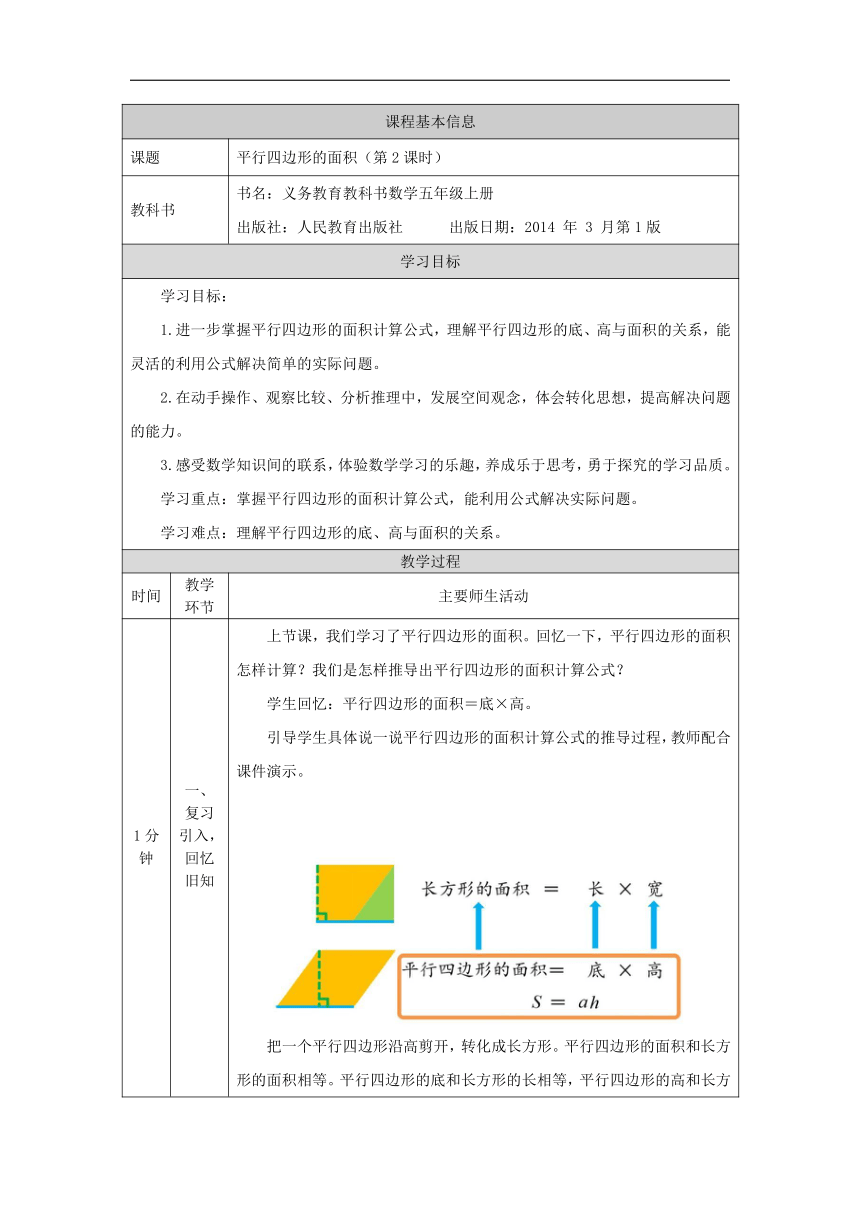
引导学生具体说一说平行四边形的面积计算公式的推导过程,教师配合课件演示。
把一个平行四边形沿高剪开,转化成长方形。平行四边形的面积和长方形的面积相等。平行四边形的底和长方形的长相等,平行四边形的高和长方形的宽相等。因为长方形的面积是长×宽,所以平行四边形的面积是底×高。
9分30秒
二、
深入研究,
理解底、高与面积的关系
(一)回顾任务,深入探究
实践活动:用纸板制作一个长18cm、宽15cm的长方形框架。推拉框架,看看有什么发现?
1.展示学生作品:
观点一:把长方形推拉成平行四边形后,周长和面积都没有变化。
观点二:把长方形推拉成平行四边形后,周长没变,面积变了。
2.深入思考,辨析底、高与面积的关系。
引导学生观察思考。
预设:因为推拉前后两条长边与两条短边的长度没有变,所以周长没有发生变化。但面积变了,因为把长方形向右拉成平行四边形后,比原来的长方形矮了。
提问:变矮了是怎么回事?拉动手中的长方形框架看一看。
学生操作后汇报:这个角变小了,高就变短了,高的长短与角的变化有关系。由于高变短了,平行四边形的面积就变小了。
提问:把原来的长方形框架与拉动后的平行四边形画下来,快看看,确实变矮了吗?面积真的变了吗?有什么办法能说明面积发生变化了。
方式一:用数据说明。
方式二:用割补法说明。
提问:继续向右拉动这个框架,周长和面积有什么变化呢?
总结:继续向右拉动这个框架,周长还是不变,面积会越来越小。因为底仍然不变,但是高逐渐变短,面积也在不断变小。
3.分析平行四边形的面积为什么不能用邻边相乘。
提问:通过刚才的活动,能说说为什么平行四边形的面积不能用邻边相乘吗?
预设一:当把长方形拉成平行四边形后,四条边的长度是不变的,如果用邻边相乘求面积,面积应该总是不变的。但在实际拉动过程中,我们看到面积变了。所以不能用邻边相乘求平行四边形的面积。
预设二:朝着一个方向拉动时,虽然底没变,但是高在变,高变的越短,面积就越小。平行四边形的面积是和底、高有关系的。所以平行四边形的面积要用底乘对应的高来求,而不能用邻边相乘。
(二)巩固应用
提问:你能想办法求出平行四边形的面积吗?
学生展示作品:
选择不同的边作底,然后找到对应高计算面积。只要底和高是相对应的,就能求出平行四边形的面积。
总结:计算平行四边形的面积时,关键是要找到对应的底和高,只有用对应的底和高相乘,才能计算出平行四边形的面积。
(三)解决问题
独立解决问题。
呈现学生作品,交流讨论。
引导学生观察比较,分析讨论谁做的对。
预设一:麦田的形状是平行四边形,都是先求出麦田的面积,250×84=21000(平方米)。求面积这一步是正确的。
预设二:小伟没换算。求每公顷的产量是多少吨,要用总吨数÷公顷数。计算出的面积是以平方米作单位的,要换算成以公顷作单位,21000平方米=2.1公顷,再用14.7÷2.1=7(吨)。芳芳的做法正确。
总结:这道题因为单位不统一,需要转化单位。在解决问题时,要认真审题,读懂每一条信息。
8分钟
三、利用公式解决简单的实际问题
(一)发现面积相等的平行四边形
下面图中两个平行四边形的面积相等吗?为什么?
学生通过计算面积和分析比较后得到结论,等底等高的平行四边形,面积相等。
(二)灵活运用计算公式解决问题
这个平行四边形的高是多少?
独立解决问题,汇报交流。
方法一:平行四边形面积÷底=高。
方法二:列方程解决问题。
(三)渗透三角形和平行四边形面积的关系
每个小方格的边长是1
cm,这个平行四边形的面积是多少?涂色的三角形的面积是多少?
学生独立思考解决问题。
汇报交流。
方法一:求出平行四边形的面积,猜测三角形的面积是平行四边形面积的一半。
方法二:数方格求出三角形的面积,验证猜想。
进一步猜测,三角形的面积和平行四边形的面积有关系。
1分钟
四、
回顾总结
(一)学生谈收获
(二)教师总结
30秒
五、
布置作业
1.数学书第89页第3题。
2.数学书第90页第7题。
课题
平行四边形的面积(第2课时)
教科书
书名:义务教育教科书数学五年级上册
出版社:人民教育出版社
出版日期:2014
年
3
月第1版
学习目标
学习目标:
1.进一步掌握平行四边形的面积计算公式,理解平行四边形的底、高与面积的关系,能灵活的利用公式解决简单的实际问题。
2.在动手操作、观察比较、分析推理中,发展空间观念,体会转化思想,提高解决问题的能力。
3.感受数学知识间的联系,体验数学学习的乐趣,养成乐于思考,勇于探究的学习品质。
学习重点:掌握平行四边形的面积计算公式,能利用公式解决实际问题。
学习难点:理解平行四边形的底、高与面积的关系。
教学过程
时间
教学
环节
主要师生活动
1分钟
一、
复习引入,回忆旧知
上节课,我们学行四边形的面积。回忆一下,平行四边形的面积怎样计算?我们是怎样推导出平行四边形的面积计算公式?
学生回忆:平行四边形的面积=底×高。
引导学生具体说一说平行四边形的面积计算公式的推导过程,教师配合课件演示。
把一个平行四边形沿高剪开,转化成长方形。平行四边形的面积和长方形的面积相等。平行四边形的底和长方形的长相等,平行四边形的高和长方形的宽相等。因为长方形的面积是长×宽,所以平行四边形的面积是底×高。
9分30秒
二、
深入研究,
理解底、高与面积的关系
(一)回顾任务,深入探究
实践活动:用纸板制作一个长18cm、宽15cm的长方形框架。推拉框架,看看有什么发现?
1.展示学生作品:
观点一:把长方形推拉成平行四边形后,周长和面积都没有变化。
观点二:把长方形推拉成平行四边形后,周长没变,面积变了。
2.深入思考,辨析底、高与面积的关系。
引导学生观察思考。
预设:因为推拉前后两条长边与两条短边的长度没有变,所以周长没有发生变化。但面积变了,因为把长方形向右拉成平行四边形后,比原来的长方形矮了。
提问:变矮了是怎么回事?拉动手中的长方形框架看一看。
学生操作后汇报:这个角变小了,高就变短了,高的长短与角的变化有关系。由于高变短了,平行四边形的面积就变小了。
提问:把原来的长方形框架与拉动后的平行四边形画下来,快看看,确实变矮了吗?面积真的变了吗?有什么办法能说明面积发生变化了。
方式一:用数据说明。
方式二:用割补法说明。
提问:继续向右拉动这个框架,周长和面积有什么变化呢?
总结:继续向右拉动这个框架,周长还是不变,面积会越来越小。因为底仍然不变,但是高逐渐变短,面积也在不断变小。
3.分析平行四边形的面积为什么不能用邻边相乘。
提问:通过刚才的活动,能说说为什么平行四边形的面积不能用邻边相乘吗?
预设一:当把长方形拉成平行四边形后,四条边的长度是不变的,如果用邻边相乘求面积,面积应该总是不变的。但在实际拉动过程中,我们看到面积变了。所以不能用邻边相乘求平行四边形的面积。
预设二:朝着一个方向拉动时,虽然底没变,但是高在变,高变的越短,面积就越小。平行四边形的面积是和底、高有关系的。所以平行四边形的面积要用底乘对应的高来求,而不能用邻边相乘。
(二)巩固应用
提问:你能想办法求出平行四边形的面积吗?
学生展示作品:
选择不同的边作底,然后找到对应高计算面积。只要底和高是相对应的,就能求出平行四边形的面积。
总结:计算平行四边形的面积时,关键是要找到对应的底和高,只有用对应的底和高相乘,才能计算出平行四边形的面积。
(三)解决问题
独立解决问题。
呈现学生作品,交流讨论。
引导学生观察比较,分析讨论谁做的对。
预设一:麦田的形状是平行四边形,都是先求出麦田的面积,250×84=21000(平方米)。求面积这一步是正确的。
预设二:小伟没换算。求每公顷的产量是多少吨,要用总吨数÷公顷数。计算出的面积是以平方米作单位的,要换算成以公顷作单位,21000平方米=2.1公顷,再用14.7÷2.1=7(吨)。芳芳的做法正确。
总结:这道题因为单位不统一,需要转化单位。在解决问题时,要认真审题,读懂每一条信息。
8分钟
三、利用公式解决简单的实际问题
(一)发现面积相等的平行四边形
下面图中两个平行四边形的面积相等吗?为什么?
学生通过计算面积和分析比较后得到结论,等底等高的平行四边形,面积相等。
(二)灵活运用计算公式解决问题
这个平行四边形的高是多少?
独立解决问题,汇报交流。
方法一:平行四边形面积÷底=高。
方法二:列方程解决问题。
(三)渗透三角形和平行四边形面积的关系
每个小方格的边长是1
cm,这个平行四边形的面积是多少?涂色的三角形的面积是多少?
学生独立思考解决问题。
汇报交流。
方法一:求出平行四边形的面积,猜测三角形的面积是平行四边形面积的一半。
方法二:数方格求出三角形的面积,验证猜想。
进一步猜测,三角形的面积和平行四边形的面积有关系。
1分钟
四、
回顾总结
(一)学生谈收获
(二)教师总结
30秒
五、
布置作业
1.数学书第89页第3题。
2.数学书第90页第7题。
