2020—2021学年人教版七年级下册数学学案:5.1.3同位角 内错角 同旁内角(无答案)
文档属性
| 名称 | 2020—2021学年人教版七年级下册数学学案:5.1.3同位角 内错角 同旁内角(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 32.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-18 17:01:18 | ||
图片预览

文档简介
5.1.3
同位角
内错角
同旁内角
班级__________姓名______________得分_______________等级__________
【学习目的】在具体情境中认识同位角、内错角、同旁内角.
【学习重点】准确辨认同位角、内错角、同旁内角.
【学法难点】在较复杂的图形中辩认同位角、内错角、同旁内角.
【课前小测】
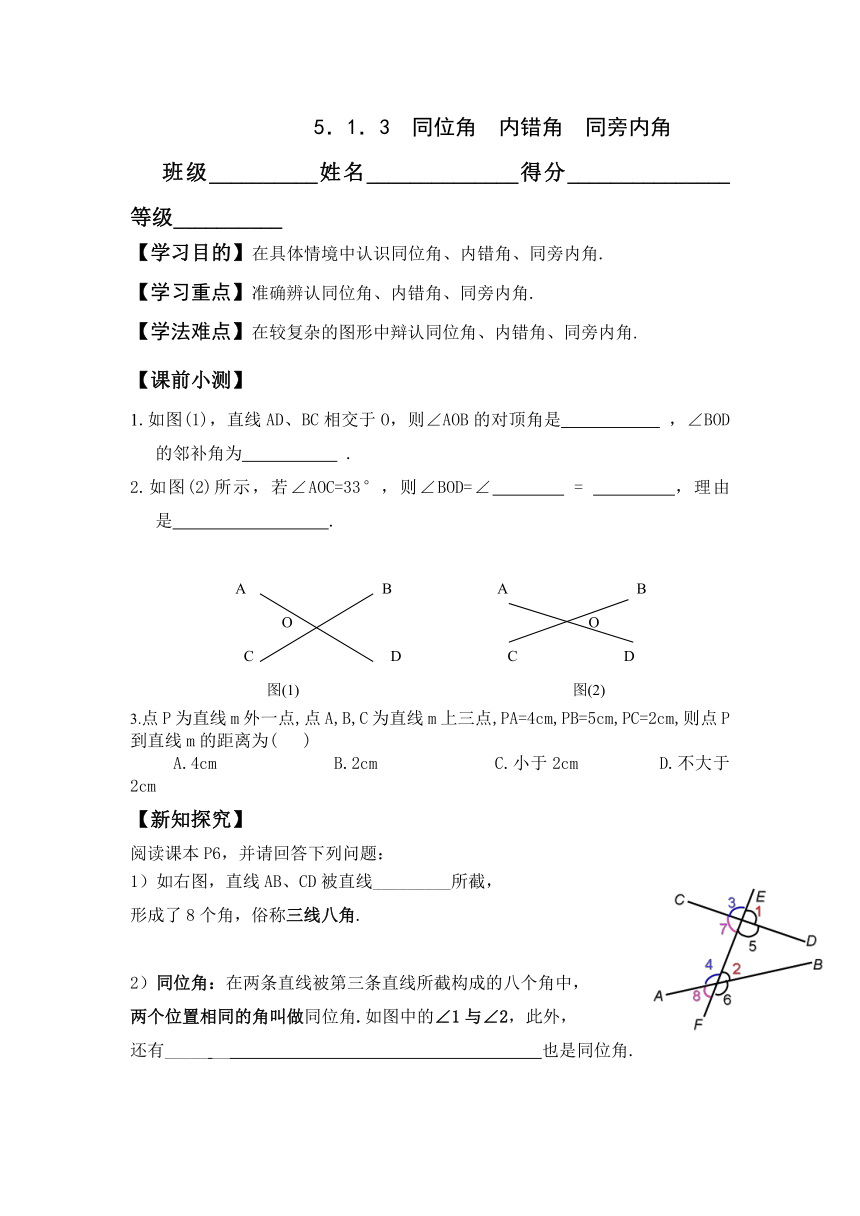
1.如图(1),直线AD、BC相交于O,则∠AOB的对顶角是
,∠BOD的邻补角为
.
2.如图(2)所示,若∠AOC=33°,则∠BOD=∠
=
,理由是
.
A
B
A
B
O
O
C
D
C
D
图(1)
图(2)
3.点P为直线m外一点,点A,B,C为直线m上三点,PA=4cm,PB=5cm,PC=2cm,则点P到直线m的距离为(
)
A.4cm
B.2cm
C.小于2cm
D.不大于2cm
【新知探究】
阅读课本P6,并请回答下列问题:
1)如右图,直线AB、CD被直线_________所截,
形成了8个角,俗称三线八角.
2)同位角:在两条直线被第三条直线所截构成的八个角中,
两个位置相同的角叫做同位角.如图中的∠1与∠2,此外,
还有_____
__
也是同位角.
3)内错角:两条直线被第三条直线所截构成的八个角中,位于两条直线的内部,且在第三条直线的两侧的两个角,叫做内错角.如图中的∠2与∠7,此外,还有__________
__
________
也是内错角.
4)同旁内角:两条直线被第三条直线所截构成的八个角中,位于两条直线的内部,且在第三条直线的同旁的两个角,叫做同旁内角.
如图中的∠2与∠5,此外,还有_____
__
_________________也是同旁内角.
注意:(1)上述的三类位置关系的角都没有公共顶点.
(2)归纳总结同位角、内错角、同旁内角的特征:
同位角:“F”
字型,“同旁同侧”
“三线八角”
内错角:“Z”
字型,“之间两侧”
同旁内角:“U”
字型,“之间同侧”
【例题解析】
例1:在右图中找出满足下列各个条件的角.
同位角:
内错角:
同旁内角:
例2:如图,直线DE交∠ABC的边BA于点F.
1)∠1和∠2是
,
∠1和∠3是
,
∠1和∠4是
。
2)如果∠1=∠4,那么∠1与∠2相等吗?
∠1与∠3互补吗?为什么?
同位角
内错角
同旁内角
班级__________姓名______________得分_______________等级__________
【学习目的】在具体情境中认识同位角、内错角、同旁内角.
【学习重点】准确辨认同位角、内错角、同旁内角.
【学法难点】在较复杂的图形中辩认同位角、内错角、同旁内角.
【课前小测】
1.如图(1),直线AD、BC相交于O,则∠AOB的对顶角是
,∠BOD的邻补角为
.
2.如图(2)所示,若∠AOC=33°,则∠BOD=∠
=
,理由是
.
A
B
A
B
O
O
C
D
C
D
图(1)
图(2)
3.点P为直线m外一点,点A,B,C为直线m上三点,PA=4cm,PB=5cm,PC=2cm,则点P到直线m的距离为(
)
A.4cm
B.2cm
C.小于2cm
D.不大于2cm
【新知探究】
阅读课本P6,并请回答下列问题:
1)如右图,直线AB、CD被直线_________所截,
形成了8个角,俗称三线八角.
2)同位角:在两条直线被第三条直线所截构成的八个角中,
两个位置相同的角叫做同位角.如图中的∠1与∠2,此外,
还有_____
__
也是同位角.
3)内错角:两条直线被第三条直线所截构成的八个角中,位于两条直线的内部,且在第三条直线的两侧的两个角,叫做内错角.如图中的∠2与∠7,此外,还有__________
__
________
也是内错角.
4)同旁内角:两条直线被第三条直线所截构成的八个角中,位于两条直线的内部,且在第三条直线的同旁的两个角,叫做同旁内角.
如图中的∠2与∠5,此外,还有_____
__
_________________也是同旁内角.
注意:(1)上述的三类位置关系的角都没有公共顶点.
(2)归纳总结同位角、内错角、同旁内角的特征:
同位角:“F”
字型,“同旁同侧”
“三线八角”
内错角:“Z”
字型,“之间两侧”
同旁内角:“U”
字型,“之间同侧”
【例题解析】
例1:在右图中找出满足下列各个条件的角.
同位角:
内错角:
同旁内角:
例2:如图,直线DE交∠ABC的边BA于点F.
1)∠1和∠2是
,
∠1和∠3是
,
∠1和∠4是
。
2)如果∠1=∠4,那么∠1与∠2相等吗?
∠1与∠3互补吗?为什么?
