2020-2021学年度 人教版七年级数学下册 5.3.1 平行线的性质 同步练习(word版含答案)
文档属性
| 名称 | 2020-2021学年度 人教版七年级数学下册 5.3.1 平行线的性质 同步练习(word版含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 154.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-18 00:00:00 | ||
图片预览


文档简介
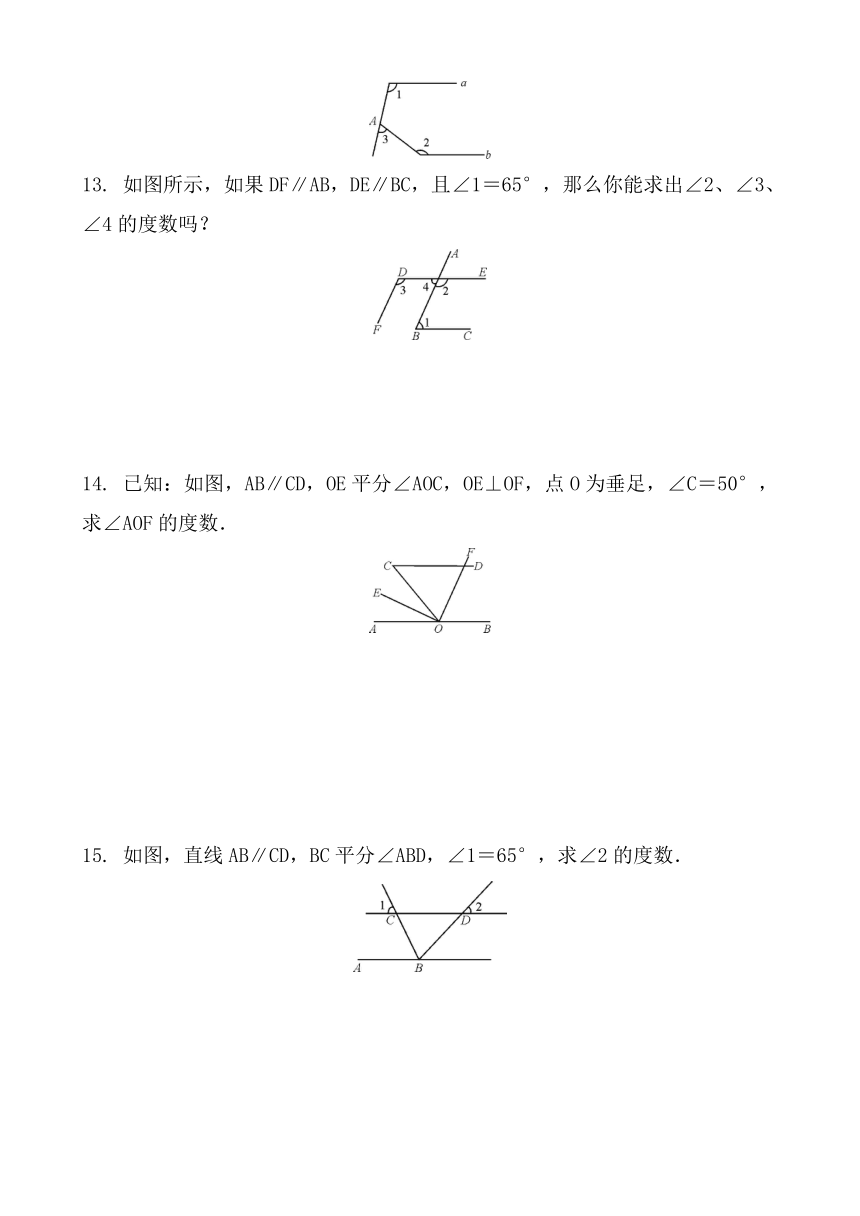
第五章 相交线与平行线 5.3.1.1 平行线的性质
1.如图直线a∥b,∠1=60°,则∠2等于( )
A.30° B.60° C.45° D.120°
2. 如图,DE∥AB,若∠ACD=55°,则∠A等于( )
A.35° B.55° C.65° D.125°
3. 如图,直线l1∥l2,直角三角板的直角顶点C在直线l1上,一锐角顶点B在直线l2上,若∠1=35°,则∠2的度数是( )
A.65° B.55° C.45° D.35°
4. 如图,一条“U”形水管中AB∥CD,若∠B=75°,则∠C等于( )
A.75° B.95° C.105° D.125°
5. 如图,平行线AB、CD被直线AE所截,∠1=80°,则∠2的度数是( )
A.80° B.90° C.100° D.110°
6. 如图,已知BD∥AC,BE平分∠ABD交AC于点E,若∠A=50°,则∠1的度数为( )
A.65° B.60° C.55° D.50°
7下列图形中,由AB∥CD,能得到∠1=∠2的是( )
8.如图,已知AB∥CD∥EF,且AF∥CG,则图中与∠A(本身不算)相等的角有( )
A.1个 B.2个 C.3个 D.4个
9. 如图,点D在∠AOB的平分线OC上,点E在OA上,ED∥OB,∠1=25°,则∠AED的度数为 .
10. 如图,AB∥CD∥EF,AC∥DF,若∠BAC=120°,则∠CDF= .
11. 如图,AB∥CD,点E在AB上,点F在CD上,如果∠CFE∶∠EFB=3∶4,∠ABF=40°,那么∠BEF的度数为 .
12.如图,a∥b,∠1=105°,∠2=140°,则∠3的度数是 .
13. 如图所示,如果DF∥AB,DE∥BC,且∠1=65°,那么你能求出∠2、∠3、∠4的度数吗?
14. 已知:如图,AB∥CD,OE平分∠AOC,OE⊥OF,点O为垂足,∠C=50°,求∠AOF的度数.
15. 如图,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数.
16. 如图,AB∥CD,点E是CD上一点,∠AEC=42°,EF平分∠AED交AB于点F,求∠AFE的度数.
17. 如图,已知直线l1∥l2,且l3与l1、l2分别交于A、B两点,点P在AB上.
(1)试找出∠1、∠2、∠3之间的关系并说明理由;
(2)如果点P在A、B两点之间运动时,问∠1、∠2、∠3之间的关系是否发生变化?
(3)如果点P在A、B两点外侧运动时,试探究∠1、∠2、∠3之间的关系(点P和A、B不重合).
答案:
1---8 BBBCC ABD
9. 50°
10. 60°
11. 60°
12. 65°
13. 解: ∵DE∥BC(已知),∴∠4=∠1(两直线平行,内错角相等),
∠1+∠2=180°(两直线平行,同旁内角互补).
∵∠1=65°(已知),∴∠4=65°(等量代换),
∠2=180°-∠1=180°-65°=115°(等式的性质),
又∵DF∥AB(已知),∴∠3=∠2=115°(两直线平行,同位角相等).
14. 解: ∵AB∥CD(已知),
∴∠AOC=∠C(两直线平行,内错角相等).
又∵∠C=50°(已知),
∴∠AOC=50°.
∵OE平分∠AOC(已知),
∴∠AOE=∠AOC=×50°=25°.又∵OE⊥OF(已知),
∴∠EOF=90°(垂直的定义).
∴∠AOF=∠AOE+∠EOF=25°+90°=115°.
15. 解:∵AB∥CD,∴∠ABC=∠1=65°,∠ABD+∠BDC=180°,
∵BC平分∠ABD,∴∠ABD=2∠ABC=130°,∴∠BDC=180°-∠ABD=50°,∴∠2=∠BDC=50°.
16. 解:∵∠AEC=42°,∴∠AED=180°-∠AEC=138°,∵EF平分∠AED,∴∠DEF=∠AED=69°,又∵AB∥CD,∴∠AFE=∠DEF=69°.
17. 解:(1)∠1+∠2=∠3.理由:如图,过点P作l1的平行线PQ.∵l1∥l2,∴l1∥l2∥PQ,∴∠1=∠4,∠2=∠5.∵∠4+∠5=∠3,∴∠1+∠2=∠3;
(2)∠1+∠2=∠3不变;
(3)∠1-∠2=∠3或∠2-∠1=∠3.理由:
①当点P在下侧时,过点P作l1的平行线PQ.∵l1∥l2,∴l1∥l2∥PQ,∴∠2=∠4,∠1=∠3+∠4,∴∠1-∠2=∠3.②当点P在上侧时,同理可得∠2-∠1=∠3.
1.如图直线a∥b,∠1=60°,则∠2等于( )
A.30° B.60° C.45° D.120°
2. 如图,DE∥AB,若∠ACD=55°,则∠A等于( )
A.35° B.55° C.65° D.125°
3. 如图,直线l1∥l2,直角三角板的直角顶点C在直线l1上,一锐角顶点B在直线l2上,若∠1=35°,则∠2的度数是( )
A.65° B.55° C.45° D.35°
4. 如图,一条“U”形水管中AB∥CD,若∠B=75°,则∠C等于( )
A.75° B.95° C.105° D.125°
5. 如图,平行线AB、CD被直线AE所截,∠1=80°,则∠2的度数是( )
A.80° B.90° C.100° D.110°
6. 如图,已知BD∥AC,BE平分∠ABD交AC于点E,若∠A=50°,则∠1的度数为( )
A.65° B.60° C.55° D.50°
7下列图形中,由AB∥CD,能得到∠1=∠2的是( )
8.如图,已知AB∥CD∥EF,且AF∥CG,则图中与∠A(本身不算)相等的角有( )
A.1个 B.2个 C.3个 D.4个
9. 如图,点D在∠AOB的平分线OC上,点E在OA上,ED∥OB,∠1=25°,则∠AED的度数为 .
10. 如图,AB∥CD∥EF,AC∥DF,若∠BAC=120°,则∠CDF= .
11. 如图,AB∥CD,点E在AB上,点F在CD上,如果∠CFE∶∠EFB=3∶4,∠ABF=40°,那么∠BEF的度数为 .
12.如图,a∥b,∠1=105°,∠2=140°,则∠3的度数是 .
13. 如图所示,如果DF∥AB,DE∥BC,且∠1=65°,那么你能求出∠2、∠3、∠4的度数吗?
14. 已知:如图,AB∥CD,OE平分∠AOC,OE⊥OF,点O为垂足,∠C=50°,求∠AOF的度数.
15. 如图,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数.
16. 如图,AB∥CD,点E是CD上一点,∠AEC=42°,EF平分∠AED交AB于点F,求∠AFE的度数.
17. 如图,已知直线l1∥l2,且l3与l1、l2分别交于A、B两点,点P在AB上.
(1)试找出∠1、∠2、∠3之间的关系并说明理由;
(2)如果点P在A、B两点之间运动时,问∠1、∠2、∠3之间的关系是否发生变化?
(3)如果点P在A、B两点外侧运动时,试探究∠1、∠2、∠3之间的关系(点P和A、B不重合).
答案:
1---8 BBBCC ABD
9. 50°
10. 60°
11. 60°
12. 65°
13. 解: ∵DE∥BC(已知),∴∠4=∠1(两直线平行,内错角相等),
∠1+∠2=180°(两直线平行,同旁内角互补).
∵∠1=65°(已知),∴∠4=65°(等量代换),
∠2=180°-∠1=180°-65°=115°(等式的性质),
又∵DF∥AB(已知),∴∠3=∠2=115°(两直线平行,同位角相等).
14. 解: ∵AB∥CD(已知),
∴∠AOC=∠C(两直线平行,内错角相等).
又∵∠C=50°(已知),
∴∠AOC=50°.
∵OE平分∠AOC(已知),
∴∠AOE=∠AOC=×50°=25°.又∵OE⊥OF(已知),
∴∠EOF=90°(垂直的定义).
∴∠AOF=∠AOE+∠EOF=25°+90°=115°.
15. 解:∵AB∥CD,∴∠ABC=∠1=65°,∠ABD+∠BDC=180°,
∵BC平分∠ABD,∴∠ABD=2∠ABC=130°,∴∠BDC=180°-∠ABD=50°,∴∠2=∠BDC=50°.
16. 解:∵∠AEC=42°,∴∠AED=180°-∠AEC=138°,∵EF平分∠AED,∴∠DEF=∠AED=69°,又∵AB∥CD,∴∠AFE=∠DEF=69°.
17. 解:(1)∠1+∠2=∠3.理由:如图,过点P作l1的平行线PQ.∵l1∥l2,∴l1∥l2∥PQ,∴∠1=∠4,∠2=∠5.∵∠4+∠5=∠3,∴∠1+∠2=∠3;
(2)∠1+∠2=∠3不变;
(3)∠1-∠2=∠3或∠2-∠1=∠3.理由:
①当点P在下侧时,过点P作l1的平行线PQ.∵l1∥l2,∴l1∥l2∥PQ,∴∠2=∠4,∠1=∠3+∠4,∴∠1-∠2=∠3.②当点P在上侧时,同理可得∠2-∠1=∠3.
