19.2.2一次函数(3) 课件(共26张PPT)
文档属性
| 名称 | 19.2.2一次函数(3) 课件(共26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-14 00:00:00 | ||
图片预览








文档简介
(共26张PPT)
人教版
八年级数学上
19.2.2.一次函数(3)
学习目标
1.理解待定系数法的意义.
2.会用待定系数法求一次函数的解析式.(重点、难点)
3.运用一次函数解决实际问题,对分段函数有初步认识.
回顾旧知
当k>0时,直线y=kx+b由左到右逐渐上升,y随x的增大而增大.
当k<0时,直线y=kx+b由左到右逐渐下降,y随x的增大而减小.
①
b>0时,直线经过第
一、二、四象限;
②
b<0时,直线经过第
二、三、四象限.
①
b>0时,直线经过第一、二、三象限;
②
b<0时,直线经过第一、三、四象限.
思考:
一次函数y=kx+b中,k,b的正负对函数图像的影响?
合作探究---待定系数法
我们学习了一次函数及其图象和性质,你能写出两个具体的一次函数解析式吗?如何画出它们的图象?
思考1:
反过来,已知一个一次函数的图象经过两个具体的点,你能求出它的解析式吗?
两点法——两点确定一条直线
合作探究---待定系数法
例1:已知一次函数的图象经过(3,5),(-4,-9)两点.
怎样确定这个一次函数的解析式呢?
分析:因为一次函数的一般形式是y=kx+b(k,b为常数,k≠0),要求出一次函数的解析式,关键是要确定k和b的值(即待定系数).
函数解析式
y=kx+b
满足条件的两点
(x1,y1),(x2,y2)
选取
解出k、b
合作探究---待定系数法
解:设这个一次函数解析式为y=kx+b
(k≠0),
将(3,5)
和(-4,-9)两点坐标代入该式中,得到一
个关于k,b的二元一次方程组:
3k
+b
=5,
-4k
+
b
=
-9,
{
{
解这个方程组,得
k=2,
b=-1.
∴这个一次函数的解析式为y
=
2x-
1.
合作探究---待定系数法
像这样,通过先设定函数解析式(确定函数模型),再根据条件确定解析式中的未知系数,从而求出函数解析式的方法称为待定系数法.
小试牛刀
1、若一次函数的图象经过点
A(2,0)且与直线y=-x+3平行,求其解析式.
解:设这个一次函数的解析式为y=kx+b.
k
=
-1,
2k
+
b
=
0,
{
由题意得
k
=
-1,
b
=
2.
{
解得
∴y=-x+2.
小试牛刀
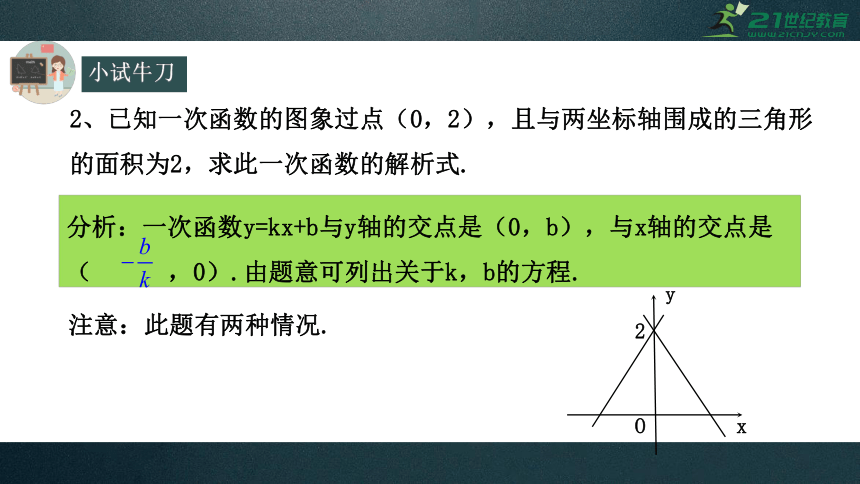
2、已知一次函数的图象过点(0,2),且与两坐标轴围成的三角形的面积为2,求此一次函数的解析式.
分析:一次函数y=kx+b与y轴的交点是(0,b),与x轴的交点是(
,0).由题意可列出关于k,b的方程.
y
x
O
2
注意:此题有两种情况.
小试牛刀
解:设一次函数的解析式为y=kx+b(k≠0)
∵一次函数y=kx+b的图象过点(0,2),
∴b=2
∵一次函数的图象与x轴的交点是(
,0),则
解得k=1或-1.
故此一次函数的解析式为y=x+2或y=-x+2.
典例精析
购买种子
数量/kg
0.5
1
1.5
2
2.5
3
3.5
4
…
付款金额/元
…
例2:“黄金1号”玉米种子的价格为5
元/kg,如果一次购买2
kg
以上的种子,超过2
kg
部分的种子的价格打8
折.
(1)填写下表:
2.5
5
7.5
10
12
14
16
18
典例精析
(2)写出购买量关于付款金额的函数解析式,并画出函数图象.
分析:从题目可知,种子的价格与
有关.
若购买种子量为x>2时,种子价格y为:
.
若购买种子量为0≤x≤2时,种子价格y为:
.
购买种子量
y=5x
y=4(x-2)+10=4x+2
典例精析
解:设购买量为x千克,付款金额为y元.
当x>2时,y=4(x-2)+10=4x+2.
当0≤x≤2时,y=5x;
(2)写出购买量关于付款金额的函数解析式,并画出函数图象.
叫做分段函数.注意:1.它是一个函数;2.要写明自变量取值范围.
y
=
5x(0≤x≤2)
4x+2(x>2)
{
y=5x(0≤x≤2)
y=4x+2(x>2)
y
x
O
1
2
10
3
14
典例精析
思考2:你能由上面的函数解析式或函数图象解决以下问题吗?
(1)一次购买1.5
kg
种子,需付款多少元?
(2)30元最多能购买多少种子?
解:(1)当0≤x≤2时,y=5x;
∴一次购买1.5
kg
种子,需付款5
×1.5=7.5元
(2)
∵
2
×5=10
<
30;
∴30元购买的种子超过2
kg
当x>2时,y=4x+2.
∴
4x+2=30,x=7
∴
30元最多能购买7
kg种子
小试牛刀
1、为节约用水,某市制定以下用水收费标准,每户每月用水不超过8立方米,每立方米收取1元外加0.3元的污水处理费;超过时,超过部分每立方米收取1.5元外加1.2元污水处理费,现设一户每月用水x立方米,应缴水费y元.
(1)求出y关于x的函数解析式;
解:y关于x的函数解析式为:
(1+0.3)x
=1.3x,
(0≤x≤8)
(1.5+1.2)(x-8)+1.3×8=2.7x-11.2.
(x>8)
y=
小试牛刀
(2)当x=10时,y=2.7×10-11.2=15.8.
(3)∵1.3×8=10.4<26.6,∴该用户用水量超过8立方米.
∴2.7x-11.2=26.6,解得x=14.
答:应缴水费为15.8元.
答:该户这月用水量为14立方米.
(2)该市一户某月若用水x=10立方米时,求应缴水费;
(3)该市一户某月缴水费26.6元,求该户这月用水量.
综合演练
1、正比例函数y=k1x与一次函数y=k2x+b的图象如图所示,它们的交点A的坐标为(3,4),并且OB=5.
(1)你能求出这两个函数的解析式吗?
(2)△AOB的面积是多少呢?
知识点拨:由OB=5可知点B的坐标为(0,-5).y=k1x的图象过点A(3,4),y=k2x+b的图象过点A(3,4),B(0,-5),代入解方程(组)即可.
综合演练
解:(1)
OB=5可知点B的坐标为(0,-5).
∵
y=k2x+b的图象过点A(3,4)、点B
(0,-5).
∴将点A(3,4)、点B
(0,-5)分别代入解析式中得:
解得:
∴y=3x-5
∵
y=k1x的图象过点A(3,4).
∴将点A(3,4)代入解析式中得3k1=4;解得:k1=
∴y=
x
3k2+b=4
b=-5
{
k2=3
b=-5
{
综合演练
(2)∵点A(3,4)
∴点A到y轴的距离为3
∴
△AOB的面积=
×3
×OB=
综合演练
2、已知一次函数y=kx+b(k≠0)的自变量的取值范围是-
3≤x≤
6,相应函数值的范围是-
5≤y≤
-
2
,求这个函数的解析式.
知识点拨:(1)当-
3≤x≤
6时,-
5≤y≤
-
2,实质是给出了两组自变量及对应的函数值;
(2)由于不知道函数的增减性,此题需分两种情况讨论.
综合演练
当k
>
0时,一次函数y=kx+b经过(-3,-2)、(6,-5)
将点(-3,-2)、(6,-5)分别代入解析式中得:
解得:
∴y=
x-3
-3k+b=-5
6k+b=-2
{
k=
b=-4
{
由题意可知:
当k<0时,一次函数y=kx+b经过(-3,-5)、(6,-2)
将点(-3,-5)、(6,-2)分别代入解析式中得:
解得:
∴y=
x-4
-3k+b=-2
6k+b=-5
{
k=
b=-3
{
综合演练
3、某医药研究所开发了一种新药,在实际验药时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(毫克)随时间x(时)的变化情况如图所示,当成年人按规定剂量服药后.
(1)服药后______时,血液中含药量最高,
达到每毫升_______毫克,接着逐步衰弱.
(2)服药6时,血液中含药量为每毫升____毫克.
x/时
y/毫克
8
4
2
6
O
2
8
4
综合演练
(3)当x≤2时y与x之间的函数解析式是___________.
(4)当x≥2时y与x之间的函数解析式是___________.
(5)如果每毫升血液中含药量4毫克或4毫克以上时,治疗疾病最有效,那么这个有效时间是______时.
y=4x
y=-x+8
4
x/时
y/毫克
8
4
2
6
O
课堂小结
本节课你有哪些收获?
1、什么是待定系数法?
2、如何利用待定系数法求函数的解析式?
课后作业
教材99页习题19.2第6、7、11题.
https://www.21cnjy.com/help/help_extract.php
人教版
八年级数学上
19.2.2.一次函数(3)
学习目标
1.理解待定系数法的意义.
2.会用待定系数法求一次函数的解析式.(重点、难点)
3.运用一次函数解决实际问题,对分段函数有初步认识.
回顾旧知
当k>0时,直线y=kx+b由左到右逐渐上升,y随x的增大而增大.
当k<0时,直线y=kx+b由左到右逐渐下降,y随x的增大而减小.
①
b>0时,直线经过第
一、二、四象限;
②
b<0时,直线经过第
二、三、四象限.
①
b>0时,直线经过第一、二、三象限;
②
b<0时,直线经过第一、三、四象限.
思考:
一次函数y=kx+b中,k,b的正负对函数图像的影响?
合作探究---待定系数法
我们学习了一次函数及其图象和性质,你能写出两个具体的一次函数解析式吗?如何画出它们的图象?
思考1:
反过来,已知一个一次函数的图象经过两个具体的点,你能求出它的解析式吗?
两点法——两点确定一条直线
合作探究---待定系数法
例1:已知一次函数的图象经过(3,5),(-4,-9)两点.
怎样确定这个一次函数的解析式呢?
分析:因为一次函数的一般形式是y=kx+b(k,b为常数,k≠0),要求出一次函数的解析式,关键是要确定k和b的值(即待定系数).
函数解析式
y=kx+b
满足条件的两点
(x1,y1),(x2,y2)
选取
解出k、b
合作探究---待定系数法
解:设这个一次函数解析式为y=kx+b
(k≠0),
将(3,5)
和(-4,-9)两点坐标代入该式中,得到一
个关于k,b的二元一次方程组:
3k
+b
=5,
-4k
+
b
=
-9,
{
{
解这个方程组,得
k=2,
b=-1.
∴这个一次函数的解析式为y
=
2x-
1.
合作探究---待定系数法
像这样,通过先设定函数解析式(确定函数模型),再根据条件确定解析式中的未知系数,从而求出函数解析式的方法称为待定系数法.
小试牛刀
1、若一次函数的图象经过点
A(2,0)且与直线y=-x+3平行,求其解析式.
解:设这个一次函数的解析式为y=kx+b.
k
=
-1,
2k
+
b
=
0,
{
由题意得
k
=
-1,
b
=
2.
{
解得
∴y=-x+2.
小试牛刀
2、已知一次函数的图象过点(0,2),且与两坐标轴围成的三角形的面积为2,求此一次函数的解析式.
分析:一次函数y=kx+b与y轴的交点是(0,b),与x轴的交点是(
,0).由题意可列出关于k,b的方程.
y
x
O
2
注意:此题有两种情况.
小试牛刀
解:设一次函数的解析式为y=kx+b(k≠0)
∵一次函数y=kx+b的图象过点(0,2),
∴b=2
∵一次函数的图象与x轴的交点是(
,0),则
解得k=1或-1.
故此一次函数的解析式为y=x+2或y=-x+2.
典例精析
购买种子
数量/kg
0.5
1
1.5
2
2.5
3
3.5
4
…
付款金额/元
…
例2:“黄金1号”玉米种子的价格为5
元/kg,如果一次购买2
kg
以上的种子,超过2
kg
部分的种子的价格打8
折.
(1)填写下表:
2.5
5
7.5
10
12
14
16
18
典例精析
(2)写出购买量关于付款金额的函数解析式,并画出函数图象.
分析:从题目可知,种子的价格与
有关.
若购买种子量为x>2时,种子价格y为:
.
若购买种子量为0≤x≤2时,种子价格y为:
.
购买种子量
y=5x
y=4(x-2)+10=4x+2
典例精析
解:设购买量为x千克,付款金额为y元.
当x>2时,y=4(x-2)+10=4x+2.
当0≤x≤2时,y=5x;
(2)写出购买量关于付款金额的函数解析式,并画出函数图象.
叫做分段函数.注意:1.它是一个函数;2.要写明自变量取值范围.
y
=
5x(0≤x≤2)
4x+2(x>2)
{
y=5x(0≤x≤2)
y=4x+2(x>2)
y
x
O
1
2
10
3
14
典例精析
思考2:你能由上面的函数解析式或函数图象解决以下问题吗?
(1)一次购买1.5
kg
种子,需付款多少元?
(2)30元最多能购买多少种子?
解:(1)当0≤x≤2时,y=5x;
∴一次购买1.5
kg
种子,需付款5
×1.5=7.5元
(2)
∵
2
×5=10
<
30;
∴30元购买的种子超过2
kg
当x>2时,y=4x+2.
∴
4x+2=30,x=7
∴
30元最多能购买7
kg种子
小试牛刀
1、为节约用水,某市制定以下用水收费标准,每户每月用水不超过8立方米,每立方米收取1元外加0.3元的污水处理费;超过时,超过部分每立方米收取1.5元外加1.2元污水处理费,现设一户每月用水x立方米,应缴水费y元.
(1)求出y关于x的函数解析式;
解:y关于x的函数解析式为:
(1+0.3)x
=1.3x,
(0≤x≤8)
(1.5+1.2)(x-8)+1.3×8=2.7x-11.2.
(x>8)
y=
小试牛刀
(2)当x=10时,y=2.7×10-11.2=15.8.
(3)∵1.3×8=10.4<26.6,∴该用户用水量超过8立方米.
∴2.7x-11.2=26.6,解得x=14.
答:应缴水费为15.8元.
答:该户这月用水量为14立方米.
(2)该市一户某月若用水x=10立方米时,求应缴水费;
(3)该市一户某月缴水费26.6元,求该户这月用水量.
综合演练
1、正比例函数y=k1x与一次函数y=k2x+b的图象如图所示,它们的交点A的坐标为(3,4),并且OB=5.
(1)你能求出这两个函数的解析式吗?
(2)△AOB的面积是多少呢?
知识点拨:由OB=5可知点B的坐标为(0,-5).y=k1x的图象过点A(3,4),y=k2x+b的图象过点A(3,4),B(0,-5),代入解方程(组)即可.
综合演练
解:(1)
OB=5可知点B的坐标为(0,-5).
∵
y=k2x+b的图象过点A(3,4)、点B
(0,-5).
∴将点A(3,4)、点B
(0,-5)分别代入解析式中得:
解得:
∴y=3x-5
∵
y=k1x的图象过点A(3,4).
∴将点A(3,4)代入解析式中得3k1=4;解得:k1=
∴y=
x
3k2+b=4
b=-5
{
k2=3
b=-5
{
综合演练
(2)∵点A(3,4)
∴点A到y轴的距离为3
∴
△AOB的面积=
×3
×OB=
综合演练
2、已知一次函数y=kx+b(k≠0)的自变量的取值范围是-
3≤x≤
6,相应函数值的范围是-
5≤y≤
-
2
,求这个函数的解析式.
知识点拨:(1)当-
3≤x≤
6时,-
5≤y≤
-
2,实质是给出了两组自变量及对应的函数值;
(2)由于不知道函数的增减性,此题需分两种情况讨论.
综合演练
当k
>
0时,一次函数y=kx+b经过(-3,-2)、(6,-5)
将点(-3,-2)、(6,-5)分别代入解析式中得:
解得:
∴y=
x-3
-3k+b=-5
6k+b=-2
{
k=
b=-4
{
由题意可知:
当k<0时,一次函数y=kx+b经过(-3,-5)、(6,-2)
将点(-3,-5)、(6,-2)分别代入解析式中得:
解得:
∴y=
x-4
-3k+b=-2
6k+b=-5
{
k=
b=-3
{
综合演练
3、某医药研究所开发了一种新药,在实际验药时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(毫克)随时间x(时)的变化情况如图所示,当成年人按规定剂量服药后.
(1)服药后______时,血液中含药量最高,
达到每毫升_______毫克,接着逐步衰弱.
(2)服药6时,血液中含药量为每毫升____毫克.
x/时
y/毫克
8
4
2
6
O
2
8
4
综合演练
(3)当x≤2时y与x之间的函数解析式是___________.
(4)当x≥2时y与x之间的函数解析式是___________.
(5)如果每毫升血液中含药量4毫克或4毫克以上时,治疗疾病最有效,那么这个有效时间是______时.
y=4x
y=-x+8
4
x/时
y/毫克
8
4
2
6
O
课堂小结
本节课你有哪些收获?
1、什么是待定系数法?
2、如何利用待定系数法求函数的解析式?
课后作业
教材99页习题19.2第6、7、11题.
https://www.21cnjy.com/help/help_extract.php
