2020-2021学年度 人教版七年级数学下册 第五章 5.3.1.2 平行线的性质与判定的综合运用 同步练习(word版含答案)
文档属性
| 名称 | 2020-2021学年度 人教版七年级数学下册 第五章 5.3.1.2 平行线的性质与判定的综合运用 同步练习(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 163.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-18 18:49:49 | ||
图片预览

文档简介
第五章 相交线与平行线 5.3.1.2 平行线的性质与判定的综合运用
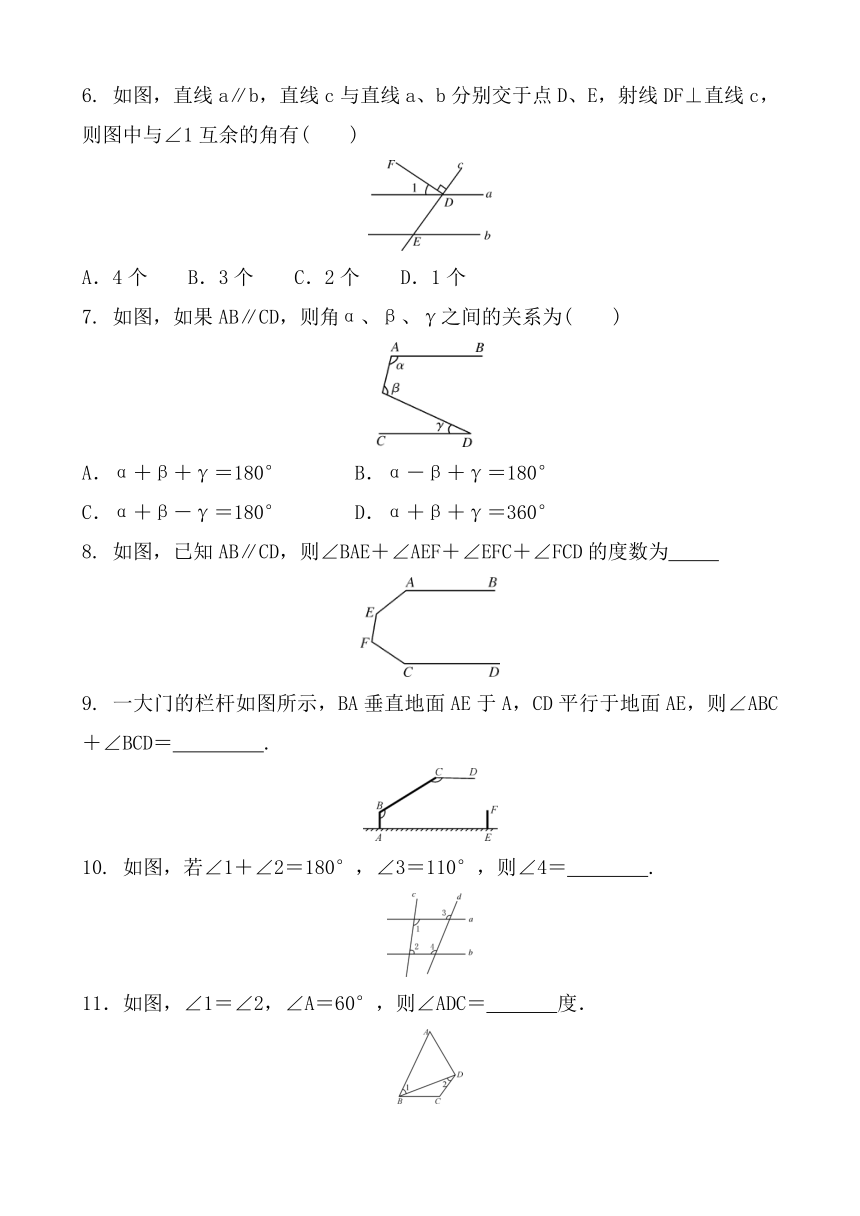
1.如图,直线a、b被直线c、d所截,若∠1=80°,∠2=100°,∠3=85°,则∠4的度数为( )
A.80° B.85° C.95° D.100°
2.如图,a、b、c为三条直线,且a⊥c,b⊥c,若∠1=70°,则∠2的度数为( )
A.70° B.90° C.110° D.80°
3.如图,已知两直线l1与l2被第三条直线l3所截,下列等式一定成立的是( )
A.∠1=∠2 B.∠2=∠3 C.∠2+∠4=180° D.∠1+∠4=180°
4. 如图,由A到B的方向是( )
A.南偏东30° B.南偏东60° C.北偏西30° D.北偏西60°
5. 如图,OC是∠AOB的平分线,l∥OB,若∠1=52°,则∠2的度数为( )
A.52° B.54° C.64° D.69°
6. 如图,直线a∥b,直线c与直线a、b分别交于点D、E,射线DF⊥直线c,则图中与∠1互余的角有( )
A.4个 B.3个 C.2个 D.1个
7. 如图,如果AB∥CD,则角α、β、γ之间的关系为( )
A.α+β+γ=180° B.α-β+γ=180°
C.α+β-γ=180° D.α+β+γ=360°
8. 如图,已知AB∥CD,则∠BAE+∠AEF+∠EFC+∠FCD的度数为
9. 一大门的栏杆如图所示,BA垂直地面AE于A,CD平行于地面AE,则∠ABC+∠BCD= .
10. 如图,若∠1+∠2=180°,∠3=110°,则∠4= .
11.如图,∠1=∠2,∠A=60°,则∠ADC= 度.
12. 如图,直线l1∥l2,∠α=∠β,∠1=40°,求∠2的度数.
13. 如图,已知四条直线a、b、c、d,∠1=79°,∠2=79°,∠3=101°.指出图中有哪些直线平行?说明理由,并求出α的度数.
14. 如图,已知∠1+∠2=180°,∠A=∠C.试判断AE与CF的位置关系,并说明理由.
15. 如图,放置在水平操场上的篮球架的横梁EF始终平行于AB, EF与上拉杆CF形成的∠F=150°,主柱AD垂直于地面.这一篮球架可以通过调整CF和后拉杆 BC 的位置来调整篮筐的高度.当∠CDB=35°时,且点H、D、B在同一直线上,求∠H 的度数.
16. 如图,已知∠1+∠2=180°,∠B=∠3,试判断∠AED与∠C的大小关系,并说明理由.
17. 已知AB∥CD,∠EAF=∠EAB,∠ECF=∠ECD.求证:∠AFC=∠AEC.
答案:
1---7 BADBC AC
8. 540°
9. 270°
10. 110°
11. 120
12. 解: 如图,延长AE交直线l2于点B,
∵l1∥l2,∴∠3=∠1=40°.∵∠α=∠β,∴AB∥CD,∴∠2+∠3=180°,
∴∠2=180°-∠3=180°-40°=140°.
13. 解:a∥b,c∥d,∵∠2=∠1=79°,∴a∥b,又∠4=∠3=101°,
∴∠2+∠4=180°,∴c∥d,∴∠α=∠1=79°.
14. 解:AE∥CF.理由:∵∠2=∠3,∠1+∠2=180°,∴∠1+∠3=180°,∴AB∥CD,∴∠EDC=∠A,∵∠A=∠C,∴∠C=∠EDC,∴AE∥FC.
15. 解:过点D作DI∥EF.因为∠F=150°,所以∠FDI=30°.所以∠ADB=180°-90°-30°-35°=25°.所以∠IDB=90°+25°=115°.因为GH∥AB,∴∠H=∠IDB=115°.
16. 解:∠AED=∠C,理由:∵∠1+∠2=180°,∠ADF+∠2=180°,
∴∠ADF=∠1,∴AB∥EF,∴∠ADE=∠3,又∠B=∠3,∴∠ADE=∠B,∴DE∥BC,∴∠AED=∠C.
17. 证明:分别过点E、F作ME∥AB,NF∥AB,∵∠EAF=∠EAB,∠ECF=∠ECD,设∠EAF=x,∠ECF=y,则∠EAB=4x,∠ECD=4y,故∠BAF=3x,∠DCF=3y,∵AB∥CD,ME∥AB,NF∥AB,∴AB∥ME∥NF∥CD,∴∠BAF=∠AFN=3x,∠BAE=∠AEM=4x,∠MEC=∠ECD=4y,∠NFC=∠FCD=3y,∴∠AEC=∠AEM+∠MEC=4(x+y),∠AFC=∠AFN+∠NFC=3(x+y),∴∠AFC=∠AEC.
1.如图,直线a、b被直线c、d所截,若∠1=80°,∠2=100°,∠3=85°,则∠4的度数为( )
A.80° B.85° C.95° D.100°
2.如图,a、b、c为三条直线,且a⊥c,b⊥c,若∠1=70°,则∠2的度数为( )
A.70° B.90° C.110° D.80°
3.如图,已知两直线l1与l2被第三条直线l3所截,下列等式一定成立的是( )
A.∠1=∠2 B.∠2=∠3 C.∠2+∠4=180° D.∠1+∠4=180°
4. 如图,由A到B的方向是( )
A.南偏东30° B.南偏东60° C.北偏西30° D.北偏西60°
5. 如图,OC是∠AOB的平分线,l∥OB,若∠1=52°,则∠2的度数为( )
A.52° B.54° C.64° D.69°
6. 如图,直线a∥b,直线c与直线a、b分别交于点D、E,射线DF⊥直线c,则图中与∠1互余的角有( )
A.4个 B.3个 C.2个 D.1个
7. 如图,如果AB∥CD,则角α、β、γ之间的关系为( )
A.α+β+γ=180° B.α-β+γ=180°
C.α+β-γ=180° D.α+β+γ=360°
8. 如图,已知AB∥CD,则∠BAE+∠AEF+∠EFC+∠FCD的度数为
9. 一大门的栏杆如图所示,BA垂直地面AE于A,CD平行于地面AE,则∠ABC+∠BCD= .
10. 如图,若∠1+∠2=180°,∠3=110°,则∠4= .
11.如图,∠1=∠2,∠A=60°,则∠ADC= 度.
12. 如图,直线l1∥l2,∠α=∠β,∠1=40°,求∠2的度数.
13. 如图,已知四条直线a、b、c、d,∠1=79°,∠2=79°,∠3=101°.指出图中有哪些直线平行?说明理由,并求出α的度数.
14. 如图,已知∠1+∠2=180°,∠A=∠C.试判断AE与CF的位置关系,并说明理由.
15. 如图,放置在水平操场上的篮球架的横梁EF始终平行于AB, EF与上拉杆CF形成的∠F=150°,主柱AD垂直于地面.这一篮球架可以通过调整CF和后拉杆 BC 的位置来调整篮筐的高度.当∠CDB=35°时,且点H、D、B在同一直线上,求∠H 的度数.
16. 如图,已知∠1+∠2=180°,∠B=∠3,试判断∠AED与∠C的大小关系,并说明理由.
17. 已知AB∥CD,∠EAF=∠EAB,∠ECF=∠ECD.求证:∠AFC=∠AEC.
答案:
1---7 BADBC AC
8. 540°
9. 270°
10. 110°
11. 120
12. 解: 如图,延长AE交直线l2于点B,
∵l1∥l2,∴∠3=∠1=40°.∵∠α=∠β,∴AB∥CD,∴∠2+∠3=180°,
∴∠2=180°-∠3=180°-40°=140°.
13. 解:a∥b,c∥d,∵∠2=∠1=79°,∴a∥b,又∠4=∠3=101°,
∴∠2+∠4=180°,∴c∥d,∴∠α=∠1=79°.
14. 解:AE∥CF.理由:∵∠2=∠3,∠1+∠2=180°,∴∠1+∠3=180°,∴AB∥CD,∴∠EDC=∠A,∵∠A=∠C,∴∠C=∠EDC,∴AE∥FC.
15. 解:过点D作DI∥EF.因为∠F=150°,所以∠FDI=30°.所以∠ADB=180°-90°-30°-35°=25°.所以∠IDB=90°+25°=115°.因为GH∥AB,∴∠H=∠IDB=115°.
16. 解:∠AED=∠C,理由:∵∠1+∠2=180°,∠ADF+∠2=180°,
∴∠ADF=∠1,∴AB∥EF,∴∠ADE=∠3,又∠B=∠3,∴∠ADE=∠B,∴DE∥BC,∴∠AED=∠C.
17. 证明:分别过点E、F作ME∥AB,NF∥AB,∵∠EAF=∠EAB,∠ECF=∠ECD,设∠EAF=x,∠ECF=y,则∠EAB=4x,∠ECD=4y,故∠BAF=3x,∠DCF=3y,∵AB∥CD,ME∥AB,NF∥AB,∴AB∥ME∥NF∥CD,∴∠BAF=∠AFN=3x,∠BAE=∠AEM=4x,∠MEC=∠ECD=4y,∠NFC=∠FCD=3y,∴∠AEC=∠AEM+∠MEC=4(x+y),∠AFC=∠AFN+∠NFC=3(x+y),∴∠AFC=∠AEC.
