2020——2021学年北师大版八年级下册数学 1.3线段的垂直平分线 同步测试(Word版 含解析)
文档属性
| 名称 | 2020——2021学年北师大版八年级下册数学 1.3线段的垂直平分线 同步测试(Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 125.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-19 00:00:00 | ||
图片预览


文档简介
1.3线段的垂直平分线 同步测试
一.选择题
1.如图,在△ABC中,∠A=87°,∠ABC的平分线BD交AC于点D,E是BC中点,且DE⊥BC,那么∠C的度数为( )
A.16° B.28° C.31° D.62°
2.如图,DE是△ABC中AC边的垂直平分线,若BC=4cm,AB=5cm,则△EBC的周长为( )
A.8cm B.9cm C.10cm D.11cm
3.如图是“一带一路”示意图,若记北京为A地,莫斯科为B地,雅典为C地,分别连接AB、AC、BC,形成了一个三角形.若想建立一个货物中转仓,使其到A、B、C三地的距离相等,则中转仓的位置应选在( )
A.三边垂直平分线的交点 B.三边中线的交点
C.三条角平分线的交点 D.三边上高的交点
4.如图,在△ABC中,AD⊥BC,垂足为D,EF垂直平分AC,交AC于点F,交BC于点E,BD=DE,若△ABC的周长为26cm,AF=5cm,则DC的长为( )
A.8cm B.7cm C.10cm D.9cm
5.如图,∠B=35°,CD为AB的垂直平分线,则∠ACE=( )
A.55° B.60° C.70° D.80°
6.如图,已知△ABC的三条内角平分线相交于点I,三边的垂直平分线相交于点O.若∠BOC=148°,则∠BIC=( )
A.120° B.125° C.127° D.132°
7.在△ABC中,边AB,BC的垂直平分线l1、l2相交于点P,若∠PAC=x°,则∠1的度数是( )°.
A.90﹣x B.x C.90﹣x D.60﹣x
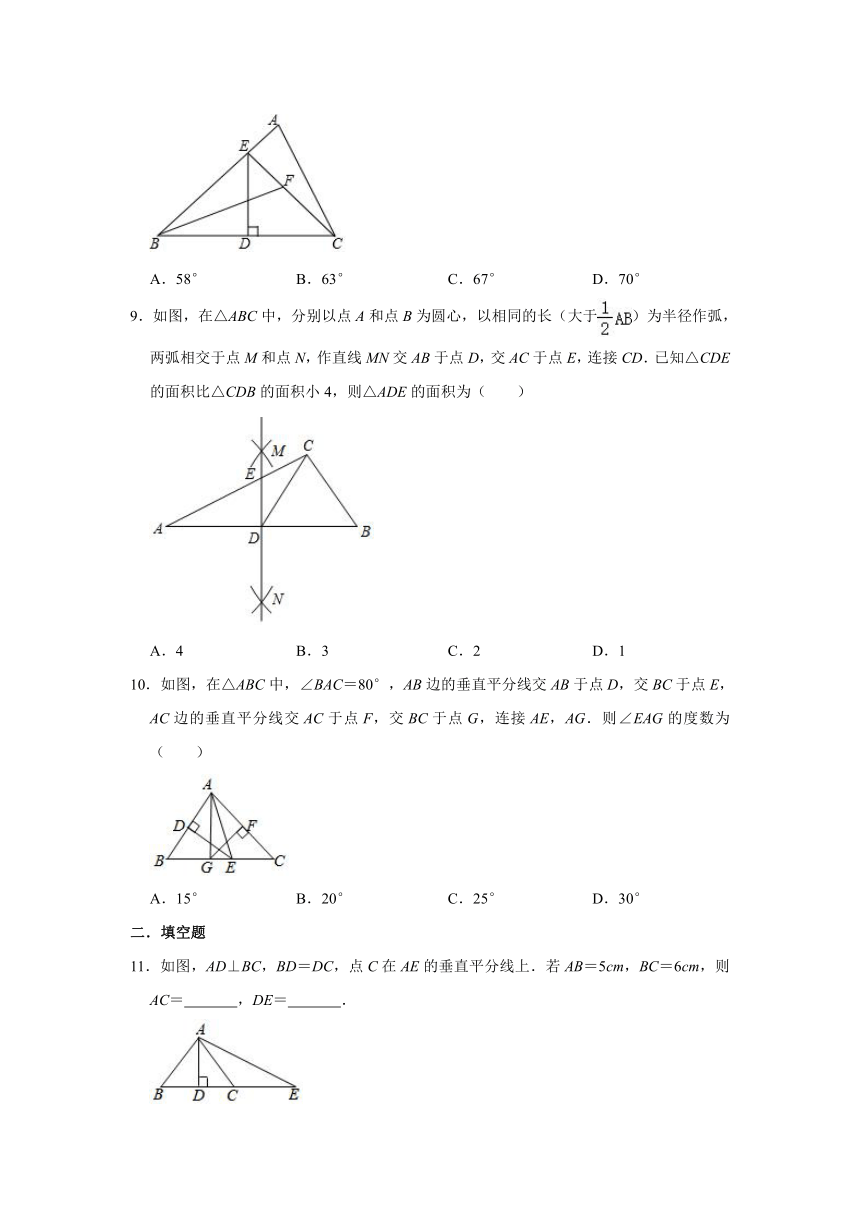
8.如图,在△ABC中,DE垂直平分BC,分别交BC、AB于D、E,连接CE,BF平分∠ABC,交CE于F,若BE=AC,∠ACE=12°,则∠EFB的度数为( )
A.58° B.63° C.67° D.70°
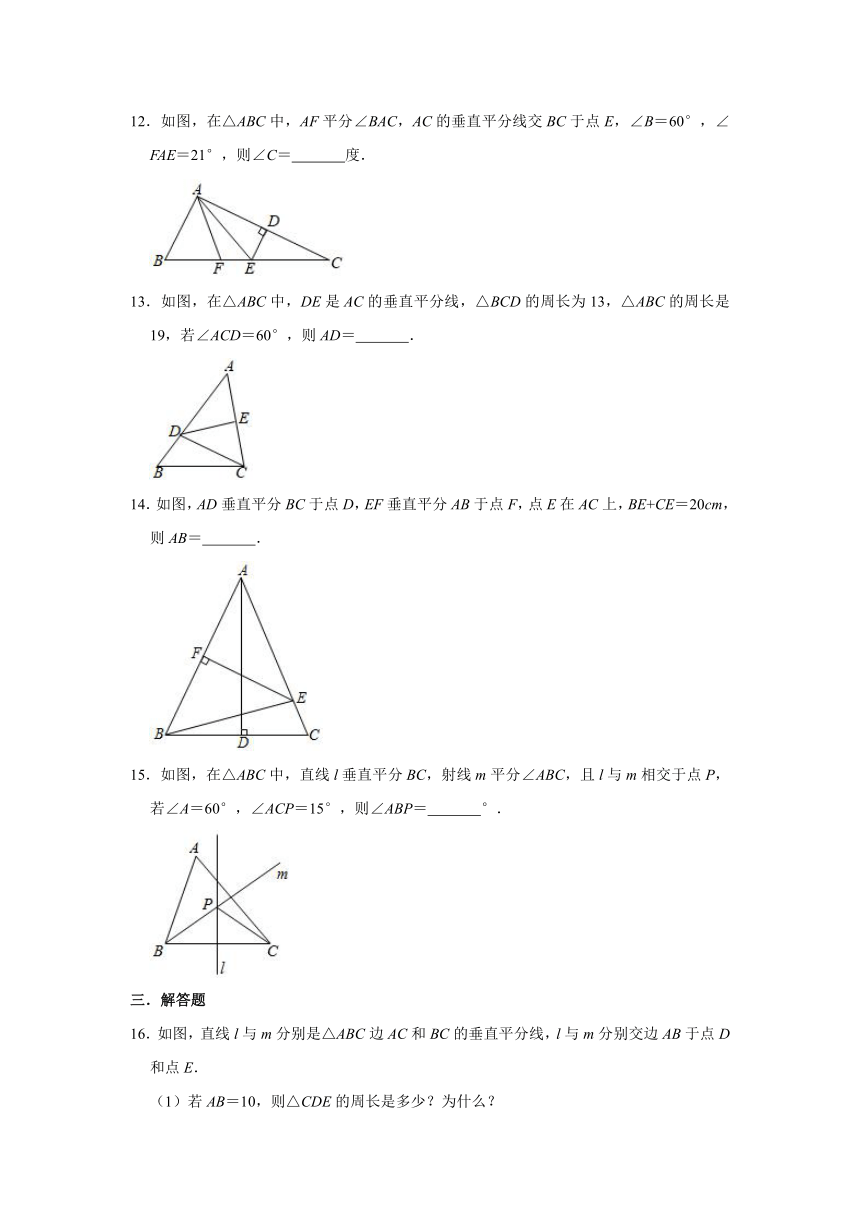
9.如图,在△ABC中,分别以点A和点B为圆心,以相同的长(大于)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交AC于点E,连接CD.已知△CDE的面积比△CDB的面积小4,则△ADE的面积为( )
A.4 B.3 C.2 D.1
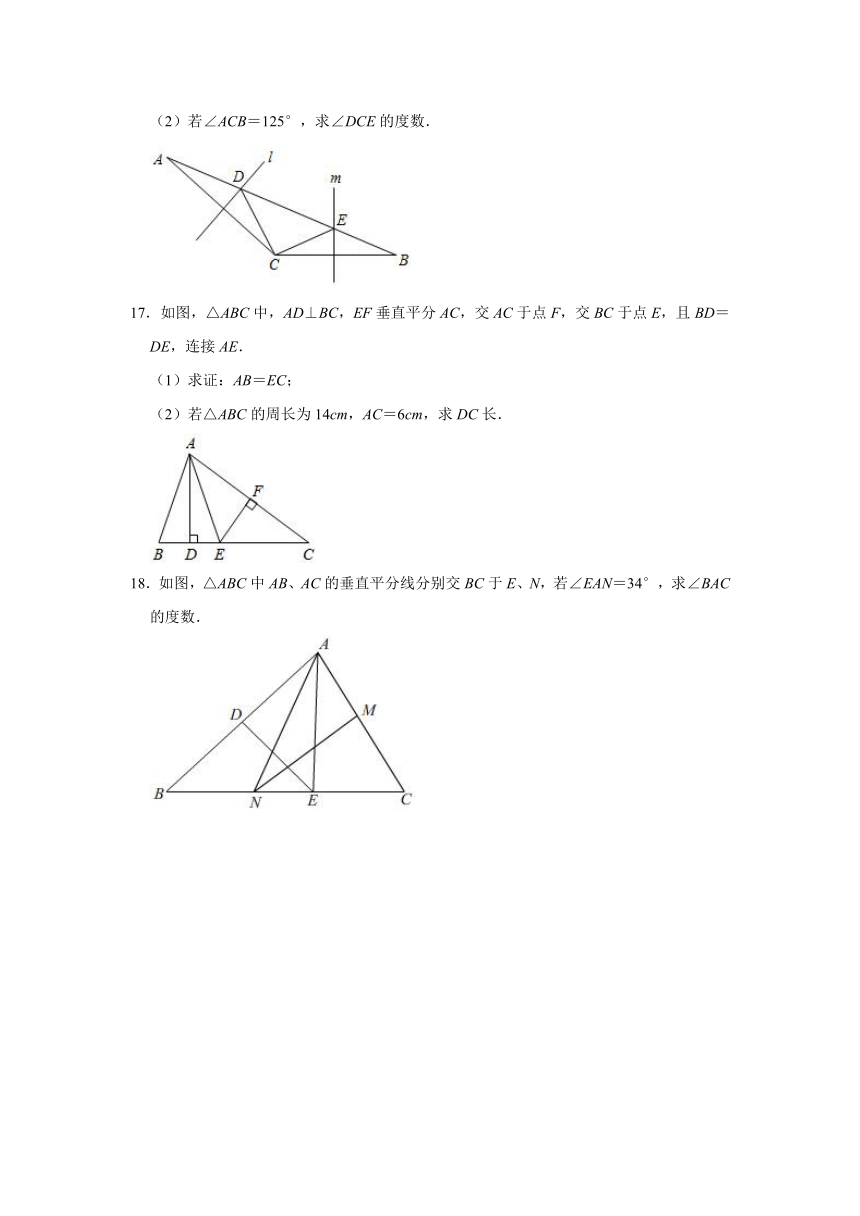
10.如图,在△ABC中,∠BAC=80°,AB边的垂直平分线交AB于点D,交BC于点E,AC边的垂直平分线交AC于点F,交BC于点G,连接AE,AG.则∠EAG的度数为( )
A.15° B.20° C.25° D.30°
二.填空题
11.如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上.若AB=5cm,BC=6cm,则AC= ,DE= .
12.如图,在△ABC中,AF平分∠BAC,AC的垂直平分线交BC于点E,∠B=60°,∠FAE=21°,则∠C= 度.
13.如图,在△ABC中,DE是AC的垂直平分线,△BCD的周长为13,△ABC的周长是19,若∠ACD=60°,则AD= .
14.如图,AD垂直平分BC于点D,EF垂直平分AB于点F,点E在AC上,BE+CE=20cm,则AB= .
15.如图,在△ABC中,直线l垂直平分BC,射线m平分∠ABC,且l与m相交于点P,若∠A=60°,∠ACP=15°,则∠ABP= °.
三.解答题
16.如图,直线l与m分别是△ABC边AC和BC的垂直平分线,l与m分别交边AB于点D和点E.
(1)若AB=10,则△CDE的周长是多少?为什么?
(2)若∠ACB=125°,求∠DCE的度数.
17.如图,△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE,连接AE.
(1)求证:AB=EC;
(2)若△ABC的周长为14cm,AC=6cm,求DC长.
18.如图,△ABC中AB、AC的垂直平分线分别交BC于E、N,若∠EAN=34°,求∠BAC的度数.
参考答案
一.选择题
1.解:∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵DE⊥BC,E是BC中点,
∴DB=DC,
∴∠DBC=∠C,
∴∠ABD=∠CBD=∠C,
∴∠ABD+∠CBD+∠C=180°﹣87°,
解得,∠C=31°,
故选:C.
2.解:∵DE是△ABC中AC边的垂直平分线,
∴AE=CE,
∴AE+BE=CE+BE=AB=5cm,
∴△EBC的周长=BC+BE+CE=5+4=9(cm).
故选:B.
3.解:∵中转仓到A、B、C三地的距离相等,
∴中转仓的位置应选在△ABC三边的垂直平分线的交点处,
故选:A.
4.解:∵AD⊥BC,BD=DE,EF垂直平分AC,
∴AB=AE=EC,
∵△ABC周长26cm,AF=5cm,
∴AC=10(cm),
∴AB+BC=16(cm),
∴AB+BE+EC=16(cm),
即2DE+2EC=16(cm),
∴DE+EC=8(cm),
∴DC=DE+EC=8(cm),
故选:A.
5.解:∵CD为AB的垂直平分线,
∴AC=BC,
∴∠B=∠A=35°
∴∠ACE=∠B+∠A=70°.
故选:C.
6.解:连接OA,
∵∠BOC=148°,
∴∠OBC+∠OCB=180°﹣∠BOC=32°,
∵O是三边的垂直平分线的交点,
∴OA=OB=OC,
∴∠OAB=∠OBA,∠OAC=∠OCA,
∴∠OBA+∠OCA=(180°﹣32°)÷2=74°,
∴∠ABC+∠ACB=74°+32°=106°,
∵△ABC的三条内角平分线相交于点I,
∴∠IBC=∠ABC,∠ICB=∠ACB,
∴∠BIC=180°﹣∠IBC﹣∠ICB=180°﹣(∠ABC+∠ACB)=127°,
故选:C.
7.解:连接PB、PC,
∵边AB,BC的垂直平分线l1、l2相交于点P,
∴PA=PB,PB=PC,
∴∠PBA=∠PAB,∠PBC=∠PCB,PA=PC,
∴∠PCA=∠PAC=x°,∠PAB+∠PCB=∠PBA+∠PBC=∠B,
∴2∠B+2x°=180°,
解得,∠B=90°﹣x°,
∴∠DPE=180°﹣∠B=90°+x°,
∴∠1=180°﹣∠DPE=90°﹣x°,
故选:A.
8.解:∵DE垂直平分BC,
∴EB=EC,
∴∠EBC=∠ECB,
∵EB=EC,BE=AC,
∴AC=EC,
∴∠AEC=∠EAC=×(180°﹣12°)=84°,
∴∠EBC=∠ECB=∠AEC=42°,
∵BF平分∠ABC,
∴∠EBF=∠CBF=21°,
∴∠EFB=∠AEC﹣∠EBF=63°,
故选:B.
9.解:由尺规作图可知,MN是线段AB的垂直平分线,
∴点D是AB的中点,
∴S△ADC=S△BDC,
∵S△BDC﹣S△CDE=4,
∴S△ADC﹣S△CDE=4,即△ADE的面积为4,
故选:A.
10.解:∵AB边的垂直平分线交AB于点D,AC边的垂直平分线交AC于点F,
∴AG=CG,AE=BE,
∴∠C=∠CAG,∠B=∠BAE,
∴∠BAE+∠CAG=∠B+∠C=180°﹣∠BAC=100°,
∴∠EAG=∠BAE+∠CAG﹣∠BAC=100°﹣80°=20°,
故选:B.
二.填空题
11.解:∵BC=6cm,
∴BD=DC=3(cm),
∵AD⊥BC,BD=DC,AB=5cm,
∴AC=AB=5(cm),
∵点C在AE的垂直平分线上,
∴EC=AC=5(cm),
∴DE=DC+EC=8(cm),
故答案为:5cm;8cm.
12.解:设∠C=x,
∵DE是线段AC的垂直平分线,
∴EA=EC,
∴∠EAC=∠C=x,
∴∠FAC=x+21°,
∵AF平分∠BAC,
∴∠BAF=∠FAC=x+21°,
∴x+x+21°+x+21°+60°=180°,
解得,x=26°,即∠C=x=26°,
故答案为:26.
13.解:∵DE是AC的垂直平分线,
∴DA=DC,
∵∠ACD=60°,
∴△ADC为等边三角形,
∴AD=AC,
∵△ABC的周长是19,
∴AB+BC+AC=19,
∵△BCD的周长为13,
∴BD+DC+BC=BD+DA+BC=AB+BC=13,
∴AC=19﹣13=6,
∴AD=AC=6,
故答案为:6.
14.解:∵EF垂直平分AB于点F,
∴AE=BE,
∵BE+CE=20cm,
∴AE+CE=20cm,
即AC=20cm,
∵AD垂直平分BC于点D,
∴AB=AC=20cm,
故答案为:20cm.
15.解:设∠ABP=x,
∵BP平分∠ABC,
∴∠CBP=∠ABP=x,
∵直线l垂直平分BC,
∴PB=PC,
∴∠PCB=∠CBP=x,
∴60°+15°+x+x+x=180°,
解得,x=35°,即∠ABP=35°,
故答案为:35.
三.解答题
16.解:(1)△CDE的周长为10.
∵直线l与m分别是△ABC边AC和BC的垂直平分线,
∴AD=CD,BE=CE,
∴△CDE的周长=CD+DE+CE=AD+DE+BE=AB=10;
(2)∵直线l与m分别是△ABC边AC和BC的垂直平分线,
∴AD=CD,BE=CE,
∴∠A=∠ACD,∠B=∠BCE,
又∵∠ACB=125°,
∴∠A+∠B=180°﹣125°=55°,
∴∠ACD+∠BCE=55°,
∴∠DCE=∠ACB﹣(∠ACD+∠BCE)=125°﹣55°=70°.
17.(1)证明:∵EF垂直平分AC,
∴AE=EC,
∵AD⊥BC,BD=DE,
∴AB=AE,
∴AB=EC;
(2)解:∵△ABC的周长为14cm,
∴AB+BC+AC=14(cm),
∵AC=6cm,
∴AB+BC=8(cm),
∵AB=EC,BD=DE,
∴DC=DE+EC=(AB+BC)=4(cm).
18.解:∵AB、AC的垂直平分线分别交BC于点E、N,
∴AE=BE,AN=CN,
∴∠BAE=∠B,∠CAN=∠C,
∵∠AEC=∠BAE+∠B=2∠BAE,∠ANB=∠CAN+∠C=2∠CAN,
∵∠EAN=34°,
∴∠AEN+∠ANE=180°﹣∠EAN=146°,
∵∠AEN=180°﹣2∠BAE,∠ANE=180°﹣2∠CAN,
∴180°﹣2∠BAE+180°﹣2∠CAN=146°,
∴∠B+∠C=107°,
∴∠BAC=180°﹣107°=73°.
一.选择题
1.如图,在△ABC中,∠A=87°,∠ABC的平分线BD交AC于点D,E是BC中点,且DE⊥BC,那么∠C的度数为( )
A.16° B.28° C.31° D.62°
2.如图,DE是△ABC中AC边的垂直平分线,若BC=4cm,AB=5cm,则△EBC的周长为( )
A.8cm B.9cm C.10cm D.11cm
3.如图是“一带一路”示意图,若记北京为A地,莫斯科为B地,雅典为C地,分别连接AB、AC、BC,形成了一个三角形.若想建立一个货物中转仓,使其到A、B、C三地的距离相等,则中转仓的位置应选在( )
A.三边垂直平分线的交点 B.三边中线的交点
C.三条角平分线的交点 D.三边上高的交点
4.如图,在△ABC中,AD⊥BC,垂足为D,EF垂直平分AC,交AC于点F,交BC于点E,BD=DE,若△ABC的周长为26cm,AF=5cm,则DC的长为( )
A.8cm B.7cm C.10cm D.9cm
5.如图,∠B=35°,CD为AB的垂直平分线,则∠ACE=( )
A.55° B.60° C.70° D.80°
6.如图,已知△ABC的三条内角平分线相交于点I,三边的垂直平分线相交于点O.若∠BOC=148°,则∠BIC=( )
A.120° B.125° C.127° D.132°
7.在△ABC中,边AB,BC的垂直平分线l1、l2相交于点P,若∠PAC=x°,则∠1的度数是( )°.
A.90﹣x B.x C.90﹣x D.60﹣x
8.如图,在△ABC中,DE垂直平分BC,分别交BC、AB于D、E,连接CE,BF平分∠ABC,交CE于F,若BE=AC,∠ACE=12°,则∠EFB的度数为( )
A.58° B.63° C.67° D.70°
9.如图,在△ABC中,分别以点A和点B为圆心,以相同的长(大于)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交AC于点E,连接CD.已知△CDE的面积比△CDB的面积小4,则△ADE的面积为( )
A.4 B.3 C.2 D.1
10.如图,在△ABC中,∠BAC=80°,AB边的垂直平分线交AB于点D,交BC于点E,AC边的垂直平分线交AC于点F,交BC于点G,连接AE,AG.则∠EAG的度数为( )
A.15° B.20° C.25° D.30°
二.填空题
11.如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上.若AB=5cm,BC=6cm,则AC= ,DE= .
12.如图,在△ABC中,AF平分∠BAC,AC的垂直平分线交BC于点E,∠B=60°,∠FAE=21°,则∠C= 度.
13.如图,在△ABC中,DE是AC的垂直平分线,△BCD的周长为13,△ABC的周长是19,若∠ACD=60°,则AD= .
14.如图,AD垂直平分BC于点D,EF垂直平分AB于点F,点E在AC上,BE+CE=20cm,则AB= .
15.如图,在△ABC中,直线l垂直平分BC,射线m平分∠ABC,且l与m相交于点P,若∠A=60°,∠ACP=15°,则∠ABP= °.
三.解答题
16.如图,直线l与m分别是△ABC边AC和BC的垂直平分线,l与m分别交边AB于点D和点E.
(1)若AB=10,则△CDE的周长是多少?为什么?
(2)若∠ACB=125°,求∠DCE的度数.
17.如图,△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE,连接AE.
(1)求证:AB=EC;
(2)若△ABC的周长为14cm,AC=6cm,求DC长.
18.如图,△ABC中AB、AC的垂直平分线分别交BC于E、N,若∠EAN=34°,求∠BAC的度数.
参考答案
一.选择题
1.解:∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵DE⊥BC,E是BC中点,
∴DB=DC,
∴∠DBC=∠C,
∴∠ABD=∠CBD=∠C,
∴∠ABD+∠CBD+∠C=180°﹣87°,
解得,∠C=31°,
故选:C.
2.解:∵DE是△ABC中AC边的垂直平分线,
∴AE=CE,
∴AE+BE=CE+BE=AB=5cm,
∴△EBC的周长=BC+BE+CE=5+4=9(cm).
故选:B.
3.解:∵中转仓到A、B、C三地的距离相等,
∴中转仓的位置应选在△ABC三边的垂直平分线的交点处,
故选:A.
4.解:∵AD⊥BC,BD=DE,EF垂直平分AC,
∴AB=AE=EC,
∵△ABC周长26cm,AF=5cm,
∴AC=10(cm),
∴AB+BC=16(cm),
∴AB+BE+EC=16(cm),
即2DE+2EC=16(cm),
∴DE+EC=8(cm),
∴DC=DE+EC=8(cm),
故选:A.
5.解:∵CD为AB的垂直平分线,
∴AC=BC,
∴∠B=∠A=35°
∴∠ACE=∠B+∠A=70°.
故选:C.
6.解:连接OA,
∵∠BOC=148°,
∴∠OBC+∠OCB=180°﹣∠BOC=32°,
∵O是三边的垂直平分线的交点,
∴OA=OB=OC,
∴∠OAB=∠OBA,∠OAC=∠OCA,
∴∠OBA+∠OCA=(180°﹣32°)÷2=74°,
∴∠ABC+∠ACB=74°+32°=106°,
∵△ABC的三条内角平分线相交于点I,
∴∠IBC=∠ABC,∠ICB=∠ACB,
∴∠BIC=180°﹣∠IBC﹣∠ICB=180°﹣(∠ABC+∠ACB)=127°,
故选:C.
7.解:连接PB、PC,
∵边AB,BC的垂直平分线l1、l2相交于点P,
∴PA=PB,PB=PC,
∴∠PBA=∠PAB,∠PBC=∠PCB,PA=PC,
∴∠PCA=∠PAC=x°,∠PAB+∠PCB=∠PBA+∠PBC=∠B,
∴2∠B+2x°=180°,
解得,∠B=90°﹣x°,
∴∠DPE=180°﹣∠B=90°+x°,
∴∠1=180°﹣∠DPE=90°﹣x°,
故选:A.
8.解:∵DE垂直平分BC,
∴EB=EC,
∴∠EBC=∠ECB,
∵EB=EC,BE=AC,
∴AC=EC,
∴∠AEC=∠EAC=×(180°﹣12°)=84°,
∴∠EBC=∠ECB=∠AEC=42°,
∵BF平分∠ABC,
∴∠EBF=∠CBF=21°,
∴∠EFB=∠AEC﹣∠EBF=63°,
故选:B.
9.解:由尺规作图可知,MN是线段AB的垂直平分线,
∴点D是AB的中点,
∴S△ADC=S△BDC,
∵S△BDC﹣S△CDE=4,
∴S△ADC﹣S△CDE=4,即△ADE的面积为4,
故选:A.
10.解:∵AB边的垂直平分线交AB于点D,AC边的垂直平分线交AC于点F,
∴AG=CG,AE=BE,
∴∠C=∠CAG,∠B=∠BAE,
∴∠BAE+∠CAG=∠B+∠C=180°﹣∠BAC=100°,
∴∠EAG=∠BAE+∠CAG﹣∠BAC=100°﹣80°=20°,
故选:B.
二.填空题
11.解:∵BC=6cm,
∴BD=DC=3(cm),
∵AD⊥BC,BD=DC,AB=5cm,
∴AC=AB=5(cm),
∵点C在AE的垂直平分线上,
∴EC=AC=5(cm),
∴DE=DC+EC=8(cm),
故答案为:5cm;8cm.
12.解:设∠C=x,
∵DE是线段AC的垂直平分线,
∴EA=EC,
∴∠EAC=∠C=x,
∴∠FAC=x+21°,
∵AF平分∠BAC,
∴∠BAF=∠FAC=x+21°,
∴x+x+21°+x+21°+60°=180°,
解得,x=26°,即∠C=x=26°,
故答案为:26.
13.解:∵DE是AC的垂直平分线,
∴DA=DC,
∵∠ACD=60°,
∴△ADC为等边三角形,
∴AD=AC,
∵△ABC的周长是19,
∴AB+BC+AC=19,
∵△BCD的周长为13,
∴BD+DC+BC=BD+DA+BC=AB+BC=13,
∴AC=19﹣13=6,
∴AD=AC=6,
故答案为:6.
14.解:∵EF垂直平分AB于点F,
∴AE=BE,
∵BE+CE=20cm,
∴AE+CE=20cm,
即AC=20cm,
∵AD垂直平分BC于点D,
∴AB=AC=20cm,
故答案为:20cm.
15.解:设∠ABP=x,
∵BP平分∠ABC,
∴∠CBP=∠ABP=x,
∵直线l垂直平分BC,
∴PB=PC,
∴∠PCB=∠CBP=x,
∴60°+15°+x+x+x=180°,
解得,x=35°,即∠ABP=35°,
故答案为:35.
三.解答题
16.解:(1)△CDE的周长为10.
∵直线l与m分别是△ABC边AC和BC的垂直平分线,
∴AD=CD,BE=CE,
∴△CDE的周长=CD+DE+CE=AD+DE+BE=AB=10;
(2)∵直线l与m分别是△ABC边AC和BC的垂直平分线,
∴AD=CD,BE=CE,
∴∠A=∠ACD,∠B=∠BCE,
又∵∠ACB=125°,
∴∠A+∠B=180°﹣125°=55°,
∴∠ACD+∠BCE=55°,
∴∠DCE=∠ACB﹣(∠ACD+∠BCE)=125°﹣55°=70°.
17.(1)证明:∵EF垂直平分AC,
∴AE=EC,
∵AD⊥BC,BD=DE,
∴AB=AE,
∴AB=EC;
(2)解:∵△ABC的周长为14cm,
∴AB+BC+AC=14(cm),
∵AC=6cm,
∴AB+BC=8(cm),
∵AB=EC,BD=DE,
∴DC=DE+EC=(AB+BC)=4(cm).
18.解:∵AB、AC的垂直平分线分别交BC于点E、N,
∴AE=BE,AN=CN,
∴∠BAE=∠B,∠CAN=∠C,
∵∠AEC=∠BAE+∠B=2∠BAE,∠ANB=∠CAN+∠C=2∠CAN,
∵∠EAN=34°,
∴∠AEN+∠ANE=180°﹣∠EAN=146°,
∵∠AEN=180°﹣2∠BAE,∠ANE=180°﹣2∠CAN,
∴180°﹣2∠BAE+180°﹣2∠CAN=146°,
∴∠B+∠C=107°,
∴∠BAC=180°﹣107°=73°.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
