2020-2021学年九年级数学北师大版下册第三章《圆》单元测试卷(word含答案)
文档属性
| 名称 | 2020-2021学年九年级数学北师大版下册第三章《圆》单元测试卷(word含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 170.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-18 00:00:00 | ||
图片预览

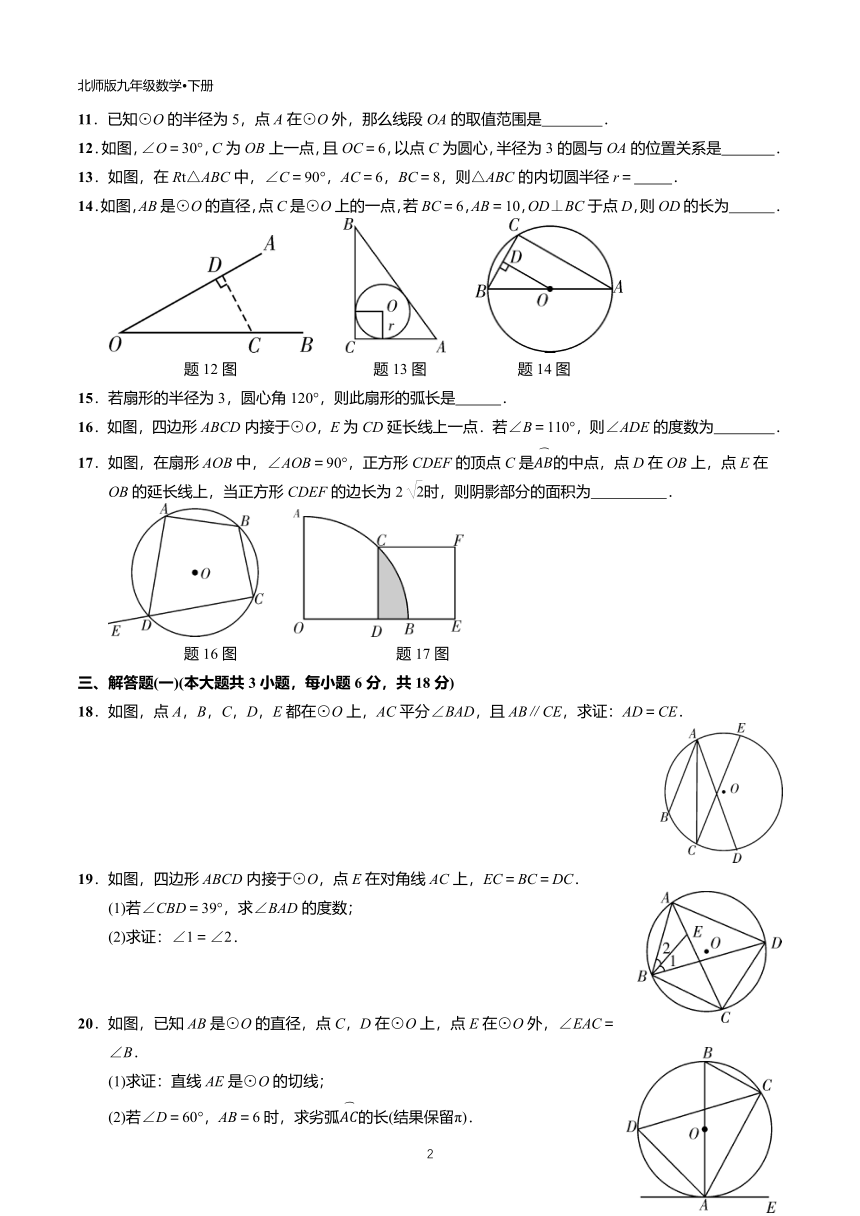
文档简介
北师版九年级数学?下册
第三章《圆》单元测试卷
(时间90分钟,满分120分)
班级________
姓名________
学号________
成绩________
一、选择题(本大题10小题,每小题3分,共30分)
1.在△ABC中,∠C=90°,AB=5,BC=4,以A为圆心,以3为半径作图,则点C与⊙A的位置关系为(
)
A.点C在⊙A内
B.点C在⊙A上
C.点C在⊙A外
D.点C在⊙A上或点C在⊙A外
2.下列语句中,正确的有(
)
①相等的圆心角所对的弧相等;②平分弦的直径垂直于弦;③长度相等的两条弧是等弧;④圆是轴对称图形,任何一条直径都是对称轴.
A.0个
B.1个
C.2个
D.3个
3.如图,点A,B,C都在⊙O上,若∠C=35°,则∠AOB的度数为(
)
A.35°
B.55°
C.145°
D.70°
4.如图,在⊙O中,弦AB的长为16cm,圆心O到AB的距离为6
m,则⊙O的半径是(
)
A.6cm
B.10cm
C.8cm
D.20cm
5.如图,⊙O是△ABC的外接圆,弦AC的长为3,sin
B=,则⊙O的半径为(
)
A.4
B.3
C.2
D.
6.如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于D,且CO=CD,则∠PCA=(
)
A.30°
B.45°
C.60°
D.67.5°
题3图
题4图
题5图
题6图
7.扇形的弧长为20πcm,面积为240πcm2,那么扇形的半径是(
)
A.6cm
B.12cm
C.24cm
D.28cm
8.一个圆锥的底面半径是6cm,其侧面展开图为半圆,则圆锥的母线长为(
)
A.9cm
B.12cm
C.15cm
D.18cm
9.⊙O的半径是13,弦AB∥CD,AB=24,CD=10,则AB与CD的距离是(
)
A.7
B.17
C.7或17
D.34
10.如图,在Rt△ABC中,∠A=30°,BC=2,以直角边AC为直径作⊙O交AB于点D,则图中阴影部分的面积是(
)
A.-π
B.-π
C.-
D.-
二、填空题(本大题共7小题,每小题4分,共28分)
11.已知⊙O的半径为5,点A在⊙O外,那么线段OA的取值范围是
.
12.如图,∠O=30°,C为OB上一点,且OC=6,以点C为圆心,半径为3的圆与OA的位置关系是
.
13.如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,则△ABC的内切圆半径r=
.
14.如图,AB是⊙O的直径,点C是⊙O上的一点,若BC=6,AB=10,OD⊥BC于点D,则OD的长为
.
题12图
题13图
题14图
15.若扇形的半径为3,圆心角120°,则此扇形的弧长是
.
16.如图,四边形ABCD内接于⊙O,E为CD延长线上一点.若∠B=110°,则∠ADE的度数为
.
17.如图,在扇形AOB中,∠AOB=90°,正方形CDEF的顶点C是的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2时,则阴影部分的面积为
.
题16图
题17图
三、解答题(一)(本大题共3小题,每小题6分,共18分)
18.如图,点A,B,C,D,E都在⊙O上,AC平分∠BAD,且AB∥CE,求证:AD=CE.
19.如图,四边形ABCD内接于⊙O,点E在对角线AC上,EC=BC=DC.
(1)若∠CBD=39°,求∠BAD的度数;
(2)求证:∠1=∠2.
20.如图,已知AB是⊙O的直径,点C,D在⊙O上,点E在⊙O外,∠EAC=∠B.
(1)求证:直线AE是⊙O的切线;
(2)若∠D=60°,AB=6时,求劣弧的长(结果保留π).
四、解答题(二)(本大题共3小题,每小题8分,共24分)
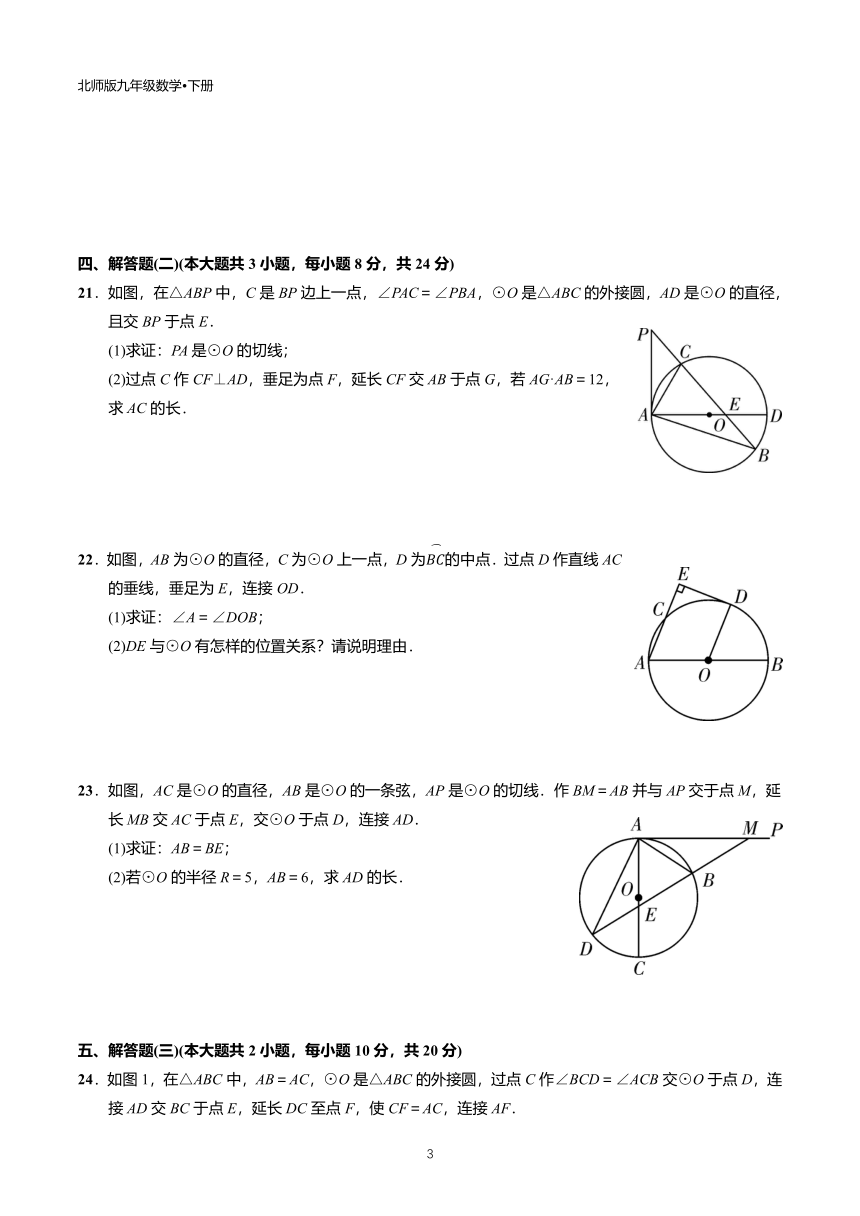
21.如图,在△ABP中,C是BP边上一点,∠PAC=∠PBA,⊙O是△ABC的外接圆,AD是⊙O的直径,且交BP于点E.
(1)求证:PA是⊙O的切线;
(2)过点C作CF⊥AD,垂足为点F,延长CF交AB于点G,若AG·AB=12,求AC的长.
22.如图,AB为⊙O的直径,C为⊙O上一点,D为的中点.过点D作直线AC的垂线,垂足为E,连接OD.
(1)求证:∠A=∠DOB;
(2)DE与⊙O有怎样的位置关系?请说明理由.
23.如图,AC是⊙O的直径,AB是⊙O的一条弦,AP是⊙O的切线.作BM=AB并与AP交于点M,延长MB交AC于点E,交⊙O于点D,连接AD.
(1)求证:AB=BE;
(2)若⊙O的半径R=5,AB=6,求AD的长.
五、解答题(三)(本大题共2小题,每小题10分,共20分)
24.如图1,在△ABC中,AB=AC,⊙O是△ABC的外接圆,过点C作∠BCD=∠ACB交⊙O于点D,连接AD交BC于点E,延长DC至点F,使CF=AC,连接AF.
(1)求证:ED=EC;
(2)求证:AF是⊙O的切线;
(3)如图2,若点G是△ACD的内心,BC·BE=25,求BG的长.
25.如图,⊙O是△ABC的外接圆,AB是直径,D是AC的中点,直线OD与⊙O相交于E,F两点,P是⊙O外一点,P在直线OD上,连接PA,PC,AF,且满足∠PCA=∠ABC.
(1)求证:PA是⊙O的切线;
(2)证明:EF2=4OD·OP;
(3)若BC=8,tan∠AFP=,求DE的长.
参考答案
一、选择题(本大题10小题,每小题3分,共30分)
1.B
2.A
3.D
4.B
5.C
6.D
7.C
8.B
9.C
10.A
二、填空题(本大题共7小题,每小题4分,共28分)
11.OA>5
12.相切
13.2
14.4
15.2π
16.110°
17.2π-4
三、解答题(一)(本大题共3小题,每小题6分,共18分)
18.证明:∵AB∥CE
∴∠ACE=∠BAC
又∵AC平分∠BAD
∴∠BAC=∠DAC
∴∠ACE=∠CAD
∴=
∴+=+
∴=
∴AD=CE
19.(1)解:∵BC=DC
∴∠CBD=∠CDB=39°
∵∠BAC=∠CDB=39°
∠CAD=∠CBD=39°
∴∠BAD=∠BAC+∠CAD=39°+39°=78°
(2)证明:∵EC=BC
∴∠CEB=∠CBE
而∠CEB=∠2+∠BAE
∠CBE=∠1+∠CBD
∴∠2+∠BAE=∠1+∠CBD
∵∠BAE=∠BDC=∠CBD
∴∠1=∠2
20.(1)证明:∵AB是☉O的直径
∴∠ACB=90°
∴∠CBA+∠CAB=90°
∵∠EAC=∠B
∴∠CAE+∠BAC=90°
即BA⊥AE
∴AE是☉O的切线
(2)解:连接CO
∵AB=6
∴AO=3
∵∠D=60°
∴∠AOC=120°
∴==2π
四、解答题(二)(本大题共3小题,每小题8分,共24分)
21.(1)证明:连接CD
∵AD是☉O的直径
∴∠ACD=90°
∴∠CAD+∠ADC=90°
又∵∠PAC=∠PBA,∠ADC=∠PBA
∴∠PAC=∠ADC
∴∠CAD+∠PAC=90°
∴PA⊥DA
而AD是☉O的直径
∴PA是☉O的切线
(2)解:由(1)知,PA⊥AD
又∵CF⊥AD
∴CF∥PA
∴∠GCA=∠PAC
又∵∠PAC=∠PBA
∴∠GCA=∠PBA
而∠CAG=∠BAC
∴△CAG∽△BAC
∴=,即AC2=AG·AB
∵AG·AB=12
∴AC2=12
∴AC=2
22.(1)证明:连接OC
∵D为的中点
∴=
∴∠DOB=∠BOC
∵∠A=∠BOC
∴∠A=∠DOB.
(2)解:DE与☉O相切.理由如下:
∵∠A=∠DOB
∴AE∥OD
∵DE⊥AE
∴OD⊥DE
又∵点D在☉O上
∴DE与☉O相切
23.(1)证明:∵AP是☉O的切线
∴∠EAM=90°
∴∠BAE+∠MAB=90°,∠AEB+∠AMB=90°.
又∵AB=BM
∴∠MAB=∠AMB
∴∠BAE=∠AEB
∴AB=BE
(2)解:连接BC
∵AC是☉O的直径
∴∠ABC=90°
在Rt△ABC中,AC=10,AB=6
∴BC=8
∵BE=AB=BM
∴EM=12
由(1)知,∠BAE=∠AEB
∴△ABC∽△EAM
∴∠C=∠AME
=,即=
∴AM=
又∵∠D=∠C
∴∠D=∠AMD
∴AD=AM=
五、解答题(三)(本大题共2小题,每小题10分,共20分)
24.(1)证明:∵AB=AC
∴∠ABC=∠ACB
又∵∠ACB=∠BCD,∠ABC=∠ADC
∴∠BCD=∠ADC
∴ED=EC.
(2)证明:如图1,连接OA
∵AB=AC
∴=
∴OA⊥BC
∵CA=CF
∴∠CAF=∠CFA
∴∠ACD=∠CAF+∠CFA=2∠CAF
∵∠ACB=∠BCD
∴∠ACD=2∠ACB
∴∠CAF=∠ACB
∴AF∥BC.
∴OA⊥AF
∴AF为☉O的切线
(3)解:∵∠ABE=∠CBA,∠BAD=∠BCD=∠ACB
∴△ABE∽△CBA
∴=
∴AB2=BC·BE
∵BC·BE=25
∴AB=5
如图2,连接AG
∴∠BAG=∠BAD+∠DAG,∠BGA=∠GAC+∠ACB
∵点G为内心
∴∠DAG=∠GAC
∴∠BAD+∠DAG=∠GAC+∠ACB
∴∠BAG=∠BGA
∴BG=AB=5
25.(1)证明:∵D是弦AC的中点
∴OD⊥AC
∴PD是AC的中垂线
∴PA=PC
∴∠PAC=∠PCA
∵AB是☉O的直径
∴∠ACB=90°
∴∠CAB+∠CBA=90°.
又∵∠PCA=∠ABC
∴∠PCA+∠CAB=90°
∴∠CAB+∠PAC=90°,即AB⊥PA
∴PA是☉O的切线
(2)证明:由(1)知∠ODA=∠OAP=90°
∴Rt△AOD∽Rt△POA
∴=
∴OA2=OD·OP
又OA=EF
∴EF2=OD·OP,即EF2=4OD·OP
(3)解:在Rt△ADF中,设AD=2a,则DF=3a
∵OD=BC=4
∴AO=OF=3a-4.
∵OD2+AD2=AO2,即42+(2a)2=(3a-4)2
解得a=(a=0舍去)
∴DE=OE-OD=3a-8=
4
第三章《圆》单元测试卷
(时间90分钟,满分120分)
班级________
姓名________
学号________
成绩________
一、选择题(本大题10小题,每小题3分,共30分)
1.在△ABC中,∠C=90°,AB=5,BC=4,以A为圆心,以3为半径作图,则点C与⊙A的位置关系为(
)
A.点C在⊙A内
B.点C在⊙A上
C.点C在⊙A外
D.点C在⊙A上或点C在⊙A外
2.下列语句中,正确的有(
)
①相等的圆心角所对的弧相等;②平分弦的直径垂直于弦;③长度相等的两条弧是等弧;④圆是轴对称图形,任何一条直径都是对称轴.
A.0个
B.1个
C.2个
D.3个
3.如图,点A,B,C都在⊙O上,若∠C=35°,则∠AOB的度数为(
)
A.35°
B.55°
C.145°
D.70°
4.如图,在⊙O中,弦AB的长为16cm,圆心O到AB的距离为6
m,则⊙O的半径是(
)
A.6cm
B.10cm
C.8cm
D.20cm
5.如图,⊙O是△ABC的外接圆,弦AC的长为3,sin
B=,则⊙O的半径为(
)
A.4
B.3
C.2
D.
6.如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于D,且CO=CD,则∠PCA=(
)
A.30°
B.45°
C.60°
D.67.5°
题3图
题4图
题5图
题6图
7.扇形的弧长为20πcm,面积为240πcm2,那么扇形的半径是(
)
A.6cm
B.12cm
C.24cm
D.28cm
8.一个圆锥的底面半径是6cm,其侧面展开图为半圆,则圆锥的母线长为(
)
A.9cm
B.12cm
C.15cm
D.18cm
9.⊙O的半径是13,弦AB∥CD,AB=24,CD=10,则AB与CD的距离是(
)
A.7
B.17
C.7或17
D.34
10.如图,在Rt△ABC中,∠A=30°,BC=2,以直角边AC为直径作⊙O交AB于点D,则图中阴影部分的面积是(
)
A.-π
B.-π
C.-
D.-
二、填空题(本大题共7小题,每小题4分,共28分)
11.已知⊙O的半径为5,点A在⊙O外,那么线段OA的取值范围是
.
12.如图,∠O=30°,C为OB上一点,且OC=6,以点C为圆心,半径为3的圆与OA的位置关系是
.
13.如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,则△ABC的内切圆半径r=
.
14.如图,AB是⊙O的直径,点C是⊙O上的一点,若BC=6,AB=10,OD⊥BC于点D,则OD的长为
.
题12图
题13图
题14图
15.若扇形的半径为3,圆心角120°,则此扇形的弧长是
.
16.如图,四边形ABCD内接于⊙O,E为CD延长线上一点.若∠B=110°,则∠ADE的度数为
.
17.如图,在扇形AOB中,∠AOB=90°,正方形CDEF的顶点C是的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2时,则阴影部分的面积为
.
题16图
题17图
三、解答题(一)(本大题共3小题,每小题6分,共18分)
18.如图,点A,B,C,D,E都在⊙O上,AC平分∠BAD,且AB∥CE,求证:AD=CE.
19.如图,四边形ABCD内接于⊙O,点E在对角线AC上,EC=BC=DC.
(1)若∠CBD=39°,求∠BAD的度数;
(2)求证:∠1=∠2.
20.如图,已知AB是⊙O的直径,点C,D在⊙O上,点E在⊙O外,∠EAC=∠B.
(1)求证:直线AE是⊙O的切线;
(2)若∠D=60°,AB=6时,求劣弧的长(结果保留π).
四、解答题(二)(本大题共3小题,每小题8分,共24分)
21.如图,在△ABP中,C是BP边上一点,∠PAC=∠PBA,⊙O是△ABC的外接圆,AD是⊙O的直径,且交BP于点E.
(1)求证:PA是⊙O的切线;
(2)过点C作CF⊥AD,垂足为点F,延长CF交AB于点G,若AG·AB=12,求AC的长.
22.如图,AB为⊙O的直径,C为⊙O上一点,D为的中点.过点D作直线AC的垂线,垂足为E,连接OD.
(1)求证:∠A=∠DOB;
(2)DE与⊙O有怎样的位置关系?请说明理由.
23.如图,AC是⊙O的直径,AB是⊙O的一条弦,AP是⊙O的切线.作BM=AB并与AP交于点M,延长MB交AC于点E,交⊙O于点D,连接AD.
(1)求证:AB=BE;
(2)若⊙O的半径R=5,AB=6,求AD的长.
五、解答题(三)(本大题共2小题,每小题10分,共20分)
24.如图1,在△ABC中,AB=AC,⊙O是△ABC的外接圆,过点C作∠BCD=∠ACB交⊙O于点D,连接AD交BC于点E,延长DC至点F,使CF=AC,连接AF.
(1)求证:ED=EC;
(2)求证:AF是⊙O的切线;
(3)如图2,若点G是△ACD的内心,BC·BE=25,求BG的长.
25.如图,⊙O是△ABC的外接圆,AB是直径,D是AC的中点,直线OD与⊙O相交于E,F两点,P是⊙O外一点,P在直线OD上,连接PA,PC,AF,且满足∠PCA=∠ABC.
(1)求证:PA是⊙O的切线;
(2)证明:EF2=4OD·OP;
(3)若BC=8,tan∠AFP=,求DE的长.
参考答案
一、选择题(本大题10小题,每小题3分,共30分)
1.B
2.A
3.D
4.B
5.C
6.D
7.C
8.B
9.C
10.A
二、填空题(本大题共7小题,每小题4分,共28分)
11.OA>5
12.相切
13.2
14.4
15.2π
16.110°
17.2π-4
三、解答题(一)(本大题共3小题,每小题6分,共18分)
18.证明:∵AB∥CE
∴∠ACE=∠BAC
又∵AC平分∠BAD
∴∠BAC=∠DAC
∴∠ACE=∠CAD
∴=
∴+=+
∴=
∴AD=CE
19.(1)解:∵BC=DC
∴∠CBD=∠CDB=39°
∵∠BAC=∠CDB=39°
∠CAD=∠CBD=39°
∴∠BAD=∠BAC+∠CAD=39°+39°=78°
(2)证明:∵EC=BC
∴∠CEB=∠CBE
而∠CEB=∠2+∠BAE
∠CBE=∠1+∠CBD
∴∠2+∠BAE=∠1+∠CBD
∵∠BAE=∠BDC=∠CBD
∴∠1=∠2
20.(1)证明:∵AB是☉O的直径
∴∠ACB=90°
∴∠CBA+∠CAB=90°
∵∠EAC=∠B
∴∠CAE+∠BAC=90°
即BA⊥AE
∴AE是☉O的切线
(2)解:连接CO
∵AB=6
∴AO=3
∵∠D=60°
∴∠AOC=120°
∴==2π
四、解答题(二)(本大题共3小题,每小题8分,共24分)
21.(1)证明:连接CD
∵AD是☉O的直径
∴∠ACD=90°
∴∠CAD+∠ADC=90°
又∵∠PAC=∠PBA,∠ADC=∠PBA
∴∠PAC=∠ADC
∴∠CAD+∠PAC=90°
∴PA⊥DA
而AD是☉O的直径
∴PA是☉O的切线
(2)解:由(1)知,PA⊥AD
又∵CF⊥AD
∴CF∥PA
∴∠GCA=∠PAC
又∵∠PAC=∠PBA
∴∠GCA=∠PBA
而∠CAG=∠BAC
∴△CAG∽△BAC
∴=,即AC2=AG·AB
∵AG·AB=12
∴AC2=12
∴AC=2
22.(1)证明:连接OC
∵D为的中点
∴=
∴∠DOB=∠BOC
∵∠A=∠BOC
∴∠A=∠DOB.
(2)解:DE与☉O相切.理由如下:
∵∠A=∠DOB
∴AE∥OD
∵DE⊥AE
∴OD⊥DE
又∵点D在☉O上
∴DE与☉O相切
23.(1)证明:∵AP是☉O的切线
∴∠EAM=90°
∴∠BAE+∠MAB=90°,∠AEB+∠AMB=90°.
又∵AB=BM
∴∠MAB=∠AMB
∴∠BAE=∠AEB
∴AB=BE
(2)解:连接BC
∵AC是☉O的直径
∴∠ABC=90°
在Rt△ABC中,AC=10,AB=6
∴BC=8
∵BE=AB=BM
∴EM=12
由(1)知,∠BAE=∠AEB
∴△ABC∽△EAM
∴∠C=∠AME
=,即=
∴AM=
又∵∠D=∠C
∴∠D=∠AMD
∴AD=AM=
五、解答题(三)(本大题共2小题,每小题10分,共20分)
24.(1)证明:∵AB=AC
∴∠ABC=∠ACB
又∵∠ACB=∠BCD,∠ABC=∠ADC
∴∠BCD=∠ADC
∴ED=EC.
(2)证明:如图1,连接OA
∵AB=AC
∴=
∴OA⊥BC
∵CA=CF
∴∠CAF=∠CFA
∴∠ACD=∠CAF+∠CFA=2∠CAF
∵∠ACB=∠BCD
∴∠ACD=2∠ACB
∴∠CAF=∠ACB
∴AF∥BC.
∴OA⊥AF
∴AF为☉O的切线
(3)解:∵∠ABE=∠CBA,∠BAD=∠BCD=∠ACB
∴△ABE∽△CBA
∴=
∴AB2=BC·BE
∵BC·BE=25
∴AB=5
如图2,连接AG
∴∠BAG=∠BAD+∠DAG,∠BGA=∠GAC+∠ACB
∵点G为内心
∴∠DAG=∠GAC
∴∠BAD+∠DAG=∠GAC+∠ACB
∴∠BAG=∠BGA
∴BG=AB=5
25.(1)证明:∵D是弦AC的中点
∴OD⊥AC
∴PD是AC的中垂线
∴PA=PC
∴∠PAC=∠PCA
∵AB是☉O的直径
∴∠ACB=90°
∴∠CAB+∠CBA=90°.
又∵∠PCA=∠ABC
∴∠PCA+∠CAB=90°
∴∠CAB+∠PAC=90°,即AB⊥PA
∴PA是☉O的切线
(2)证明:由(1)知∠ODA=∠OAP=90°
∴Rt△AOD∽Rt△POA
∴=
∴OA2=OD·OP
又OA=EF
∴EF2=OD·OP,即EF2=4OD·OP
(3)解:在Rt△ADF中,设AD=2a,则DF=3a
∵OD=BC=4
∴AO=OF=3a-4.
∵OD2+AD2=AO2,即42+(2a)2=(3a-4)2
解得a=(a=0舍去)
∴DE=OE-OD=3a-8=
4
