2020=2021学年八年级数学北师大版下册第三章《图形的平移与旋转》单元测试卷(word含答案)
文档属性
| 名称 | 2020=2021学年八年级数学北师大版下册第三章《图形的平移与旋转》单元测试卷(word含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 225.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-18 20:53:51 | ||
图片预览

文档简介
北师版八年级数学?下册
第三章《图形的平移与旋转》单元测试卷
(时间90分钟,满分120分)
班级________
姓名________
学号________
成绩________
一、选择题(本大题10小题,每小题3分,共30分)
1.如图,所给图形中是中心对称图形但不是轴对称图形的是(
)
2.下面每组图形中,左面的图形平移后可以得到右面的图形的是(
)
3.下列说法正确的是(
)
A.在平移和旋转图形中,对应角相等,对应线段相等且平行
B.平移和旋转的共同点是不改变图形的形状和大小
C.图形可以向某一方向平移一定距离,也可以向某一方向旋转一定距离
D.由平移得到的图形也一定可由旋转得到
4.把点M(-2,1)向右平移3个单位长度,再向下平移2个单位长度后得到点N,则点N的坐标为(
)
A.(-4,4)
B.(-5,3)
C.(1,-1)
D.(-5,-1)
5.将数字“6”旋转180°,得到数字“9”;将数字“9”旋转180°,得到数字“6”.现将数字“96”旋转180°,得到的数字是(
)
A.96
B.69
C.66
D.99
6.如图,将△ABC沿BC方向平移1个单位长度得到△DEF,如果四边形ABFD的周长为12,则△ABC的周长为(
)
A.8
B.10
C.12
D.14
7.如图,在△ABC中,∠CAB=65°,在同一平面内,将△ABC绕点A旋转到△AB'C'的位置,使得CC'∥AB,则∠BAB'的度数为(
)
A.25°
B.30°
C.50°
D.55°
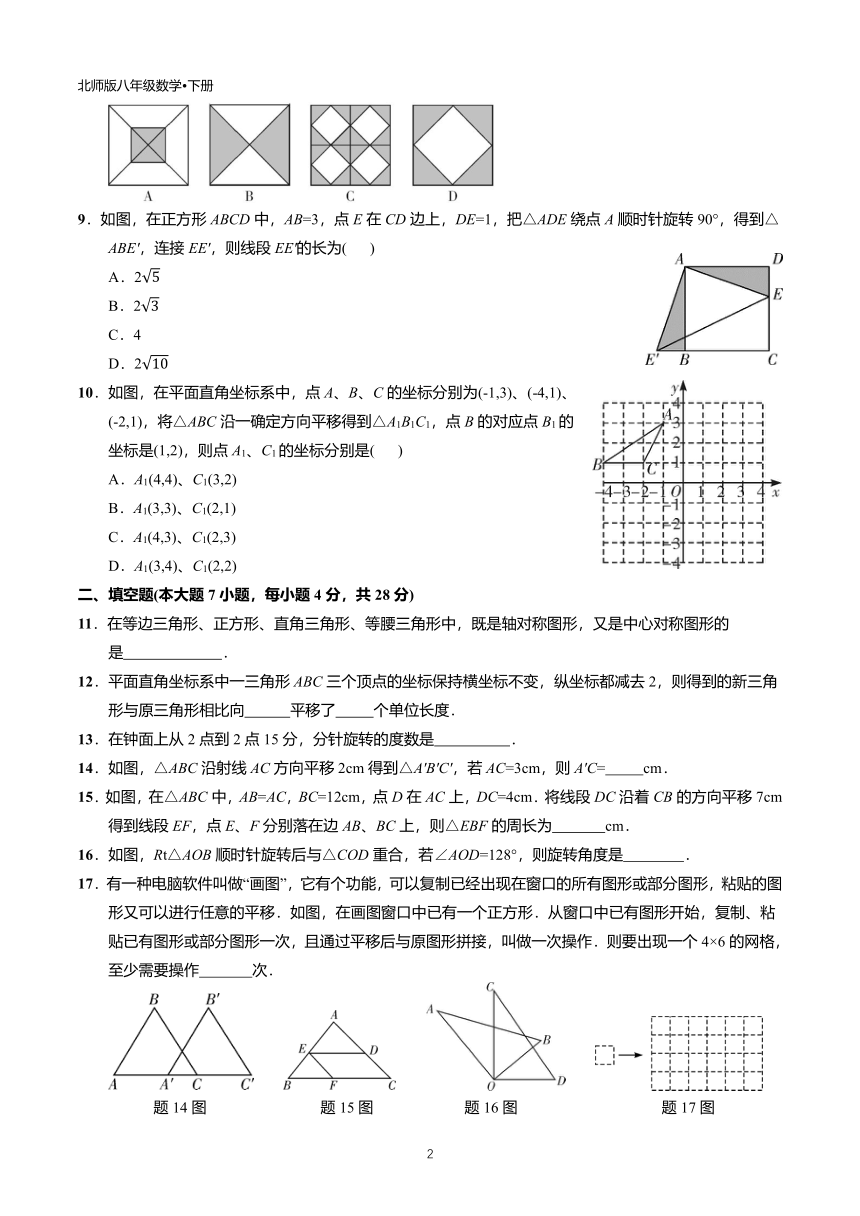
8.下列四个图案中,既可用旋转来分析整个图案的形成过程,又可用平移来分析整个图案的形成过程的图案是(
)
9.如图,在正方形ABCD中,AB=3,点E在CD边上,DE=1,把△ADE绕点A顺时针旋转90°,得到△ABE',连接EE',则线段EE'的长为(
)
A.2
B.2
C.4
D.2
10.如图,在平面直角坐标系中,点A、B、C的坐标分别为(-1,3)、(-4,1)、(-2,1),将△ABC沿一确定方向平移得到△A1B1C1,点B的对应点B1的坐标是(1,2),则点A1、C1的坐标分别是(
)
A.A1(4,4)、C1(3,2)
B.A1(3,3)、C1(2,1)
C.A1(4,3)、C1(2,3)
D.A1(3,4)、C1(2,2)
二、填空题(本大题7小题,每小题4分,共28分)
11.在等边三角形、正方形、直角三角形、等腰三角形中,既是轴对称图形,又是中心对称图形的是
.
12.平面直角坐标系中一三角形ABC三个顶点的坐标保持横坐标不变,纵坐标都减去2,则得到的新三角形与原三角形相比向
平移了
个单位长度.
13.在钟面上从2点到2点15分,分针旋转的度数是
.
14.如图,△ABC沿射线AC方向平移2cm得到△A'B'C',若AC=3cm,则A'C=
cm.
15.如图,在△ABC中,AB=AC,BC=12cm,点D在AC上,DC=4cm.将线段DC沿着CB的方向平移7cm得到线段EF,点E、F分别落在边AB、BC上,则△EBF的周长为
cm.
16.如图,Rt△AOB顺时针旋转后与△COD重合,若∠AOD=128°,则旋转角度是
.
17.有一种电脑软件叫做“画图”,它有个功能,可以复制已经出现在窗口的所有图形或部分图形,粘贴的图形又可以进行任意的平移.如图,在画图窗口中已有一个正方形.从窗口中已有图形开始,复制、粘贴已有图形或部分图形一次,且通过平移后与原图形拼接,叫做一次操作.则要出现一个4×6的网格,至少需要操作
次.
题14图
题15图
题16图
题17图
三、解答题(一)(本大题3小题,每小题6分,共18分)
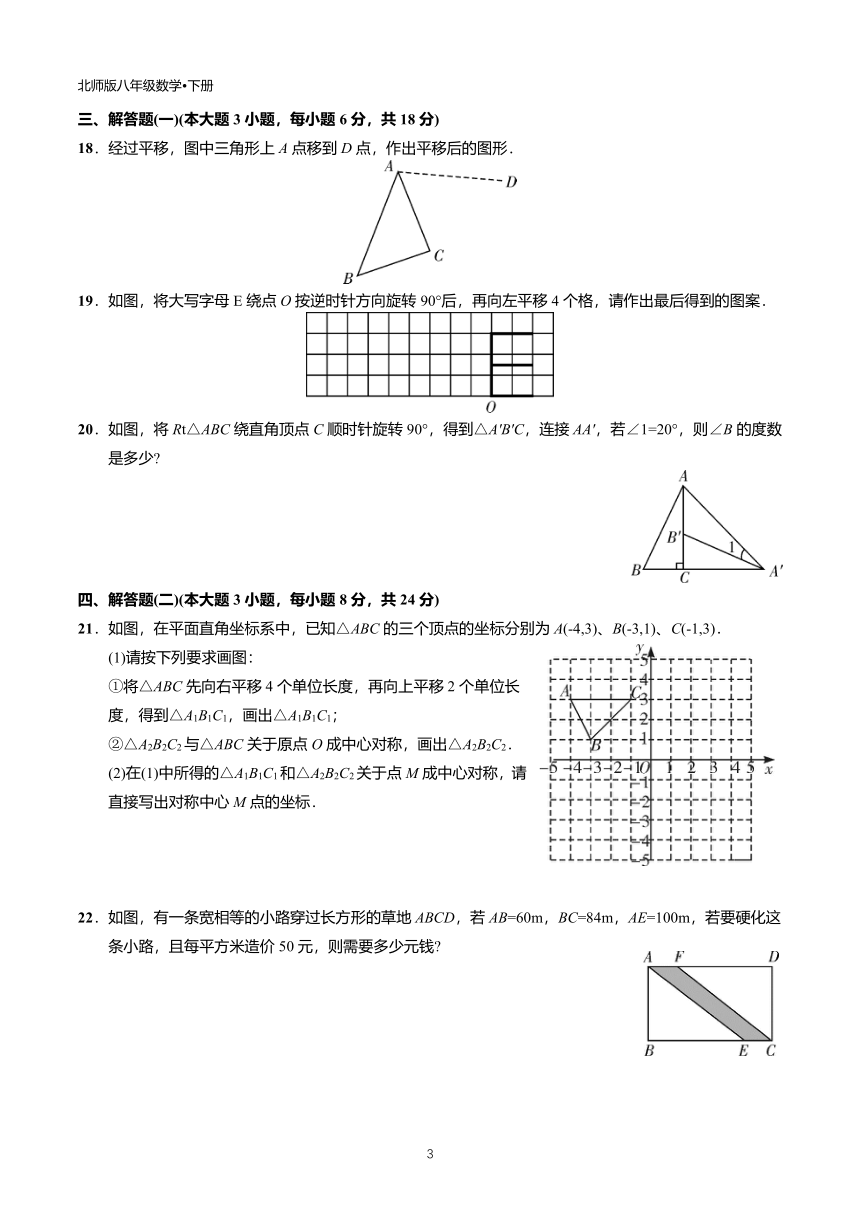
18.经过平移,图中三角形上A点移到D点,作出平移后的图形.
19.如图,将大写字母E绕点O按逆时针方向旋转90°后,再向左平移4个格,请作出最后得到的图案.
20.如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A'B'C,连接AA',若∠1=20°,则∠B的度数是多少?
四、解答题(二)(本大题3小题,每小题8分,共24分)
21.如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-4,3)、B(-3,1)、C(-1,3).
(1)请按下列要求画图:
①将△ABC先向右平移4个单位长度,再向上平移2个单位长度,得到△A1B1C1,画出△A1B1C1;
②△A2B2C2与△ABC关于原点O成中心对称,画出△A2B2C2.
(2)在(1)中所得的△A1B1C1和△A2B2C2关于点M成中心对称,请直接写出对称中心M点的坐标.
22.如图,有一条宽相等的小路穿过长方形的草地ABCD,若AB=60m,BC=84m,AE=100m,若要硬化这条小路,且每平方米造价50元,则需要多少元钱?
23.如图,在四边形ABCD中,∠BAD=∠C=90°,AB=AD,AE⊥BC于E,△BEA旋转后能与△DFA重合.
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)如果点A是旋转中心,那么点B经过旋转后,点B旋转到什么位置?
五、解答题(三)(本大题2小题,每小题10分,共20分)
24.如图,已知△ABC是等腰直角三角形,BC为斜边,将△ABP绕点A逆时针旋转后,能与△ACP'重合.
(1)若∠ABP=20°,求∠CAP'的度数;
(2)若AP=3,求PP'的长.
25.如图,△ABC是边长为3的等边三角形,将△ABC沿直线BC向右平移,使点B与点C重合,得到△DCE,连接BD,交AC于F.
(1)求∠BDC的大小;
(2)求线段BD的长;
(3)猜想AC与BD的位置关系,并证明你的结论.
参考答案
一、选择题(本大题10小题,每小题3分,共30分)
1.C
2.D
3.B
4.C
5.A
6.B
7.C
8.C
9.A
10.A
二、填空题(本大题7小题,每小题4分,共28分)
11.正方形
12.下
2
13.90°
14.1
15.13
16.38°
17.5
三、解答题(一)(本大题3小题,每小题6分,共18分)
18.解:
19.解:
20.解:∵Rt△A'B'C是由Rt△ABC顺时针旋转90°得到
∴Rt△A'B'C≌Rt△ABC
∴AC=A'C,∠ACA'=90°
∴△ACA'为等腰直角三角形
∴∠AA'C=45°
∵∠1=20°
∴∠B'A'C=25°
∴∠A'B'C=90°-25°=65°
∴∠B=∠A'B'C=65°
四、解答题(二)(本大题3小题,每小题8分,共24分)
21.解:(1)①△A1B1C1如图所示;
②△A2B2C2如图所示.
(2)连接B1B2、C1C2,得到对称中心M的坐标为(2,1)
22.解:∵四边形ABCD是长方形
∴∠B=90°
∵∠B=90°,AB=60m,AE=100m
∴根据勾股定理可求得BE=80m
∵路等宽,BC=84m
∴AF平行且等于EC,AF可以看成由EC平移得到
∴AF=EC=4m
∴S四边形AECF=EC×AB=240m2
∵每平方米造价为50元
∴需要240×50=12000元
23.解:(1)点A
(2)90°
(3)点D
五、解答题(三)(本大题2小题,每小题10分,共20分)
24.解:(1)∵△ABC是等腰直角三角形,BC是斜边,将△ABP绕点A按逆时针方向旋转后,能与△ACP'重合
∴∠PAP'=∠BAC=90°,∠CAP'=∠BAP,PA=P'A
∴∠APP'=45°
∵∠ABP=20°
∴∠BAP=∠APP'-∠ABP=45°-20°=25°
∴∠CAP'=25°
(2)∵△ACP'是由△ABP绕点A逆时针旋转后得到的
∴△ACP'≌△ABP
∴AP=AP',∠BAP=∠CAP'
∵∠BAC=90°
∴∠PAP'=90°
∵AP=3
∴AP'=3
∴PP'==3
25.解:(1)∵△ABC与△DCE为等边三角形,且△DCE由△ABC平移得到
∴∠DCE=60°,BC=CD
∴∠BDC=∠DCE=×60°=30°
(2)由(1)得∠BDE=90°,在Rt△BED中,∵BE=6,DE=3
∴BD===3
(3)AC⊥BD.证明如下:
∵由(1)得BC=CD,∠CBF=∠BDC=30°,∠ACB=60°
∴∠BFC=180°-∠ACB-∠CBF=180°-60°-30°=90°
∴BD⊥AC
6
第三章《图形的平移与旋转》单元测试卷
(时间90分钟,满分120分)
班级________
姓名________
学号________
成绩________
一、选择题(本大题10小题,每小题3分,共30分)
1.如图,所给图形中是中心对称图形但不是轴对称图形的是(
)
2.下面每组图形中,左面的图形平移后可以得到右面的图形的是(
)
3.下列说法正确的是(
)
A.在平移和旋转图形中,对应角相等,对应线段相等且平行
B.平移和旋转的共同点是不改变图形的形状和大小
C.图形可以向某一方向平移一定距离,也可以向某一方向旋转一定距离
D.由平移得到的图形也一定可由旋转得到
4.把点M(-2,1)向右平移3个单位长度,再向下平移2个单位长度后得到点N,则点N的坐标为(
)
A.(-4,4)
B.(-5,3)
C.(1,-1)
D.(-5,-1)
5.将数字“6”旋转180°,得到数字“9”;将数字“9”旋转180°,得到数字“6”.现将数字“96”旋转180°,得到的数字是(
)
A.96
B.69
C.66
D.99
6.如图,将△ABC沿BC方向平移1个单位长度得到△DEF,如果四边形ABFD的周长为12,则△ABC的周长为(
)
A.8
B.10
C.12
D.14
7.如图,在△ABC中,∠CAB=65°,在同一平面内,将△ABC绕点A旋转到△AB'C'的位置,使得CC'∥AB,则∠BAB'的度数为(
)
A.25°
B.30°
C.50°
D.55°
8.下列四个图案中,既可用旋转来分析整个图案的形成过程,又可用平移来分析整个图案的形成过程的图案是(
)
9.如图,在正方形ABCD中,AB=3,点E在CD边上,DE=1,把△ADE绕点A顺时针旋转90°,得到△ABE',连接EE',则线段EE'的长为(
)
A.2
B.2
C.4
D.2
10.如图,在平面直角坐标系中,点A、B、C的坐标分别为(-1,3)、(-4,1)、(-2,1),将△ABC沿一确定方向平移得到△A1B1C1,点B的对应点B1的坐标是(1,2),则点A1、C1的坐标分别是(
)
A.A1(4,4)、C1(3,2)
B.A1(3,3)、C1(2,1)
C.A1(4,3)、C1(2,3)
D.A1(3,4)、C1(2,2)
二、填空题(本大题7小题,每小题4分,共28分)
11.在等边三角形、正方形、直角三角形、等腰三角形中,既是轴对称图形,又是中心对称图形的是
.
12.平面直角坐标系中一三角形ABC三个顶点的坐标保持横坐标不变,纵坐标都减去2,则得到的新三角形与原三角形相比向
平移了
个单位长度.
13.在钟面上从2点到2点15分,分针旋转的度数是
.
14.如图,△ABC沿射线AC方向平移2cm得到△A'B'C',若AC=3cm,则A'C=
cm.
15.如图,在△ABC中,AB=AC,BC=12cm,点D在AC上,DC=4cm.将线段DC沿着CB的方向平移7cm得到线段EF,点E、F分别落在边AB、BC上,则△EBF的周长为
cm.
16.如图,Rt△AOB顺时针旋转后与△COD重合,若∠AOD=128°,则旋转角度是
.
17.有一种电脑软件叫做“画图”,它有个功能,可以复制已经出现在窗口的所有图形或部分图形,粘贴的图形又可以进行任意的平移.如图,在画图窗口中已有一个正方形.从窗口中已有图形开始,复制、粘贴已有图形或部分图形一次,且通过平移后与原图形拼接,叫做一次操作.则要出现一个4×6的网格,至少需要操作
次.
题14图
题15图
题16图
题17图
三、解答题(一)(本大题3小题,每小题6分,共18分)
18.经过平移,图中三角形上A点移到D点,作出平移后的图形.
19.如图,将大写字母E绕点O按逆时针方向旋转90°后,再向左平移4个格,请作出最后得到的图案.
20.如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A'B'C,连接AA',若∠1=20°,则∠B的度数是多少?
四、解答题(二)(本大题3小题,每小题8分,共24分)
21.如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-4,3)、B(-3,1)、C(-1,3).
(1)请按下列要求画图:
①将△ABC先向右平移4个单位长度,再向上平移2个单位长度,得到△A1B1C1,画出△A1B1C1;
②△A2B2C2与△ABC关于原点O成中心对称,画出△A2B2C2.
(2)在(1)中所得的△A1B1C1和△A2B2C2关于点M成中心对称,请直接写出对称中心M点的坐标.
22.如图,有一条宽相等的小路穿过长方形的草地ABCD,若AB=60m,BC=84m,AE=100m,若要硬化这条小路,且每平方米造价50元,则需要多少元钱?
23.如图,在四边形ABCD中,∠BAD=∠C=90°,AB=AD,AE⊥BC于E,△BEA旋转后能与△DFA重合.
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)如果点A是旋转中心,那么点B经过旋转后,点B旋转到什么位置?
五、解答题(三)(本大题2小题,每小题10分,共20分)
24.如图,已知△ABC是等腰直角三角形,BC为斜边,将△ABP绕点A逆时针旋转后,能与△ACP'重合.
(1)若∠ABP=20°,求∠CAP'的度数;
(2)若AP=3,求PP'的长.
25.如图,△ABC是边长为3的等边三角形,将△ABC沿直线BC向右平移,使点B与点C重合,得到△DCE,连接BD,交AC于F.
(1)求∠BDC的大小;
(2)求线段BD的长;
(3)猜想AC与BD的位置关系,并证明你的结论.
参考答案
一、选择题(本大题10小题,每小题3分,共30分)
1.C
2.D
3.B
4.C
5.A
6.B
7.C
8.C
9.A
10.A
二、填空题(本大题7小题,每小题4分,共28分)
11.正方形
12.下
2
13.90°
14.1
15.13
16.38°
17.5
三、解答题(一)(本大题3小题,每小题6分,共18分)
18.解:
19.解:
20.解:∵Rt△A'B'C是由Rt△ABC顺时针旋转90°得到
∴Rt△A'B'C≌Rt△ABC
∴AC=A'C,∠ACA'=90°
∴△ACA'为等腰直角三角形
∴∠AA'C=45°
∵∠1=20°
∴∠B'A'C=25°
∴∠A'B'C=90°-25°=65°
∴∠B=∠A'B'C=65°
四、解答题(二)(本大题3小题,每小题8分,共24分)
21.解:(1)①△A1B1C1如图所示;
②△A2B2C2如图所示.
(2)连接B1B2、C1C2,得到对称中心M的坐标为(2,1)
22.解:∵四边形ABCD是长方形
∴∠B=90°
∵∠B=90°,AB=60m,AE=100m
∴根据勾股定理可求得BE=80m
∵路等宽,BC=84m
∴AF平行且等于EC,AF可以看成由EC平移得到
∴AF=EC=4m
∴S四边形AECF=EC×AB=240m2
∵每平方米造价为50元
∴需要240×50=12000元
23.解:(1)点A
(2)90°
(3)点D
五、解答题(三)(本大题2小题,每小题10分,共20分)
24.解:(1)∵△ABC是等腰直角三角形,BC是斜边,将△ABP绕点A按逆时针方向旋转后,能与△ACP'重合
∴∠PAP'=∠BAC=90°,∠CAP'=∠BAP,PA=P'A
∴∠APP'=45°
∵∠ABP=20°
∴∠BAP=∠APP'-∠ABP=45°-20°=25°
∴∠CAP'=25°
(2)∵△ACP'是由△ABP绕点A逆时针旋转后得到的
∴△ACP'≌△ABP
∴AP=AP',∠BAP=∠CAP'
∵∠BAC=90°
∴∠PAP'=90°
∵AP=3
∴AP'=3
∴PP'==3
25.解:(1)∵△ABC与△DCE为等边三角形,且△DCE由△ABC平移得到
∴∠DCE=60°,BC=CD
∴∠BDC=∠DCE=×60°=30°
(2)由(1)得∠BDE=90°,在Rt△BED中,∵BE=6,DE=3
∴BD===3
(3)AC⊥BD.证明如下:
∵由(1)得BC=CD,∠CBF=∠BDC=30°,∠ACB=60°
∴∠BFC=180°-∠ACB-∠CBF=180°-60°-30°=90°
∴BD⊥AC
6
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
