3.3 中心对称同步练习（含解析）

3.3中心对称
姓名：__________________ 班级：______________ 得分：_________________
注意事项：
本试卷满分100分，试题共24题，选择10道、填空8道、解答6道．答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置．
一、选择题（本大题共10小题，每小题3分，共30分）在每小题所给出的四个选项中，只有一项是符合题目要求的．
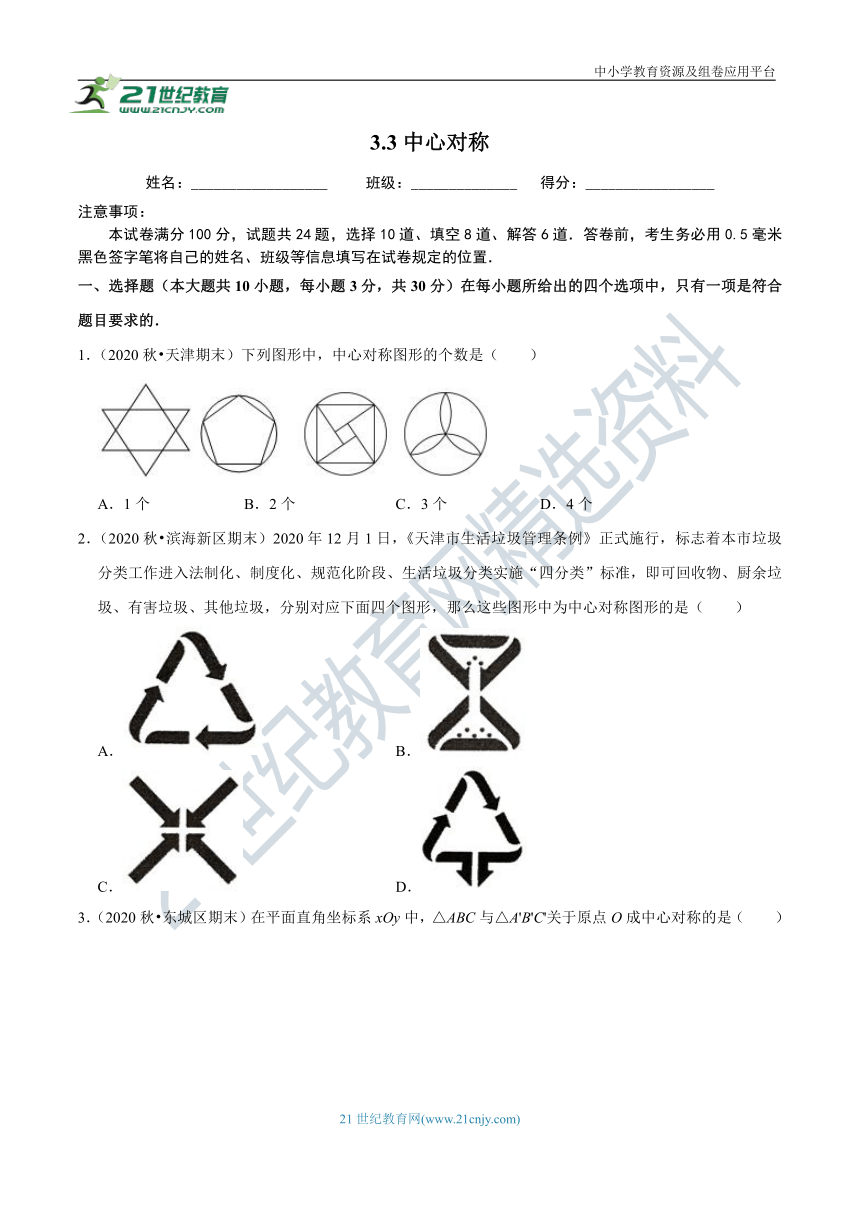
1．（2020秋?天津期末）下列图形中，中心对称图形的个数是（　　）
A．1个 B．2个 C．3个 D．4个
2．（2020秋?滨海新区期末）2020年12月1日，《天津市生活垃圾管理条例》正式施行，标志着本市垃圾分类工作进入法制化、制度化、规范化阶段、生活垃圾分类实施“四分类”标准，即可回收物、厨余垃圾、有害垃圾、其他垃圾，分别对应下面四个图形，那么这些图形中为中心对称图形的是（　　）
A． B．
C． D．
3．（2020秋?东城区期末）在平面直角坐标系xOy中，△ABC与△A'B'C'关于原点O成中心对称的是（　　）
A． B．
C． D．
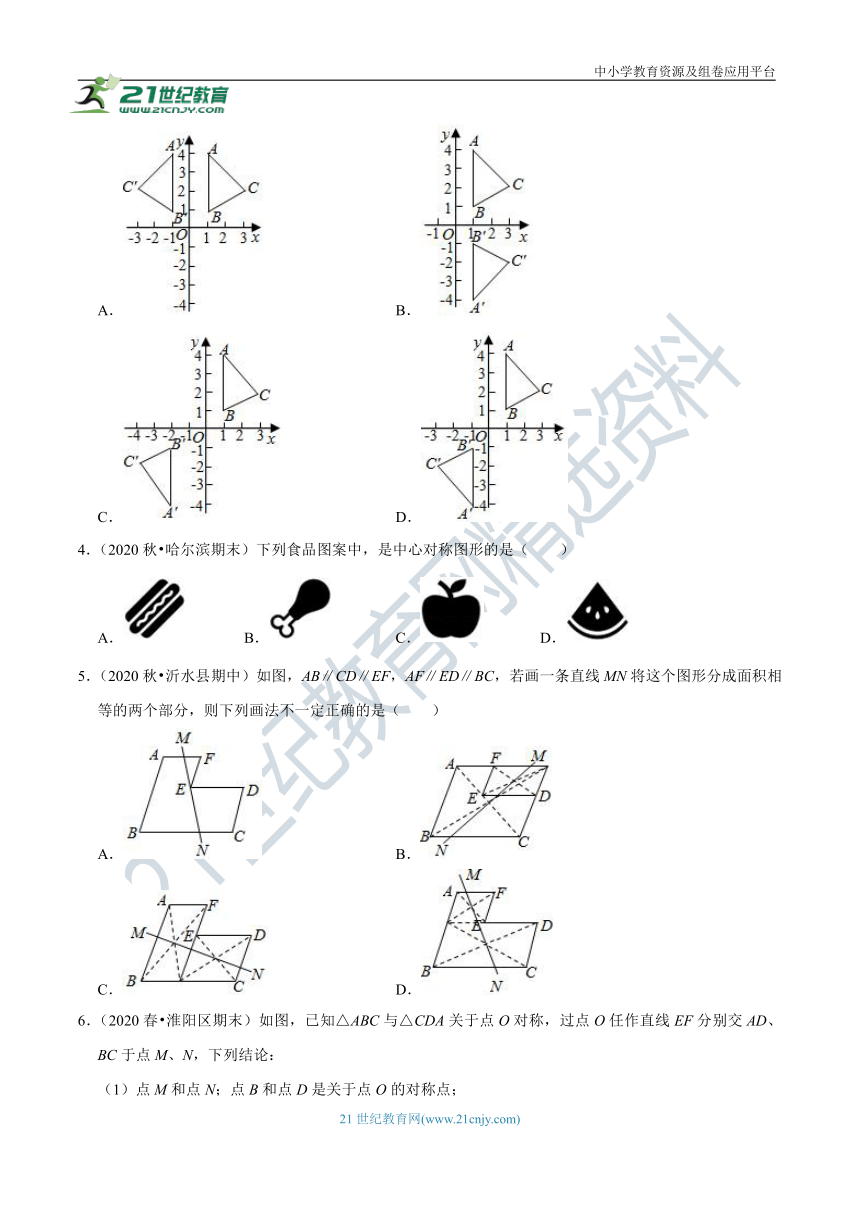
4．（2020秋?哈尔滨期末）下列食品图案中，是中心对称图形的是（　　）
A． B． C． D．
5．（2020秋?沂水县期中）如图，AB∥CD∥EF，AF∥ED∥BC，若画一条直线MN将这个图形分成面积相等的两个部分，则下列画法不一定正确的是（　　）
A． B．
C． D．
6．（2020春?淮阳区期末）如图，已知△ABC与△CDA关于点O对称，过点O任作直线EF分别交AD、BC于点M、N，下列结论：
（1）点M和点N；点B和点D是关于点O的对称点；
（2）直线BD必经过点O；
（3）四边形ABCD是中心对称图形；
（4）四边形DMOC和四边形BNOA的面积相等；
（5）△AOM和△CON成中心对称．
其中，正确的有（　　）
A．2 个 B．3个 C．5个 D．1个
7．（2020春?新昌县期末）如图，在矩形ABCD中，把∠A沿DF折叠，点A恰好落在矩形的对称中心E处，则∠ADF的度数为（　　）
A．15° B．20° C．25° D．30°
8．（2020春?无锡期中）在平面直角坐标系xOy中，点A（4，3），点B为x轴正半轴上一点，将△AOB绕其一顶点旋转180°，连接其余四个顶点得到一个四边形，若该四边形是一个轴对称图形，则满足条件的点有（　　）
A．5个 B．4个 C．3个 D．2个
9．（2019秋?东城区校级期中）如图，⊙M的半径为2，圆心M的坐标为（3，4），点P是⊙M上的任意一点，PA⊥PB，且PA、PB与x轴分别交于A、B两点，若点A、点B关于原点O对称，则AB的最小值为（　　）
A．3 B．4 C．5 D．6
10．（2020春?南岸区期末）如图，在平面直角坐标系内，Rt△ABC的点A在第一象限，点B与点A关于原点对称，∠C＝90°．AC与x轴交于点D，点E在x轴上，CD＝2AD．若AD平分∠OAE，△ADE的面积为1，则△ABC的面积为（　　）
A．6 B．9 C．12 D．15
二、填空题（本大题共8小题，每小题3分，共24分）请把答案直接填写在横线上
11．（2020秋?潮阳区期末）在平面直角坐标系中，A（2，﹣3）与点B关于原点对称，则点B的坐标是　 　．
12．（2020秋?西宁期末）坐标平面内的点P（m，﹣2）与点Q（3，n）关于原点对称，则m+n＝　 　．
13．（2020秋?陆川县期中）如图，将△ABC绕点C（0，﹣1）旋转180°得到△A′B′C，若点A的坐标为（﹣4，﹣3），则点A′的坐标为　 　．
14．（2020春?舞钢市期末）如图，△ABC和△DEC关于点C成中心对称，若AC＝1，AB＝2，∠BAC＝90°，则AE的长是　 　．
15．（2018秋?芝罘区期末）如图，把一个如图所示的“俄罗斯方块”图案放到平面直角坐标系中，每个小正方形的边长都是1个单位长度，经过原点的一条直线l将这个图案分成面积相等的两部分，则该直线的函数关系式为　 　．
16．（2018春?镇平县期末）若△ABC与△DEF关于点O成中心对称，且A、B、C的对称点分别为D、E、F，若AB＝5，AC＝3，则EF的范围是　 　．
17．（2020春?万州区期末）如图，一副直角三角板△ABC和△DEF，∠F＝30°，将△ABC和△DEF放置如图2的位置，点B、D、C、F在同一直线上，点A在DE上，△ABC固定不动，当△EDF绕点D逆时针旋转至180°的过程中（不含180°），当旋转角为　 　时，EF与△ABC的边垂直．
18．（2020春?商水县期末）图1和图2中所有的小正方形都全等，将图1的正方形放在图2中①②③④的某一位置，使它与原来7个小正方形组成的图形是中心对称图形，这个位置是　 　．
三、解答题（本大题共6小题，共46分．解答时应写出文字说明、证明过程或演算步骤）
19．（2019春?秦淮区期末）如图，是5个全等的小正方形组成的图案，请用不同的两种方法分别在两幅图中各添加1个正方形，使整个图案称为中心对称图形．
20．（2018秋?槐荫区期末）如图，方格纸中有三个点A，B，C，要求作一个四边形使这三个点在这个四边形的边（包括顶点）上，且四边形的顶点在方格的顶点上．
（1）在甲图中作出的四边形是中心对称图形但不是轴对称图形；
（2）在乙图中作出的四边形是轴对称图形但不是中心对称图形；
（3）在丙图中作出的四边形既是轴对称图形又是中心对称图形．
21．（2019秋?吉安期中）在平面直角坐标系xOy中，△ABC的位置如图所示．
（1）顶点A关于x轴对称的点A′的坐标（　 　，　 　），顶点B的坐标（　 　，　 　），顶点C关于原点对称的点C′的坐标（　 　，　 　）．
（2）△ABC的面积为　 　．
22．（2016秋?松山区期中）当m为何值时：
（1）点A（2，3m）关于原点的对称点在第三象限；
（2）点B（3m﹣1，0.5m+2）到x轴的距离等于它到y轴距离的一半？
23．（2019春?玉田县期中）如图，我们给中国象棋棋盘建立一个平面直角坐标系（每个小正方形的边长均为1），根据象棋中“马”走“日”的规定，若“马”的位置在图中的点P．
（1）写出下一步“马”可能到达的点的坐标为　 　（写出所有可能的点的坐标）；
（2）顺次连接 （1）中的所有点，得到的图形是　 　图形（填“中心对称”、“旋转对称”或“轴对称”）；
（3）将（2）中得到的图形的各顶点的坐标都乘以1.5，请在平面直角坐标系中画出变化后的图形，并与原图形比较，形状和大小有怎样的变化？
24．（2019秋?沙坪坝区校级期中）在学习函数的过程中，我们经历了“确定函数的表达式﹣﹣利用函数图象研究其性质﹣﹣运用函数解决问题”的学习过程，根据你所经历的学习过程，现在来解决下面的问题：在函数y＝ax3﹣bx+2中，当x＝﹣1时，y＝4；当x＝﹣2时 y＝0．
（1）根据已知条件可知这个函数的表达式　 　．
（2）根据已描出的部分点，画出该函数图象．
（3）观察所画图象，回答下列问题：
①该图象关于点　 　成中心对称；
②当x取何值时，y随着x的增大而减小；
③若直线y＝c与该图象有3个交点，直接写出c的取值范围．
答案
一、选择题（本大题共10小题，每小题3分，共30分）在每小题所给出的四个选项中，只有一项是符合题目要求的．
1．【解析】根据中心对称图形的概念，知第1，3个图形都是中心对称图形，
故选：B．
2．【解析】A、不是中心对称图形，故本选项不合题意；
B、不是中心对称图形，故本选项不合题意；
C、是中心对称图形，故本选项符合题意；
D、不是中心对称图形，故本选项不合题意．
故选：C．
3．【解析】A、△ABC与△A'B'C'关于y轴对称，所以A选项不符合题意；
B、△ABC与△A'B'C'关于x轴对称，所以B选项不符合题意；
C、△ABC与△A'B'C'关于（-12，0）对称，所以C选项不符合题意；
D、△ABC与△A'B'C'关于原点对称，所以D选项符合题意；
故选：D．
4．【解析】A、是中心对称图形，故此选项符合题意；
B、不是中心对称图形，故此选项不合题意；
C、不是中心对称图形，故此选项不合题意；
D、不是中心对称图形，故此选项不合题意．
故选：A．
5．【解析】因为平行四边形是中心对称图形，
所以直线经过两个平行四边形的对角线的交点即可，
观察图象可知，选项B，C，D符合题意，
故选：A．
6．【解析】△ABC与△CDA关于点O对称，则AB＝CD、AD＝BC，所以四边形ABCD是平行四边形，
因此点O就是?ABCD的对称中心，则有：
（1）点M和点N；B和D是关于中心O的对称点，正确；
（2）直线BD必经过点O，正确；
（3）四边形ABCD是中心对称图形，正确；
（4）四边形DMOC与四边形BNOA的面积必相等，正确；
（5）△AOM与△CON成中心对称，正确；
其中正确的个数为5个，
故选：C．
7．【解析】如图，连接AE，
∵把∠A沿DF折叠，点A恰好落在矩形的对称中心E处，
∴AD＝ED＝AE，∠ADF＝∠EDF=12∠ADE，
∴△DAE是等边三角形，
∴∠ADE＝60°，
∴∠ADF＝30°，
故选：D．
8．【解析】观察图象可知，满足条件的点B有5个．
故选：A．
9．【解析】连接OP，
∵PA⊥PB，
∴∠APB＝90°，
∵AO＝BO，
∴AB＝2PO，
若要使AB取得最小值，则PO需取得最小值，
连接OM，交⊙M于点P′，当点P位于P′位置时，OP′取得最小值，
过点M作MQ⊥x轴于点Q，
则OQ＝3、MQ＝4，
∴OM＝5，
又∵MP′＝2，
∴OP′＝3，
∴AB＝2OP′＝6，
故选：D．
10．【解析】如图，取OA的中点F，连接DF、OC，
由点B与点A关于原点对称．可得OA＝OB，
又∵△ABC是直角三角形，
∴OC＝OA，
∴∠OCA＝∠OAC，
∵AD平分∠OAE，
∴∠OAD＝∠EAD，
∴∠OCA＝∠EAD，
∴OC∥AE，
∵CD＝2AD，
∴OC＝2AE，
∵F是OA的中点，
∴OA＝2AF，
∴AF＝AE，
∴△ADF≌△ADE（ASA），
∴S△AOD＝2S△ADE＝2．
∴S△AOC＝3S△AOD＝6，
∴S△ABC＝2S△AOC＝12．
故选：C．
二、填空题（本大题共8小题，每小题3分，共24分）请把答案直接填写在横线上
11．【解析】A（2，﹣3）与点B关于原点对称，则点B的坐标是（﹣2，3），
故答案为：（﹣2，3）．
12．【解析】∵点P（m，﹣2）与点Q（3，n）关于原点对称，
∴m＝﹣3，n＝2，
所以，m+n＝﹣3+2＝﹣1．
故答案为：﹣1．
13．【解析】作A′E⊥y轴于点E，AD⊥y轴于点D，则∠A′EC＝∠ADC，
∵∠A′CE＝∠ACD，AC＝A′C，
∴△A′EC≌△ADC（AAS），
∴AD＝A′E＝4，CE＝CD，
∵OD＝3，OC＝1，
∴CD＝2，
∴CE＝2，
∴OE＝1，
∴点A′的坐标为（4，1）．
故答案为：（4，1）．
14．【解析】∵△DEC与△ABC关于点C成中心对称，
∴△ABC≌△DEC，
∴AB＝DE＝2，AC＝DC＝1，∠D＝∠BAC＝90°，
∴AD＝2，
∵∠D＝90°，
∴AE=AD2+DE2=22，
故答案为22．
15．【解析】设直线l与俄罗斯方块交于点A．
∵直线l将这个图案分成面积相等的两部分，
∴S△OAB=12×3=32，
即12OB?AB=32，
12×2×AB=32，
AB=32，
∴A（2，32），
设直线l解析式y＝kx，
将A（2，32）代入，得32=2k，
解得k=34，
∴该直线的函数关系式为y=34x，
故答案为y=34x．
16．【解析】∵△ABC与△DEF关于点O成中心对称，且A、B、C的对称点分别为D、E、F，AB＝5，AC＝3，
∴DE＝5，DF＝3
∴EF的取值范围为：2＜EF＜8
故答案为：2＜EF＜8
17．【解析】如图1所示，
当AC⊥EF时，
∵∠F＝30°，
∴∠GHF＝60°，
∴∠DHC＝60°，
∵∠HCD＝45°，
∴∠FDC＝75°，
∴当旋转角为75°时，EF⊥AC；
如图2所示，
当BC⊥EF时，
∵∠F＝30°，
∴∠GDF＝60°，
∴∠FDC＝120°，
∴当旋转角为120°时，EF⊥BC．
如图3所示，
当AB⊥EF时，
∵∠F＝30°，
∴∠GHF＝60°，
∴∠AHD＝60°，
∵∠BAD＝45°，
∴∠ADH＝75°，
∴∠FDC＝75°+90°＝165°，
∴当旋转角为165°时，EF⊥AB．
综上，当旋转角为75°或120°或165°时，EF与△ABC的边垂直．
故答案为75°或120°或165°．
18．【解析】当正方形放在③的位置，即是中心对称图形．
故答案为：③．
三、解答题（本大题共6小题，共46分．解答时应写出文字说明、证明过程或演算步骤）
19．【解析】如图所示：
．
20．【解析】（1）甲图：平行四边形，
（2）乙图：等腰梯形，
（3）丙图：正方形．
21．【解析】（1）顶点A关于x轴对称的点A′的坐标（﹣4，﹣3），顶点B的坐标（3，0），
顶点C关于原点对称的点C′的坐标（2，﹣5）．
故答案为：﹣4，﹣3；3，0；2，﹣5；
（2）△ABC的面积为：12×5×5+2×5-12×2×2-12×3×7＝10．
故答案为：10．
22．【解析】（1）∵点A（2，3m）关于原点的对称点在第三象限，
∴点A在第一象限，
∴3m＞0，
解得m＞0；
（2）∵点B（3m﹣1，0.5m+2）到x轴的距离等于它到y轴距离的一半，
∴|0.5m+2|=12|3m﹣1|，
∴0.5m+2=12×（3m﹣1）或0.5m+2=-12×（3m﹣1），
解得m＝2.5或m=-34．
23．【解析】（1）下一步“马”可能到达的点的坐标：（0，0），（0，2），（1，3），（3，3），（4，2），（4，0）；
（2）连线可以看出得的图形为轴对称；
（3）将（2）中得到的图形的各顶点的坐标都乘以1.5，如图所示，与原图形比较，形状不变，图形变大了．
故答案为：（1）（0，0），（0，2），（1，3），（3，3），（4，2），（4，0）；（2）轴对称．
24．【解析】（1）由题意：-a+b+2=4-8a+2b+2=0，
解得a=1b=3，
∴函数解析式为y＝x3﹣3x+2．
故答案为y＝x3﹣3x+2．
（2）函数图象如图所示：
（3）①观察图象可知：函数图象关于（0，2）成中心对称．
故答案为（0，2）．
②观察图象可知：当﹣1＜x＜1时，y随着x的增大而减小．
③观察图象可知：若直线y＝c与该图象有3个交点，c的取值范围为0＜c＜4．