3.1 图形的平移同步练习(含解析)
文档属性
| 名称 | 3.1 图形的平移同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1003.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-18 22:51:16 | ||
图片预览




文档简介
3.1图形的平移
姓名:__________________ 班级:______________ 得分:_________________
注意事项:
本试卷满分100分,试题共24题,选择10道、填空8道、解答6道.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2020秋?道外区期末)观察下面图案,在下列四幅图案中,能通过图案平移得到的是( )
A. B.
C. D.
2.(2020秋?松江区期末)如图,△ABC沿射线BC方向平移到△DEF(点E在线段BC上),如果BC=8cm,EC=5cm,那么平移距离为( )
A.3cm B.5cm C.8cm D.13cm
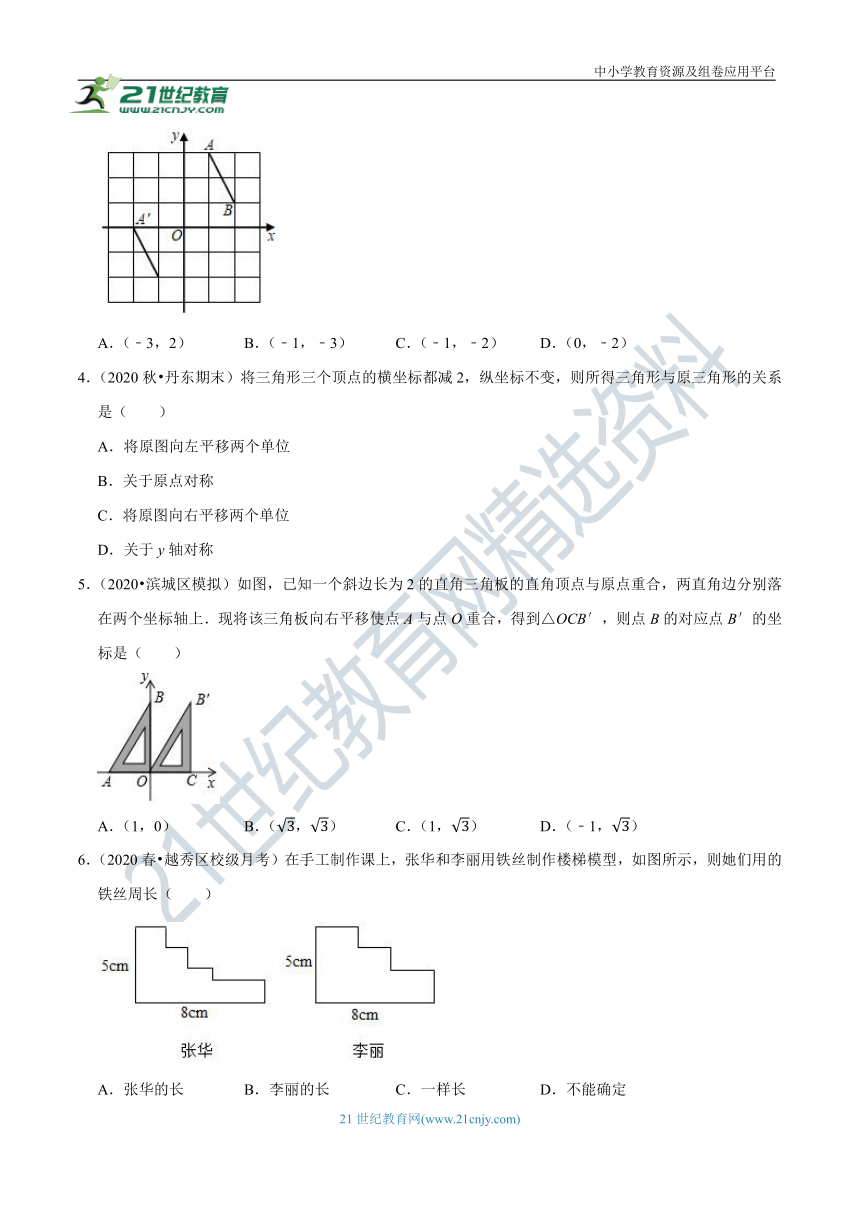
3.(2020秋?建邺区期末)如图,在平面直角坐标系中,线段AB的两个端点是A(1,3),B(2,1).将线段AB沿某一方向平移后,若点A的对应点A′的坐标为(﹣2,0),则点B的对应点B′的坐标为( )
A.(﹣3,2) B.(﹣1,﹣3) C.(﹣1,﹣2) D.(0,﹣2)
4.(2020秋?丹东期末)将三角形三个顶点的横坐标都减2,纵坐标不变,则所得三角形与原三角形的关系是( )
A.将原图向左平移两个单位
B.关于原点对称
C.将原图向右平移两个单位
D.关于y轴对称
5.(2020?滨城区模拟)如图,已知一个斜边长为2的直角三角板的直角顶点与原点重合,两直角边分别落在两个坐标轴上.现将该三角板向右平移使点A与点O重合,得到△OCB′,则点B的对应点B′的坐标是( )
A.(1,0) B.(3,3) C.(1,3) D.(﹣1,3)
6.(2020春?越秀区校级月考)在手工制作课上,张华和李丽用铁丝制作楼梯模型,如图所示,则她们用的铁丝周长( )
A.张华的长 B.李丽的长 C.一样长 D.不能确定
7.(2020春?越秀区校级期中)在平面直角坐标系中,已知线段MN的两个端点的坐标分别是M(﹣5,2)、N(1,﹣4),将线段MN向上移动3个单位,向左移动2个单位平移后,点M,N的对应坐标为( )
A.(﹣5,1),(0,﹣5) B.(﹣4,2),(1,﹣3)
C.(﹣7,5),(﹣1,﹣1) D.(﹣5,0),(1,﹣5)
8.(2020秋?西华县期中)如图,将一颗小星星放置在平面直角坐标系中第二象限内的甲位置,先将它绕原点O旋转180°到乙位置,再将它向上平移2个单位长到丙位置,则小星星顶点A在丙位置中的对应点A'的坐标为( )
A.(﹣3,1) B.(1,3) C.(3,1) D.(3,﹣1)
9.(2020春?仁寿县期末)如图,两个直角三角形重叠在一起,将△ABC沿AB方向平移2cm得到△DEF,CH=2cm,EF=4cm,下列结论:①BH∥EF;②AD=BE;③BD=CH;④∠C=∠BHD;⑤阴影部分的面积为6cm2.其中正确的是( )
A.①②③④⑤ B.②③④⑤ C.①②③⑤ D.①②④⑤
10.(2020春?娄星区期末)如图,在三角形ABC中,∠BAC=90°,AB=3cm,AC=4cm,把三角形ABC沿着直线BC向右平移2.5cm后得到三角形DEF,连接AE,AD,有以下结论:①AC∥DF; ②AD∥CF; ③CF=2.5cm;④DE⊥AC.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.(2020秋?香坊区期末)将点P(﹣3,1)向上平移2个单位长度得到点Q,则点Q的坐标为 .
12.(2020秋?武侯区校级期中)如图,将△ABC沿BC方向平移1cm得到△A'B'C',若△ABC的周长为8cm,则四边形ABC'A'的周长为 cm.
13.(2020?南关区校级四模)如图,在平面直角坐标系中,等边△OAB的边长为4,点A在第二象限内,点B在y轴正半轴,将△OAB沿射线AO平移,平移后点A'的横坐标为43,则点B'的横坐标为 .
14.(2020春?谢家集区期末)如图,在平面直角坐标系中,线段AB在x轴上,将线段AB向上平移2个单位.再向右平移1个单位,得到线段CD,连接AC,BD,在y轴上存在点P,使△PCD的面积为四边形ABDC面积的一半,则点P的坐标为 .
15.(2020春?汉阳区校级期中)如图,△ABC中,∠C=90°,AC=5cm,CB=12cm,AB=13cm,将△ABC沿直线CB向右平移3cm得到△DEF,DF交AB于点G,则点C到直线DE的距离为 cm.
16.(2020春?天宁区校级期中)如图,将长为5cm,宽为3cm的长方形ABCD先向右平移2cm,再向下平移1cm,得到长方形A'B'C'D',则阴影部分的面积为 cm2.
17.(2020春?历城区期中)如图,在△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移2个单位后,得到△A'B'C',连接A'C,则线段A'C的长为 .
18.(2020春?郫都区校级期中)在平面直角坐标系中,C(﹣1,5),D(﹣3,1),经过原点的直线m上有一点(3,2),平移线段CD,对应线段为EF(C对应E),若点E、F分别恰好在直线m和x轴上,则E点坐标为 .
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.(2020秋?道外区期末)已知,在平面直角坐标系中,三角形ABC三个顶点的坐标分别为A(5,6),B(﹣2,3),C(3,1).请在所给的平面直角坐标系中按要求完成以下问题:
(1)画出三角形ABC;
(2)将三角形ABC先向下平移6个单位长度,再向左平移3个单位长度后得到的三角形A1B1C1(点A1,B1,C1分别是点A,B,C移动后的对应点).
①请画出三角形A1B1C1;
②并判断线段AC与A1C1的位置与数量关系.
20.(2020秋?雨花区月考)如图,每个小方格都是边长为1个单位长度的正方形,△ABC的顶点都在格点上.
(1)求三角形ABC的面积;
(2)将△ABC平移后得到△DEF,若此时A点的对应点D的坐标为(1,3),请直接写出B点的对应点E和C点的对应点F的坐标,并在图中画出△DEF;
(3)在x轴上是否存在点P使得△DFP的面积与△ABC的面积相等,若存在,求出P点坐标,若不存在,请说明理由.
21.(2020秋?泰兴市期中)在平面直角坐标系中,点A的坐标为(0,4),线段MN的位置如图所示,其中点M的坐标为(﹣3,﹣1),点N的坐标为(3,﹣2).
(1)将线段MN平移得到线段AB,其中点M的对应点为A,点N的对应点为B.
①点M平移到点A的过程可以是:先向 平移 个单位长度,再向 平移 个单位长度;
②点B的坐标为 ;
(2)在(1)的条件下,若点C的坐标为(4,0),连接AC,BC,求△ABC的面积.
(3)在y轴上是否存在点P,使以A、B、P三点为顶点的三角形的面积为32,若存在,请直接写出点P的坐标;若不存在,请说明理由.
22.(2020春?惠来县期末)如图,AD∥BC,∠B=∠D=50°,点E、F在BC上,且满足∠CAD=∠CAE,AF平分∠BAE.
(1)∠CAF= °;
(2)若平行移动CD,那么∠ACB与∠AEB度数的比值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值;
(3)在平行移动CD的过程中,是否存在某种情况,使∠AFB=∠ACD?若存在,求出∠ACD度数;若不存在,说明理由.
23.(2019春?无棣县期中)如图,已知两条直线DM∥CN,线段AB的两个端点A、B分别在直线DM、CN上,∠C=∠BAD,点E在线段BC上,且DB平分∠ADE.
(1)求证:AB∥CD;
(2)若沿着NC方向平移线段AB,那么∠CBD与∠CED度数之间的关系是否随着AB位置的变化而变化?若变化,请找出变化规律;若不变化,请确定它们之间的数量关系.
24.(2019春?瑞安市期中)如图,已知C为两条相互平行的直线AB,ED之间一点,∠ABC和∠CDE的角平分线相交于F,∠FDC+∠ABC=180°.
(1)求证:AD∥BC.
(2)连结CF,当FC∥AB,且∠CFB=32∠DCF时,求∠BCD的度数.
(3)若∠DCF=∠CFB时,将线段BC沿射线AB方向平移,记平移后的线段为PQ(B,C分别对应P,Q,当∠PQD﹣∠QDC=20°时,请直接写出∠DQP的度数 .
答案
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.【解析】A、图案属于旋转所得到,故此选项不合题意;
B、图案形状与大小没有改变,符合平移性质,故此选项符合题意;
C、图案属于旋转所得到,故此选项不合题意;
D、图案属于旋转所得到,故此选项不合题意.
故选:B.
2.【解析】由题意平移的距离为BE=BC﹣EC=8﹣5=3(cm),
故选:A.
3.【解析】观察图象可知,点B的对应点B′的坐标为(﹣1,﹣2).
故选:C.
4.【解析】∵将三角形三个顶点的横坐标都减2,纵坐标不变,
∴所得三角形与原三角形的关系是:将原图向左平移两个单位.
故选:A.
5.【解析】在Rt△AOB中,∠AOB=90°,AB=2,∠ABO=30°,
∴AO=12AB=1,
∴OB=3OA=3,
∵△OB′C是由∠ABO平移得到,
∴OC=OA=1,B′C=OB=3,
∴B′(1,3).
故选:C.
6.【解析】因为经过平移两个图形可变为两个长和宽都相等长方形,所以她们用的铁丝周长一样长.
故选:C.
7.【解析】∵线段MN向上移动3个单位,向左移动2个单位平移,
∴平移后M(﹣5,2)、N(1,﹣4)对应坐标为(﹣5﹣2,2+3)、(1﹣2,﹣4+3),
即(﹣7,5),(﹣1,﹣1).
故选:C.
8.【解析】∵点A(﹣3,1)绕原点O旋转180°到乙位置,
∴A在乙位置时的坐标为(3,﹣1),
∵A在乙位置再将它向上平移2个单位长到丙位置,
∴丙位置中的对应点A′的坐标为(3,1).
故选:D.
9.【解析】因为将△ABC沿AB方向平移2cm得到△DEF,CH=2cm,EF=4cm,
所以:BC=BC,AB=DE,
∴BH∥EF,①正确;
∴AB﹣DB=DE﹣DB,
∴AD=BE,②正确;
③∵BC=EF=4cm,
∵CH=2cm,
∴BH=2cm,
∴BH是△DEF的中位线,
∴DB=BE=2cm,
∴BD=CH=2cm,正确;
∵BH∥EF,
∴∠BHD=∠F,
由平移性质可得:∠C=∠F,
∴∠C=∠BHD,④正确;
∵阴影部分的面积=△ABC的面积﹣△DBH的面积=6cm2.⑤正确;
故选:A.
10.【解析】∵△ABC沿着直线BC的方向平移2.5cm后得到△DEF,
∴AC∥DF,故①正确;
AD∥CF,故②正确;
CF=AD=2.5cm,故③正确;
AB∥DE,
又∵∠BAC=90°,
∴BA⊥AC,
∴DE⊥AC,故④正确;
故选:D.
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.【解析】将点P(﹣3,1)向上平移2个单位长度得到点Q,则点Q的坐标为(﹣3,1+2),即(﹣3,3),
故答案为:(﹣3,3).
12.【解析】∵△ABC沿BC方向平移1cm得到△A′B′C′,
∴AA′=CC′=1(cm),AC=A′C′,
∴四边形ABC′A′的周长=AB+(BC+CC′)+C′A′+AA′=AB+BC+AC+AC′+CC′,
∵△ABC的周长=8cm,
∴AB+BC+AC=8(cm),
∴四边形ABC′A′的周长=8+1+1=10(cm).
故答案为:10.
13.【解析】由题意得A(-23,2),B(0,4)
∵平移后点A'横坐标为43,
∴平移的规律为点A向右平移63,向下平移6个单位可得点A',
∴点B'坐标为(63,-2),
∴点B'横坐标为63,
故答案为63.
14.【解析】由平移可得,C(0,2),D(4,2),
∴CD=AB=4,CD∥AB,
∴四边形ABCD为平行四边形,
∴四边形ABCD面积=4×2=8,
又∵△PCD的面积为四边形ABCD面积的一半,
∴△PCD的面积为4,
即12×CD×CP=4,
∴CP=2,
∴当点P在CD下方时,P(0,0);当点P在CD上方时,P(0,4),
故答案为:(0,0)或(0,4).
15.【解析】如图,过点C作CH⊥DE于H.
在Rt△ACB中,∵∠ACB=90°,AC=5cm,BC=12cm,
∴AB=AC2+BC2=52+122=13(cm),
∵△DEF是由△ACB平移得到,
∴DE=AB=13(cm),EF=BC=12(cm),DF=AC=5(cm),
∵CF=3cm,
∴EC=CF+EF=15(cm),
∵sin∠E=CHCE=DFDE,
∴CH15=513,
∴CH=7513(cm).
故答案为7513.
16.【解析】由题意,阴影部分是矩形,长为5﹣2=3(cm),宽为3﹣1=2(cm),
∴阴影部分的面积=2×3=6(cm2),
故答案为6.
17.【解析】由题意,得BB′=2,
∴B′C=BC﹣BB′=4.
由平移性质,可知A′B′=AB=4,∠A′B′C=∠ABC=60°,
∴A′B′=B′C,且∠A′B′C=60°,
∴△A′B′C为等边三角形,
∴A'C=A'B'=4,
故答案为:4.
18.【解析】由题意点E的纵坐标为4,可得E(6,4),
∵点E向左平移2个单位,向下平移4个单位得到F,
∴F(4,0).
故答案为(6,4).
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.【解析】(1)如图所示,△ABC即为所求;
(2)如图所示,A1B1C1即为所求,AC与A1C1平行且相等.
20.【解析】(1)△ABC的面积为5×5-12×2×3-12×3×5-12×2×5=192;
(2)∵点A(﹣1,4)的对应点D的坐标为(1,3),
∴点B(﹣4,﹣1)的对应点E的坐标为(﹣4+2,﹣1﹣1),即E(﹣2,﹣2);
点C(1,1)的对应点F的坐标为(1+2,1﹣1),即F(3,0);
△DEF如图所示:
(3)存在,设点P的坐标为(x,0),
由题意得12×|x-3|×3=192,
解得x=283或-103,
所以点P为(283,0)或(-103,0).
21.【解析】(1)如图,点B即为所求作.
①点M平移到点A的过程可以是:先向右平移3个单位长度,再向上平移5个单位长度;
②点B的坐标为(6,3).
故答案为:右,3,上,5,(6,3).
(2)S△ABC=4×6-12×4×4-12×2×3-12×6×1=10.
(3)设P(0,m),由题意,12?|4﹣m|?6=32,
解得m=3.5和4.5,
∴P(0,3.5),或(0,4.5).
22.【解析】(1)∵AD∥BC,
∴∠B+∠BAD=180°,
∵∠B=50°,
∴∠BAD=130°,
∵AF平分∠BAE,
∴∠BAF=∠EAF,
∵∠CAD=∠CAE,
∴∠CAF=12∠BAE+12∠DAE=12∠BAD=65°,
故答案为65.
(2)结论:∠ACB与∠AEB度数的比值不变.
理由:∵AD∥BC,
∴∠CAD=∠ACE,
∵∠CAD=∠CAE,
∴∠ACE=∠CAE,
∵∠AEB=∠ACE+∠CAE=2∠ACB,
∴∠ACB:∠AEB=1:2.
(3)设∠ACD=x,∠CAD=y.
则有x+y=130°,
∵∠AFB=∠ACD=∠ACB+∠CAF,
∴x=65°+y,
解得x=97.5°,
∴∠ACD=97.5°.
23.【解析】(1)∵DM∥CN,
∴∠BAD=∠NBA,
∵∠C=∠BAD,
∴∠C=∠NBA,
∴AB∥CD.
(2)结论:没有变化,∠CDB=12∠CED.
理由:∵DB平分∠ADE,
∴∠ADB=∠EDB,
∵DM∥CN,
∴∠ADB=∠CBD,
∴∠CBD=∠EDB,
∵DM∥CN,
∴∠CED=∠EDA,
∵∠EDA=2∠EDB,
∴∠CDB=12∠CED.
24.【解析】(1)证明:∵AB∥DE,
∴∠EDF=∠DAB,
∵DF平分∠EDC,
∴∠EDF=∠ADC,
∴∠ADC=∠DAB,
∵∠FDC+∠ABC=180°,
∴∠DAB+∠ABC=180°,
∴AD∥BC;
(2)∵∠CFB=32∠DCF,
∴设∠DCF=α,则∠CFB=1.5α,
∵CF∥AB,
∴∠ABF=∠CFB=1.5α,
∵BE平分∠ABC,
∴∠ABC=2∠ABF=3α,
∵AD∥BC,
∴∠ADC+∠BCD=180°,
∵∠FDC+∠ABC=180°,
∴∠BCD=∠ABC=3α,
∴∠BCF=2α,
∵CF∥AB,
∴∠ABC+∠BCF=180°,
∴3α+2α=180°,
∴α=36°,
∴∠BCD=3×36°=108°;
(3)如图,∵∠DCF=∠CFB,
∴BF∥CD,
∵AD∥BC,
∴四边形BCDF是平行四边形,
∴∠CDF=∠CBF,
∵AD,BE分别平分∠ABC,∠CDE,
∴∠ABC=2∠CBF,∠CDE=2∠CDF,
∴∠ABC=2∠CDF,
∵∠FDC+∠ABC=180°,
∴∠ABC=120°,∠CDF=60°,
∴∠DCB=120°,
∴∠ABC=120°,
∴∠DAB=60°,
∵线段BC沿直线AB方向平移得到线段PQ,
∴BC∥PQ,
∴∠APQ=120°,
∵∠PQD﹣∠QDC=20°,
∴∠QDC=∠PQD﹣20°,
∴∠FDC+∠CDQ+∠PQD+∠APQ+∠DAB=60°+∠PQD﹣20°+∠PQD+120°+60°=360°,
∴∠PQD=70°.
故答案为:70°.
姓名:__________________ 班级:______________ 得分:_________________
注意事项:
本试卷满分100分,试题共24题,选择10道、填空8道、解答6道.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2020秋?道外区期末)观察下面图案,在下列四幅图案中,能通过图案平移得到的是( )
A. B.
C. D.
2.(2020秋?松江区期末)如图,△ABC沿射线BC方向平移到△DEF(点E在线段BC上),如果BC=8cm,EC=5cm,那么平移距离为( )
A.3cm B.5cm C.8cm D.13cm
3.(2020秋?建邺区期末)如图,在平面直角坐标系中,线段AB的两个端点是A(1,3),B(2,1).将线段AB沿某一方向平移后,若点A的对应点A′的坐标为(﹣2,0),则点B的对应点B′的坐标为( )
A.(﹣3,2) B.(﹣1,﹣3) C.(﹣1,﹣2) D.(0,﹣2)
4.(2020秋?丹东期末)将三角形三个顶点的横坐标都减2,纵坐标不变,则所得三角形与原三角形的关系是( )
A.将原图向左平移两个单位
B.关于原点对称
C.将原图向右平移两个单位
D.关于y轴对称
5.(2020?滨城区模拟)如图,已知一个斜边长为2的直角三角板的直角顶点与原点重合,两直角边分别落在两个坐标轴上.现将该三角板向右平移使点A与点O重合,得到△OCB′,则点B的对应点B′的坐标是( )
A.(1,0) B.(3,3) C.(1,3) D.(﹣1,3)
6.(2020春?越秀区校级月考)在手工制作课上,张华和李丽用铁丝制作楼梯模型,如图所示,则她们用的铁丝周长( )
A.张华的长 B.李丽的长 C.一样长 D.不能确定
7.(2020春?越秀区校级期中)在平面直角坐标系中,已知线段MN的两个端点的坐标分别是M(﹣5,2)、N(1,﹣4),将线段MN向上移动3个单位,向左移动2个单位平移后,点M,N的对应坐标为( )
A.(﹣5,1),(0,﹣5) B.(﹣4,2),(1,﹣3)
C.(﹣7,5),(﹣1,﹣1) D.(﹣5,0),(1,﹣5)
8.(2020秋?西华县期中)如图,将一颗小星星放置在平面直角坐标系中第二象限内的甲位置,先将它绕原点O旋转180°到乙位置,再将它向上平移2个单位长到丙位置,则小星星顶点A在丙位置中的对应点A'的坐标为( )
A.(﹣3,1) B.(1,3) C.(3,1) D.(3,﹣1)
9.(2020春?仁寿县期末)如图,两个直角三角形重叠在一起,将△ABC沿AB方向平移2cm得到△DEF,CH=2cm,EF=4cm,下列结论:①BH∥EF;②AD=BE;③BD=CH;④∠C=∠BHD;⑤阴影部分的面积为6cm2.其中正确的是( )
A.①②③④⑤ B.②③④⑤ C.①②③⑤ D.①②④⑤
10.(2020春?娄星区期末)如图,在三角形ABC中,∠BAC=90°,AB=3cm,AC=4cm,把三角形ABC沿着直线BC向右平移2.5cm后得到三角形DEF,连接AE,AD,有以下结论:①AC∥DF; ②AD∥CF; ③CF=2.5cm;④DE⊥AC.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.(2020秋?香坊区期末)将点P(﹣3,1)向上平移2个单位长度得到点Q,则点Q的坐标为 .
12.(2020秋?武侯区校级期中)如图,将△ABC沿BC方向平移1cm得到△A'B'C',若△ABC的周长为8cm,则四边形ABC'A'的周长为 cm.
13.(2020?南关区校级四模)如图,在平面直角坐标系中,等边△OAB的边长为4,点A在第二象限内,点B在y轴正半轴,将△OAB沿射线AO平移,平移后点A'的横坐标为43,则点B'的横坐标为 .
14.(2020春?谢家集区期末)如图,在平面直角坐标系中,线段AB在x轴上,将线段AB向上平移2个单位.再向右平移1个单位,得到线段CD,连接AC,BD,在y轴上存在点P,使△PCD的面积为四边形ABDC面积的一半,则点P的坐标为 .
15.(2020春?汉阳区校级期中)如图,△ABC中,∠C=90°,AC=5cm,CB=12cm,AB=13cm,将△ABC沿直线CB向右平移3cm得到△DEF,DF交AB于点G,则点C到直线DE的距离为 cm.
16.(2020春?天宁区校级期中)如图,将长为5cm,宽为3cm的长方形ABCD先向右平移2cm,再向下平移1cm,得到长方形A'B'C'D',则阴影部分的面积为 cm2.
17.(2020春?历城区期中)如图,在△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移2个单位后,得到△A'B'C',连接A'C,则线段A'C的长为 .
18.(2020春?郫都区校级期中)在平面直角坐标系中,C(﹣1,5),D(﹣3,1),经过原点的直线m上有一点(3,2),平移线段CD,对应线段为EF(C对应E),若点E、F分别恰好在直线m和x轴上,则E点坐标为 .
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.(2020秋?道外区期末)已知,在平面直角坐标系中,三角形ABC三个顶点的坐标分别为A(5,6),B(﹣2,3),C(3,1).请在所给的平面直角坐标系中按要求完成以下问题:
(1)画出三角形ABC;
(2)将三角形ABC先向下平移6个单位长度,再向左平移3个单位长度后得到的三角形A1B1C1(点A1,B1,C1分别是点A,B,C移动后的对应点).
①请画出三角形A1B1C1;
②并判断线段AC与A1C1的位置与数量关系.
20.(2020秋?雨花区月考)如图,每个小方格都是边长为1个单位长度的正方形,△ABC的顶点都在格点上.
(1)求三角形ABC的面积;
(2)将△ABC平移后得到△DEF,若此时A点的对应点D的坐标为(1,3),请直接写出B点的对应点E和C点的对应点F的坐标,并在图中画出△DEF;
(3)在x轴上是否存在点P使得△DFP的面积与△ABC的面积相等,若存在,求出P点坐标,若不存在,请说明理由.
21.(2020秋?泰兴市期中)在平面直角坐标系中,点A的坐标为(0,4),线段MN的位置如图所示,其中点M的坐标为(﹣3,﹣1),点N的坐标为(3,﹣2).
(1)将线段MN平移得到线段AB,其中点M的对应点为A,点N的对应点为B.
①点M平移到点A的过程可以是:先向 平移 个单位长度,再向 平移 个单位长度;
②点B的坐标为 ;
(2)在(1)的条件下,若点C的坐标为(4,0),连接AC,BC,求△ABC的面积.
(3)在y轴上是否存在点P,使以A、B、P三点为顶点的三角形的面积为32,若存在,请直接写出点P的坐标;若不存在,请说明理由.
22.(2020春?惠来县期末)如图,AD∥BC,∠B=∠D=50°,点E、F在BC上,且满足∠CAD=∠CAE,AF平分∠BAE.
(1)∠CAF= °;
(2)若平行移动CD,那么∠ACB与∠AEB度数的比值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值;
(3)在平行移动CD的过程中,是否存在某种情况,使∠AFB=∠ACD?若存在,求出∠ACD度数;若不存在,说明理由.
23.(2019春?无棣县期中)如图,已知两条直线DM∥CN,线段AB的两个端点A、B分别在直线DM、CN上,∠C=∠BAD,点E在线段BC上,且DB平分∠ADE.
(1)求证:AB∥CD;
(2)若沿着NC方向平移线段AB,那么∠CBD与∠CED度数之间的关系是否随着AB位置的变化而变化?若变化,请找出变化规律;若不变化,请确定它们之间的数量关系.
24.(2019春?瑞安市期中)如图,已知C为两条相互平行的直线AB,ED之间一点,∠ABC和∠CDE的角平分线相交于F,∠FDC+∠ABC=180°.
(1)求证:AD∥BC.
(2)连结CF,当FC∥AB,且∠CFB=32∠DCF时,求∠BCD的度数.
(3)若∠DCF=∠CFB时,将线段BC沿射线AB方向平移,记平移后的线段为PQ(B,C分别对应P,Q,当∠PQD﹣∠QDC=20°时,请直接写出∠DQP的度数 .
答案
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.【解析】A、图案属于旋转所得到,故此选项不合题意;
B、图案形状与大小没有改变,符合平移性质,故此选项符合题意;
C、图案属于旋转所得到,故此选项不合题意;
D、图案属于旋转所得到,故此选项不合题意.
故选:B.
2.【解析】由题意平移的距离为BE=BC﹣EC=8﹣5=3(cm),
故选:A.
3.【解析】观察图象可知,点B的对应点B′的坐标为(﹣1,﹣2).
故选:C.
4.【解析】∵将三角形三个顶点的横坐标都减2,纵坐标不变,
∴所得三角形与原三角形的关系是:将原图向左平移两个单位.
故选:A.
5.【解析】在Rt△AOB中,∠AOB=90°,AB=2,∠ABO=30°,
∴AO=12AB=1,
∴OB=3OA=3,
∵△OB′C是由∠ABO平移得到,
∴OC=OA=1,B′C=OB=3,
∴B′(1,3).
故选:C.
6.【解析】因为经过平移两个图形可变为两个长和宽都相等长方形,所以她们用的铁丝周长一样长.
故选:C.
7.【解析】∵线段MN向上移动3个单位,向左移动2个单位平移,
∴平移后M(﹣5,2)、N(1,﹣4)对应坐标为(﹣5﹣2,2+3)、(1﹣2,﹣4+3),
即(﹣7,5),(﹣1,﹣1).
故选:C.
8.【解析】∵点A(﹣3,1)绕原点O旋转180°到乙位置,
∴A在乙位置时的坐标为(3,﹣1),
∵A在乙位置再将它向上平移2个单位长到丙位置,
∴丙位置中的对应点A′的坐标为(3,1).
故选:D.
9.【解析】因为将△ABC沿AB方向平移2cm得到△DEF,CH=2cm,EF=4cm,
所以:BC=BC,AB=DE,
∴BH∥EF,①正确;
∴AB﹣DB=DE﹣DB,
∴AD=BE,②正确;
③∵BC=EF=4cm,
∵CH=2cm,
∴BH=2cm,
∴BH是△DEF的中位线,
∴DB=BE=2cm,
∴BD=CH=2cm,正确;
∵BH∥EF,
∴∠BHD=∠F,
由平移性质可得:∠C=∠F,
∴∠C=∠BHD,④正确;
∵阴影部分的面积=△ABC的面积﹣△DBH的面积=6cm2.⑤正确;
故选:A.
10.【解析】∵△ABC沿着直线BC的方向平移2.5cm后得到△DEF,
∴AC∥DF,故①正确;
AD∥CF,故②正确;
CF=AD=2.5cm,故③正确;
AB∥DE,
又∵∠BAC=90°,
∴BA⊥AC,
∴DE⊥AC,故④正确;
故选:D.
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.【解析】将点P(﹣3,1)向上平移2个单位长度得到点Q,则点Q的坐标为(﹣3,1+2),即(﹣3,3),
故答案为:(﹣3,3).
12.【解析】∵△ABC沿BC方向平移1cm得到△A′B′C′,
∴AA′=CC′=1(cm),AC=A′C′,
∴四边形ABC′A′的周长=AB+(BC+CC′)+C′A′+AA′=AB+BC+AC+AC′+CC′,
∵△ABC的周长=8cm,
∴AB+BC+AC=8(cm),
∴四边形ABC′A′的周长=8+1+1=10(cm).
故答案为:10.
13.【解析】由题意得A(-23,2),B(0,4)
∵平移后点A'横坐标为43,
∴平移的规律为点A向右平移63,向下平移6个单位可得点A',
∴点B'坐标为(63,-2),
∴点B'横坐标为63,
故答案为63.
14.【解析】由平移可得,C(0,2),D(4,2),
∴CD=AB=4,CD∥AB,
∴四边形ABCD为平行四边形,
∴四边形ABCD面积=4×2=8,
又∵△PCD的面积为四边形ABCD面积的一半,
∴△PCD的面积为4,
即12×CD×CP=4,
∴CP=2,
∴当点P在CD下方时,P(0,0);当点P在CD上方时,P(0,4),
故答案为:(0,0)或(0,4).
15.【解析】如图,过点C作CH⊥DE于H.
在Rt△ACB中,∵∠ACB=90°,AC=5cm,BC=12cm,
∴AB=AC2+BC2=52+122=13(cm),
∵△DEF是由△ACB平移得到,
∴DE=AB=13(cm),EF=BC=12(cm),DF=AC=5(cm),
∵CF=3cm,
∴EC=CF+EF=15(cm),
∵sin∠E=CHCE=DFDE,
∴CH15=513,
∴CH=7513(cm).
故答案为7513.
16.【解析】由题意,阴影部分是矩形,长为5﹣2=3(cm),宽为3﹣1=2(cm),
∴阴影部分的面积=2×3=6(cm2),
故答案为6.
17.【解析】由题意,得BB′=2,
∴B′C=BC﹣BB′=4.
由平移性质,可知A′B′=AB=4,∠A′B′C=∠ABC=60°,
∴A′B′=B′C,且∠A′B′C=60°,
∴△A′B′C为等边三角形,
∴A'C=A'B'=4,
故答案为:4.
18.【解析】由题意点E的纵坐标为4,可得E(6,4),
∵点E向左平移2个单位,向下平移4个单位得到F,
∴F(4,0).
故答案为(6,4).
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.【解析】(1)如图所示,△ABC即为所求;
(2)如图所示,A1B1C1即为所求,AC与A1C1平行且相等.
20.【解析】(1)△ABC的面积为5×5-12×2×3-12×3×5-12×2×5=192;
(2)∵点A(﹣1,4)的对应点D的坐标为(1,3),
∴点B(﹣4,﹣1)的对应点E的坐标为(﹣4+2,﹣1﹣1),即E(﹣2,﹣2);
点C(1,1)的对应点F的坐标为(1+2,1﹣1),即F(3,0);
△DEF如图所示:
(3)存在,设点P的坐标为(x,0),
由题意得12×|x-3|×3=192,
解得x=283或-103,
所以点P为(283,0)或(-103,0).
21.【解析】(1)如图,点B即为所求作.
①点M平移到点A的过程可以是:先向右平移3个单位长度,再向上平移5个单位长度;
②点B的坐标为(6,3).
故答案为:右,3,上,5,(6,3).
(2)S△ABC=4×6-12×4×4-12×2×3-12×6×1=10.
(3)设P(0,m),由题意,12?|4﹣m|?6=32,
解得m=3.5和4.5,
∴P(0,3.5),或(0,4.5).
22.【解析】(1)∵AD∥BC,
∴∠B+∠BAD=180°,
∵∠B=50°,
∴∠BAD=130°,
∵AF平分∠BAE,
∴∠BAF=∠EAF,
∵∠CAD=∠CAE,
∴∠CAF=12∠BAE+12∠DAE=12∠BAD=65°,
故答案为65.
(2)结论:∠ACB与∠AEB度数的比值不变.
理由:∵AD∥BC,
∴∠CAD=∠ACE,
∵∠CAD=∠CAE,
∴∠ACE=∠CAE,
∵∠AEB=∠ACE+∠CAE=2∠ACB,
∴∠ACB:∠AEB=1:2.
(3)设∠ACD=x,∠CAD=y.
则有x+y=130°,
∵∠AFB=∠ACD=∠ACB+∠CAF,
∴x=65°+y,
解得x=97.5°,
∴∠ACD=97.5°.
23.【解析】(1)∵DM∥CN,
∴∠BAD=∠NBA,
∵∠C=∠BAD,
∴∠C=∠NBA,
∴AB∥CD.
(2)结论:没有变化,∠CDB=12∠CED.
理由:∵DB平分∠ADE,
∴∠ADB=∠EDB,
∵DM∥CN,
∴∠ADB=∠CBD,
∴∠CBD=∠EDB,
∵DM∥CN,
∴∠CED=∠EDA,
∵∠EDA=2∠EDB,
∴∠CDB=12∠CED.
24.【解析】(1)证明:∵AB∥DE,
∴∠EDF=∠DAB,
∵DF平分∠EDC,
∴∠EDF=∠ADC,
∴∠ADC=∠DAB,
∵∠FDC+∠ABC=180°,
∴∠DAB+∠ABC=180°,
∴AD∥BC;
(2)∵∠CFB=32∠DCF,
∴设∠DCF=α,则∠CFB=1.5α,
∵CF∥AB,
∴∠ABF=∠CFB=1.5α,
∵BE平分∠ABC,
∴∠ABC=2∠ABF=3α,
∵AD∥BC,
∴∠ADC+∠BCD=180°,
∵∠FDC+∠ABC=180°,
∴∠BCD=∠ABC=3α,
∴∠BCF=2α,
∵CF∥AB,
∴∠ABC+∠BCF=180°,
∴3α+2α=180°,
∴α=36°,
∴∠BCD=3×36°=108°;
(3)如图,∵∠DCF=∠CFB,
∴BF∥CD,
∵AD∥BC,
∴四边形BCDF是平行四边形,
∴∠CDF=∠CBF,
∵AD,BE分别平分∠ABC,∠CDE,
∴∠ABC=2∠CBF,∠CDE=2∠CDF,
∴∠ABC=2∠CDF,
∵∠FDC+∠ABC=180°,
∴∠ABC=120°,∠CDF=60°,
∴∠DCB=120°,
∴∠ABC=120°,
∴∠DAB=60°,
∵线段BC沿直线AB方向平移得到线段PQ,
∴BC∥PQ,
∴∠APQ=120°,
∵∠PQD﹣∠QDC=20°,
∴∠QDC=∠PQD﹣20°,
∴∠FDC+∠CDQ+∠PQD+∠APQ+∠DAB=60°+∠PQD﹣20°+∠PQD+120°+60°=360°,
∴∠PQD=70°.
故答案为:70°.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
