2020--2021学年人教版八年级数学下册第十七章勾股定理 小结与复习(26张)
文档属性
| 名称 | 2020--2021学年人教版八年级数学下册第十七章勾股定理 小结与复习(26张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 419.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-19 00:00:00 | ||
图片预览







文档简介
勾股定理
勾股定理小结与复习习题练习
勾
股
定
理
发现
应用
勾股
定理
证明
赵爽弦图
毕达哥拉斯
美国总统
在数轴上表示某些无理数
生活应用
旗杆、梯子、河水深度等问题
勾股定理的逆定理
内容
应用
已知三角形的三边长,判断是否是直角三角形
综合应用
折纸中的勾股定理
路程最短问题
拼图加面积法
猜想
直角三角形,已知两边,求第三边
勾股数
分类思想
特殊例子
用割、补法求图形面积
精彩回放
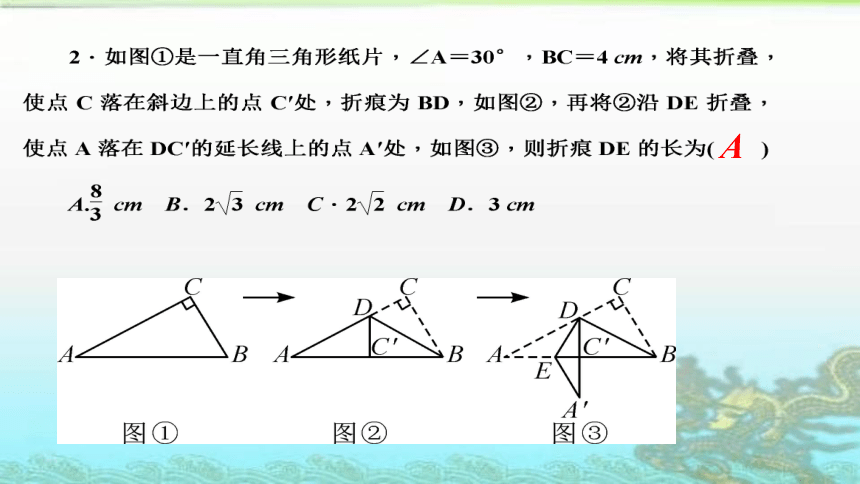
C
一 选择题
A
3.在Rt△ABC中,∠C=90°.
(1)如果a=3,b=4, 则c= (2)如果a=12,c=20, 则b=
(3)如果c=13,b=12,则a= (4)已知b=3,∠A=30°,求a,c.
答案:(4)a= ,c= .
5
16
5
基础训练检测
二 填空题
4、在Rt△ABC中,已知a=1,b=3,∠B=90°,则第三边c的长为 .
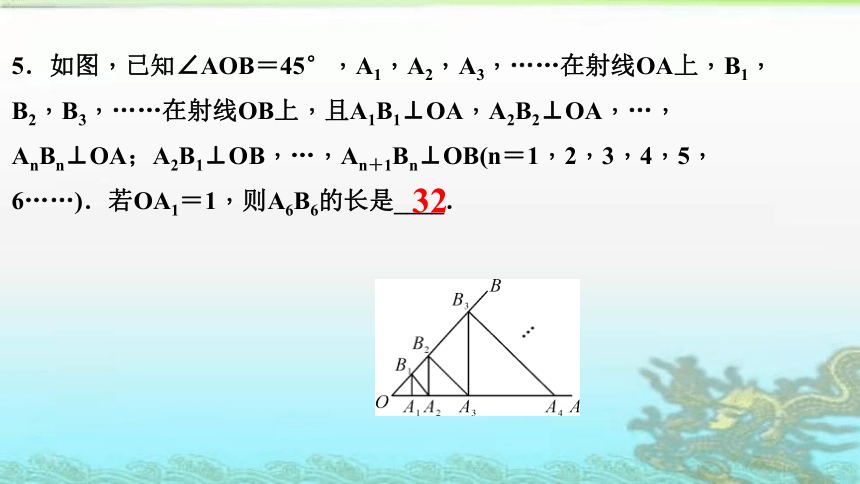
5.如图,已知∠AOB=45°,A1,A2,A3,……在射线OA上,B1,B2,B3,……在射线OB上,且A1B1⊥OA,A2B2⊥OA,…,AnBn⊥OA;A2B1⊥OB,…,An+1Bn⊥OB(n=1,2,3,4,5,6……).若OA1=1,则A6B6的长是____.
32
或
7、分别以下列四组数为一个三角形的边长:
①3,4,5; ②5,12,13; ③8,15,17; ④4,5,6.
其中能构成
直角三角形的有 .
①②③
6、在Rt△ABC中,已知a=1,b=3,则第三边c的长为 .
9.如图,已知在△ABC 中,∠B =90°,若BC=4 , AB=x ,AC=8-x,则AB= ,AC= .
10.在Rt△ABC 中,∠B=90°,b=34,a:c=8:15,则
a= , c= .
3
5
16
30
注意:要树立方程思想
11.如图,透明的圆柱形容器(容器厚度忽略不计)的高为12 cm,底面周长为10 cm,在容器内壁离容器底部3 cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3 cm的点A处,则蚂蚁吃到饭粒需爬行的最短路径是____cm.
13
12.如图,在一个长为2 m,宽为1 m的长方形草地上,放着一根长方体的木块,它的棱和场地宽AD平行且棱长大于AD,木块从正面看是边长为0.2 m的正方形,一只蚂蚁从点A处到达C处需要走的最短路程是________m.(精确到0.01 m)
2.60
13.图①所示的正方体木块棱长为6 cm,沿其相邻三个面的对角线(图中虚线)剪掉一角,得到如图②的几何体,一只蚂蚁沿着图②的几何体表面从顶点A爬行到顶点B的最短距离为____________cm.
14 已知Rt△ABC中,∠C=90°,若a+b=14,c=10,则Rt△ABC的面积是_______
24
10 cm
15 一个直角三角形的周长为24cm,面积为24cm?,则斜边长为_____
16.如图,在Rt△ABC中,∠ABC=90°,AB=3,AC=5,点E在BC上,将△ABC沿AE折叠,使点B落在AC边上的点B′处,求BE的长.
三 解答
17 已知:如图,AD是△ABC的高,AB=10,AD=8,BC=12 .
求证: △ABC是等腰三角形.
证明:∵AD是△ABC的高,
∴∠ADB=∠ADC=90°.
∵在Rt△ADB中,AB=10,AD=8,
∴BD=6 .
∵BC=12, ∴DC=6.
∵在Rt△ADC中,AD=8,
∴AC=10,
∴AB=AC.即△ABC是等腰三角形.
18 已知如图,将长方形的一边BC沿CE折叠,
使得点B落在AD边的点F处,已知AB=8,
BC=10, 求BE的长.
解:设BE=x,折叠,∴△BCE ≌△FCE,
∴BC=FC=10. 令BE=FE=x,长方形ABCD,
∴ AB=DC=8 ,AD=BC=10,∠D=90°,
∴DF=6, AF=4,∠A=90°, AE=8-x ,
∴ ,
解得 x = 5 .∴BE的长为5.
19 已知:如图,在△ABC中,∠B=45°,∠C=60°,AB=2.求(1)BC 的长;(2)S△ABC?.
解:过点A作AD⊥BC于D,∴∠ADB=∠ADC=90°.
在△ABD中,∠ADB=90°,
∠B=45°,AB=2,∴AD=BD= .∵在△ABD中,∠ADC=90°,∠C=60°,AD= ,
∴CD= ,∴BC= ,S△ABC?=
20.如图,长方形ABCD的边AD沿折痕AE折叠,使点D落在BC上的F处,已知AB=6,△ABF的面积是24,求EF的长.
解:当高AD在△ABC内部时,如图①.
在Rt△ABD中,由勾股定理,
得BD2=AB2-AD2=202-122=162,
∴BD=16.
在Rt△ACD中,由勾股定理,
得CD2=AC2-AD2=152-122=81,
∴CD=9.∴BC=BD+CD=25,
∴△ABC的周长为25+20+15=60.
21 在△ABC中,AB=20,AC=15,AD为BC边上的高,且AD=12,求△ABC的周长.
当高AD在△ABC外部时,如图②.
同理可得 BD=16,CD=9.
∴BC=BD-CD=7,
∴△ABC的周长为7+20+15=42.
综上所述,△ABC的周长为42或60.
C
22 如图,一条河同一侧的两村庄A、B,其中A、B到河岸最短距离分别为AC=1km,BD=2km,CD=4km,现欲在河岸上M处建一个水泵站向A、B两村送水,当M在河岸上何处时,到A、B两村铺设水管总长度最短,并求出最短距离。
A
M
B
A′
D
E
1
2
4
1
1
4
5
23、如图,将一根25cm长的细木棍放入长,宽高分别为8cm、6cm、和 cm的长方体无盖盒子中,求细木棍露在外面的最短长度是多少?
A
B
C
D
E
8
6
25
10
20
5
24、如图,四边形ABCD中,∠B=900,AB=20,BC=15,CD=7,AD=24,求证∠A+ ∠C=1800。
25
转化思想
25、如图所示是一块地,已知AD=8米,CD=6米,∠D=900,AB=26米,BC=24米,求这块地的面积
26、 格点三角形
∠ BCD是直角吗?
谢谢观看
勾股定理小结与复习习题练习
勾
股
定
理
发现
应用
勾股
定理
证明
赵爽弦图
毕达哥拉斯
美国总统
在数轴上表示某些无理数
生活应用
旗杆、梯子、河水深度等问题
勾股定理的逆定理
内容
应用
已知三角形的三边长,判断是否是直角三角形
综合应用
折纸中的勾股定理
路程最短问题
拼图加面积法
猜想
直角三角形,已知两边,求第三边
勾股数
分类思想
特殊例子
用割、补法求图形面积
精彩回放
C
一 选择题
A
3.在Rt△ABC中,∠C=90°.
(1)如果a=3,b=4, 则c= (2)如果a=12,c=20, 则b=
(3)如果c=13,b=12,则a= (4)已知b=3,∠A=30°,求a,c.
答案:(4)a= ,c= .
5
16
5
基础训练检测
二 填空题
4、在Rt△ABC中,已知a=1,b=3,∠B=90°,则第三边c的长为 .
5.如图,已知∠AOB=45°,A1,A2,A3,……在射线OA上,B1,B2,B3,……在射线OB上,且A1B1⊥OA,A2B2⊥OA,…,AnBn⊥OA;A2B1⊥OB,…,An+1Bn⊥OB(n=1,2,3,4,5,6……).若OA1=1,则A6B6的长是____.
32
或
7、分别以下列四组数为一个三角形的边长:
①3,4,5; ②5,12,13; ③8,15,17; ④4,5,6.
其中能构成
直角三角形的有 .
①②③
6、在Rt△ABC中,已知a=1,b=3,则第三边c的长为 .
9.如图,已知在△ABC 中,∠B =90°,若BC=4 , AB=x ,AC=8-x,则AB= ,AC= .
10.在Rt△ABC 中,∠B=90°,b=34,a:c=8:15,则
a= , c= .
3
5
16
30
注意:要树立方程思想
11.如图,透明的圆柱形容器(容器厚度忽略不计)的高为12 cm,底面周长为10 cm,在容器内壁离容器底部3 cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3 cm的点A处,则蚂蚁吃到饭粒需爬行的最短路径是____cm.
13
12.如图,在一个长为2 m,宽为1 m的长方形草地上,放着一根长方体的木块,它的棱和场地宽AD平行且棱长大于AD,木块从正面看是边长为0.2 m的正方形,一只蚂蚁从点A处到达C处需要走的最短路程是________m.(精确到0.01 m)
2.60
13.图①所示的正方体木块棱长为6 cm,沿其相邻三个面的对角线(图中虚线)剪掉一角,得到如图②的几何体,一只蚂蚁沿着图②的几何体表面从顶点A爬行到顶点B的最短距离为____________cm.
14 已知Rt△ABC中,∠C=90°,若a+b=14,c=10,则Rt△ABC的面积是_______
24
10 cm
15 一个直角三角形的周长为24cm,面积为24cm?,则斜边长为_____
16.如图,在Rt△ABC中,∠ABC=90°,AB=3,AC=5,点E在BC上,将△ABC沿AE折叠,使点B落在AC边上的点B′处,求BE的长.
三 解答
17 已知:如图,AD是△ABC的高,AB=10,AD=8,BC=12 .
求证: △ABC是等腰三角形.
证明:∵AD是△ABC的高,
∴∠ADB=∠ADC=90°.
∵在Rt△ADB中,AB=10,AD=8,
∴BD=6 .
∵BC=12, ∴DC=6.
∵在Rt△ADC中,AD=8,
∴AC=10,
∴AB=AC.即△ABC是等腰三角形.
18 已知如图,将长方形的一边BC沿CE折叠,
使得点B落在AD边的点F处,已知AB=8,
BC=10, 求BE的长.
解:设BE=x,折叠,∴△BCE ≌△FCE,
∴BC=FC=10. 令BE=FE=x,长方形ABCD,
∴ AB=DC=8 ,AD=BC=10,∠D=90°,
∴DF=6, AF=4,∠A=90°, AE=8-x ,
∴ ,
解得 x = 5 .∴BE的长为5.
19 已知:如图,在△ABC中,∠B=45°,∠C=60°,AB=2.求(1)BC 的长;(2)S△ABC?.
解:过点A作AD⊥BC于D,∴∠ADB=∠ADC=90°.
在△ABD中,∠ADB=90°,
∠B=45°,AB=2,∴AD=BD= .∵在△ABD中,∠ADC=90°,∠C=60°,AD= ,
∴CD= ,∴BC= ,S△ABC?=
20.如图,长方形ABCD的边AD沿折痕AE折叠,使点D落在BC上的F处,已知AB=6,△ABF的面积是24,求EF的长.
解:当高AD在△ABC内部时,如图①.
在Rt△ABD中,由勾股定理,
得BD2=AB2-AD2=202-122=162,
∴BD=16.
在Rt△ACD中,由勾股定理,
得CD2=AC2-AD2=152-122=81,
∴CD=9.∴BC=BD+CD=25,
∴△ABC的周长为25+20+15=60.
21 在△ABC中,AB=20,AC=15,AD为BC边上的高,且AD=12,求△ABC的周长.
当高AD在△ABC外部时,如图②.
同理可得 BD=16,CD=9.
∴BC=BD-CD=7,
∴△ABC的周长为7+20+15=42.
综上所述,△ABC的周长为42或60.
C
22 如图,一条河同一侧的两村庄A、B,其中A、B到河岸最短距离分别为AC=1km,BD=2km,CD=4km,现欲在河岸上M处建一个水泵站向A、B两村送水,当M在河岸上何处时,到A、B两村铺设水管总长度最短,并求出最短距离。
A
M
B
A′
D
E
1
2
4
1
1
4
5
23、如图,将一根25cm长的细木棍放入长,宽高分别为8cm、6cm、和 cm的长方体无盖盒子中,求细木棍露在外面的最短长度是多少?
A
B
C
D
E
8
6
25
10
20
5
24、如图,四边形ABCD中,∠B=900,AB=20,BC=15,CD=7,AD=24,求证∠A+ ∠C=1800。
25
转化思想
25、如图所示是一块地,已知AD=8米,CD=6米,∠D=900,AB=26米,BC=24米,求这块地的面积
26、 格点三角形
∠ BCD是直角吗?
谢谢观看
