全等三角形复习学案(田畔中学黎汝华)
文档属性
| 名称 | 全等三角形复习学案(田畔中学黎汝华) |  | |
| 格式 | zip | ||
| 文件大小 | 119.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-20 20:43:42 | ||
图片预览

文档简介
《全等三角形》复习
一、知识归纳:
1、概念:
全等形:能够完全重合的图形叫做全等形。
全等三角形:能够完全重合的两个三角形叫做全等三角形。
把两个全等的三角形重合到一起,重合的顶点叫做对应顶点;重合的边叫做对应边;重合的角叫做对应角。
2、全等三角形的性质:全等三角形的对应边相等、对应角相等。
3、三角形全等的条件:
三边对应相等的两个三角形全等。 (可以简写成“边边边”或“SSS”)。
两边和它们的夹角对应相等的两个三角形全等。 (可以简写成“边角边”或“SAS”)。
两角和它们的夹边对应相等的两个三角形全等。 (可以简写成“角边角”或“ASA”)。
两个角和其中一个角的对边对应相等的两个三角形全等。 (可以简写成“角角边”或“AAS”)。
二、例题学习:
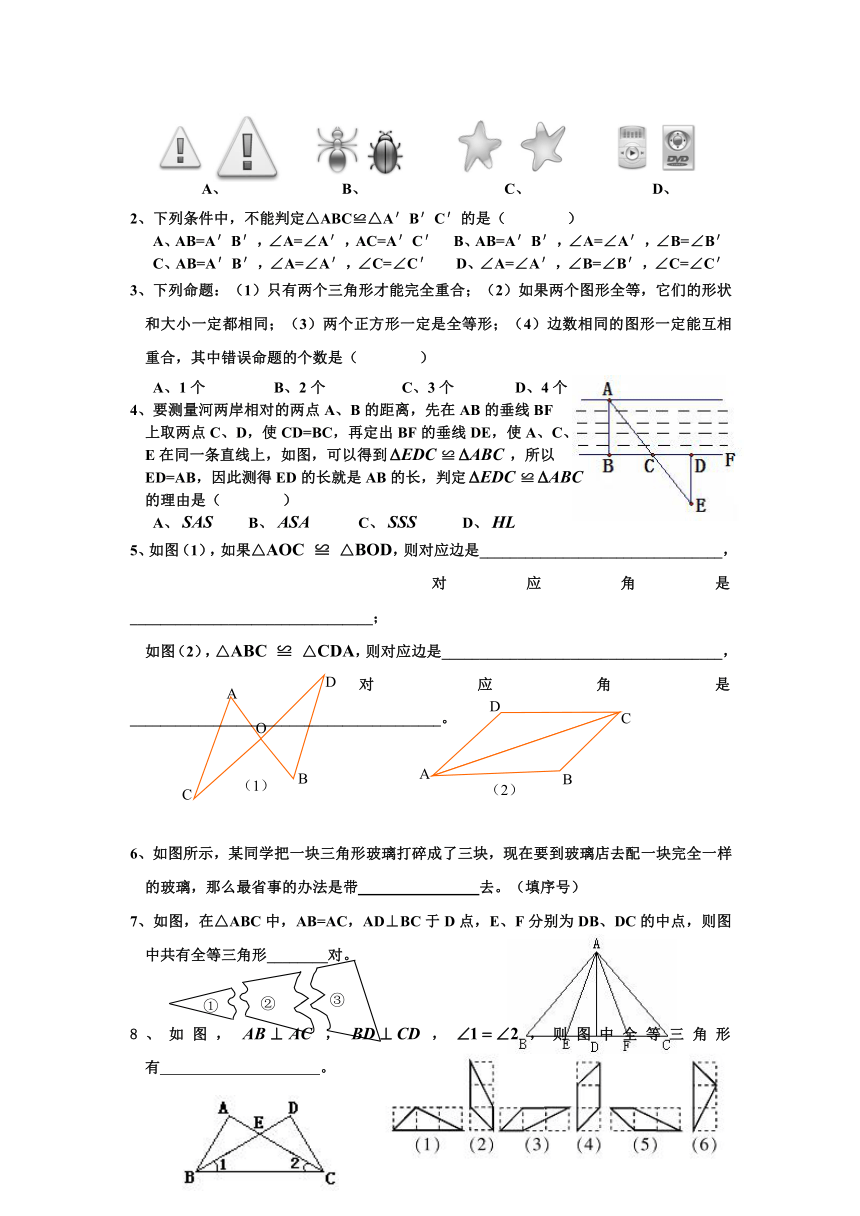
例1、如图,在△ABC和△DEF中,∠B=∠E,AB=DE。
(1)若加条件____________,可用SAS推得△ABC≌△ADE;
(2)若加条件____________,可用ASA推得△ABC≌△ADE;
(3)若加条件____________,可用AAS推得△ABC≌△ADE。
例2、如图,AB=DC,BE=CF,AF=DE,求证:AB∥DC。
例3、如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC面积是,,,求DE的长。
三、夯实基础:
1、在下列各组图形中,是全等的图形是( )
A、 B、 C、 D、
2、下列条件中,不能判定△ABC≌△A′B′C′的是( )
A、AB=A′B′,∠A=∠A′,AC=A′C′ B、AB=A′B′,∠A=∠A′,∠B=∠B′
C、AB=A′B′,∠A=∠A′,∠C=∠C′ D、∠A=∠A′,∠B=∠B′,∠C=∠C′
3、下列命题:(1)只有两个三角形才能完全重合;(2)如果两个图形全等,它们的形状和大小一定都相同;(3)两个正方形一定是全等形;(4)边数相同的图形一定能互相重合,其中错误命题的个数是( )
A、1个 B、2个 C、3个 D、4个
4、要测量河两岸相对的两点A、B的距离,先在AB的垂线BF
上取两点C、D,使CD=BC,再定出BF的垂线DE,使A、C、
E在同一条直线上,如图,可以得到≌,所以
ED=AB,因此测得ED的长就是AB的长,判定≌
的理由是( )
A、 B、 C、 D、
5、如图(1),如果△AOC ≌ △BOD,则对应边是________________________________,
对应角是________________________________;
如图(2),△ABC ≌ △CDA,则对应边是_____________________________________,
对应角是_________________________________________。
6、如图所示,某同学把一块三角形玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是带 去。(填序号)
7、如图,在△ABC中,AB=AC,AD⊥BC于D点,E、F分别为DB、DC的中点,则图中共有全等三角形________对。
8、如图,,,,则图中全等三角形有 。
9、如图中有6个条形方格图,图上由实线围成的图形是全等形的有 。
10、如图,△ABC是不等边三角形,DE=BC,以D ,E为两个顶点作位置不同的三角形,使所作的三角形与△ABC全等,这样的三角形最多可以画出_________个。
11、仔细填一填:
(1)如图1,已知:AC =DB,要使≌,只需增加一个条件是_____ ___。
(2)如图2,已知:中,,AM平分,,那么点M到AB的距离是 。
(3)如图3,已知:在和中,如果AB =DE,BC =EF,只要找出
= 或 = 或 // ,就可证得≌。
(4)已知:如图4,AB =EB,∠1=∠2,∠ADE =120°,AE、BD相交于F,则∠3的度数为 。
(5)如图5,已知:∠1 =∠2、∠3 =∠4,要证BD =CD ,需先证△AEB ≌△A EC ,根据是 ,再证△BDE ≌△ ,根据是 。
(6)已知:如图6 ,ACBC于C ,DEAC于E,ADAB于A ,BC =AE,
若AB = 5 ,则AD =___________。
12、如图,△ABC和△CDE都是等边三角形,求证:AD=BE。
13、如图,已知正方形,点是上的一点,连结,以为一边,在的上方作正方形,连结。
求证:。
C
O
B
D
A
D
C
B
A
(2)
(1)
②
①
③
A
B
D
F
E
C
图3
A
C
B
M
图2
A
O
D
C
图1
B
A
B
D
F
E
1
2
3
4
2
1
E
D
C
B
A
3
4
D
C
B
A
E
图6
图4
图5
E
B
C
G
D
F
A
一、知识归纳:
1、概念:
全等形:能够完全重合的图形叫做全等形。
全等三角形:能够完全重合的两个三角形叫做全等三角形。
把两个全等的三角形重合到一起,重合的顶点叫做对应顶点;重合的边叫做对应边;重合的角叫做对应角。
2、全等三角形的性质:全等三角形的对应边相等、对应角相等。
3、三角形全等的条件:
三边对应相等的两个三角形全等。 (可以简写成“边边边”或“SSS”)。
两边和它们的夹角对应相等的两个三角形全等。 (可以简写成“边角边”或“SAS”)。
两角和它们的夹边对应相等的两个三角形全等。 (可以简写成“角边角”或“ASA”)。
两个角和其中一个角的对边对应相等的两个三角形全等。 (可以简写成“角角边”或“AAS”)。
二、例题学习:
例1、如图,在△ABC和△DEF中,∠B=∠E,AB=DE。
(1)若加条件____________,可用SAS推得△ABC≌△ADE;
(2)若加条件____________,可用ASA推得△ABC≌△ADE;
(3)若加条件____________,可用AAS推得△ABC≌△ADE。
例2、如图,AB=DC,BE=CF,AF=DE,求证:AB∥DC。
例3、如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC面积是,,,求DE的长。
三、夯实基础:
1、在下列各组图形中,是全等的图形是( )
A、 B、 C、 D、
2、下列条件中,不能判定△ABC≌△A′B′C′的是( )
A、AB=A′B′,∠A=∠A′,AC=A′C′ B、AB=A′B′,∠A=∠A′,∠B=∠B′
C、AB=A′B′,∠A=∠A′,∠C=∠C′ D、∠A=∠A′,∠B=∠B′,∠C=∠C′
3、下列命题:(1)只有两个三角形才能完全重合;(2)如果两个图形全等,它们的形状和大小一定都相同;(3)两个正方形一定是全等形;(4)边数相同的图形一定能互相重合,其中错误命题的个数是( )
A、1个 B、2个 C、3个 D、4个
4、要测量河两岸相对的两点A、B的距离,先在AB的垂线BF
上取两点C、D,使CD=BC,再定出BF的垂线DE,使A、C、
E在同一条直线上,如图,可以得到≌,所以
ED=AB,因此测得ED的长就是AB的长,判定≌
的理由是( )
A、 B、 C、 D、
5、如图(1),如果△AOC ≌ △BOD,则对应边是________________________________,
对应角是________________________________;
如图(2),△ABC ≌ △CDA,则对应边是_____________________________________,
对应角是_________________________________________。
6、如图所示,某同学把一块三角形玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是带 去。(填序号)
7、如图,在△ABC中,AB=AC,AD⊥BC于D点,E、F分别为DB、DC的中点,则图中共有全等三角形________对。
8、如图,,,,则图中全等三角形有 。
9、如图中有6个条形方格图,图上由实线围成的图形是全等形的有 。
10、如图,△ABC是不等边三角形,DE=BC,以D ,E为两个顶点作位置不同的三角形,使所作的三角形与△ABC全等,这样的三角形最多可以画出_________个。
11、仔细填一填:
(1)如图1,已知:AC =DB,要使≌,只需增加一个条件是_____ ___。
(2)如图2,已知:中,,AM平分,,那么点M到AB的距离是 。
(3)如图3,已知:在和中,如果AB =DE,BC =EF,只要找出
= 或 = 或 // ,就可证得≌。
(4)已知:如图4,AB =EB,∠1=∠2,∠ADE =120°,AE、BD相交于F,则∠3的度数为 。
(5)如图5,已知:∠1 =∠2、∠3 =∠4,要证BD =CD ,需先证△AEB ≌△A EC ,根据是 ,再证△BDE ≌△ ,根据是 。
(6)已知:如图6 ,ACBC于C ,DEAC于E,ADAB于A ,BC =AE,
若AB = 5 ,则AD =___________。
12、如图,△ABC和△CDE都是等边三角形,求证:AD=BE。
13、如图,已知正方形,点是上的一点,连结,以为一边,在的上方作正方形,连结。
求证:。
C
O
B
D
A
D
C
B
A
(2)
(1)
②
①
③
A
B
D
F
E
C
图3
A
C
B
M
图2
A
O
D
C
图1
B
A
B
D
F
E
1
2
3
4
2
1
E
D
C
B
A
3
4
D
C
B
A
E
图6
图4
图5
E
B
C
G
D
F
A
