2020-2021学年人教版九年级下册数学 27.3位似图形课件(24张)
文档属性
| 名称 | 2020-2021学年人教版九年级下册数学 27.3位似图形课件(24张) |  | |
| 格式 | ppt | ||
| 文件大小 | 669.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-19 19:32:22 | ||
图片预览





文档简介
位似图形
27.3
在幻灯机放映图片的过程中,这些图片有什么关系呢?
P
一、感受新知,位似的定义
在幻灯机上放映幻灯片时,把幻灯片上的图象放大到屏幕上
在照相馆里,摄影师通过照相机把实物的图象缩小在底片上
这样放大或缩小的图形,形状_____,大小______,所以它们_____.
相同
不同
相似
放映机
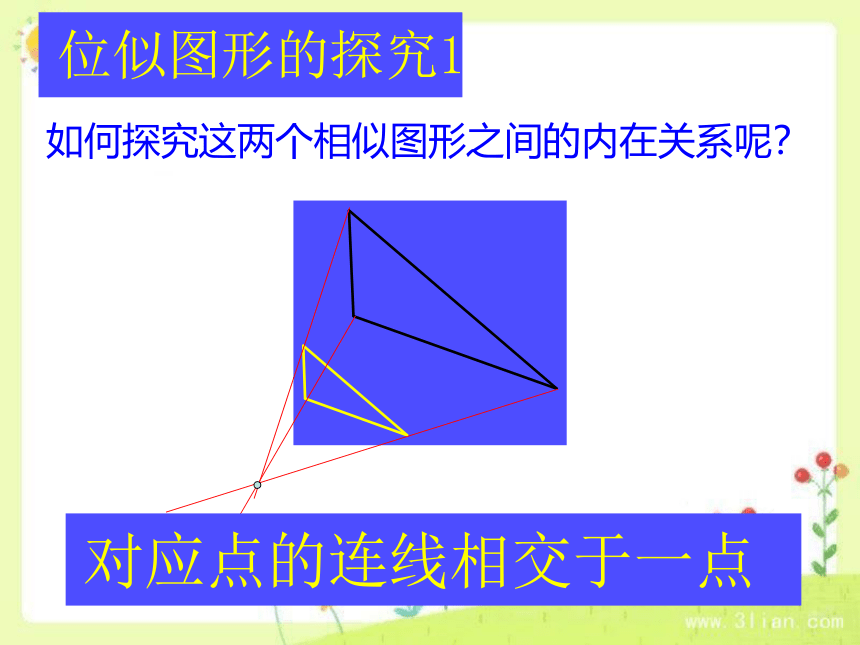
如何探究这两个相似图形之间的内在关系呢?
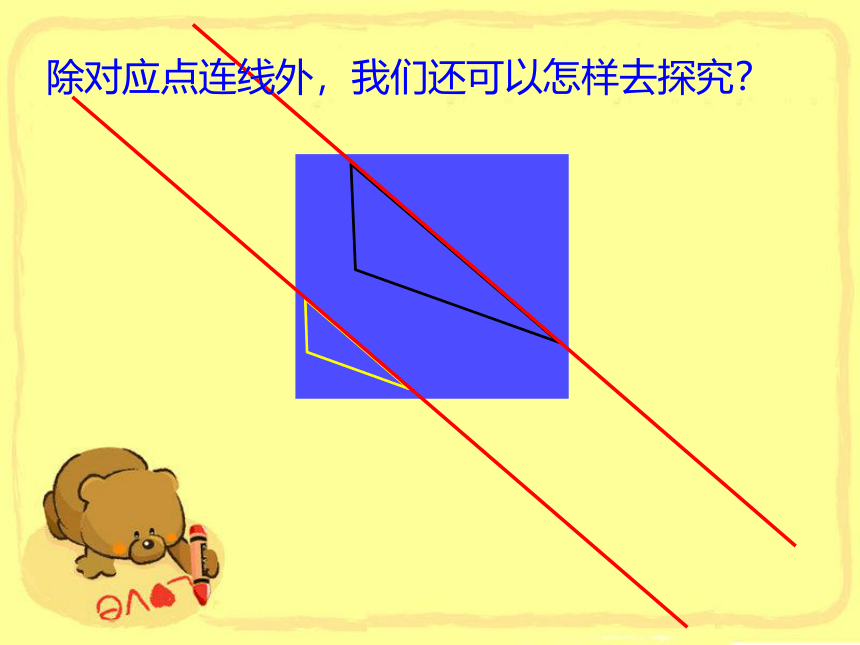
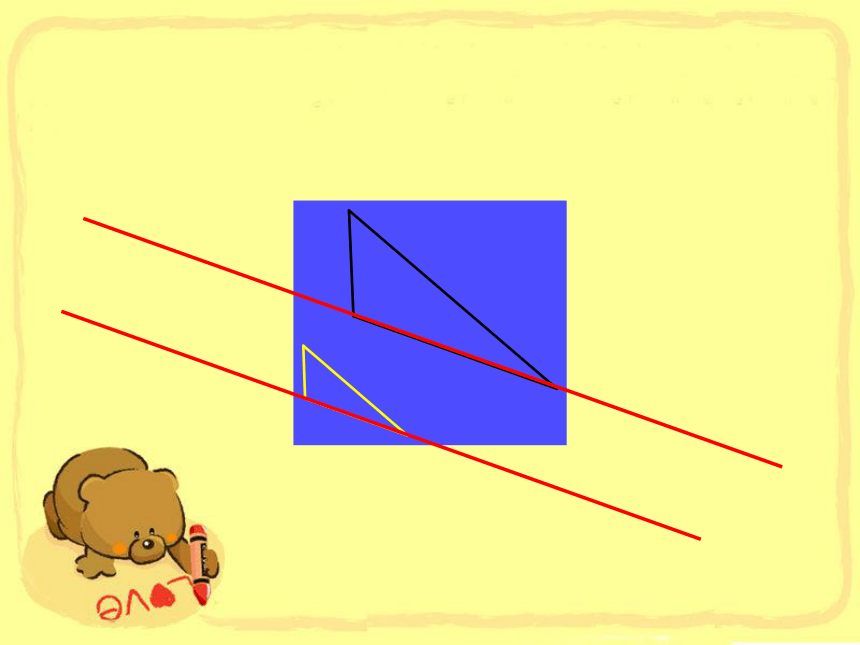
除对应点连线外,我们还可以怎样去探究?
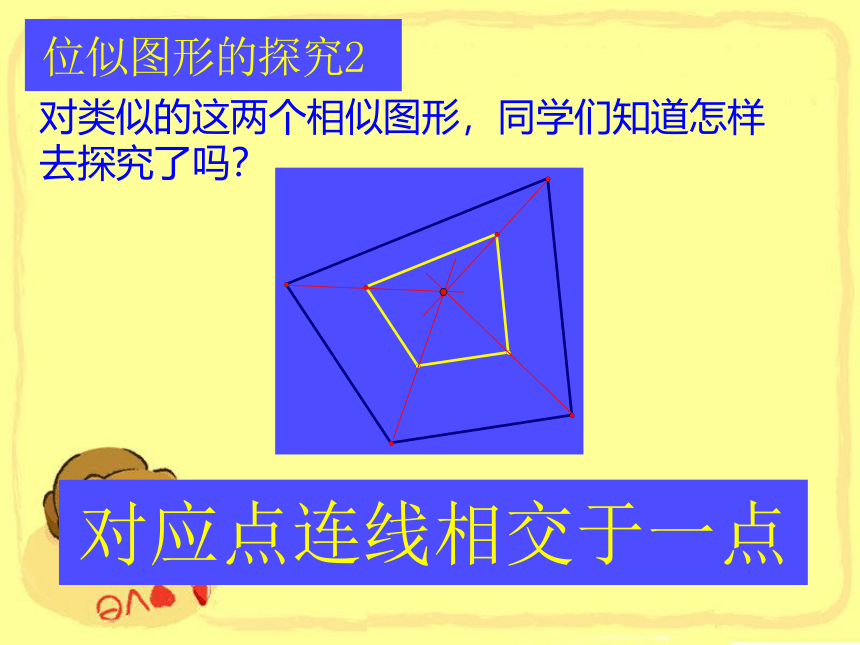
对类似的这两个相似图形,同学们知道怎样
去探究了吗?
根据经验,我们从对应边的位置关系去探究。
再探究这两个相似图形,对同学们来说已经不是难事了,我们完全有能力自己去探究!
知道了位似图形的特征,如何按要求去画位似图形呢?
知识要点总结
二、位似图形的画法
A
B
A’
C’
B’
C
O
以0为位似中心把△ABC
在同侧缩小为原来的一半。
1、画出ABC
2、选取中心点
3、连结OA、OB、OC。
4、在OA、OB、OC上分别选取A’、B’、C’,
使OA’/OA=1/2、OB’/OB=1/2、OC’/OC=1/2。
步骤:
5、连结A’B’C’,所连成的图形就是所求作图形。
二、位似图形的画法
A
B
A’
C’
B’
C
O
以0为中心把△ABC
缩小为原来的一半。
练习:如图:以O为位似中心,
将△ABC放大为原来的两倍
如果把位似图形放到直角体系中,又如何去探究位似变换与坐标之间的关系呢?
如图,在平面直角坐标系中,有两点A(6,3),B(6,0).以原点O为位似中心,相似比为 ,把线段AB缩小,观察对应点之间坐标的变化,你有什么发现?
x
y
2
4
6
8
2
4
6
8
-2
-4
-6
-8
-2
-4
-6
-8
O
A
B
A'
B'
A〞
B〞
位似变换后A,B的对应点为A ' ( , ),B'( , );A"( , ),B" ( , ).
2
1
2
0
- 2
- 1
- 2
0
三、位似变换与坐标的关系
x
y
2
4
6
8
2
4
6
8
-2
-4
-6
-8
-2
-4
-6
-8
O
9
10
11
12
-9
-10
-12
如图,△ABC三个顶点坐标分别为A(2,3),B(2,1),C(6,2),以点O为位似中心,相似比为2,将△ABC放大,观察对应顶点坐标的变化,你有什么发现?
A
B
C
位似变换后A,B,C的对应点为
A '( , ),B ' ( , ),C ' ( , );
A" ( , ),B" ( , ),C" ( , ).
4
6
4
2
12
4
-4
-6
-4
-2
-4
-12
A'
B'
C'
A"
B"
C"
在平面直角坐标系中,
如果位似变换是以原点为位似中心,
相似比为k,
那么位似图形对应点的坐标的比等于k或-k
归纳:
例 如图,四边形ABCD的坐标分别为A(-6,6),B(-8,2),C(-4,0),D(-2,4),画出它的一个以原点O为位似中心,相似比为 的位似图形.
分析:问题的关键是要确定位似图形各个顶点的坐标.根据前面的规律,点A的对应点A‘的坐标为 ,即(-3,3).类似地,可以确定其他顶点的坐标.
解:如图,利用位似变换中对应点的坐标的变化规律.分别取点
A'( , ),B ' ( , ),
C ' ( , ),D'( , ).
x
y
2
4
6
8
2
4
6
8
-2
-4
-6
-8
-2
-4
-6
-8
A
B
C
D
A'
B'
C'
D'
- 3
3
- 4
1
-2
0
-1
2
依次连接点A'B'C'D'就是要求的四边形ABCD的位似图形.
就这一个结果吗?
例:如果四边形ABCD的坐标分别为
A(-6,6),B(-8,2),C(-4,0),D(-2,4),
写出以原点为位似中心,相似比为(1/2)的
一个图形的对应点的坐标。
参考答案:
1、画出基本图形
2、选取位似中心
3、根据条件确定对应点,并描出对应点
4、顺次连结各对应点,所成的图形就是
所求的图形
一、定义及性质:
在平面直角坐标系中,如果位似变换
是以原点为位似中心,相似比为k,
那么位似图形对应点的坐标的比等于k或-k
课 堂 小 结
二、位似图形的画法:
三、位似变换与坐标的关系:
27.3
在幻灯机放映图片的过程中,这些图片有什么关系呢?
P
一、感受新知,位似的定义
在幻灯机上放映幻灯片时,把幻灯片上的图象放大到屏幕上
在照相馆里,摄影师通过照相机把实物的图象缩小在底片上
这样放大或缩小的图形,形状_____,大小______,所以它们_____.
相同
不同
相似
放映机
如何探究这两个相似图形之间的内在关系呢?
除对应点连线外,我们还可以怎样去探究?
对类似的这两个相似图形,同学们知道怎样
去探究了吗?
根据经验,我们从对应边的位置关系去探究。
再探究这两个相似图形,对同学们来说已经不是难事了,我们完全有能力自己去探究!
知道了位似图形的特征,如何按要求去画位似图形呢?
知识要点总结
二、位似图形的画法
A
B
A’
C’
B’
C
O
以0为位似中心把△ABC
在同侧缩小为原来的一半。
1、画出ABC
2、选取中心点
3、连结OA、OB、OC。
4、在OA、OB、OC上分别选取A’、B’、C’,
使OA’/OA=1/2、OB’/OB=1/2、OC’/OC=1/2。
步骤:
5、连结A’B’C’,所连成的图形就是所求作图形。
二、位似图形的画法
A
B
A’
C’
B’
C
O
以0为中心把△ABC
缩小为原来的一半。
练习:如图:以O为位似中心,
将△ABC放大为原来的两倍
如果把位似图形放到直角体系中,又如何去探究位似变换与坐标之间的关系呢?
如图,在平面直角坐标系中,有两点A(6,3),B(6,0).以原点O为位似中心,相似比为 ,把线段AB缩小,观察对应点之间坐标的变化,你有什么发现?
x
y
2
4
6
8
2
4
6
8
-2
-4
-6
-8
-2
-4
-6
-8
O
A
B
A'
B'
A〞
B〞
位似变换后A,B的对应点为A ' ( , ),B'( , );A"( , ),B" ( , ).
2
1
2
0
- 2
- 1
- 2
0
三、位似变换与坐标的关系
x
y
2
4
6
8
2
4
6
8
-2
-4
-6
-8
-2
-4
-6
-8
O
9
10
11
12
-9
-10
-12
如图,△ABC三个顶点坐标分别为A(2,3),B(2,1),C(6,2),以点O为位似中心,相似比为2,将△ABC放大,观察对应顶点坐标的变化,你有什么发现?
A
B
C
位似变换后A,B,C的对应点为
A '( , ),B ' ( , ),C ' ( , );
A" ( , ),B" ( , ),C" ( , ).
4
6
4
2
12
4
-4
-6
-4
-2
-4
-12
A'
B'
C'
A"
B"
C"
在平面直角坐标系中,
如果位似变换是以原点为位似中心,
相似比为k,
那么位似图形对应点的坐标的比等于k或-k
归纳:
例 如图,四边形ABCD的坐标分别为A(-6,6),B(-8,2),C(-4,0),D(-2,4),画出它的一个以原点O为位似中心,相似比为 的位似图形.
分析:问题的关键是要确定位似图形各个顶点的坐标.根据前面的规律,点A的对应点A‘的坐标为 ,即(-3,3).类似地,可以确定其他顶点的坐标.
解:如图,利用位似变换中对应点的坐标的变化规律.分别取点
A'( , ),B ' ( , ),
C ' ( , ),D'( , ).
x
y
2
4
6
8
2
4
6
8
-2
-4
-6
-8
-2
-4
-6
-8
A
B
C
D
A'
B'
C'
D'
- 3
3
- 4
1
-2
0
-1
2
依次连接点A'B'C'D'就是要求的四边形ABCD的位似图形.
就这一个结果吗?
例:如果四边形ABCD的坐标分别为
A(-6,6),B(-8,2),C(-4,0),D(-2,4),
写出以原点为位似中心,相似比为(1/2)的
一个图形的对应点的坐标。
参考答案:
1、画出基本图形
2、选取位似中心
3、根据条件确定对应点,并描出对应点
4、顺次连结各对应点,所成的图形就是
所求的图形
一、定义及性质:
在平面直角坐标系中,如果位似变换
是以原点为位似中心,相似比为k,
那么位似图形对应点的坐标的比等于k或-k
课 堂 小 结
二、位似图形的画法:
三、位似变换与坐标的关系:
