2020-2021学年八年级数学人教版下册:第17章勾股定理复习课课件(第一开课时 36张)
文档属性
| 名称 | 2020-2021学年八年级数学人教版下册:第17章勾股定理复习课课件(第一开课时 36张) |  | |
| 格式 | pptx | ||
| 文件大小 | 739.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-19 19:34:23 | ||
图片预览




文档简介
勾股定理复习
第一课时
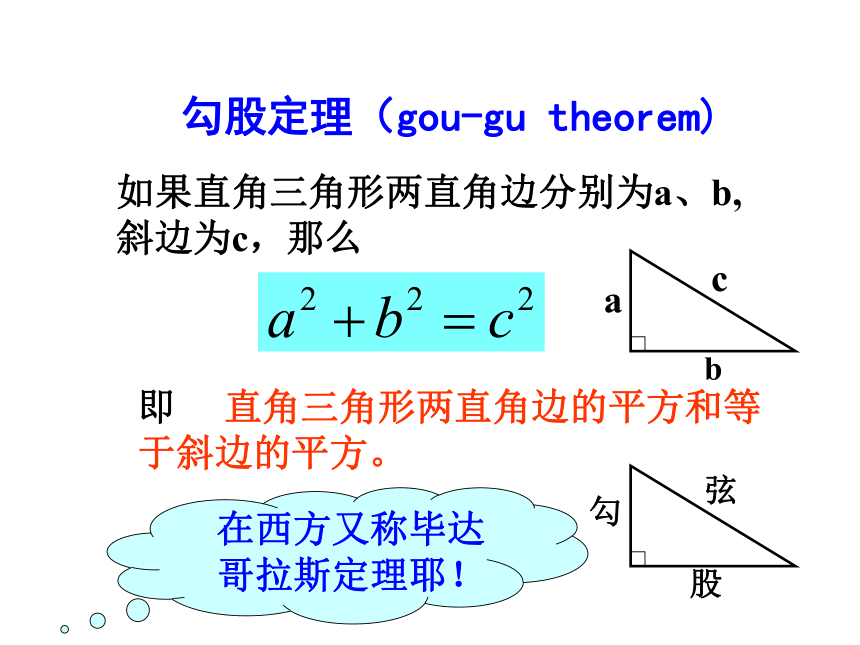
勾股定理(gou-gu theorem)
如果直角三角形两直角边分别为a、b,斜边为c,那么
即 直角三角形两直角边的平方和等于斜边的平方。
a
b
c
勾
股
弦
在西方又称毕达哥拉斯定理耶!
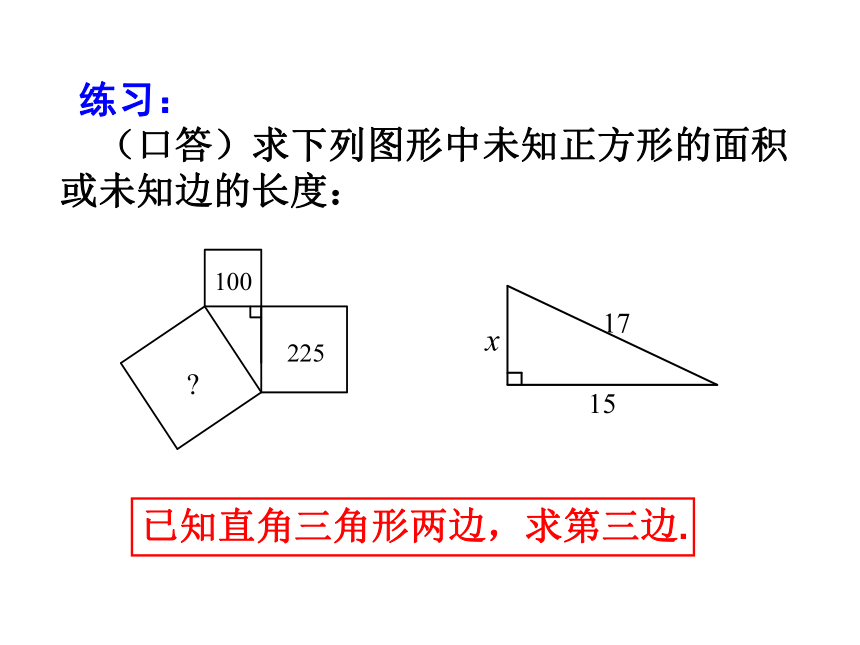
练习:
(口答)求下列图形中未知正方形的面积或未知边的长度:
已知直角三角形两边,求第三边.
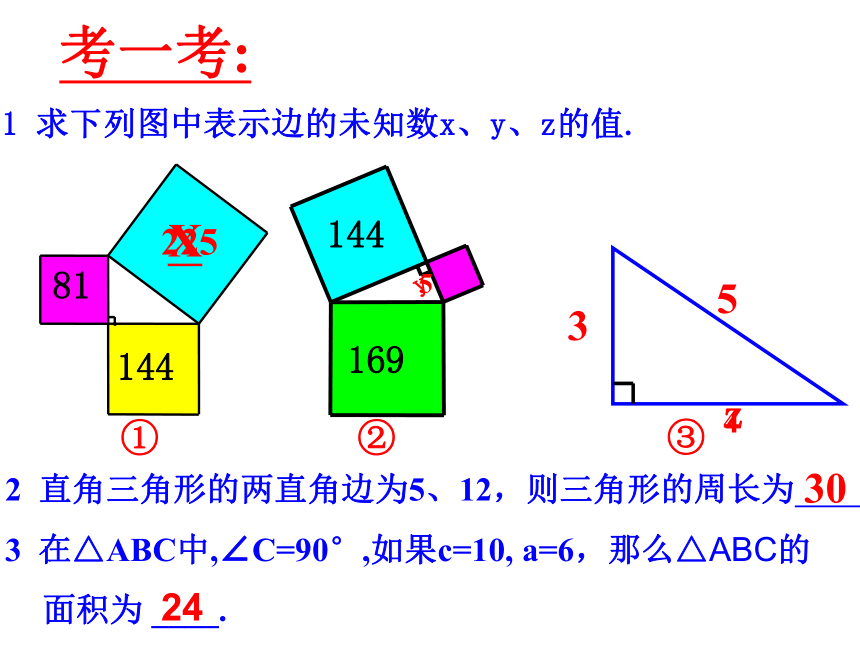
1 求下列图中表示边的未知数x、y、z的值.
①
81
144
y
z
②
③
144
169
3
5
考一考:
225
5
4
X
2 直角三角形的两直角边为5、12,则三角形的周长为 .
3 在△ABC中,∠C=90°,如果c=10, a=6,那么△ABC的
面积为 ____.
30
24
y=0
12
9
x
b
13
12
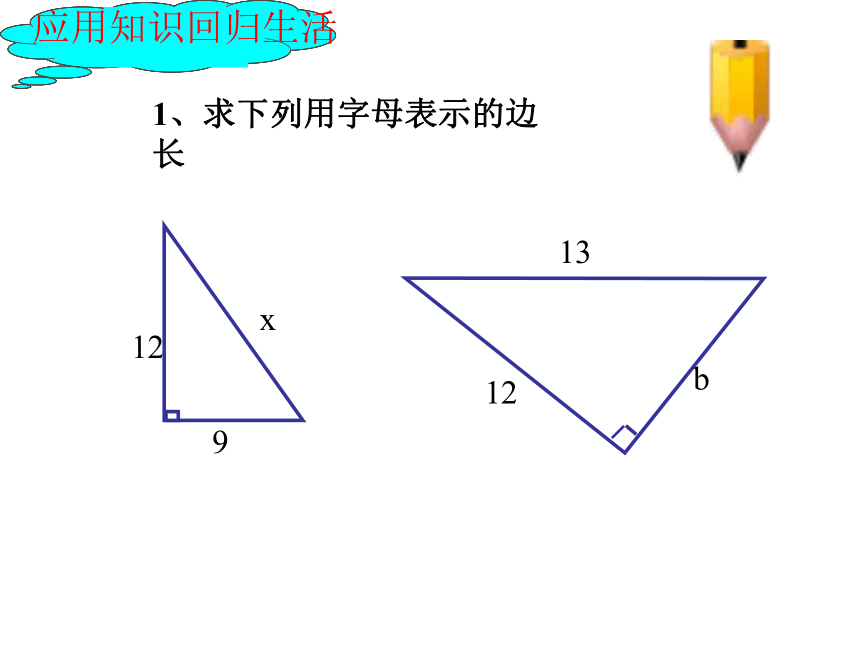
1、求下列用字母表示的边长
应用知识回归生活
那么这个三角形是直角三角形。
勾股定理的逆定理: 如果三角形的三边长a 、 b 、 c满足
A
B
C
a
b
c
1、小强想知道学校旗杆的高,他发现旗杆顶端的绳子垂到地面还多1米,当他把绳子的下端拉开5米后,发现下端刚好接触地面,你能帮他算出来吗?
A
B
C
5米
(x +1)米
x米
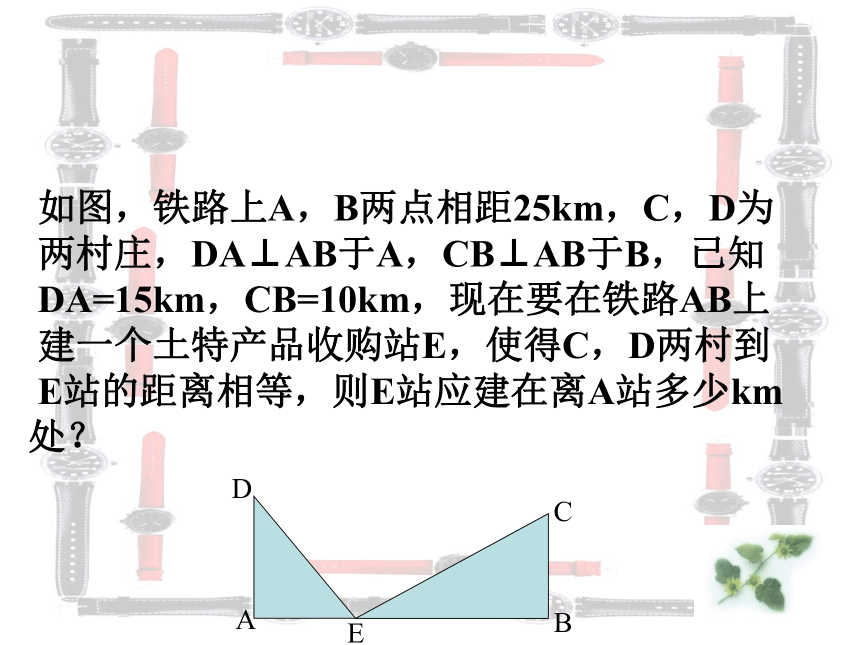
如图,铁路上A,B两点相距25km,C,D为
两村庄,DA⊥AB于A,CB⊥AB于B,已知
DA=15km,CB=10km,现在要在铁路AB上
建一个土特产品收购站E,使得C,D两村到
E站的距离相等,则E站应建在离A站多少km
处?
C
A
E
B
D
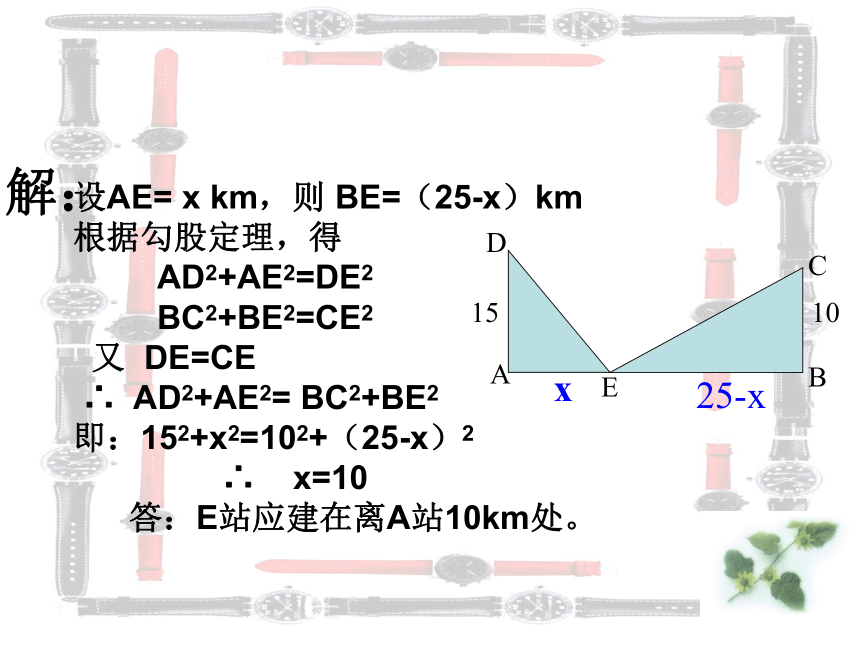
解:
设AE= x km,则 BE=(25-x)km
根据勾股定理,得
AD2+AE2=DE2
BC2+BE2=CE2
又 DE=CE
∴ AD2+AE2= BC2+BE2
即:152+x2=102+(25-x)2
∴ x=10
答:E站应建在离A站10km处。
x
25-x
C
A
E
B
D
15
10
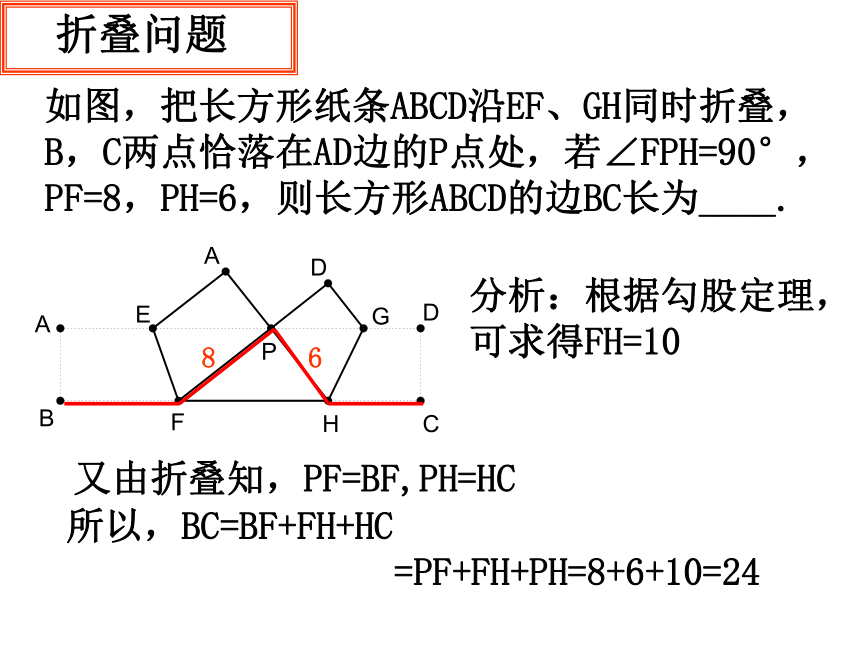
如图,把长方形纸条ABCD沿EF、GH同时折叠,
B,C两点恰落在AD边的P点处,若∠FPH=90°,
PF=8,PH=6,则长方形ABCD的边BC长为____.
分析:根据勾股定理,
可求得FH=10
又由折叠知,PF=BF,PH=HC
所以,BC=BF+FH+HC
=PF+FH+PH=8+6+10=24
8
6
折叠问题
如图,折叠长方形(四个角都是直角,对边相等)的一边,使点D落在BC边上的点F处,若AB=8,AD=10.
(1)你能说出图中哪些线段的长?
(2)求EC的长.
问题与思考
10
4
6
8
10
x
E
F
D
C
B
A
8-x
8-x
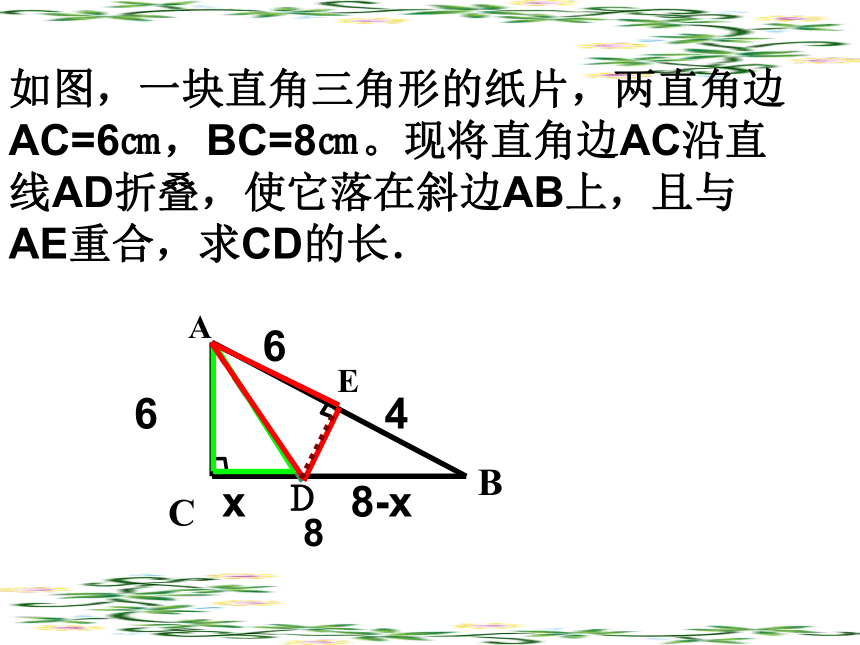
如图,一块直角三角形的纸片,两直角边AC=6㎝,BC=8㎝。现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,求CD的长.
A
C
B
E
第8题图
D
x
6
8-x
4
6
8
勾股定理复习
第二课时
1.下列各组数中,以a,b,c为边的三角形
不是Rt△的是( )
A、a=1.5,b=2,c=3 B、a=7,b=24,c=25
C、a=6,b=8,c=10 D a=3,b=4,c=5
2、下列各组数据能判断三角形是直角三角形的是( )
A、三边长都是2; B、三边长分别是3、4、3;
C、三边长分别是12、5、13;
D、三边长分别是7、4、5
选择题
选择题
3.已知一个Rt△的两边长分别为3和4,则第三
边长的平方是( )
A、25 B、14 C、7 D、7或25
D
4.如果Rt△两直角边的比为5∶12,则斜边上的
高与斜边的比为( )
A、60∶13 B、5∶12
C、12∶13 D、60∶169
D
6.等腰三角形底边上的高为8,周长为32,则三角形的面积为( )
A、56 B、48
C、40 D、32
5.如果Rt△的两直角边长分别为n2-1,2n(n>1), 那么它的斜边长是( )
A、2n B、n+1
C、n2-1 D、n2+1
D
选择题
7.若等腰三角形中相等的两边长为10cm,第三边长为16 cm,那么第三边上的高为 ( )
A. 12 cm B. 10 cm C. 8 cm D. 6 cm
8. 直角三角形的两条直角边长为a,b,斜边上的高为h,则下列各式中总能成立的是 ( )
选择题
9.已知Rt△ABC中,∠C=90°,若a+b=14cm,
c=10cm,则Rt△ABC的面积是( )
A、24cm2 B、36cm2 C、48cm2 D、60cm2
10.等腰三角形底边上的高为8,周长为32,则三
角形的面积为( )
A、56 B、48 C、40 D、32
A
B
选择题
11.有四个三角形,分别满足下列条件:
①一个内角等于另两个内角之和;
②三个角之比为3:4:5;
③三边长分别为7、24、25
④三边之比为5:12:13
其中直角三角形有( )
A、1个 B、2个 C、3个 D、4个
C
12.等腰三角形底边上的高为8,周长为32,
则三角形的面积为( )
A、56 B、48 C、40 D、32
B
A
C
D
8
x
x
16-x
x2+82=(16-x)2
x=6
BC=2x=12
B
13.若等腰三角形中相等的两边长为10cm,第三边长为16 cm,那么第三边上的高为 ( C )
A. 12 cm B. 10 cm C. 8 cm D. 6 cm
选择题
14.有四个三角形,分别满足下列条件:
①一个内角等于另两个内角之和;
②三个角之比为3:4:5;
③三边长分别为7、24、25
④三边之比为5:12:13
其中直角三角形有( )
A、1个 B、2个 C、3个 D、4个
C
15、在Rt△ABC中,∠C=90°,
①若a=5,b=12,则c=___________;
②若a=15,c=25,则b=___________;
③若c=61,b=60,则a=__________;
④若a∶b=3∶4,c=10则SRt△ABC=________。
16、直角三角形两直角边长分别为5和12,则它
斜边上的高为__________。
13
20
11
24
60/13
19、菱形的两条对角线长分别是6和8,
它的高为___
17、三角形的三边长分别为4、5、3,
则三角形的面积为
20、等边三角形的边长为6,则它的面积为
18、若直角三角形的两边长分别为5,12,
则第三边长为__
21.一根旗杆高8m,断裂后旗杆顶端落于旗杆底端4m处,旗杆的断裂处距离地面 ( )米
22.直角三角形的两条直角边分别是5cm,12cm,其斜边上的高是( )cm.
23.以直角三角形的两直角边所作正方形的面积分别是25和144,则斜边长是( )
1.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积之和为__________ cm2。
做一做
A
B
C
D
2、等腰三角形底边上的高为8,周长为32,求这个三角形的面积
8
X
16-X
D
A
B
C
解:设这个三角形为ABC,高为AD,设BD为X,则AB为(16-X),
由勾股定理得:
X2+82=(16-X)2
即X2+64=256-32X+X2
∴ X=6
∴ S?ABC=BC?AD/2=2 ?6 ?8/2=48
解答题
3.已知:如图,在Rt△ABC中,∠C=90°,BC=6, AC=8
求:斜边上的高CD.
C
A
B
D
解:由勾股定理知
AB2=AC2+BC2
=82+62=100
∴AB=10
由三角形面积公式
? · AC · BC= ? · AB · CD
∴CD=4.8
?
解答题
4. 一艘轮船以16海里/时的速度离开港口向东南方向,另一艘轮船在同时同地以12海里/时的速度向西南方向航行,它们离开港口一个半小时后相距多远?
答:AB=30海里
北
南
西
东
o
┓
A
B
5.如图,在四边形ABCD中,∠BAD =900,∠DBC = 900 , AD = 3,AB = 4,BC = 12, 求CD;
A
B
C
D
6.已知,如图,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,且∠A=90°,求四边形ABCD的面积。
7.观察下列表格:
……
列举
猜想
3、4、5
32=4+5
5、12、13
52=12+13
7、24、25
72=24+25
……
13、b、c
132=b+c
请你结合该表格及相关知识,求出b、c的值.
即b= ,c=
5
4
3
2
1
8.观察下列图形,正方形1的边长为7,则
正方形2、3、4、5的面积之和为多少?
规律:
S2+S3+S4+S5=
S1
9.正方形面积与勾股定理中的a2、b2、c2的相互转化
在直线l上依次摆放着七个正方形,已知斜放置
的三个正方形的面积分别是1,2,3,正放置的四个
的正方形的面积依次是S1、S2、S3、S4,则
S1+S2+S3+S4= 。
S1
S2
S3
S4
1
2
3
4
C
10.如图,一条河同一侧的两村庄A、B,其中A、B
到河岸最短距离分别为AC=1km,BD=2km,
CD=4cm,现欲在河岸上建一个水泵站向A、B
两村送水,当建在河岸上何处时,使到A、B两
村铺设水管总长度最短,并求出最短距离。
A
P
B
A′
D
E
1
2
4
1
1
4
5
11.如图,在正方形ABCD中,AB=4,AE=2, DF=1,
图中有几个直角三角形,你是如何判断的?
4
1
2
2
4
3
易知:△ABE,△DEF,△FCB均为Rt△
由勾股定理知
BE2=22+42=20,EF2=22+12=5,
BF2=32+42=25
∴BE2+EF2=BF2
∴ △BEF是Rt △
第一课时
勾股定理(gou-gu theorem)
如果直角三角形两直角边分别为a、b,斜边为c,那么
即 直角三角形两直角边的平方和等于斜边的平方。
a
b
c
勾
股
弦
在西方又称毕达哥拉斯定理耶!
练习:
(口答)求下列图形中未知正方形的面积或未知边的长度:
已知直角三角形两边,求第三边.
1 求下列图中表示边的未知数x、y、z的值.
①
81
144
y
z
②
③
144
169
3
5
考一考:
225
5
4
X
2 直角三角形的两直角边为5、12,则三角形的周长为 .
3 在△ABC中,∠C=90°,如果c=10, a=6,那么△ABC的
面积为 ____.
30
24
y=0
12
9
x
b
13
12
1、求下列用字母表示的边长
应用知识回归生活
那么这个三角形是直角三角形。
勾股定理的逆定理: 如果三角形的三边长a 、 b 、 c满足
A
B
C
a
b
c
1、小强想知道学校旗杆的高,他发现旗杆顶端的绳子垂到地面还多1米,当他把绳子的下端拉开5米后,发现下端刚好接触地面,你能帮他算出来吗?
A
B
C
5米
(x +1)米
x米
如图,铁路上A,B两点相距25km,C,D为
两村庄,DA⊥AB于A,CB⊥AB于B,已知
DA=15km,CB=10km,现在要在铁路AB上
建一个土特产品收购站E,使得C,D两村到
E站的距离相等,则E站应建在离A站多少km
处?
C
A
E
B
D
解:
设AE= x km,则 BE=(25-x)km
根据勾股定理,得
AD2+AE2=DE2
BC2+BE2=CE2
又 DE=CE
∴ AD2+AE2= BC2+BE2
即:152+x2=102+(25-x)2
∴ x=10
答:E站应建在离A站10km处。
x
25-x
C
A
E
B
D
15
10
如图,把长方形纸条ABCD沿EF、GH同时折叠,
B,C两点恰落在AD边的P点处,若∠FPH=90°,
PF=8,PH=6,则长方形ABCD的边BC长为____.
分析:根据勾股定理,
可求得FH=10
又由折叠知,PF=BF,PH=HC
所以,BC=BF+FH+HC
=PF+FH+PH=8+6+10=24
8
6
折叠问题
如图,折叠长方形(四个角都是直角,对边相等)的一边,使点D落在BC边上的点F处,若AB=8,AD=10.
(1)你能说出图中哪些线段的长?
(2)求EC的长.
问题与思考
10
4
6
8
10
x
E
F
D
C
B
A
8-x
8-x
如图,一块直角三角形的纸片,两直角边AC=6㎝,BC=8㎝。现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,求CD的长.
A
C
B
E
第8题图
D
x
6
8-x
4
6
8
勾股定理复习
第二课时
1.下列各组数中,以a,b,c为边的三角形
不是Rt△的是( )
A、a=1.5,b=2,c=3 B、a=7,b=24,c=25
C、a=6,b=8,c=10 D a=3,b=4,c=5
2、下列各组数据能判断三角形是直角三角形的是( )
A、三边长都是2; B、三边长分别是3、4、3;
C、三边长分别是12、5、13;
D、三边长分别是7、4、5
选择题
选择题
3.已知一个Rt△的两边长分别为3和4,则第三
边长的平方是( )
A、25 B、14 C、7 D、7或25
D
4.如果Rt△两直角边的比为5∶12,则斜边上的
高与斜边的比为( )
A、60∶13 B、5∶12
C、12∶13 D、60∶169
D
6.等腰三角形底边上的高为8,周长为32,则三角形的面积为( )
A、56 B、48
C、40 D、32
5.如果Rt△的两直角边长分别为n2-1,2n(n>1), 那么它的斜边长是( )
A、2n B、n+1
C、n2-1 D、n2+1
D
选择题
7.若等腰三角形中相等的两边长为10cm,第三边长为16 cm,那么第三边上的高为 ( )
A. 12 cm B. 10 cm C. 8 cm D. 6 cm
8. 直角三角形的两条直角边长为a,b,斜边上的高为h,则下列各式中总能成立的是 ( )
选择题
9.已知Rt△ABC中,∠C=90°,若a+b=14cm,
c=10cm,则Rt△ABC的面积是( )
A、24cm2 B、36cm2 C、48cm2 D、60cm2
10.等腰三角形底边上的高为8,周长为32,则三
角形的面积为( )
A、56 B、48 C、40 D、32
A
B
选择题
11.有四个三角形,分别满足下列条件:
①一个内角等于另两个内角之和;
②三个角之比为3:4:5;
③三边长分别为7、24、25
④三边之比为5:12:13
其中直角三角形有( )
A、1个 B、2个 C、3个 D、4个
C
12.等腰三角形底边上的高为8,周长为32,
则三角形的面积为( )
A、56 B、48 C、40 D、32
B
A
C
D
8
x
x
16-x
x2+82=(16-x)2
x=6
BC=2x=12
B
13.若等腰三角形中相等的两边长为10cm,第三边长为16 cm,那么第三边上的高为 ( C )
A. 12 cm B. 10 cm C. 8 cm D. 6 cm
选择题
14.有四个三角形,分别满足下列条件:
①一个内角等于另两个内角之和;
②三个角之比为3:4:5;
③三边长分别为7、24、25
④三边之比为5:12:13
其中直角三角形有( )
A、1个 B、2个 C、3个 D、4个
C
15、在Rt△ABC中,∠C=90°,
①若a=5,b=12,则c=___________;
②若a=15,c=25,则b=___________;
③若c=61,b=60,则a=__________;
④若a∶b=3∶4,c=10则SRt△ABC=________。
16、直角三角形两直角边长分别为5和12,则它
斜边上的高为__________。
13
20
11
24
60/13
19、菱形的两条对角线长分别是6和8,
它的高为___
17、三角形的三边长分别为4、5、3,
则三角形的面积为
20、等边三角形的边长为6,则它的面积为
18、若直角三角形的两边长分别为5,12,
则第三边长为__
21.一根旗杆高8m,断裂后旗杆顶端落于旗杆底端4m处,旗杆的断裂处距离地面 ( )米
22.直角三角形的两条直角边分别是5cm,12cm,其斜边上的高是( )cm.
23.以直角三角形的两直角边所作正方形的面积分别是25和144,则斜边长是( )
1.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积之和为__________ cm2。
做一做
A
B
C
D
2、等腰三角形底边上的高为8,周长为32,求这个三角形的面积
8
X
16-X
D
A
B
C
解:设这个三角形为ABC,高为AD,设BD为X,则AB为(16-X),
由勾股定理得:
X2+82=(16-X)2
即X2+64=256-32X+X2
∴ X=6
∴ S?ABC=BC?AD/2=2 ?6 ?8/2=48
解答题
3.已知:如图,在Rt△ABC中,∠C=90°,BC=6, AC=8
求:斜边上的高CD.
C
A
B
D
解:由勾股定理知
AB2=AC2+BC2
=82+62=100
∴AB=10
由三角形面积公式
? · AC · BC= ? · AB · CD
∴CD=4.8
?
解答题
4. 一艘轮船以16海里/时的速度离开港口向东南方向,另一艘轮船在同时同地以12海里/时的速度向西南方向航行,它们离开港口一个半小时后相距多远?
答:AB=30海里
北
南
西
东
o
┓
A
B
5.如图,在四边形ABCD中,∠BAD =900,∠DBC = 900 , AD = 3,AB = 4,BC = 12, 求CD;
A
B
C
D
6.已知,如图,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,且∠A=90°,求四边形ABCD的面积。
7.观察下列表格:
……
列举
猜想
3、4、5
32=4+5
5、12、13
52=12+13
7、24、25
72=24+25
……
13、b、c
132=b+c
请你结合该表格及相关知识,求出b、c的值.
即b= ,c=
5
4
3
2
1
8.观察下列图形,正方形1的边长为7,则
正方形2、3、4、5的面积之和为多少?
规律:
S2+S3+S4+S5=
S1
9.正方形面积与勾股定理中的a2、b2、c2的相互转化
在直线l上依次摆放着七个正方形,已知斜放置
的三个正方形的面积分别是1,2,3,正放置的四个
的正方形的面积依次是S1、S2、S3、S4,则
S1+S2+S3+S4= 。
S1
S2
S3
S4
1
2
3
4
C
10.如图,一条河同一侧的两村庄A、B,其中A、B
到河岸最短距离分别为AC=1km,BD=2km,
CD=4cm,现欲在河岸上建一个水泵站向A、B
两村送水,当建在河岸上何处时,使到A、B两
村铺设水管总长度最短,并求出最短距离。
A
P
B
A′
D
E
1
2
4
1
1
4
5
11.如图,在正方形ABCD中,AB=4,AE=2, DF=1,
图中有几个直角三角形,你是如何判断的?
4
1
2
2
4
3
易知:△ABE,△DEF,△FCB均为Rt△
由勾股定理知
BE2=22+42=20,EF2=22+12=5,
BF2=32+42=25
∴BE2+EF2=BF2
∴ △BEF是Rt △
