5.2 二次函数的图像和性质(第4课时)课件(共22张PPT)
文档属性
| 名称 | 5.2 二次函数的图像和性质(第4课时)课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-19 00:00:00 | ||
图片预览




文档简介
(共21张PPT)
5.2 二次函数的图像和性质
(第4课时)
第5章 二次函数
2020-2021学年度苏科版九年级下册
二次函数的图像和性质
0
x
y
y=ax2 a>0 a<0
二次函数y=ax2的性质
位置
开口方向
对称性
顶点
最值
增减性
开口向上在x轴上方
开口向下在x轴下方
a的绝对值越大,开口越小
关于y轴对称,对称轴方程是直线x=0
顶点坐标是原点(0,0)
当x=0时,y最小值=0
当x=0时,y最大值=0
在对称轴左侧递减
在对称轴右侧递增
在对称轴左侧递增
在对称轴右侧递减
复习与回忆
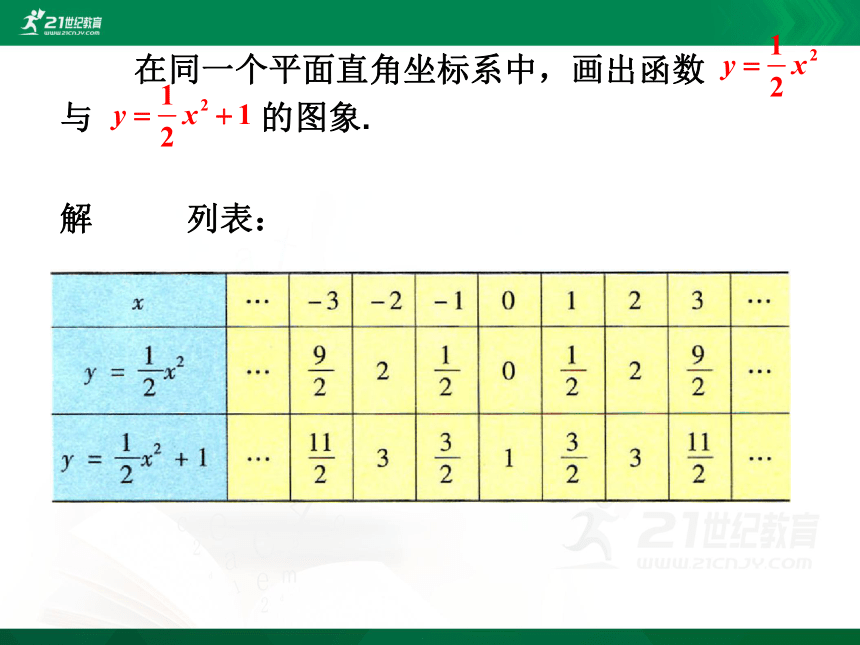
在同一个平面直角坐标系中,画出函数 与 的图象.
解 列表:
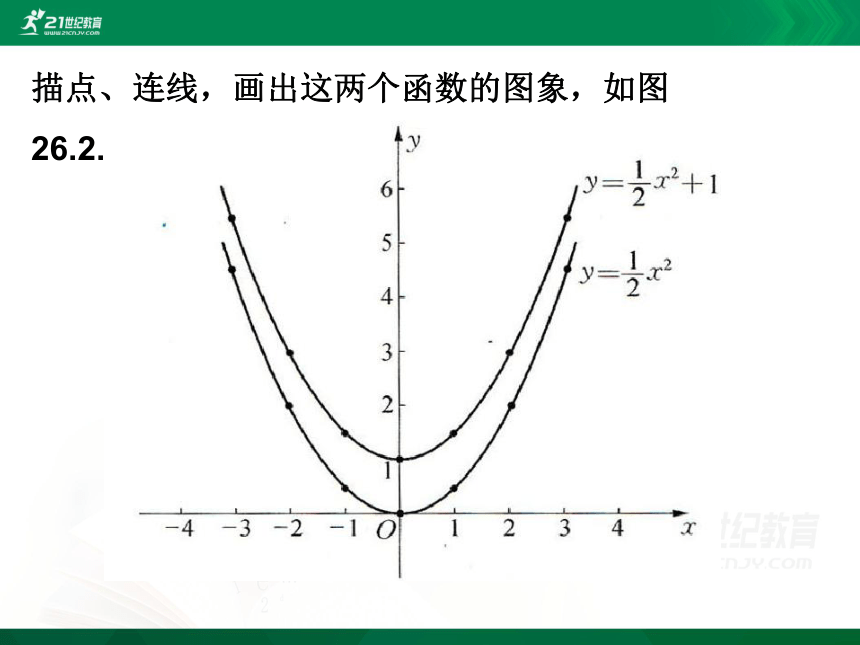
描点、连线,画出这两个函数的图象,如图26.2.2所示.
(1)二次函数 y=2x +1 的图象与二次函数 y=2x 的图象有什么关系?
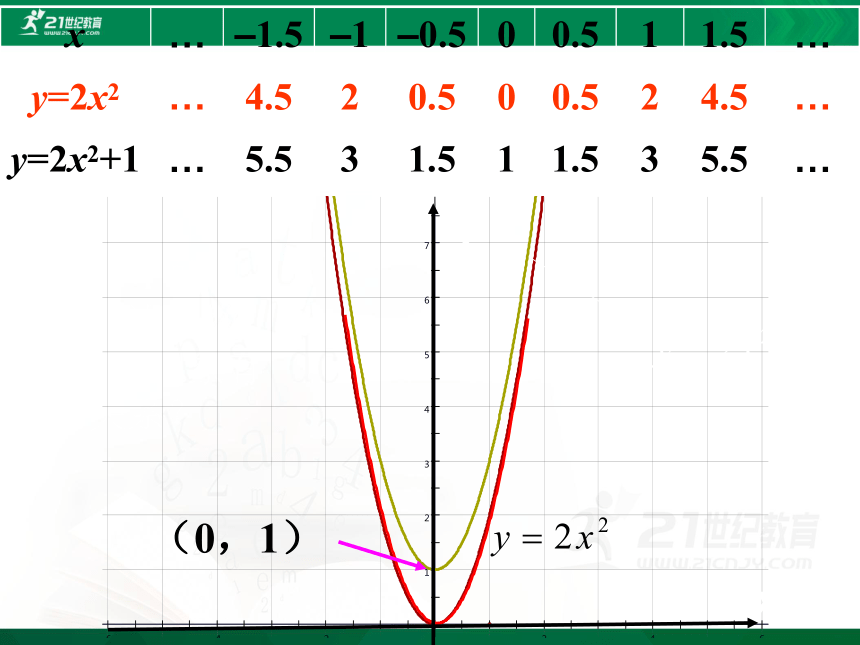
x … –1.5 –1 –0.5 0 0.5 1 1.5 …
y=2x2 … 4.5 2 0.5 0 0.5 2 4.5 …
y=2x2+1 … 5.5 3 1.5 1 1.5 3 5.5 …
(0,1)
x
y
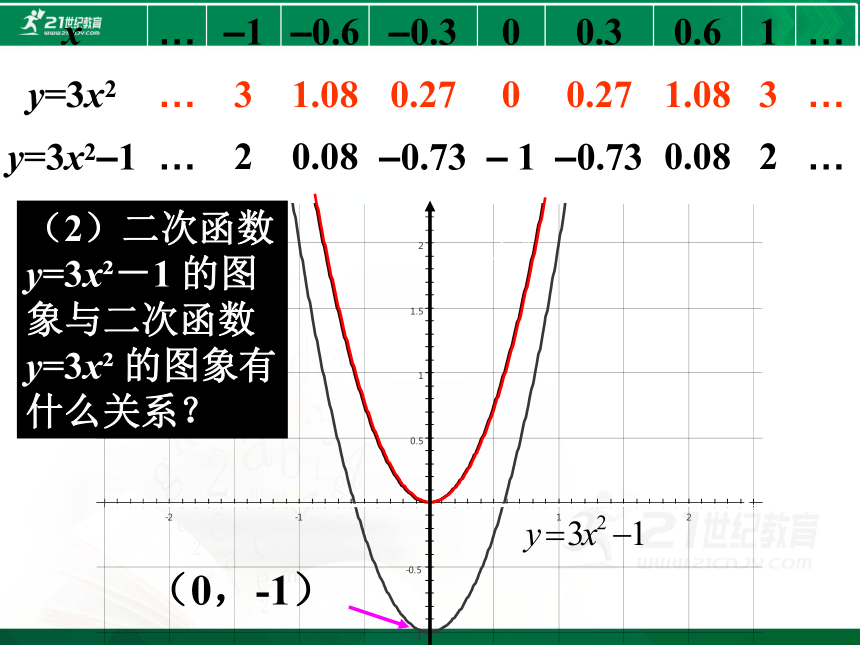
x … –1 –0.6 –0.3 0 0.3 0.6 1 …
y=3x2 … 3 1.08 0.27 0 0.27 1.08 3 …
y=3x2–1 … 2 0.08 –0.73 – 1 –0.73 0.08 2 …
(0,-1)
(2)二次函数 y=3x -1 的图象与二次函数 y=3x 的图象有什么关系?
y=ax2+k a>0 a<0
二次函数y=ax2+k的性质
位置开口方向
对称性
顶点
最值
增减性
开口向上
开口向下
a的绝对值越大,开口越小
关于y轴对称,对称轴方程是直线x=0
顶点坐标是原点(0,k)
当x=0时,y最小值=k
当x=0时,y最大值=k
在对称轴左侧递减
在对称轴右侧递增
在对称轴左侧递增
在对称轴右侧递减
开口大小
练习
1.把抛物线 向下平移2个单位,可以得到抛物线 ,再向上平移5个单位,可以得到抛物线 ;
2.对于函数y= –x2+1,当x 时,函数值y随x的增大而增大;当x 时,函数值y随x的增大而减小;当x 时,函数取得最 值,为 .
<0
>0
=0
大
1
3.把抛物线y=2x2向上平移5个单位.会得到哪条抛物线?向下平移3.4个单位呢?
4.把抛物线y=-4x2向上平移5个单位.会得到哪条抛物线?向下平移3.4个单位呢?
抛物线的开口方向,对称轴,顶点各是什么?
抛物线的开口方向,对称轴,顶点各是什么?
在如图26.2.3所示的平面直角坐标系中,画出函数 与 的图象.
解 列表:
描点、连线,画出这两个函数的图象.
图象是轴对称图形.
对称轴是平行于
y轴的直线:x= -1.
顶点坐标
是点(-1,0).
二次函数y=3(x+1)2
与y=3x2的图象形状
相同,可以看作是抛
物线y=3x2整体沿x轴
向左平移了1 个单位.
1.函数y=3(x+1)2的图象与y=3x2和y=3(x-1)2的图象有什么关系 它的对称轴和顶点坐标分别是什么
顶点坐标
是点(1,0).
图象是轴对称图形.
对称轴是平行于
y轴的直线:x= 1.
在对称轴(直线:x=-1)左侧
(即x<-1时),函数y=3(x+1)2
的值随x的增大而减少,.
顶点是最低点,
函数有最小值.
当x=-1时,
最小值是0..
二次函数y=3(x+1)2
与y=3x2的增减性类似.
2.x取哪些值时,函数y=3(x+1)2的值随x值的增大而增大 x取哪些值时,函数y=3(x+1)2的值随x的增大而减少?
在对称轴(直线:x
=-1)右侧(即x>-1
时),函数y=3(x+1)2
的值随x的增大而
增大,.
请你总结二次函数y=a(x-h)2的图象和性质.
(1)完成下表.
x -3 -2 -1 0 1 2 3 4
y=2x2
y=2(x-1)2
画二次函数y=2(x-1)2的图象.
18 8 2 0 2 8 18 32
32 18 8 2 0 2 8 18
y=2(x-1)2
y=2x2
(2)在坐标系中作出y=2(x-1)2的图象.
二次函数y=a(x-h)2的性质
1.顶点坐标与对称轴
2.位置与开口方向
3.增减性与最值
开口大小 抛物线
顶点坐标
对称轴
位置
开口方向
增减性
最值
y=a(x-h)2 (a>0)
y=a(x-h)2 (a<0)
(h,0)
(h,0)
直线x=h
直线x=h
在x轴的上方(除顶点外)
在x轴的下方( 除顶点外)
向上
向下
当x=h时,最小值为0.
当x=h时,最大值为0.
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
根据图形填表:
越小,开口越大.
越大,开口越小.
当a<0时,抛物线 的开口方向是 ,顶点坐标是( , ),对
称轴是 ,当x= 时,函数 取得最 值 ,y最 = .
1.当a>0时,抛物线 的开口方向是 ,顶点坐标是( , ),对
称轴是 ,当x= 时,函数 取得最 值 ,y最 = .
y=a(x+h)2
向上
-h
0
x=-h
-h
y=a(x+h)2
小
小值
0
y=a(x+h)2
向下
-h
0
x=-h
-h
y=a(x+h)2
大
大值
0
2.抛物线y=4(x-1)2可由抛物线y=4x2怎样平移后得到?
解:
抛物线y=4(x-1)2可由抛物线y=4x2向右平移1个单位后得到.
3.抛物线y=a(x+b)2的顶点为(-2,0),形状与抛物线y=5x2相同,但开口方向相反.
(1)求抛物线对应的函数表达式;
(2)求抛物线与y轴的交点坐标.
解:
(1)抛物线对应的函数表达式为:
y=-5(x+2)2
(2)抛物线与y轴的交点坐标为:
(0,-20)
谢谢聆听
5.2 二次函数的图像和性质
(第4课时)
第5章 二次函数
2020-2021学年度苏科版九年级下册
二次函数的图像和性质
0
x
y
y=ax2 a>0 a<0
二次函数y=ax2的性质
位置
开口方向
对称性
顶点
最值
增减性
开口向上在x轴上方
开口向下在x轴下方
a的绝对值越大,开口越小
关于y轴对称,对称轴方程是直线x=0
顶点坐标是原点(0,0)
当x=0时,y最小值=0
当x=0时,y最大值=0
在对称轴左侧递减
在对称轴右侧递增
在对称轴左侧递增
在对称轴右侧递减
复习与回忆
在同一个平面直角坐标系中,画出函数 与 的图象.
解 列表:
描点、连线,画出这两个函数的图象,如图26.2.2所示.
(1)二次函数 y=2x +1 的图象与二次函数 y=2x 的图象有什么关系?
x … –1.5 –1 –0.5 0 0.5 1 1.5 …
y=2x2 … 4.5 2 0.5 0 0.5 2 4.5 …
y=2x2+1 … 5.5 3 1.5 1 1.5 3 5.5 …
(0,1)
x
y
x … –1 –0.6 –0.3 0 0.3 0.6 1 …
y=3x2 … 3 1.08 0.27 0 0.27 1.08 3 …
y=3x2–1 … 2 0.08 –0.73 – 1 –0.73 0.08 2 …
(0,-1)
(2)二次函数 y=3x -1 的图象与二次函数 y=3x 的图象有什么关系?
y=ax2+k a>0 a<0
二次函数y=ax2+k的性质
位置开口方向
对称性
顶点
最值
增减性
开口向上
开口向下
a的绝对值越大,开口越小
关于y轴对称,对称轴方程是直线x=0
顶点坐标是原点(0,k)
当x=0时,y最小值=k
当x=0时,y最大值=k
在对称轴左侧递减
在对称轴右侧递增
在对称轴左侧递增
在对称轴右侧递减
开口大小
练习
1.把抛物线 向下平移2个单位,可以得到抛物线 ,再向上平移5个单位,可以得到抛物线 ;
2.对于函数y= –x2+1,当x 时,函数值y随x的增大而增大;当x 时,函数值y随x的增大而减小;当x 时,函数取得最 值,为 .
<0
>0
=0
大
1
3.把抛物线y=2x2向上平移5个单位.会得到哪条抛物线?向下平移3.4个单位呢?
4.把抛物线y=-4x2向上平移5个单位.会得到哪条抛物线?向下平移3.4个单位呢?
抛物线的开口方向,对称轴,顶点各是什么?
抛物线的开口方向,对称轴,顶点各是什么?
在如图26.2.3所示的平面直角坐标系中,画出函数 与 的图象.
解 列表:
描点、连线,画出这两个函数的图象.
图象是轴对称图形.
对称轴是平行于
y轴的直线:x= -1.
顶点坐标
是点(-1,0).
二次函数y=3(x+1)2
与y=3x2的图象形状
相同,可以看作是抛
物线y=3x2整体沿x轴
向左平移了1 个单位.
1.函数y=3(x+1)2的图象与y=3x2和y=3(x-1)2的图象有什么关系 它的对称轴和顶点坐标分别是什么
顶点坐标
是点(1,0).
图象是轴对称图形.
对称轴是平行于
y轴的直线:x= 1.
在对称轴(直线:x=-1)左侧
(即x<-1时),函数y=3(x+1)2
的值随x的增大而减少,.
顶点是最低点,
函数有最小值.
当x=-1时,
最小值是0..
二次函数y=3(x+1)2
与y=3x2的增减性类似.
2.x取哪些值时,函数y=3(x+1)2的值随x值的增大而增大 x取哪些值时,函数y=3(x+1)2的值随x的增大而减少?
在对称轴(直线:x
=-1)右侧(即x>-1
时),函数y=3(x+1)2
的值随x的增大而
增大,.
请你总结二次函数y=a(x-h)2的图象和性质.
(1)完成下表.
x -3 -2 -1 0 1 2 3 4
y=2x2
y=2(x-1)2
画二次函数y=2(x-1)2的图象.
18 8 2 0 2 8 18 32
32 18 8 2 0 2 8 18
y=2(x-1)2
y=2x2
(2)在坐标系中作出y=2(x-1)2的图象.
二次函数y=a(x-h)2的性质
1.顶点坐标与对称轴
2.位置与开口方向
3.增减性与最值
开口大小 抛物线
顶点坐标
对称轴
位置
开口方向
增减性
最值
y=a(x-h)2 (a>0)
y=a(x-h)2 (a<0)
(h,0)
(h,0)
直线x=h
直线x=h
在x轴的上方(除顶点外)
在x轴的下方( 除顶点外)
向上
向下
当x=h时,最小值为0.
当x=h时,最大值为0.
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
根据图形填表:
越小,开口越大.
越大,开口越小.
当a<0时,抛物线 的开口方向是 ,顶点坐标是( , ),对
称轴是 ,当x= 时,函数 取得最 值 ,y最 = .
1.当a>0时,抛物线 的开口方向是 ,顶点坐标是( , ),对
称轴是 ,当x= 时,函数 取得最 值 ,y最 = .
y=a(x+h)2
向上
-h
0
x=-h
-h
y=a(x+h)2
小
小值
0
y=a(x+h)2
向下
-h
0
x=-h
-h
y=a(x+h)2
大
大值
0
2.抛物线y=4(x-1)2可由抛物线y=4x2怎样平移后得到?
解:
抛物线y=4(x-1)2可由抛物线y=4x2向右平移1个单位后得到.
3.抛物线y=a(x+b)2的顶点为(-2,0),形状与抛物线y=5x2相同,但开口方向相反.
(1)求抛物线对应的函数表达式;
(2)求抛物线与y轴的交点坐标.
解:
(1)抛物线对应的函数表达式为:
y=-5(x+2)2
(2)抛物线与y轴的交点坐标为:
(0,-20)
谢谢聆听
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
