5.5 用二次函数解决问题(第2课时)课件(共23张PPT)
文档属性
| 名称 | 5.5 用二次函数解决问题(第2课时)课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-19 16:27:16 | ||
图片预览








文档简介
5.5 用二次函数解决问题
(第2课时)
第5章 二次函数
2020-2021学年度苏科版九年级下册
二次函数的图象与x轴有没有交点,由什么决定?
复习思考
由b?-4ac的符号决定
b?-4ac﹥0,有两个交点
b?-4ac=0,只有一个交点
b?-4ac﹤0,没有交点
求出二次函数y=10x-5x?图象的顶点坐标,与x轴的交点坐标,并画出函数的大致图象
启明公司生产某种产品,每件产品成本是3元,售价是4元,年销售量是10万件,为了获得更好的效益,公司准备拿出一定的资金做广告,根据经验,每年投入的广告费是x(万元)时,产品的年销售量将是原销售量的y倍,且y=﹣ x2+ x+ ,如果把利润看作是销售总额减去成本费和广告费:
⑴试写出年利润s(万元)与广告费x(万元)的函数关系式,并计算广告费是多少万元时,公司获得的年利润最大及最大年利润是多少万元.
解:⑴S=10×( )×(4-3)-x=-x2+6x+7
当x= =3时,
S最大= = = =16
∴当广告费是3万元时,公司获得的最大年利益是16万元.
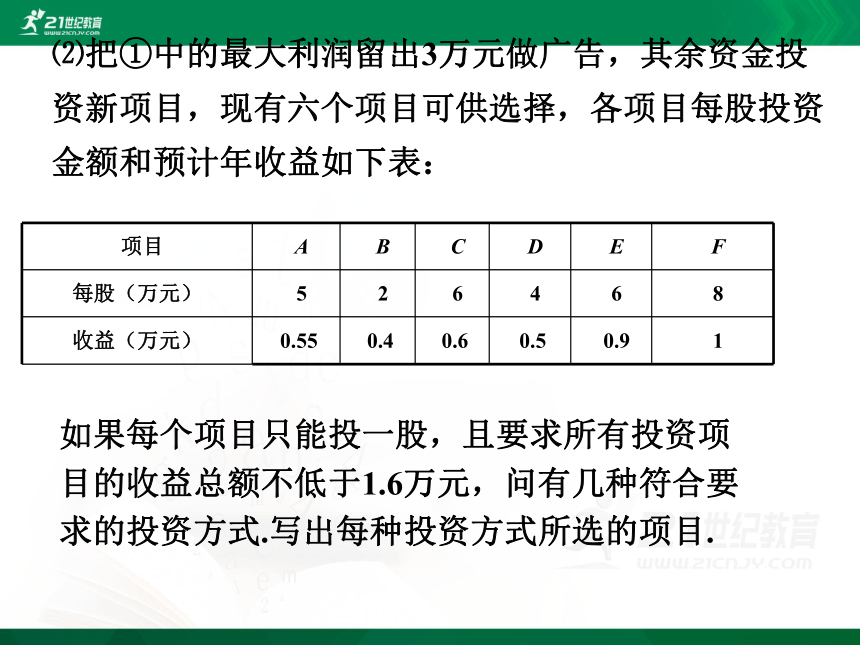
⑵把①中的最大利润留出3万元做广告,其余资金投资新项目,现有六个项目可供选择,各项目每股投资金额和预计年收益如下表:
项目
A
B
C
D
E
F
每股(万元)
5
2
6
4
6
8
收益(万元)
0.55
0.4
0.6
0.5
0.9
1
如果每个项目只能投一股,且要求所有投资项目的收益总额不低于1.6万元,问有几种符合要求的投资方式.写出每种投资方式所选的项目.
心理学家发现,通常情况下,学生对知识的接受能力y与学习知识所用的连续时间xmin之间满足函数关系
,
y的值越大,表示接受能力越强.
(1)x在什么范围内,学生的接受能力逐步增强?x又在什么范围内,学生的接受能力逐步降低?
解:观察函数关系式可知该函数是一条开口向下的抛物线,所以当x在对称轴左侧时,y逐步递增,当x在对称轴右侧时,y逐步下降.
该函数的对称轴是x=13,所以,当 时,学生的接受能力逐步增强;当 时,学生的接受能力逐步降低.
(2)第10min时,学生的接受能力是多少?
解:当x=10时,
y=-0.1×102+2.6×10+43
=59
即当x=10min时,学生的接受能力是59.
(3)第几分时,学生的接受能力最强?
解:当x=13时,函数y到达顶点,
即 ymax=-0.1×132+2.6×13+43
=59.9
即当x=13min时,学生的接受能力最强为59.9.
解:(2)用于再投资的资金是16-3=13(万元),经分析,有两种投资方式符合要求.一种是取A,B,E各一股,投入资金为5+2+6=13(万元),收益为0.55+0.4+0.9=1.85(万元)>1.6(万元);另一种是取B,D,E各一股,投入资金为2+4+6=12(万元)<13(万元),收益为0.4+0.5+0.9=1.8(万元)>(万元).
某饮料经营部每天的固定成本为200元,其销售的饮料每瓶进价为5元.销售单价与日均销售量的关系如下:
①若记销售单价比每瓶进价多X元,日均毛利润(毛利润=售价-进价-固定成本)为y元,求Y 关于X的函数解析式和自变量的取值范围;
②若要使日均毛利润达到最大,销售单价应定为多少元(精确到0.1元)?最大日均毛利润为多少元?
销售单价(元)
6
7
8
9
10
11
12
日均销售量(瓶)
480
440
400
360
320
280
240
一个球从地面上竖直向上弹起时的速度为10m/s,经过t(s)时球的高度为h(m).已知物体竖直上抛运动中,h=v0t- ? gt?(v0表示物体运动上弹开始时的速度,g表示重力系数,取g=10m/s?).问球从弹起至回到地面需要多少时间?经多少时间球的高度达到3.75m?
地面
1
2
0
-1
-2
t(s)
1
2
3
4
5
6
h(m)
地面
1
2
0
-1
-2
t(s)
1
2
3
4
5
6
h(m)
解:
由题意,得h关于t的二次函数
解析式为h=10t-5t?
取h=0,得一元二次方程
10t-5t?=0
解方程得t1=0;t2=2
球从弹起至回到地面需要时间为t2-t1=2(s)
取h=3.75,得一元二次方程10t-5t?=3.75
解方程得t1=0.5;t2=1.5
答:球从弹起至回到地面需要时间为2(s);
经过圆心的0.5s或1.5s球的高度达到3.75m
1、一球从地面抛出的运动路线呈抛物线,如图,
当球离抛出地的水平距离为 30m 时,达到最
大高10m
⑴ 求球运动路线的函数解析式和自变量的取值范围;
⑵ 求球被抛出多远;
⑶ 当球的高度为5m时,球离抛出地面的水平距离
是多少m?
40
50
30
20
10
x
5
10
15
y
反过来,也可利用二次函数的图象
求一元二次方程的解
二次函数y=ax?+bx+c
归纳小结:
y=0
一元二次方程ax?+bx+c=0
两根为x1=m;x2=n
则
函数与x轴交点坐标为:
(m,0);(n,0)
用总长度为24m的不锈钢材料制成如图30-4-6所示的外观为矩形的框架,其横档和竖档分别与AD,AB平行.设AB=xm,当x为多少时,矩形框架
ABCD的面积S最大?最大面积是多少平方米?
解:∵
∴当x=3时,S有最大值,且S最大=12m2.
答:当x=3时,矩形框架ABCD的面积最大,最大面积为12m2.
如图,B船位于A船正东26km处,现在A,B两船同时出发,A船以12km/h的速度朝正北方向行驶,B船以5km/h的速度朝正西方向行驶,何时两船相距最近?最近距离是多少?
A’
A
B’
B
①设经过t时后,A、B两船分别到达A/、B/(如图),则两船的距离S应为多少 ?
②如何求出S的最小值?
A’
A
B’
B
如图,B船位于A船正东26km处,现在A,B两船同时出发,A船以12km/h的速度朝正北方向行驶,B船以5km/h的速度朝正西方向行驶,何时两船相距最近?最近距离是多少?
合作探究
A
B
C
D
a
如图,有长为24米的篱笆,围成中间隔有一道篱笆的长方形的花圃,且花圃的长可借用一段墙体(墙体的最大可用长度10米):
(1)如果所围成的花圃的面积为45平方米,试求宽AB的值;
(2)按题目的设计要求,能围成面积比45平方米更大吗?
变式:如图,在一面靠墙的空地上用长为24米的篱笆,围成中间隔有二道篱笆的长方形花圃,设花圃的宽AB为x米,面积为S平方米.
(1)求S与x的函数关系式及自变量的取值范围;
(2)当x取何值时所围成的花圃面积最大,最大值是多少?
(3)若墙的最大可用长度为8米,则求围成花圃的最大面积.
A
B
C
D
用二次函数的知识解决图形面积等问题的一般步骤:
把实际问题转化为数学问题
二次函数
问题求解
找出实际问题的答案
及
时
总
结
谢谢聆听
(第2课时)
第5章 二次函数
2020-2021学年度苏科版九年级下册
二次函数的图象与x轴有没有交点,由什么决定?
复习思考
由b?-4ac的符号决定
b?-4ac﹥0,有两个交点
b?-4ac=0,只有一个交点
b?-4ac﹤0,没有交点
求出二次函数y=10x-5x?图象的顶点坐标,与x轴的交点坐标,并画出函数的大致图象
启明公司生产某种产品,每件产品成本是3元,售价是4元,年销售量是10万件,为了获得更好的效益,公司准备拿出一定的资金做广告,根据经验,每年投入的广告费是x(万元)时,产品的年销售量将是原销售量的y倍,且y=﹣ x2+ x+ ,如果把利润看作是销售总额减去成本费和广告费:
⑴试写出年利润s(万元)与广告费x(万元)的函数关系式,并计算广告费是多少万元时,公司获得的年利润最大及最大年利润是多少万元.
解:⑴S=10×( )×(4-3)-x=-x2+6x+7
当x= =3时,
S最大= = = =16
∴当广告费是3万元时,公司获得的最大年利益是16万元.
⑵把①中的最大利润留出3万元做广告,其余资金投资新项目,现有六个项目可供选择,各项目每股投资金额和预计年收益如下表:
项目
A
B
C
D
E
F
每股(万元)
5
2
6
4
6
8
收益(万元)
0.55
0.4
0.6
0.5
0.9
1
如果每个项目只能投一股,且要求所有投资项目的收益总额不低于1.6万元,问有几种符合要求的投资方式.写出每种投资方式所选的项目.
心理学家发现,通常情况下,学生对知识的接受能力y与学习知识所用的连续时间xmin之间满足函数关系
,
y的值越大,表示接受能力越强.
(1)x在什么范围内,学生的接受能力逐步增强?x又在什么范围内,学生的接受能力逐步降低?
解:观察函数关系式可知该函数是一条开口向下的抛物线,所以当x在对称轴左侧时,y逐步递增,当x在对称轴右侧时,y逐步下降.
该函数的对称轴是x=13,所以,当 时,学生的接受能力逐步增强;当 时,学生的接受能力逐步降低.
(2)第10min时,学生的接受能力是多少?
解:当x=10时,
y=-0.1×102+2.6×10+43
=59
即当x=10min时,学生的接受能力是59.
(3)第几分时,学生的接受能力最强?
解:当x=13时,函数y到达顶点,
即 ymax=-0.1×132+2.6×13+43
=59.9
即当x=13min时,学生的接受能力最强为59.9.
解:(2)用于再投资的资金是16-3=13(万元),经分析,有两种投资方式符合要求.一种是取A,B,E各一股,投入资金为5+2+6=13(万元),收益为0.55+0.4+0.9=1.85(万元)>1.6(万元);另一种是取B,D,E各一股,投入资金为2+4+6=12(万元)<13(万元),收益为0.4+0.5+0.9=1.8(万元)>(万元).
某饮料经营部每天的固定成本为200元,其销售的饮料每瓶进价为5元.销售单价与日均销售量的关系如下:
①若记销售单价比每瓶进价多X元,日均毛利润(毛利润=售价-进价-固定成本)为y元,求Y 关于X的函数解析式和自变量的取值范围;
②若要使日均毛利润达到最大,销售单价应定为多少元(精确到0.1元)?最大日均毛利润为多少元?
销售单价(元)
6
7
8
9
10
11
12
日均销售量(瓶)
480
440
400
360
320
280
240
一个球从地面上竖直向上弹起时的速度为10m/s,经过t(s)时球的高度为h(m).已知物体竖直上抛运动中,h=v0t- ? gt?(v0表示物体运动上弹开始时的速度,g表示重力系数,取g=10m/s?).问球从弹起至回到地面需要多少时间?经多少时间球的高度达到3.75m?
地面
1
2
0
-1
-2
t(s)
1
2
3
4
5
6
h(m)
地面
1
2
0
-1
-2
t(s)
1
2
3
4
5
6
h(m)
解:
由题意,得h关于t的二次函数
解析式为h=10t-5t?
取h=0,得一元二次方程
10t-5t?=0
解方程得t1=0;t2=2
球从弹起至回到地面需要时间为t2-t1=2(s)
取h=3.75,得一元二次方程10t-5t?=3.75
解方程得t1=0.5;t2=1.5
答:球从弹起至回到地面需要时间为2(s);
经过圆心的0.5s或1.5s球的高度达到3.75m
1、一球从地面抛出的运动路线呈抛物线,如图,
当球离抛出地的水平距离为 30m 时,达到最
大高10m
⑴ 求球运动路线的函数解析式和自变量的取值范围;
⑵ 求球被抛出多远;
⑶ 当球的高度为5m时,球离抛出地面的水平距离
是多少m?
40
50
30
20
10
x
5
10
15
y
反过来,也可利用二次函数的图象
求一元二次方程的解
二次函数y=ax?+bx+c
归纳小结:
y=0
一元二次方程ax?+bx+c=0
两根为x1=m;x2=n
则
函数与x轴交点坐标为:
(m,0);(n,0)
用总长度为24m的不锈钢材料制成如图30-4-6所示的外观为矩形的框架,其横档和竖档分别与AD,AB平行.设AB=xm,当x为多少时,矩形框架
ABCD的面积S最大?最大面积是多少平方米?
解:∵
∴当x=3时,S有最大值,且S最大=12m2.
答:当x=3时,矩形框架ABCD的面积最大,最大面积为12m2.
如图,B船位于A船正东26km处,现在A,B两船同时出发,A船以12km/h的速度朝正北方向行驶,B船以5km/h的速度朝正西方向行驶,何时两船相距最近?最近距离是多少?
A’
A
B’
B
①设经过t时后,A、B两船分别到达A/、B/(如图),则两船的距离S应为多少 ?
②如何求出S的最小值?
A’
A
B’
B
如图,B船位于A船正东26km处,现在A,B两船同时出发,A船以12km/h的速度朝正北方向行驶,B船以5km/h的速度朝正西方向行驶,何时两船相距最近?最近距离是多少?
合作探究
A
B
C
D
a
如图,有长为24米的篱笆,围成中间隔有一道篱笆的长方形的花圃,且花圃的长可借用一段墙体(墙体的最大可用长度10米):
(1)如果所围成的花圃的面积为45平方米,试求宽AB的值;
(2)按题目的设计要求,能围成面积比45平方米更大吗?
变式:如图,在一面靠墙的空地上用长为24米的篱笆,围成中间隔有二道篱笆的长方形花圃,设花圃的宽AB为x米,面积为S平方米.
(1)求S与x的函数关系式及自变量的取值范围;
(2)当x取何值时所围成的花圃面积最大,最大值是多少?
(3)若墙的最大可用长度为8米,则求围成花圃的最大面积.
A
B
C
D
用二次函数的知识解决图形面积等问题的一般步骤:
把实际问题转化为数学问题
二次函数
问题求解
找出实际问题的答案
及
时
总
结
谢谢聆听
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
