2012【优化方案】精品课件:物理教科必修1第2章第六节
文档属性
| 名称 | 2012【优化方案】精品课件:物理教科必修1第2章第六节 |

|
|
| 格式 | rar | ||
| 文件大小 | 885.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2011-12-20 00:00:00 | ||
图片预览









文档简介
(共47张PPT)
第六节 力的分解
课标定位:
应用:1. 用作图法解决有关力的分解问题.
2.用力的分解分析生活和生产中的有关问题.
理解:1. 力的分解的方法.
2.力的正交分解.
认识:1. 力的分解的概念.
2.力的分解是力的合成的逆运算.
第六节
核心要点突破
课堂互动讲练
知能优化训练
课前自主学案
课标定位
课前自主学案
一、一个力可以用几个力来替代
一个力的作用可以用几个力的共同作用来等效替代,这几个力称为那一个力的_______.求一个已知力的分力叫做力的________.
二、力的分解方法
1.力的分解遵循的法则:力的分解是力的合成的________,同样遵循_______________定则.
分力
分解
逆运算
平行四边形
2.力的分解的原则
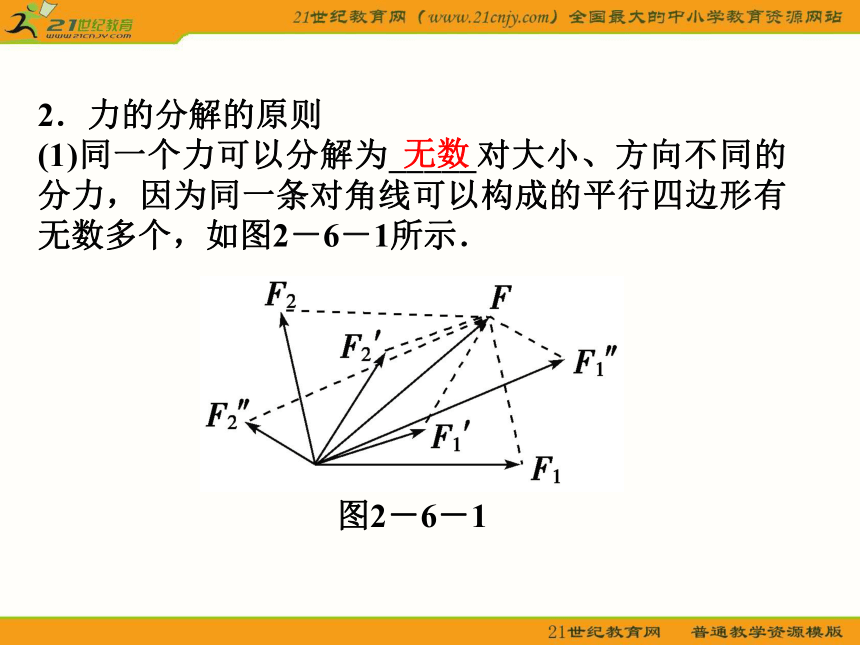
(1)同一个力可以分解为_____对大小、方向不同的分力,因为同一条对角线可以构成的平行四边形有无数多个,如图2-6-1所示.
图2-6-1
无数
(2)在实际问题中要根据力的_____________进行分解.
三、力的正交分解
将力沿着____________的方向分解的方法.
作用效果
相互垂直
核心要点突破
一、力的分解方法(一)——按效果分解
1.根据一条对角线可以作出无数个平行四边形,即有无数组解,但在实际分解时,一般要按力的实际作用效果分解,其方法是:
(1)先根据力的实际效果确定两个分力的方向;
(2)再根据两个分力的方向作出力的平行四边形;
(3)解三角形或解平行四边形,计算出分力的大小和方向.
2.按实际效果分解的几个实例
实 例 分 析
地面上物体受斜向上的拉力F,拉力F一方面使物体沿水平地面前进,另一方面向上提物体,因此拉力F可分解为水平向前的力F1和竖直向上的力F2
质量为m的物体静止在斜面上,其重力产生两个效果:一是使物体具有沿斜面下滑趋势的分力F1;二是使物体压紧斜面的分力F2.F1=mgsinα,F2=mgcosα
即时应用(即时突破,小试牛刀)
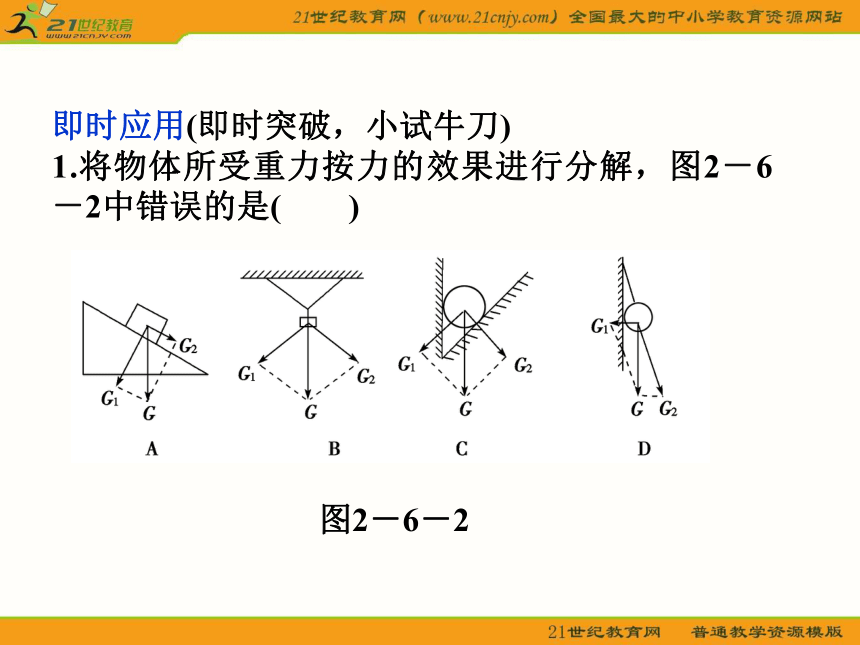
1.将物体所受重力按力的效果进行分解,图2-6-2中错误的是( )
图2-6-2
解析:选C.A项中物体重力分解为垂直于斜面使物体压紧斜面的分力G1和沿斜面向下使物体向下滑的分力G2;B项中物体的重力分解为沿两条细绳使细绳张紧的分力G1和G2,A、B项图画得正确.C项中物体的重力应分解为垂直于两接触面使物体紧压两接触面的分力G1和G2,故C项图画错.D项中物体的重力分解为水平向左压紧墙的分力G1和沿绳向下使绳张紧的分力G2,故D项图画得正确.
二、力的分解方法(二)——正交分解法
1.目的:将力的合成化简为同向、反向或垂直方向的分力,便于运用普通代数运算公式解决矢量的运算,“分”的目的是为了更好的“合”.
2.适用情况:适用于计算三个或三个以上力的合成.
3.步骤
(1)建立坐标系:以共点力的作用点为坐标原点,直角坐标系x轴和y轴的选择应使尽量多的力在坐标轴上.
(2)正交分解各力:将每一个不在坐标轴上的力分解到x轴和y轴上,并在图上注明,用符号Fx和Fy表示,如图2-6-3所示.
图2-6-3
特别提醒:(1)建立坐标系之前,要对物体进行受力分析,画出各力的示意图,一般各力的作用点都移到物体的重心上.
(2)建立坐标系的原则:使尽量多的力落在坐标轴上,尽量减少分解力的个数.
三、对力的分解的讨论
力分解时有解或无解,简单地说就是代表合力的对角线与给定的代表分力的有向线段是否能构成平行四边形(或三角形).若可以构成平行四边形
(或三角形),说明该合力可以分解成给定的分力,即有解.如果不能构成平行四边形(或三角形),说明该合力不能按给定的分力分解,即无解.具体情况有以下几种:
已知条件 示意图 解的情况
已知合力和两个分力的方向
已知合力和两个分力的大小
已知条件 示意图 解的情况
已知合力和一个分力的大小和方向
已知合力和一个分力的大小和另一个分力的方向 有三种情况:(图略)
(1)当F1=Fsinθ或F1≥F时,有一组解.
(2)当F1(3)当Fsinθ特别提醒:可以将关于力的分解是有解还是无解,以及有几个解的问题转化为能否作出力的平行四边形(或三角形)或能作几个平行四边形(或三角形)的问题.
即时应用(即时突破,小试牛刀)
2.一个已知力F=10 N,把F分解为F1和F2两个分力,已知分力F1与F夹角为30°,则F2的大小
( )
A.一定小于10 N B.可能等于10 N
C.可能大于10 N D.最小等于5 N
解析:选BCD.对力F进行分解.画出平行四边形,由图可知当F2垂直于F1时F2最小,最小值为F2=Fsin30°=5 N,故B、C、D正确.
例1
如图2-6-4所示,一位重600 N的演员悬挂在绳上.若AO绳与水平方向的夹角为37°,BO绳水平,则AO、BO两绳受到的力各为多大?(sin37°=0.6,cos37°=0.8)
课堂互动讲练
按力的实际作用效果分解力
图2-6-4
【思路点拨】 可根据人的拉力对O点的作用效果进行分解,作出力的平行四边形,然后利用几何关系进行求解.
【精讲精析】 人对竖直绳的拉力F等于人的重力G,由于该力的作用AO、BO也受到拉力的作用,因此F产生了沿AO方向、BO方向使O点拉绳的分力F1、F2,将F沿AO方向和BO方向分解成两个分力.如图2-6-5所示,由画出的平行四边形可知:
图2-6-5
【答案】 1000 N 800 N
【方法总结】 (1)确定力的实际作用效果是正确进行力的分解的前提,力的作用效果的确定:一方面靠自己观察感受,另一方面靠分析推理.
(2)分解力时要注意合力与分力必须作用在同一物体上.
变式训练1 如图2-6-6所示,重为G的物体放在倾角为α的光滑斜面上,分别被垂直斜面的挡板如甲图和竖直放置的挡板如乙图挡住.试对两个图中物体的重力根据力的作用效果进行分解,作出示意图,并求出两分力的大小.
图2-6-6
解析:分解示意图如下图所示.
甲图中两分力大小分别为:
G1=Gsinα,G2=Gcosα.
乙图中两分力大小分别为:
G1′=Gtanα,G2′=G/cosα.
答案:见解析
例2
正交分解法的应用
用轻弹簧竖直悬挂质量为m的物体,静止时弹簧伸长量为L.现用该弹簧沿斜面方向拉住质量为2m的物体,系统静止时弹簧伸长量也为L.斜面倾角为30°,如图2-6-7所示.则物体所受摩擦力( )
图2-6-7
【思路点拨】 (1)先由二力平衡分析弹簧弹力;(2)在斜面上物体受力很多,用正交分解法;(3)胡克定律的应用.
【精讲精析】 弹簧竖直悬挂时,如图2-6-8甲所示,有
F-mg=0①
F=kL②
图2-6-8
系统在斜面上静止时,如图乙所示,有
沿斜面F′+f-2mgsin30°=0③
F′=kL④
由①②③④可解得f=0.
【答案】 A
【方法总结】 物体受多个力作用时,可选择正交分解法,先“分”,再“合”来处理.
变式训练2 一个物体A的重力为G,放在粗糙的水平面上,物体与水平面间的动摩擦因数为μ,如图2-6-9所示,拉力与水平方向的夹角为θ,为拉动此物体做匀速直线运动,求拉力F为多大?
图2-6-9
解析:首先分析物体A,A受到四个力作用,分别为:拉力F、重力G,支持力N,摩擦力f,如图:
例3
如图2-6-10所示,半圆形支架BAD,两细绳OA和OB结于圆心O,下悬重为G的物体,使OA绳固定不动,将OB绳的B端沿半圆支架从水平位置逐渐移至竖直位置C的过程中,分析OA绳和OB绳所受的力大小如何变化?
力的动态分析
图2-6-10
【思路点拨】 本题可利用图解法来求,根据题意画好矢量图,合力一定,一个力方向变化时,对另一个分力的影响,从图上可清楚的表示出来.
【自主解答】因为绳结点O受重物的拉力T,所以才使OA绳和OB绳受力,因此将拉力T分解为TA、TB(如图2-6-11所示).OA绳固定,则TA的方向不变,在OB向上靠近OC的过程中,在B1、B2、B3三个位置,两绳受的力分别为TA1和TB1、TA2和TB2、TA3和TB3.从图形上看出,TA逐渐变小,而TB却是先变小后增大,当OB和OA垂直时,TB最小.
图2-6-11
【答案】 OA绳拉力逐渐变小,OB绳拉力先变小后变大
【方法总结】 在这类动态分析题中,合力是一个恒力(即大小、方向都不变),其中一个分力F1方向是一定的,另一个分力F2大小、方向都在变,当F2与F1垂直时,F2取得最小值,解题时要注意这一特点.
变式训练3 如图2-6-12所示,小球放在光滑的墙与装有铰链的光滑薄板之间,当墙与薄板之间的夹角θ缓慢地增大到90°的过程中( )
图2-6-12
A.小球对薄板的正压力增大
B.小球对墙的正压力减小
C.小球对墙的压力先减小,后增大
D.小球对木板的压力不可能小于球的重力
解析:选BD.根据小球重力的作用效果,可以将重力G分解为使球压板的力F1和使球压墙的力F2,作出平行四边形如图所示,当θ增大时如图中虚线所示,F1、F2均变小,而且在θ=90°时,F1变为最小值,等于G,所以B、D均正确.
知能优化训练
本部分内容讲解结束
点此进入课件目录
按ESC键退出全屏播放
谢谢使用
第六节 力的分解
课标定位:
应用:1. 用作图法解决有关力的分解问题.
2.用力的分解分析生活和生产中的有关问题.
理解:1. 力的分解的方法.
2.力的正交分解.
认识:1. 力的分解的概念.
2.力的分解是力的合成的逆运算.
第六节
核心要点突破
课堂互动讲练
知能优化训练
课前自主学案
课标定位
课前自主学案
一、一个力可以用几个力来替代
一个力的作用可以用几个力的共同作用来等效替代,这几个力称为那一个力的_______.求一个已知力的分力叫做力的________.
二、力的分解方法
1.力的分解遵循的法则:力的分解是力的合成的________,同样遵循_______________定则.
分力
分解
逆运算
平行四边形
2.力的分解的原则
(1)同一个力可以分解为_____对大小、方向不同的分力,因为同一条对角线可以构成的平行四边形有无数多个,如图2-6-1所示.
图2-6-1
无数
(2)在实际问题中要根据力的_____________进行分解.
三、力的正交分解
将力沿着____________的方向分解的方法.
作用效果
相互垂直
核心要点突破
一、力的分解方法(一)——按效果分解
1.根据一条对角线可以作出无数个平行四边形,即有无数组解,但在实际分解时,一般要按力的实际作用效果分解,其方法是:
(1)先根据力的实际效果确定两个分力的方向;
(2)再根据两个分力的方向作出力的平行四边形;
(3)解三角形或解平行四边形,计算出分力的大小和方向.
2.按实际效果分解的几个实例
实 例 分 析
地面上物体受斜向上的拉力F,拉力F一方面使物体沿水平地面前进,另一方面向上提物体,因此拉力F可分解为水平向前的力F1和竖直向上的力F2
质量为m的物体静止在斜面上,其重力产生两个效果:一是使物体具有沿斜面下滑趋势的分力F1;二是使物体压紧斜面的分力F2.F1=mgsinα,F2=mgcosα
即时应用(即时突破,小试牛刀)
1.将物体所受重力按力的效果进行分解,图2-6-2中错误的是( )
图2-6-2
解析:选C.A项中物体重力分解为垂直于斜面使物体压紧斜面的分力G1和沿斜面向下使物体向下滑的分力G2;B项中物体的重力分解为沿两条细绳使细绳张紧的分力G1和G2,A、B项图画得正确.C项中物体的重力应分解为垂直于两接触面使物体紧压两接触面的分力G1和G2,故C项图画错.D项中物体的重力分解为水平向左压紧墙的分力G1和沿绳向下使绳张紧的分力G2,故D项图画得正确.
二、力的分解方法(二)——正交分解法
1.目的:将力的合成化简为同向、反向或垂直方向的分力,便于运用普通代数运算公式解决矢量的运算,“分”的目的是为了更好的“合”.
2.适用情况:适用于计算三个或三个以上力的合成.
3.步骤
(1)建立坐标系:以共点力的作用点为坐标原点,直角坐标系x轴和y轴的选择应使尽量多的力在坐标轴上.
(2)正交分解各力:将每一个不在坐标轴上的力分解到x轴和y轴上,并在图上注明,用符号Fx和Fy表示,如图2-6-3所示.
图2-6-3
特别提醒:(1)建立坐标系之前,要对物体进行受力分析,画出各力的示意图,一般各力的作用点都移到物体的重心上.
(2)建立坐标系的原则:使尽量多的力落在坐标轴上,尽量减少分解力的个数.
三、对力的分解的讨论
力分解时有解或无解,简单地说就是代表合力的对角线与给定的代表分力的有向线段是否能构成平行四边形(或三角形).若可以构成平行四边形
(或三角形),说明该合力可以分解成给定的分力,即有解.如果不能构成平行四边形(或三角形),说明该合力不能按给定的分力分解,即无解.具体情况有以下几种:
已知条件 示意图 解的情况
已知合力和两个分力的方向
已知合力和两个分力的大小
已知条件 示意图 解的情况
已知合力和一个分力的大小和方向
已知合力和一个分力的大小和另一个分力的方向 有三种情况:(图略)
(1)当F1=Fsinθ或F1≥F时,有一组解.
(2)当F1
即时应用(即时突破,小试牛刀)
2.一个已知力F=10 N,把F分解为F1和F2两个分力,已知分力F1与F夹角为30°,则F2的大小
( )
A.一定小于10 N B.可能等于10 N
C.可能大于10 N D.最小等于5 N
解析:选BCD.对力F进行分解.画出平行四边形,由图可知当F2垂直于F1时F2最小,最小值为F2=Fsin30°=5 N,故B、C、D正确.
例1
如图2-6-4所示,一位重600 N的演员悬挂在绳上.若AO绳与水平方向的夹角为37°,BO绳水平,则AO、BO两绳受到的力各为多大?(sin37°=0.6,cos37°=0.8)
课堂互动讲练
按力的实际作用效果分解力
图2-6-4
【思路点拨】 可根据人的拉力对O点的作用效果进行分解,作出力的平行四边形,然后利用几何关系进行求解.
【精讲精析】 人对竖直绳的拉力F等于人的重力G,由于该力的作用AO、BO也受到拉力的作用,因此F产生了沿AO方向、BO方向使O点拉绳的分力F1、F2,将F沿AO方向和BO方向分解成两个分力.如图2-6-5所示,由画出的平行四边形可知:
图2-6-5
【答案】 1000 N 800 N
【方法总结】 (1)确定力的实际作用效果是正确进行力的分解的前提,力的作用效果的确定:一方面靠自己观察感受,另一方面靠分析推理.
(2)分解力时要注意合力与分力必须作用在同一物体上.
变式训练1 如图2-6-6所示,重为G的物体放在倾角为α的光滑斜面上,分别被垂直斜面的挡板如甲图和竖直放置的挡板如乙图挡住.试对两个图中物体的重力根据力的作用效果进行分解,作出示意图,并求出两分力的大小.
图2-6-6
解析:分解示意图如下图所示.
甲图中两分力大小分别为:
G1=Gsinα,G2=Gcosα.
乙图中两分力大小分别为:
G1′=Gtanα,G2′=G/cosα.
答案:见解析
例2
正交分解法的应用
用轻弹簧竖直悬挂质量为m的物体,静止时弹簧伸长量为L.现用该弹簧沿斜面方向拉住质量为2m的物体,系统静止时弹簧伸长量也为L.斜面倾角为30°,如图2-6-7所示.则物体所受摩擦力( )
图2-6-7
【思路点拨】 (1)先由二力平衡分析弹簧弹力;(2)在斜面上物体受力很多,用正交分解法;(3)胡克定律的应用.
【精讲精析】 弹簧竖直悬挂时,如图2-6-8甲所示,有
F-mg=0①
F=kL②
图2-6-8
系统在斜面上静止时,如图乙所示,有
沿斜面F′+f-2mgsin30°=0③
F′=kL④
由①②③④可解得f=0.
【答案】 A
【方法总结】 物体受多个力作用时,可选择正交分解法,先“分”,再“合”来处理.
变式训练2 一个物体A的重力为G,放在粗糙的水平面上,物体与水平面间的动摩擦因数为μ,如图2-6-9所示,拉力与水平方向的夹角为θ,为拉动此物体做匀速直线运动,求拉力F为多大?
图2-6-9
解析:首先分析物体A,A受到四个力作用,分别为:拉力F、重力G,支持力N,摩擦力f,如图:
例3
如图2-6-10所示,半圆形支架BAD,两细绳OA和OB结于圆心O,下悬重为G的物体,使OA绳固定不动,将OB绳的B端沿半圆支架从水平位置逐渐移至竖直位置C的过程中,分析OA绳和OB绳所受的力大小如何变化?
力的动态分析
图2-6-10
【思路点拨】 本题可利用图解法来求,根据题意画好矢量图,合力一定,一个力方向变化时,对另一个分力的影响,从图上可清楚的表示出来.
【自主解答】因为绳结点O受重物的拉力T,所以才使OA绳和OB绳受力,因此将拉力T分解为TA、TB(如图2-6-11所示).OA绳固定,则TA的方向不变,在OB向上靠近OC的过程中,在B1、B2、B3三个位置,两绳受的力分别为TA1和TB1、TA2和TB2、TA3和TB3.从图形上看出,TA逐渐变小,而TB却是先变小后增大,当OB和OA垂直时,TB最小.
图2-6-11
【答案】 OA绳拉力逐渐变小,OB绳拉力先变小后变大
【方法总结】 在这类动态分析题中,合力是一个恒力(即大小、方向都不变),其中一个分力F1方向是一定的,另一个分力F2大小、方向都在变,当F2与F1垂直时,F2取得最小值,解题时要注意这一特点.
变式训练3 如图2-6-12所示,小球放在光滑的墙与装有铰链的光滑薄板之间,当墙与薄板之间的夹角θ缓慢地增大到90°的过程中( )
图2-6-12
A.小球对薄板的正压力增大
B.小球对墙的正压力减小
C.小球对墙的压力先减小,后增大
D.小球对木板的压力不可能小于球的重力
解析:选BD.根据小球重力的作用效果,可以将重力G分解为使球压板的力F1和使球压墙的力F2,作出平行四边形如图所示,当θ增大时如图中虚线所示,F1、F2均变小,而且在θ=90°时,F1变为最小值,等于G,所以B、D均正确.
知能优化训练
本部分内容讲解结束
点此进入课件目录
按ESC键退出全屏播放
谢谢使用
同课章节目录
- 第一章 运动的描述
- 1 质点 参考系 空间 时间
- 2 位置变化的描述——位移
- 3 运动快慢与方向的描述——速度
- 4 速度变化快慢的描述——加速度
- 5 匀变速直线运动速度与时间的关系
- 6 匀变速直线运动位移与时间的关系
- 7 对自由落体运动的研究
- 8 匀变速直线运动规律的应用
- 9 测定匀变速直线运动的加速度
- 第二章 力
- 1 力
- 2 重力
- 3 弹力
- 4 摩擦力
- 5 力的合成
- 6 力的分解
- 第三章 牛顿运动定律
- 1 牛顿第一定律
- 2 探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 牛顿第三定律
- 5 牛顿运动定律的应用
- 6 超重与失重
- 第四章 物体的平衡
- 1 共点力作用下物体的平衡
- 2 共点力平衡条件的应用
- 3 平衡的稳定性(选学)
