2012【优化方案】精品课件:物理教科必修1第2章第五节
文档属性
| 名称 | 2012【优化方案】精品课件:物理教科必修1第2章第五节 |

|
|
| 格式 | rar | ||
| 文件大小 | 648.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2011-12-20 00:00:00 | ||
图片预览









文档简介
(共41张PPT)
第五节 力的合成
课标定位:
应用:1. 运用力的平行四边形定则求共点力的合力.
2.分析生产和生活中的有关问题.
理解:1. 力的平行四边形定则.
2.合力的大小和分力夹角的关系.
认识:1. 合力、分力、力的合成以及共点力的概念.
2.力的平行四边形定则只适用于共点力.
第五节
核心要点突破
课堂互动讲练
知能优化训练
课前自主学案
课标定位
课前自主学案
一、力的合成
1.合力与分力:如果一个力的___________与几个力共同作用的_______相同,这个力就叫做那几个力的______,原来的几个力叫做这个力的________.
2.力的合成:求几个力的______叫做力的合成.
3.共点力:作用于物体上同一点,或者力的作用线相交于同一点的几个力称为共点力.
作用效果
效果
合力
分力
合力
二、实验:探究共点力合成的规律
1.实验目的:探究合力与分力的关系.
2.实验原理:根据等效替代法,将橡皮条的一端固定,另一端用两个力F1、F2拉,使其伸长一定长度,再用一个力F作用于橡皮条的同一点,使其伸长同样的长度,那么F与F1、F2的作用效果相同;若记下F1、F2的大小和方向,画出各个力的图示,就可以研究F与F1、F2的关系了.
3.实验器材:白纸、木板、橡皮筋、细绳、刻度尺、弹簧测力计、铅笔、滑轮(若干)、图钉(若干).
4.实验步骤
(1)在水平放置的图板上固定一张白纸,将橡皮筋的一端固定在图板上的K点处,橡皮筋的自然长度为KE,如图2-5-1甲所示.
(2)让橡皮筋在互为120°的两个弹簧测力计的共同作用下沿KE方向由E点伸长至O点,此时弹簧测力计的示数分别为F1和F2,做出F1和F2的图示,如图乙所示.撤去F1和F2,用一个弹簧测力计直接拉着橡皮筋沿KE伸长到O点,此时弹簧测力计的示数为F,如图丙所示,在同一张纸上作出F的图示.
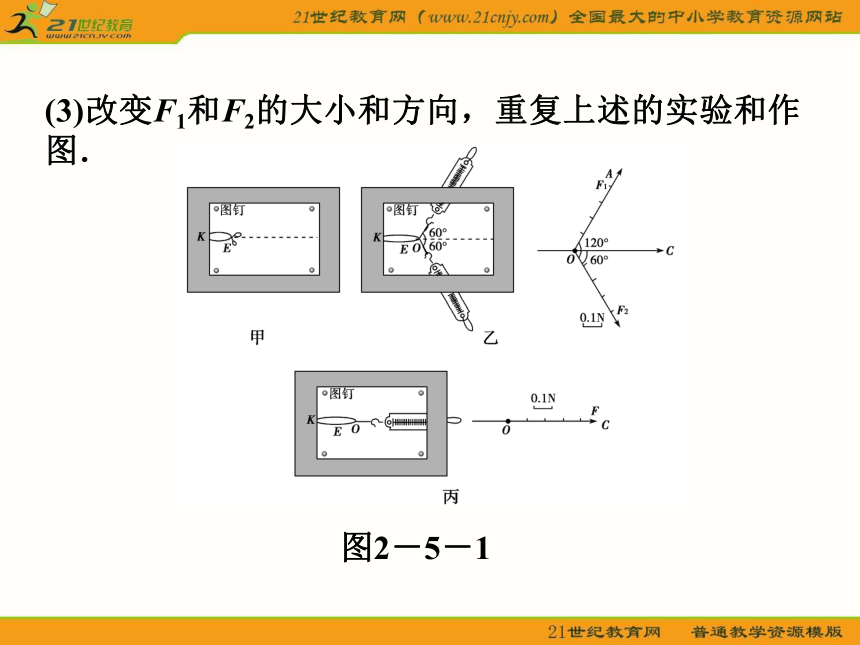
(3)改变F1和F2的大小和方向,重复上述的实验和作图.
图2-5-1
5.实验结论:用表示共点力F1和F2的线段为邻边作平行四边形,那么合力F的大小和方向就可以用这两个邻边之间的对角线表示.这就是力的平行四边形定则.
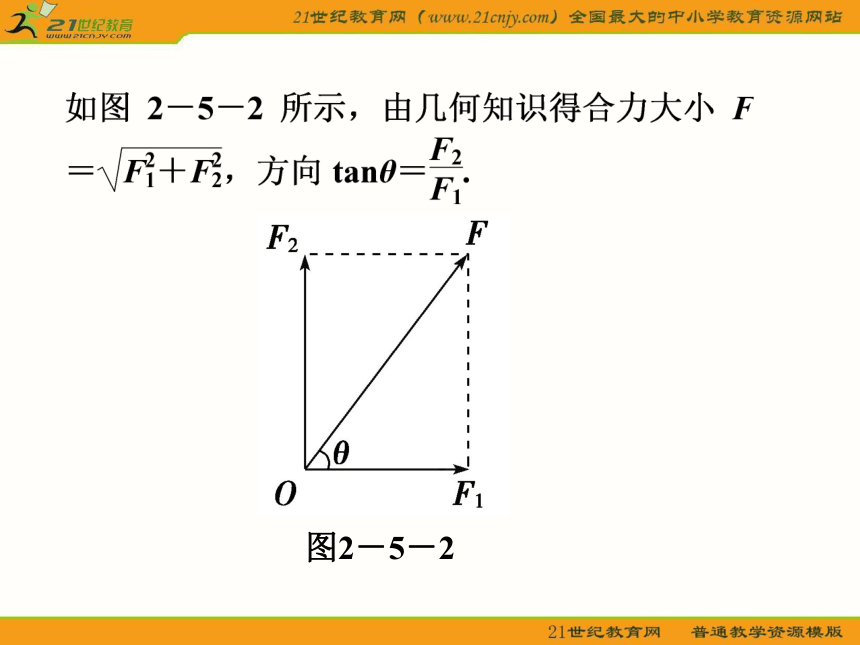
三、互成直角的两个力的合成
1.互成直角的共点力的合成
图2-5-2
2.求多个共点力合成的方法
先把任意两个力合成,求得合力后,再把这个合力与___________合成,依次进行,最终求得全部共点力的合力.
第三个力
思考感悟
两个人共提一桶水,要想省力,两个人拉力间的夹角应大些还是小些,为什么?请用橡皮筋做个简单实验来验证你的结论.
提示:夹角应小一些.两个力的大小确定时,合力随这两个力之间夹角的减小而增大.反之,保证合力不变时(在这个问题中,合力的大小等于一桶水重力的大小),两分力的大小会随两个力间夹角的减小而减小,因此,夹角小一些,会更省力.
核心要点突破
一、合力与分力的关系
1.正确理解合力与分力
(1)合力与几个分力间是相互替代关系,受力分析时,分力与合力不能同时作为物体所受的力.
(2)只有同一物体同时受到的力才能合成.
2.合力与分力间的大小关系
(1)两力同向时合力最大:F=F1+F2,方向与两力同向.
(2)两力方向相反时,合力最小:F=|F1-F2|,方向与两力中较大的力同向.
(3)两力成某一角度θ时,如图2-5-3所示,三角形AOC的每一条边对应一个力,由几何知识可知:两边之和大于第三边,两边之差小于第三边,即|F1-F2|图2-5-3
(4)夹角θ越大,合力就越小.
(5)合力可以大于等于两分力中的任何一个力,也可以小于等于两分力中的任何一个力.
特别提醒:(1)若三个共点力F1、F2、F3的合力为F,设F1≤F2≤F3.显然,当三个力方向相同时,合力F最大,Fmax=F1+F2+F3.
(2)若三个力中任何一个力在另外两个力的合力的变化范围内,则合力F最小值为零,Fmin=0;若三个力中任何一个力不在另外两个力的合力的变化范围内,则当较小的两个力F1与F2方向相同且与F3方向相反时,合力F最小,Fmin=|F3-(F1+F2)|.
即时应用(即时突破,小试牛刀)
1.关于几个力与其合力,下列说法正确的是( )
A.合力的作用效果跟原来那几个力共同作用产生的效果相同
B.合力与原来那几个力同时作用在物体上
C.合力的作用可以替代原来那几个力的作用
D.求几个力的合力遵循平行四边形定则
解析:选ACD.合力与分力是“等效替代”的关系,即合力的作用效果与几个分力共同作用时的作用效果相同,合力的作用效果可以替代这几个分力的作用效果,不能认为合力与分力同时作用在物体上,所以A、C正确,B不正确;求合力应遵循平行四边形定则,所以D正确.
二、合力的求解方法
1.作图法:要选取统一标度,严格作出力的图示以及平行四边形,用统一标度去度量作出的平行四边形的对角线,求出合力的大小,再量出对角线与某一分力的夹角,求出合力的方向.
2.计算法:设共点力F1、F2的夹角为θ,作出力的合成示意图(如图2-5-4),则F的大小等于OC的长度所对应的力的大小,F的方向与F1成α角.由图可看出,OC是平行四边形OACB的一条对角线,OC又是三角形OAC的一条边.可见,一旦作出了力的合成示意图,就将求解合力的物理问题转化成数学的几何问题了.
图2-5-4
图2-5-5
图2-5-6
特别提醒:(1)作图时,合力、分力要共点,实线、虚线要分清,标度要唯一且适当.
(2)作图法和计算法均为矢量运算的通用方法.
例1
两个共点力的大小分别为F1=15 N,F2=9 N,它们的合力不可能等于( )
A.9 N
B.25 N
C.6 N
D.21 N
课堂互动讲练
合力与分力的关系
【思路点拨】 解答本题时应注意以下三点:
(1)力的合成遵循平行四边形定则.
(2)两分力夹角越小,合力越大.
(3)合力的范围|F1-F2|≤F≤F1+F2.
【精讲精析】 两个力合成时,合力的范围是|F1-F2|≤F合≤F1+F2,即6 N≤F合≤24 N,由此可知,A、C、D可能,B不可能.
【答案】 B
变式训练1 小强的妈妈提一桶水,向上提起的力为150 N,小强和小勇接过来共同来提,关于小强和小勇的用力,下列说法正确的是( )
A.他俩必分别只用75 N的力
B.他俩可分别用100 N的力
C.他俩都可用小于75 N的力
D.他俩的力不可能大于75 N
解析:选B.小强和小勇两人用力的合力大小应为150 N,则两个分力不可能都小于75 N,应该大于等于75 N.
例2
合力的计算
一个物体受到大小相等的两个拉力作用,每个拉力都是100 N,夹角为90°,求这两个力的合力.
【思路点拨】 本题中的两个力大小相等,夹角为90°,所以可以用作图法和计算法来求解合力的大小.
【精讲精析】 法一(作图法):取5 mm长线段表示20 N,作出平行四边形如图2-5-7所示:量得对角线长为35 mm,则合力F大小为140 N,方向沿F1、F2夹角的平分线方向,与F1夹角为45°.
图2-5-7
图2-5-8
【答案】 140 N(或141.4 N) 方向与F1成45°
【方法总结】 (1)在利用作图法求解时,一定要注意各力均使用同一标度.
(2)计算法是根据平行四边形定则作出示意图,把力归结到一个三角形中,然后利用解三角形的方法求出合力(常用方法).
变式训练2 水平横梁一端插在墙壁内,另一端装小滑轮B.一轻绳的一端C固定于墙壁上,另一端跨过滑轮后悬挂一质量m=10 kg的重物,∠CBA=30°,如图2-5-9所示,则滑轮受到绳子的作用力为(g取10 N/kg)( )
图2-5-9
一物体受到同一平面内的三个共点力作用,其大小分别为:F1=30 N,F2=40 N,F3=50 N,则它们的合力的最大值与最小值分别是多少?
【思路点拨】 本题的难点是求合力的最小值,首先要判断出合力的最小值是否为0.
例3
三个力的合成问题
【自主解答】 当三个力方向相同时,其合力最大,最大值为:
Fmax=F1+F2+F3=120 N.
三个力中,较小的两个力是F1和F2,其二者的合力范围F2-F1≤F12≤F1+F2即10 N≤F12≤70 N,包括F3=50 N,所以三个力合力的最小值为零.
【答案】 120 N 0
【方法总结】 三个力合成时,当它们的方向相同时,合力最大,若三个力中较小的两个力的和大于等于第三个力,其差小于第三个力,则三个力的合力的最小值为零,若两个较小力的和小于第三个力,则三个力的合力的最小值等于第三个力减去两个较小力的和,方向与第三个力的方向相同.
变式训练3 物体同时受到同一平面内三个共点力的作用,下列几组力的合力不可能为零的是( )
A.5 N,7 N,8 N
B.5 N,2 N,3 N
C.1 N,5 N,10 N
D.10 N,10 N,10 N
解析:选C.三力合成时,若两个力的合力可与第三力大小相等、方向相反,就可以使这三个力的合力为零,只要第三力在其他两个力合力范围内,其合力就可能为零,即第三力F3要满足:|F1-F2|≤F3≤F1+F2.
A中前两力合力范围为2 N≤F合≤12 N,第三力在其范围内;B中,3 N≤F合≤7 N,第三力在其合力范围内;C中,4 N≤F合≤6 N,第三力不在其合力范围内;D中,0 N≤F合≤20 N,第三力在其合力范围内;故只有C项中,第三力不在前两力合力范围内,C项中的三力合力不可能为零.
知能优化训练
本部分内容讲解结束
点此进入课件目录
按ESC键退出全屏播放
谢谢使用
第五节 力的合成
课标定位:
应用:1. 运用力的平行四边形定则求共点力的合力.
2.分析生产和生活中的有关问题.
理解:1. 力的平行四边形定则.
2.合力的大小和分力夹角的关系.
认识:1. 合力、分力、力的合成以及共点力的概念.
2.力的平行四边形定则只适用于共点力.
第五节
核心要点突破
课堂互动讲练
知能优化训练
课前自主学案
课标定位
课前自主学案
一、力的合成
1.合力与分力:如果一个力的___________与几个力共同作用的_______相同,这个力就叫做那几个力的______,原来的几个力叫做这个力的________.
2.力的合成:求几个力的______叫做力的合成.
3.共点力:作用于物体上同一点,或者力的作用线相交于同一点的几个力称为共点力.
作用效果
效果
合力
分力
合力
二、实验:探究共点力合成的规律
1.实验目的:探究合力与分力的关系.
2.实验原理:根据等效替代法,将橡皮条的一端固定,另一端用两个力F1、F2拉,使其伸长一定长度,再用一个力F作用于橡皮条的同一点,使其伸长同样的长度,那么F与F1、F2的作用效果相同;若记下F1、F2的大小和方向,画出各个力的图示,就可以研究F与F1、F2的关系了.
3.实验器材:白纸、木板、橡皮筋、细绳、刻度尺、弹簧测力计、铅笔、滑轮(若干)、图钉(若干).
4.实验步骤
(1)在水平放置的图板上固定一张白纸,将橡皮筋的一端固定在图板上的K点处,橡皮筋的自然长度为KE,如图2-5-1甲所示.
(2)让橡皮筋在互为120°的两个弹簧测力计的共同作用下沿KE方向由E点伸长至O点,此时弹簧测力计的示数分别为F1和F2,做出F1和F2的图示,如图乙所示.撤去F1和F2,用一个弹簧测力计直接拉着橡皮筋沿KE伸长到O点,此时弹簧测力计的示数为F,如图丙所示,在同一张纸上作出F的图示.
(3)改变F1和F2的大小和方向,重复上述的实验和作图.
图2-5-1
5.实验结论:用表示共点力F1和F2的线段为邻边作平行四边形,那么合力F的大小和方向就可以用这两个邻边之间的对角线表示.这就是力的平行四边形定则.
三、互成直角的两个力的合成
1.互成直角的共点力的合成
图2-5-2
2.求多个共点力合成的方法
先把任意两个力合成,求得合力后,再把这个合力与___________合成,依次进行,最终求得全部共点力的合力.
第三个力
思考感悟
两个人共提一桶水,要想省力,两个人拉力间的夹角应大些还是小些,为什么?请用橡皮筋做个简单实验来验证你的结论.
提示:夹角应小一些.两个力的大小确定时,合力随这两个力之间夹角的减小而增大.反之,保证合力不变时(在这个问题中,合力的大小等于一桶水重力的大小),两分力的大小会随两个力间夹角的减小而减小,因此,夹角小一些,会更省力.
核心要点突破
一、合力与分力的关系
1.正确理解合力与分力
(1)合力与几个分力间是相互替代关系,受力分析时,分力与合力不能同时作为物体所受的力.
(2)只有同一物体同时受到的力才能合成.
2.合力与分力间的大小关系
(1)两力同向时合力最大:F=F1+F2,方向与两力同向.
(2)两力方向相反时,合力最小:F=|F1-F2|,方向与两力中较大的力同向.
(3)两力成某一角度θ时,如图2-5-3所示,三角形AOC的每一条边对应一个力,由几何知识可知:两边之和大于第三边,两边之差小于第三边,即|F1-F2|
(4)夹角θ越大,合力就越小.
(5)合力可以大于等于两分力中的任何一个力,也可以小于等于两分力中的任何一个力.
特别提醒:(1)若三个共点力F1、F2、F3的合力为F,设F1≤F2≤F3.显然,当三个力方向相同时,合力F最大,Fmax=F1+F2+F3.
(2)若三个力中任何一个力在另外两个力的合力的变化范围内,则合力F最小值为零,Fmin=0;若三个力中任何一个力不在另外两个力的合力的变化范围内,则当较小的两个力F1与F2方向相同且与F3方向相反时,合力F最小,Fmin=|F3-(F1+F2)|.
即时应用(即时突破,小试牛刀)
1.关于几个力与其合力,下列说法正确的是( )
A.合力的作用效果跟原来那几个力共同作用产生的效果相同
B.合力与原来那几个力同时作用在物体上
C.合力的作用可以替代原来那几个力的作用
D.求几个力的合力遵循平行四边形定则
解析:选ACD.合力与分力是“等效替代”的关系,即合力的作用效果与几个分力共同作用时的作用效果相同,合力的作用效果可以替代这几个分力的作用效果,不能认为合力与分力同时作用在物体上,所以A、C正确,B不正确;求合力应遵循平行四边形定则,所以D正确.
二、合力的求解方法
1.作图法:要选取统一标度,严格作出力的图示以及平行四边形,用统一标度去度量作出的平行四边形的对角线,求出合力的大小,再量出对角线与某一分力的夹角,求出合力的方向.
2.计算法:设共点力F1、F2的夹角为θ,作出力的合成示意图(如图2-5-4),则F的大小等于OC的长度所对应的力的大小,F的方向与F1成α角.由图可看出,OC是平行四边形OACB的一条对角线,OC又是三角形OAC的一条边.可见,一旦作出了力的合成示意图,就将求解合力的物理问题转化成数学的几何问题了.
图2-5-4
图2-5-5
图2-5-6
特别提醒:(1)作图时,合力、分力要共点,实线、虚线要分清,标度要唯一且适当.
(2)作图法和计算法均为矢量运算的通用方法.
例1
两个共点力的大小分别为F1=15 N,F2=9 N,它们的合力不可能等于( )
A.9 N
B.25 N
C.6 N
D.21 N
课堂互动讲练
合力与分力的关系
【思路点拨】 解答本题时应注意以下三点:
(1)力的合成遵循平行四边形定则.
(2)两分力夹角越小,合力越大.
(3)合力的范围|F1-F2|≤F≤F1+F2.
【精讲精析】 两个力合成时,合力的范围是|F1-F2|≤F合≤F1+F2,即6 N≤F合≤24 N,由此可知,A、C、D可能,B不可能.
【答案】 B
变式训练1 小强的妈妈提一桶水,向上提起的力为150 N,小强和小勇接过来共同来提,关于小强和小勇的用力,下列说法正确的是( )
A.他俩必分别只用75 N的力
B.他俩可分别用100 N的力
C.他俩都可用小于75 N的力
D.他俩的力不可能大于75 N
解析:选B.小强和小勇两人用力的合力大小应为150 N,则两个分力不可能都小于75 N,应该大于等于75 N.
例2
合力的计算
一个物体受到大小相等的两个拉力作用,每个拉力都是100 N,夹角为90°,求这两个力的合力.
【思路点拨】 本题中的两个力大小相等,夹角为90°,所以可以用作图法和计算法来求解合力的大小.
【精讲精析】 法一(作图法):取5 mm长线段表示20 N,作出平行四边形如图2-5-7所示:量得对角线长为35 mm,则合力F大小为140 N,方向沿F1、F2夹角的平分线方向,与F1夹角为45°.
图2-5-7
图2-5-8
【答案】 140 N(或141.4 N) 方向与F1成45°
【方法总结】 (1)在利用作图法求解时,一定要注意各力均使用同一标度.
(2)计算法是根据平行四边形定则作出示意图,把力归结到一个三角形中,然后利用解三角形的方法求出合力(常用方法).
变式训练2 水平横梁一端插在墙壁内,另一端装小滑轮B.一轻绳的一端C固定于墙壁上,另一端跨过滑轮后悬挂一质量m=10 kg的重物,∠CBA=30°,如图2-5-9所示,则滑轮受到绳子的作用力为(g取10 N/kg)( )
图2-5-9
一物体受到同一平面内的三个共点力作用,其大小分别为:F1=30 N,F2=40 N,F3=50 N,则它们的合力的最大值与最小值分别是多少?
【思路点拨】 本题的难点是求合力的最小值,首先要判断出合力的最小值是否为0.
例3
三个力的合成问题
【自主解答】 当三个力方向相同时,其合力最大,最大值为:
Fmax=F1+F2+F3=120 N.
三个力中,较小的两个力是F1和F2,其二者的合力范围F2-F1≤F12≤F1+F2即10 N≤F12≤70 N,包括F3=50 N,所以三个力合力的最小值为零.
【答案】 120 N 0
【方法总结】 三个力合成时,当它们的方向相同时,合力最大,若三个力中较小的两个力的和大于等于第三个力,其差小于第三个力,则三个力的合力的最小值为零,若两个较小力的和小于第三个力,则三个力的合力的最小值等于第三个力减去两个较小力的和,方向与第三个力的方向相同.
变式训练3 物体同时受到同一平面内三个共点力的作用,下列几组力的合力不可能为零的是( )
A.5 N,7 N,8 N
B.5 N,2 N,3 N
C.1 N,5 N,10 N
D.10 N,10 N,10 N
解析:选C.三力合成时,若两个力的合力可与第三力大小相等、方向相反,就可以使这三个力的合力为零,只要第三力在其他两个力合力范围内,其合力就可能为零,即第三力F3要满足:|F1-F2|≤F3≤F1+F2.
A中前两力合力范围为2 N≤F合≤12 N,第三力在其范围内;B中,3 N≤F合≤7 N,第三力在其合力范围内;C中,4 N≤F合≤6 N,第三力不在其合力范围内;D中,0 N≤F合≤20 N,第三力在其合力范围内;故只有C项中,第三力不在前两力合力范围内,C项中的三力合力不可能为零.
知能优化训练
本部分内容讲解结束
点此进入课件目录
按ESC键退出全屏播放
谢谢使用
同课章节目录
- 第一章 运动的描述
- 1 质点 参考系 空间 时间
- 2 位置变化的描述——位移
- 3 运动快慢与方向的描述——速度
- 4 速度变化快慢的描述——加速度
- 5 匀变速直线运动速度与时间的关系
- 6 匀变速直线运动位移与时间的关系
- 7 对自由落体运动的研究
- 8 匀变速直线运动规律的应用
- 9 测定匀变速直线运动的加速度
- 第二章 力
- 1 力
- 2 重力
- 3 弹力
- 4 摩擦力
- 5 力的合成
- 6 力的分解
- 第三章 牛顿运动定律
- 1 牛顿第一定律
- 2 探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 牛顿第三定律
- 5 牛顿运动定律的应用
- 6 超重与失重
- 第四章 物体的平衡
- 1 共点力作用下物体的平衡
- 2 共点力平衡条件的应用
- 3 平衡的稳定性(选学)
