6.3 相似图形 课件(共31张PPT)
文档属性
| 名称 | 6.3 相似图形 课件(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-19 00:00:00 | ||
图片预览








文档简介
(共30张PPT)
6.3 相似图形
第6章 图形的相似
2020-2021学年度苏科版九年级下册
欣赏
下列各组图形有什么共同的特征?你还能举出具有这样特征的图形吗?
形状相同的图形叫做相似形(similar figures).
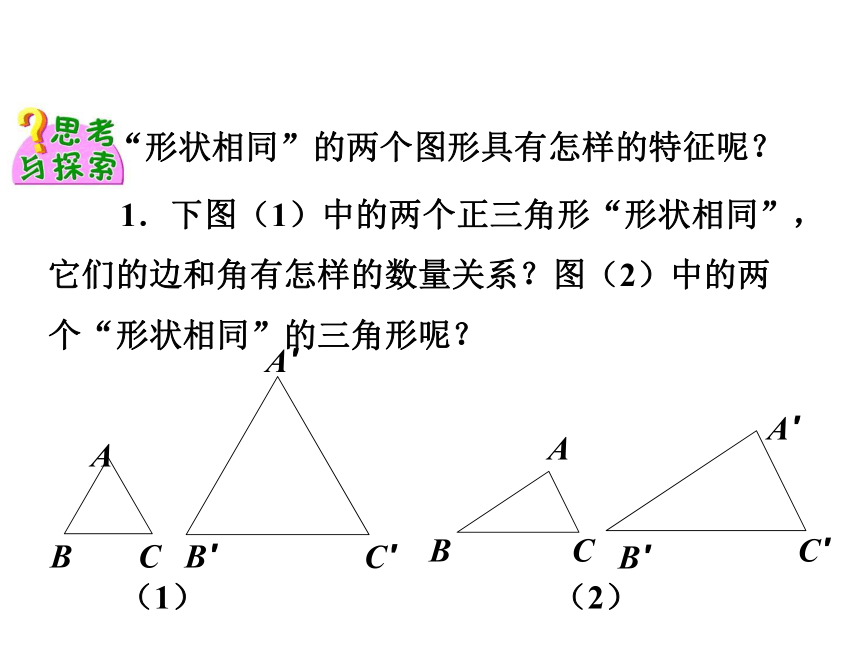
“形状相同”的两个图形具有怎样的特征呢?
1.下图(1)中的两个正三角形“形状相同”,它们的边和角有怎样的数量关系?图(2)中的两个“形状相同”的三角形呢?
C
B
A
A′
A′
A
B′
B
B′
C
C′
C′
(1)
(2)
“形状相同”的两个图形具有怎样的特征呢?
2.下图(1)中的两个正方形“形状相同”,它们的边和角有怎样的数量关系?图(2)中的两个“形状相同”的四边形呢?
C
B
A
A′
A′
A
B′
B
B′
C
C′
C′
(1)
(2)
D
D′
D
D′
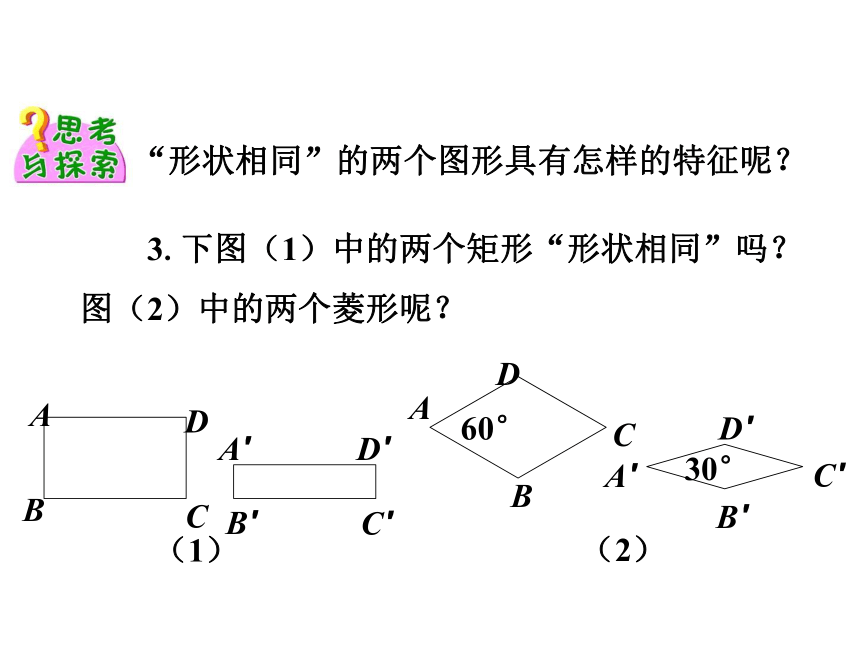
“形状相同”的两个图形具有怎样的特征呢?
3.下图(1)中的两个矩形“形状相同”吗?图(2)中的两个菱形呢?
C
B
A
A′
A′
A
B′
B
B′
C
C′
C′
(1)
(2)
D
D′
D
D′
60°
30°
“形状相同”的两个图形具有怎样的特征呢?
相似多边形的对应角相等,对应边成比例.
相似多边形的对应边的比叫做相似比(similarity ratio).
如何用数学语言描述两图形相似?表示两图形相似时有何需要注意的地方?从课本中找出答案吧!
例1 若下图中△ABC∽△A′B′C′.你能求出∠α的大小和A′C′的长吗?
6.3 相似图形
解:因为△ABC∽△ A′B′C′所以它们的对应角相等,对应边成比例.由此,得
∠ α= ∠A=60 °,
例2 如图,D、E、F分别是△ABC三边的中点,△DEF与△ABC相似吗?为什么?
6.3 相似图形
解:由三角形中位线的性质,知
EF∥BC,DE∥AB,DF∥AC;
EF= BC,DE= AB,DF= AC.
于是,在□AFDE、□BDEF、□CEFD中,
∠EDF=∠A,∠DEF=∠B,∠DFE=∠C.
又因为
所以△DEF∽△ABC.
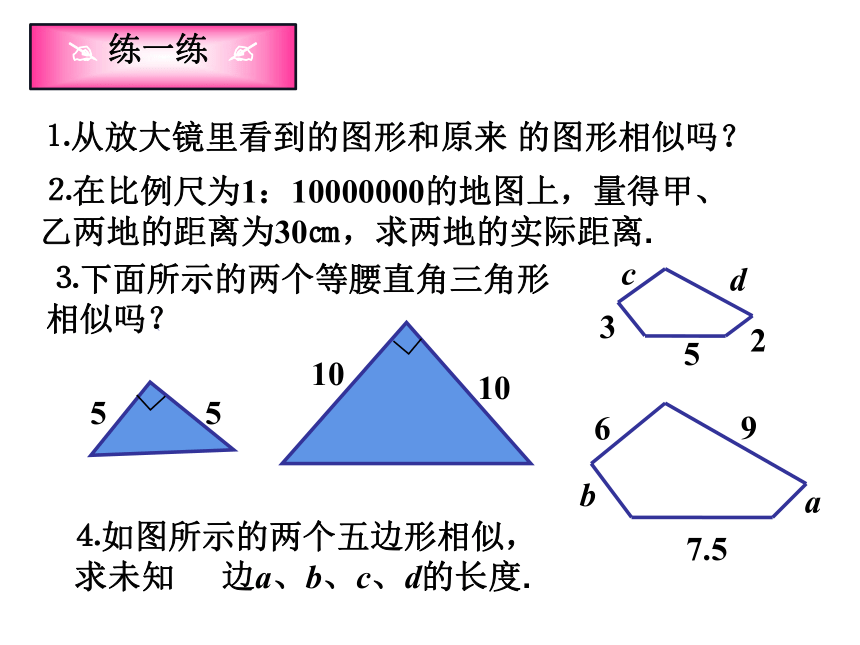
练一练
⒈从放大镜里看到的图形和原来 的图形相似吗?
⒉在比例尺为1:10000000的地图上,量得甲、 乙两地的距离为30㎝,求两地的实际距离.
⒊下面所示的两个等腰直角三角形相似吗?
⒋如图所示的两个五边形相似,求未知 边a、b、c、d的长度.
c
3
5
2
d
6
b
7.5
a
9
5
5
10
10
∟
∟
A
B
C
D
E
F
G
H
21 ㎝
18 ㎝
24 ㎝
β
α
X
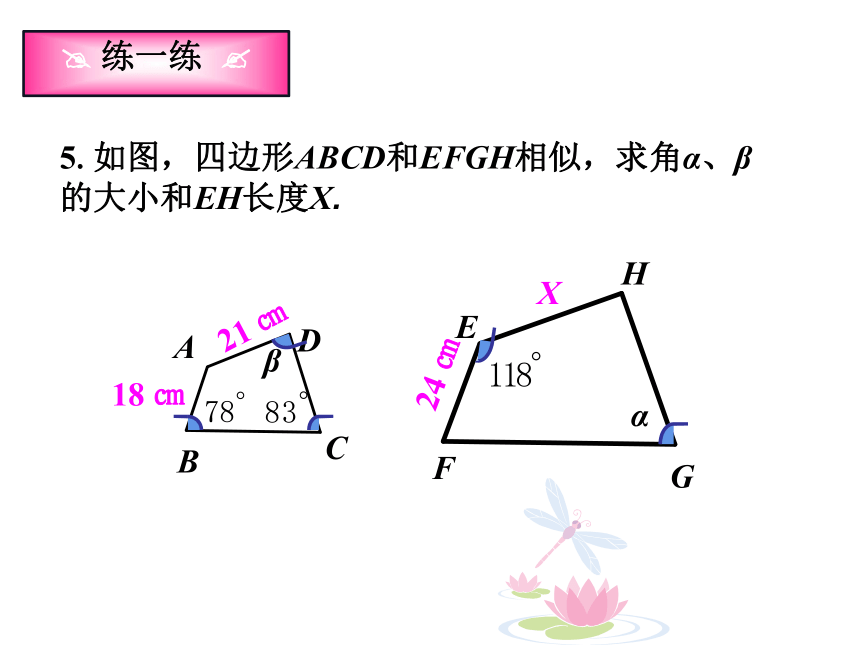
5.如图,四边形ABCD和EFGH相似,求角α、β的大小和EH长度X.
练一练
在四边形ABCD中,
解得 X=28(㎝)
解:四边形ABCD和EFGH相似,它们的对应角相等,由此可得
四边形ABCD和EFGH相似,它们对应边的比相等.由此可得
∠α=∠C ∠A=∠E=118°
∠β=360°-(78°+83°+118°)=81°
你能说一说上述图片的共同之处吗?
它们的大小不一定相等,但形状相同.
形状相同的图形叫做相似图形.
思考:
全等图形是特殊的相似图形.全等一定相似,但相似不一定全等.
全等图形和相似图形之间有什么联系与区别
判断:下面各组图形中,哪组图形是相似图形?
为什么?
(1)
(2)
(3)
1.对应角相等,对应边成比例的两个多边形,它们的形状相同,称为相似多边形.
2.相似多边形的性质:
相似多边形的对应角相等,对应边成比例.
3.相似多边形的表示方法:
四边形ABCD与A′B′C′D′相似,记作:四边形ABCD∽A′B′C′D′.
A
B
C
D
注意:表示对应顶点的字母一定要写在对应位置上.
4.相似多边形的对应边的比叫做相似比.
5.根据相似多边形的概念,我们不难得到:对应角相等,对应边成比例的两个三角形叫做相似三角形.
6.相似三角形的性质:相似三角形的对应角相等,对应边成比例.
表示对应顶点的字母要写在对应的位置上.
A
B
C
A'
B'
C'
则△ABC与△A'B'C'相似,记作
△ABC∽△ A'B'C' ,其中k叫做它们的相似比.
看谁反应快
下面每组都有两个三角形相似,请把它们表示出来,并说出它们的相似比.
△ABC∽ △ A'B'C'
△ABC与 △ A'B'C' 的相似
比为
△ABC∽ △DEF
△DEF与 △ABC的
相似比为
2
①
1.5
3
1.5
②
2
4
2
看谁反应快
△ADE∽△ ABC
△ADE与 △ ABC 的相似
比为
△AOB∽△ COD
△AOB与 △ COD 的相似
比为
2
1
1
3
2
如图,△ABC ∽△A' B' C' ,求∠α的大小和A' C'的长.
8
B
C
10
60°
A
α
C'
6
A'
B'
解:∵ △ABC ∽△ A' B' C' ,
∴∠α= ∠A=60.
(相似三角形的对应角相等)
(相似三角形的对应边成比例)
∴
例1
如图,D、E、F分别是△ABC三边的
中点,△DEF与△ABC相似吗?为什么?
解: △DEF ∽ △ABC.
由三角形中位线性质,得
EF= BC,DE= AB,DF = AC.
∴∠EDF=∠ A ,∠ DEF= ∠B,∠ DFE= ∠ C.
∴四边形AFDE、四边形BDEF、四边形CEFD是平行四边形.
EF∥BC, DE ∥ AB, DF ∥ AC.
∴
又由三角形中位线性质,可知
∴ △DEF ∽ △ABC.
例2
练一练
1.从放大镜里看到的图形和原来 的图形相似吗?
2.在比例尺为1:10000000的地图上,量得甲、 乙两地的距离为30㎝,求两地的实际距离.
3.下面所示的两个等腰直角三角形相似吗?
5
5
10
10
∟
∟
练一练
4.若a,b,c,d成比例,且a=2,b=3,c=4,那么d等于多少?
解: ∵a,b,c,d成比例
又∵a=2 b=3 c=4
解得 d=6.
∴即
相似图形:
注:它是由一个图形放大或缩小的一种图形变换,图形放大或缩小的倍数就是相似比
相似多边形的定义及性质:
相似比:
对应角相等地,对应边的比相等
相似多边形对应边的比
反过来,即相似多边形的定义
是形状相同的图形
成比例线段:
数学的研究方法:
由特殊到一般
由简单到复杂
学习了一种求线段长度的方法:
根据相似列比例式
谢谢聆听
6.3 相似图形
第6章 图形的相似
2020-2021学年度苏科版九年级下册
欣赏
下列各组图形有什么共同的特征?你还能举出具有这样特征的图形吗?
形状相同的图形叫做相似形(similar figures).
“形状相同”的两个图形具有怎样的特征呢?
1.下图(1)中的两个正三角形“形状相同”,它们的边和角有怎样的数量关系?图(2)中的两个“形状相同”的三角形呢?
C
B
A
A′
A′
A
B′
B
B′
C
C′
C′
(1)
(2)
“形状相同”的两个图形具有怎样的特征呢?
2.下图(1)中的两个正方形“形状相同”,它们的边和角有怎样的数量关系?图(2)中的两个“形状相同”的四边形呢?
C
B
A
A′
A′
A
B′
B
B′
C
C′
C′
(1)
(2)
D
D′
D
D′
“形状相同”的两个图形具有怎样的特征呢?
3.下图(1)中的两个矩形“形状相同”吗?图(2)中的两个菱形呢?
C
B
A
A′
A′
A
B′
B
B′
C
C′
C′
(1)
(2)
D
D′
D
D′
60°
30°
“形状相同”的两个图形具有怎样的特征呢?
相似多边形的对应角相等,对应边成比例.
相似多边形的对应边的比叫做相似比(similarity ratio).
如何用数学语言描述两图形相似?表示两图形相似时有何需要注意的地方?从课本中找出答案吧!
例1 若下图中△ABC∽△A′B′C′.你能求出∠α的大小和A′C′的长吗?
6.3 相似图形
解:因为△ABC∽△ A′B′C′所以它们的对应角相等,对应边成比例.由此,得
∠ α= ∠A=60 °,
例2 如图,D、E、F分别是△ABC三边的中点,△DEF与△ABC相似吗?为什么?
6.3 相似图形
解:由三角形中位线的性质,知
EF∥BC,DE∥AB,DF∥AC;
EF= BC,DE= AB,DF= AC.
于是,在□AFDE、□BDEF、□CEFD中,
∠EDF=∠A,∠DEF=∠B,∠DFE=∠C.
又因为
所以△DEF∽△ABC.
练一练
⒈从放大镜里看到的图形和原来 的图形相似吗?
⒉在比例尺为1:10000000的地图上,量得甲、 乙两地的距离为30㎝,求两地的实际距离.
⒊下面所示的两个等腰直角三角形相似吗?
⒋如图所示的两个五边形相似,求未知 边a、b、c、d的长度.
c
3
5
2
d
6
b
7.5
a
9
5
5
10
10
∟
∟
A
B
C
D
E
F
G
H
21 ㎝
18 ㎝
24 ㎝
β
α
X
5.如图,四边形ABCD和EFGH相似,求角α、β的大小和EH长度X.
练一练
在四边形ABCD中,
解得 X=28(㎝)
解:四边形ABCD和EFGH相似,它们的对应角相等,由此可得
四边形ABCD和EFGH相似,它们对应边的比相等.由此可得
∠α=∠C ∠A=∠E=118°
∠β=360°-(78°+83°+118°)=81°
你能说一说上述图片的共同之处吗?
它们的大小不一定相等,但形状相同.
形状相同的图形叫做相似图形.
思考:
全等图形是特殊的相似图形.全等一定相似,但相似不一定全等.
全等图形和相似图形之间有什么联系与区别
判断:下面各组图形中,哪组图形是相似图形?
为什么?
(1)
(2)
(3)
1.对应角相等,对应边成比例的两个多边形,它们的形状相同,称为相似多边形.
2.相似多边形的性质:
相似多边形的对应角相等,对应边成比例.
3.相似多边形的表示方法:
四边形ABCD与A′B′C′D′相似,记作:四边形ABCD∽A′B′C′D′.
A
B
C
D
注意:表示对应顶点的字母一定要写在对应位置上.
4.相似多边形的对应边的比叫做相似比.
5.根据相似多边形的概念,我们不难得到:对应角相等,对应边成比例的两个三角形叫做相似三角形.
6.相似三角形的性质:相似三角形的对应角相等,对应边成比例.
表示对应顶点的字母要写在对应的位置上.
A
B
C
A'
B'
C'
则△ABC与△A'B'C'相似,记作
△ABC∽△ A'B'C' ,其中k叫做它们的相似比.
看谁反应快
下面每组都有两个三角形相似,请把它们表示出来,并说出它们的相似比.
△ABC∽ △ A'B'C'
△ABC与 △ A'B'C' 的相似
比为
△ABC∽ △DEF
△DEF与 △ABC的
相似比为
2
①
1.5
3
1.5
②
2
4
2
看谁反应快
△ADE∽△ ABC
△ADE与 △ ABC 的相似
比为
△AOB∽△ COD
△AOB与 △ COD 的相似
比为
2
1
1
3
2
如图,△ABC ∽△A' B' C' ,求∠α的大小和A' C'的长.
8
B
C
10
60°
A
α
C'
6
A'
B'
解:∵ △ABC ∽△ A' B' C' ,
∴∠α= ∠A=60.
(相似三角形的对应角相等)
(相似三角形的对应边成比例)
∴
例1
如图,D、E、F分别是△ABC三边的
中点,△DEF与△ABC相似吗?为什么?
解: △DEF ∽ △ABC.
由三角形中位线性质,得
EF= BC,DE= AB,DF = AC.
∴∠EDF=∠ A ,∠ DEF= ∠B,∠ DFE= ∠ C.
∴四边形AFDE、四边形BDEF、四边形CEFD是平行四边形.
EF∥BC, DE ∥ AB, DF ∥ AC.
∴
又由三角形中位线性质,可知
∴ △DEF ∽ △ABC.
例2
练一练
1.从放大镜里看到的图形和原来 的图形相似吗?
2.在比例尺为1:10000000的地图上,量得甲、 乙两地的距离为30㎝,求两地的实际距离.
3.下面所示的两个等腰直角三角形相似吗?
5
5
10
10
∟
∟
练一练
4.若a,b,c,d成比例,且a=2,b=3,c=4,那么d等于多少?
解: ∵a,b,c,d成比例
又∵a=2 b=3 c=4
解得 d=6.
∴即
相似图形:
注:它是由一个图形放大或缩小的一种图形变换,图形放大或缩小的倍数就是相似比
相似多边形的定义及性质:
相似比:
对应角相等地,对应边的比相等
相似多边形对应边的比
反过来,即相似多边形的定义
是形状相同的图形
成比例线段:
数学的研究方法:
由特殊到一般
由简单到复杂
学习了一种求线段长度的方法:
根据相似列比例式
谢谢聆听
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
