6.4 探索三角形相似的条件(第3课时) 课件(共30张PPT)
文档属性
| 名称 | 6.4 探索三角形相似的条件(第3课时) 课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-19 18:09:53 | ||
图片预览





文档简介
6.4 探索三角形相似的条件
(第3课时)
第6章 图形的相似
2020-2021学年度苏科版九年级下册
回顾复习
三角形相似的判定定理1:
两角分别相等的两个三角形相似.
三角形相似的判定定理2:
两边成比例且夹角相等的两个三角形相似.
我们学过哪些三角形相似定理?
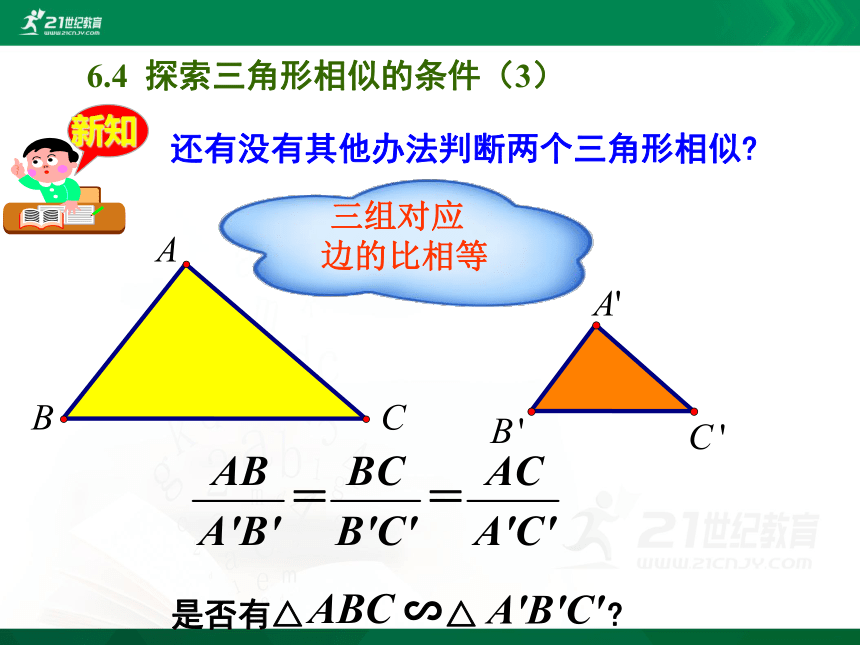
三组对应
边的比相等
是否有△ ∽△ ?
还有没有其他办法判断两个三角形相似?
新知
6.4 探索三角形相似的条件(3)
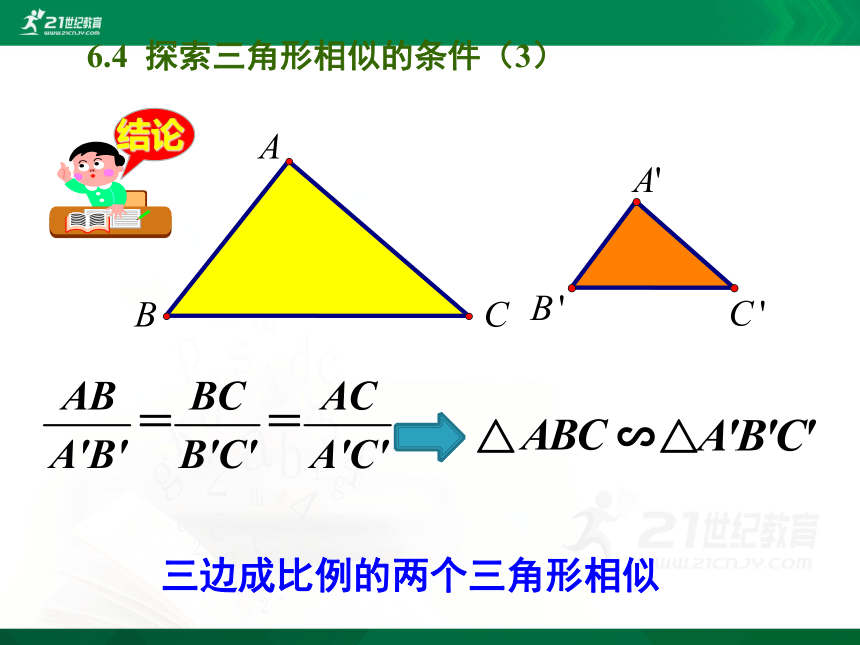
△ ∽△
结论
三边成比例的两个三角形相似
6.4 探索三角形相似的条件(3)
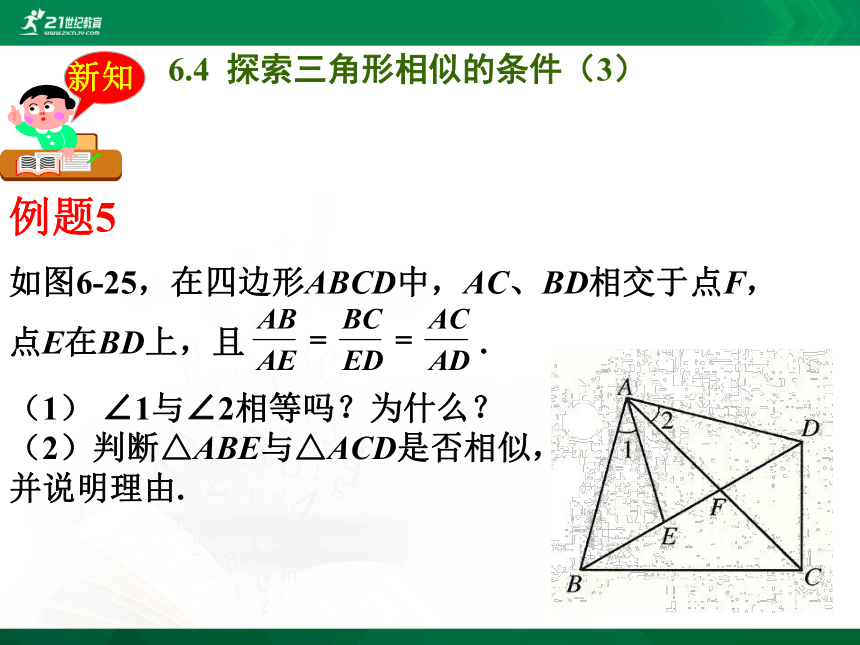
例题5
新知
6.4 探索三角形相似的条件(3)
如图6-25,在四边形ABCD中,AC、BD相交于点F,点E在BD上,且 .
(1) ∠1与∠2相等吗?为什么?
(2)判断△ABE与△ACD是否相似,并说明理由.
解:(1) ∠1与∠2相等. 在△ABC和△AED中,
∵
∴ △ABC ∽ △AED(三边成比例的两个三角形相似).
∴ ∠BAC= ∠EAD(相似三角形的对应角相等).
∴ ∠1= ∠2.
(2) △ABE与△ACD相似.
由 ,得 .
在△ABE和△ACD中,
∵ , ∠1= ∠2,
∴ △ ABE ∽ △ACD(两边成比例且夹角相等的两个三角形相似).
如何识别两三角形是否相似?
平行于三角形一边的直线和其他两边相交,所截得的三角形与原三角形相似.
定义:两三角形对应角相等,对应边的比相等的两个三角形相似.
两角分别相等的两个三角形相似.
两边成比例且夹角相等的两个三角形相似.
三边成比例的两个三角形相似.
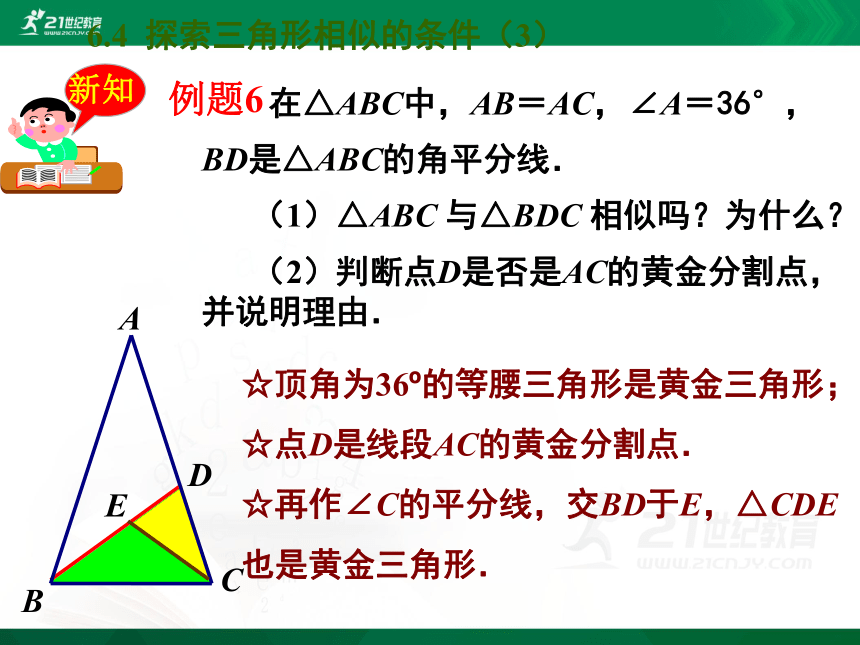
在△ABC中,AB=AC,∠A=36°,
BD是△ABC的角平分线.
(1)△ABC 与△BDC 相似吗?为什么?
(2)判断点D是否是AC的黄金分割点,并说明理由.
D
C
A
B
E
☆顶角为36?的等腰三角形是黄金三角形;
☆点D是线段AC的黄金分割点.
☆再作∠C的平分线,交BD于E,△CDE也是黄金三角形.
新知
6.4 探索三角形相似的条件(3)
例题6
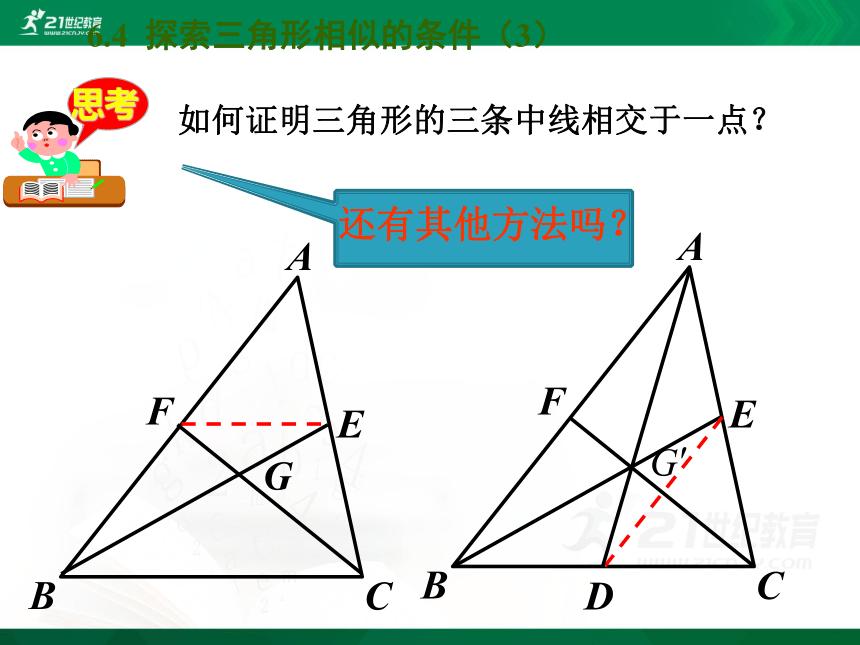
如何证明三角形的三条中线相交于一点?
C
B
A
F
G
E
还有其他方法吗?
思考
C
B
A
E
D
F
6.4 探索三角形相似的条件(3)
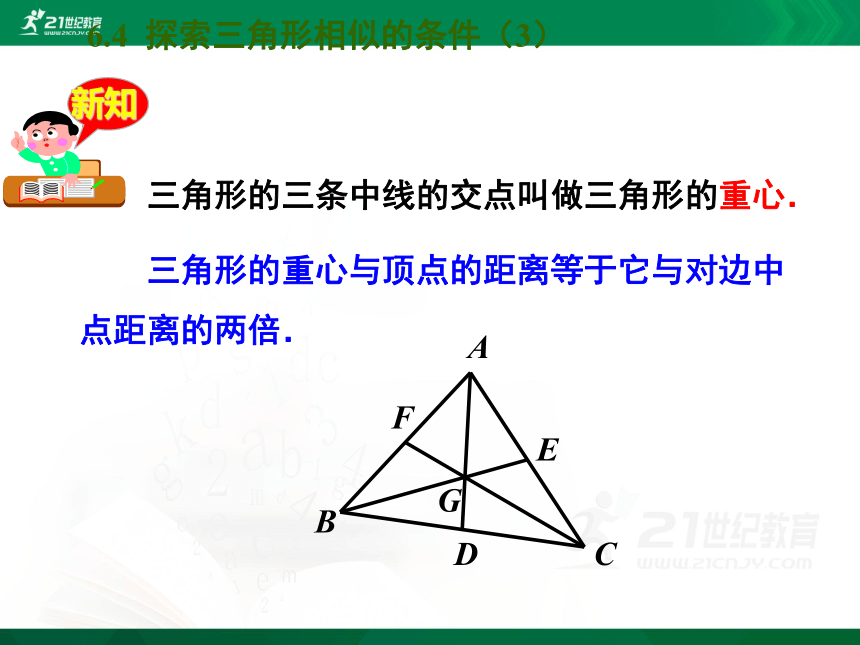
三角形的重心与顶点的距离等于它与对边中点距离的两倍.
三角形的三条中线的交点叫做三角形的重心.
A
B
C
G
D
E
F
新知
6.4 探索三角形相似的条件(3)
有一池塘, 周围都是空地.如果要测量池塘两端A、B间的距离,你能利用本节所学的知识解决这个问题吗?
A
B
尝试
6.4 探索三角形相似的条件(3)
A
D
C
E
B
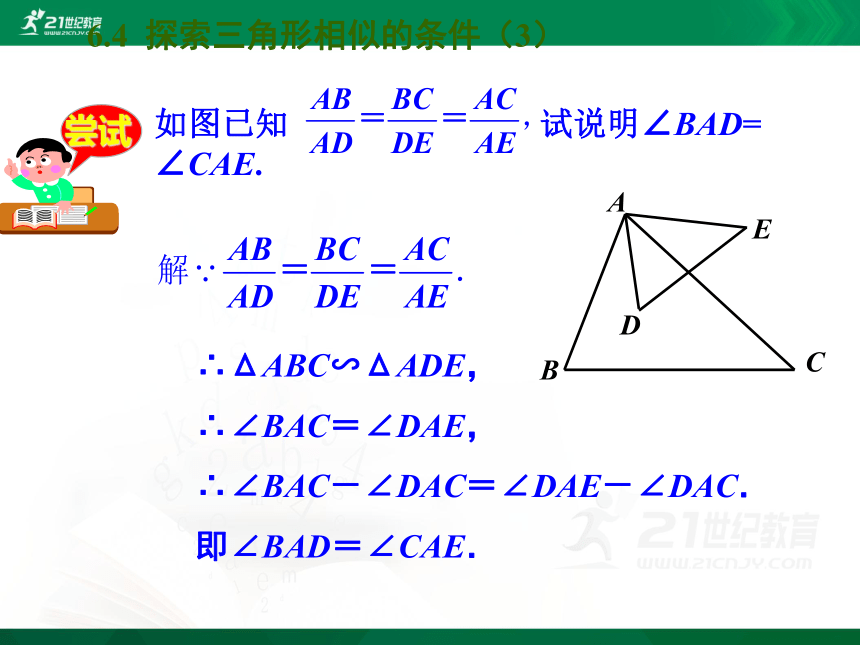
∴ΔABC∽ΔADE,
∴∠BAC=∠DAE,
∴∠BAC-∠DAC=∠DAE-∠DAC.
即∠BAD=∠CAE.
尝试
6.4 探索三角形相似的条件(3)
如图已知 试说明∠BAD= ∠CAE.
△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.△ABC与△ DEF相似吗?为什么?
尝试
A
B
C
F
E
D
还有其他方法吗?
6.4 探索三角形相似的条件(3)
∴
∵
∴
△ABC∽△A′B′C′
解:
尝试
根据下列条件,判断△ABC△A′B′C′是否相似,并说明理由.
AB=3,BC=5,AC=6;A′B′=6, B′C′=10,A′C′=12.
要制作两个形状相同的三角形框架,其中一个三角形框架的三边长分别为4,6,8.另一个三角形框架的一边长为2,它的另外两条边长应当是多少?你有几种答案?
提示:三种选法,分别使另一个三角形的长为2的边与长为4,6,8的边对应.
2:4=x:6=y:8
x:4=2:6=y:8
x:4=y:6=2:8
尝试
4
5
6
2
6.4 探索三角形相似的条件(3)
回顾复习
三角形相似的判定定理1:
两角分别相等的两个三角形相似.
三角形相似的判定定理2:
两边成比例且夹角相等的两个三角形相似.
我们学过哪些三角形相似定理?
自主探究
在△ABC和 △ 中
当k=1时,
△ABC与△有怎样的关系?
当k ≠ 1时,
△ABC与△有怎样的关系?
符号语言:
归纳总结
判定两个三角形相似的方法3:
三边成比例的两个三角形相似.
△ ∽△
例题5
如图6-25,在四边形ABCD中,AC、BD相交于点F,点E在BD上,且 .
(1) ∠1与∠2相等吗?为什么?
(2)判断△ABE与△ACD是否相似,并说明理由.
典例分析
解:(1) ∠1与∠2相等. 在△ABC和△AED中,
∵
∴ △ABC ∽ △AED(三边成比例的两个三角形相似).
∴ ∠BAC= ∠EAD(相似三角形的对应角相等).
∴ ∠1= ∠2.
(2) △ABE与△ACD相似.
由 ,得 .
在△ABE和△ACD中,
∵ , ∠1= ∠2,
∴ △ ABE ∽ △ACD(两边成比例且夹角相等的两个三角形相似).
1.根据下列条件,判断△ABC与△ A'B' C'是否相似,
并说明理由:
AB=8, BC=9,AC=15;A'B' =16, B' C' =18,A'C' =30.
当堂检测
A
D
C
E
B
∴ΔABC∽ΔADE,
∴∠BAC=∠DAE,
∴∠BAC-∠DAC=∠DAE-∠DAC.
即∠BAD=∠CAE.
2.如图已知 试说明∠BAD= ∠CAE.
当堂检测
在△ABC中,AB=AC,∠A=36°,
BD是△ABC的角平分线.
(1)△ABC 与△BDC 相似吗?为什么?
(2)判断点D是否是AC的黄金分割点,并说明理由.
D
C
A
B
例题6
☆顶角为36?的等腰三角形是黄金三角形;
☆点D是线段AC的黄金分割点.
☆再作∠C的平分线,交BD于E,△CDE也是黄金三角形.
如何证明三角形的三条中线相交于一点?
C
B
A
F
G
E
C
B
A
E
D
F
问题探究
三角形的重心与顶点的距离等于它与对边中点距离的两倍.
三角形的三条中线的交点叫做三角形的重心.
A
B
C
G
D
E
F
总结归纳
1.△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.△ABC与△ DEF相似吗?为什么?
尝试
A
B
C
F
E
D
还有其他方法吗?
巩固练习
∴
∵
∴
△ABC ∽ △A′B′C′
解:
2.根据下列条件,判断△ABC△A′B′C′是否相似,并说明理由.
AB=3,BC=5,AC=6;A′B′=6, B′C′=10,A′C′=12.
小结:
判定两个三角形相似的方法:
(1)平行于三角形一边的直线与其它两边相交,所得的三角形与与原三角形相似.
(2)两角分别相等的两个三角形相似.
(3)两边对应成比例且夹角相等的两个三角形相似.
(4)三边成比例的两个三角形相似.
三角形的三条中线的交点叫做三角形的重心.
谢谢聆听
(第3课时)
第6章 图形的相似
2020-2021学年度苏科版九年级下册
回顾复习
三角形相似的判定定理1:
两角分别相等的两个三角形相似.
三角形相似的判定定理2:
两边成比例且夹角相等的两个三角形相似.
我们学过哪些三角形相似定理?
三组对应
边的比相等
是否有△ ∽△ ?
还有没有其他办法判断两个三角形相似?
新知
6.4 探索三角形相似的条件(3)
△ ∽△
结论
三边成比例的两个三角形相似
6.4 探索三角形相似的条件(3)
例题5
新知
6.4 探索三角形相似的条件(3)
如图6-25,在四边形ABCD中,AC、BD相交于点F,点E在BD上,且 .
(1) ∠1与∠2相等吗?为什么?
(2)判断△ABE与△ACD是否相似,并说明理由.
解:(1) ∠1与∠2相等. 在△ABC和△AED中,
∵
∴ △ABC ∽ △AED(三边成比例的两个三角形相似).
∴ ∠BAC= ∠EAD(相似三角形的对应角相等).
∴ ∠1= ∠2.
(2) △ABE与△ACD相似.
由 ,得 .
在△ABE和△ACD中,
∵ , ∠1= ∠2,
∴ △ ABE ∽ △ACD(两边成比例且夹角相等的两个三角形相似).
如何识别两三角形是否相似?
平行于三角形一边的直线和其他两边相交,所截得的三角形与原三角形相似.
定义:两三角形对应角相等,对应边的比相等的两个三角形相似.
两角分别相等的两个三角形相似.
两边成比例且夹角相等的两个三角形相似.
三边成比例的两个三角形相似.
在△ABC中,AB=AC,∠A=36°,
BD是△ABC的角平分线.
(1)△ABC 与△BDC 相似吗?为什么?
(2)判断点D是否是AC的黄金分割点,并说明理由.
D
C
A
B
E
☆顶角为36?的等腰三角形是黄金三角形;
☆点D是线段AC的黄金分割点.
☆再作∠C的平分线,交BD于E,△CDE也是黄金三角形.
新知
6.4 探索三角形相似的条件(3)
例题6
如何证明三角形的三条中线相交于一点?
C
B
A
F
G
E
还有其他方法吗?
思考
C
B
A
E
D
F
6.4 探索三角形相似的条件(3)
三角形的重心与顶点的距离等于它与对边中点距离的两倍.
三角形的三条中线的交点叫做三角形的重心.
A
B
C
G
D
E
F
新知
6.4 探索三角形相似的条件(3)
有一池塘, 周围都是空地.如果要测量池塘两端A、B间的距离,你能利用本节所学的知识解决这个问题吗?
A
B
尝试
6.4 探索三角形相似的条件(3)
A
D
C
E
B
∴ΔABC∽ΔADE,
∴∠BAC=∠DAE,
∴∠BAC-∠DAC=∠DAE-∠DAC.
即∠BAD=∠CAE.
尝试
6.4 探索三角形相似的条件(3)
如图已知 试说明∠BAD= ∠CAE.
△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.△ABC与△ DEF相似吗?为什么?
尝试
A
B
C
F
E
D
还有其他方法吗?
6.4 探索三角形相似的条件(3)
∴
∵
∴
△ABC∽△A′B′C′
解:
尝试
根据下列条件,判断△ABC△A′B′C′是否相似,并说明理由.
AB=3,BC=5,AC=6;A′B′=6, B′C′=10,A′C′=12.
要制作两个形状相同的三角形框架,其中一个三角形框架的三边长分别为4,6,8.另一个三角形框架的一边长为2,它的另外两条边长应当是多少?你有几种答案?
提示:三种选法,分别使另一个三角形的长为2的边与长为4,6,8的边对应.
2:4=x:6=y:8
x:4=2:6=y:8
x:4=y:6=2:8
尝试
4
5
6
2
6.4 探索三角形相似的条件(3)
回顾复习
三角形相似的判定定理1:
两角分别相等的两个三角形相似.
三角形相似的判定定理2:
两边成比例且夹角相等的两个三角形相似.
我们学过哪些三角形相似定理?
自主探究
在△ABC和 △ 中
当k=1时,
△ABC与△有怎样的关系?
当k ≠ 1时,
△ABC与△有怎样的关系?
符号语言:
归纳总结
判定两个三角形相似的方法3:
三边成比例的两个三角形相似.
△ ∽△
例题5
如图6-25,在四边形ABCD中,AC、BD相交于点F,点E在BD上,且 .
(1) ∠1与∠2相等吗?为什么?
(2)判断△ABE与△ACD是否相似,并说明理由.
典例分析
解:(1) ∠1与∠2相等. 在△ABC和△AED中,
∵
∴ △ABC ∽ △AED(三边成比例的两个三角形相似).
∴ ∠BAC= ∠EAD(相似三角形的对应角相等).
∴ ∠1= ∠2.
(2) △ABE与△ACD相似.
由 ,得 .
在△ABE和△ACD中,
∵ , ∠1= ∠2,
∴ △ ABE ∽ △ACD(两边成比例且夹角相等的两个三角形相似).
1.根据下列条件,判断△ABC与△ A'B' C'是否相似,
并说明理由:
AB=8, BC=9,AC=15;A'B' =16, B' C' =18,A'C' =30.
当堂检测
A
D
C
E
B
∴ΔABC∽ΔADE,
∴∠BAC=∠DAE,
∴∠BAC-∠DAC=∠DAE-∠DAC.
即∠BAD=∠CAE.
2.如图已知 试说明∠BAD= ∠CAE.
当堂检测
在△ABC中,AB=AC,∠A=36°,
BD是△ABC的角平分线.
(1)△ABC 与△BDC 相似吗?为什么?
(2)判断点D是否是AC的黄金分割点,并说明理由.
D
C
A
B
例题6
☆顶角为36?的等腰三角形是黄金三角形;
☆点D是线段AC的黄金分割点.
☆再作∠C的平分线,交BD于E,△CDE也是黄金三角形.
如何证明三角形的三条中线相交于一点?
C
B
A
F
G
E
C
B
A
E
D
F
问题探究
三角形的重心与顶点的距离等于它与对边中点距离的两倍.
三角形的三条中线的交点叫做三角形的重心.
A
B
C
G
D
E
F
总结归纳
1.△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.△ABC与△ DEF相似吗?为什么?
尝试
A
B
C
F
E
D
还有其他方法吗?
巩固练习
∴
∵
∴
△ABC ∽ △A′B′C′
解:
2.根据下列条件,判断△ABC△A′B′C′是否相似,并说明理由.
AB=3,BC=5,AC=6;A′B′=6, B′C′=10,A′C′=12.
小结:
判定两个三角形相似的方法:
(1)平行于三角形一边的直线与其它两边相交,所得的三角形与与原三角形相似.
(2)两角分别相等的两个三角形相似.
(3)两边对应成比例且夹角相等的两个三角形相似.
(4)三边成比例的两个三角形相似.
三角形的三条中线的交点叫做三角形的重心.
谢谢聆听
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
