6.5 相似三角形的性质 课件(共30张PPT)
文档属性
| 名称 | 6.5 相似三角形的性质 课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-19 18:12:24 | ||
图片预览







文档简介
6.5 相似三角形的性质
第6章 图形的相似
2020-2021学年度苏科版九年级下册
如图6-29,我们已经知道,当D、E、F分别是△ABC各边的中点时, △DEF∽ △ ABC,相似比为 . 这两个三角形的周长、面积之间有什么关系?
如果△ABC∽△A'B'C',相似比为k,那么
因此,
AB=k A'B',BC=kB'C',CA=kC'A',
从而
?
观察与思考
得到:
定理:相似三角形周长的比等于相似比.
定理:相似多边形周长的比等于相似比.
类似的,
探究
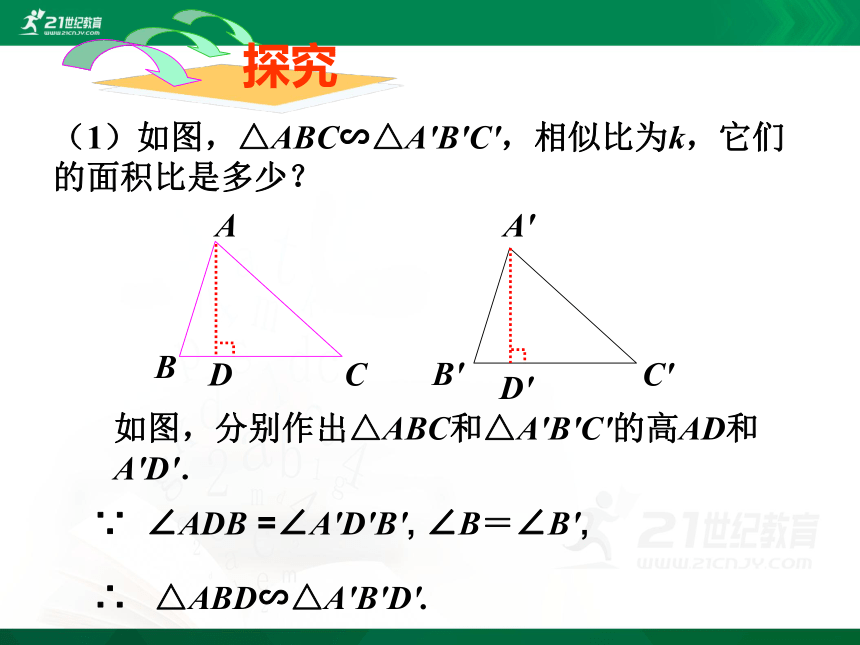
(1)如图,△ABC∽△A'B'C',相似比为k,它们的面积比是多少?
A
B
C
A'
B'
C'
D'
D
如图,分别作出△ABC和△A'B'C'的高AD和A'D'.
∵ ∠ADB =∠A'D'B', ∠B=∠B',
∴ △ABD∽△A'B'D'.
这样,得到:
定理:相似三角形面积的比等于相似比的平方.
类似的,得到:
定理:相似多边形的面积比等于相似比的平方.
例1 在比例尺为1:500的地图上,测得一个三角形地块ABC的周长为12cm,面积为6 cm2,求这个地块的实际周长和面积.
解:如果把实际三角形地块记为△A'B'C'
,那么△ABC∽ △ A'B'C'且相似比为 k= .
于是 = (相似三角形周长的比等于相似比), =( ) 2(相似三角形面积的比等于相似比的平方).
∴△ A'B'C'的周长=12×500=6000(cm)=60m,
△ A'B'C'的面积=6×500=1500000(cm2)=150m2.
答:这个地块的实际周长为60m,面积为150m2.
△ABC的周长
△ A'B'C'的周长
△ABC的面积
△ A'B'C'的面积
那么
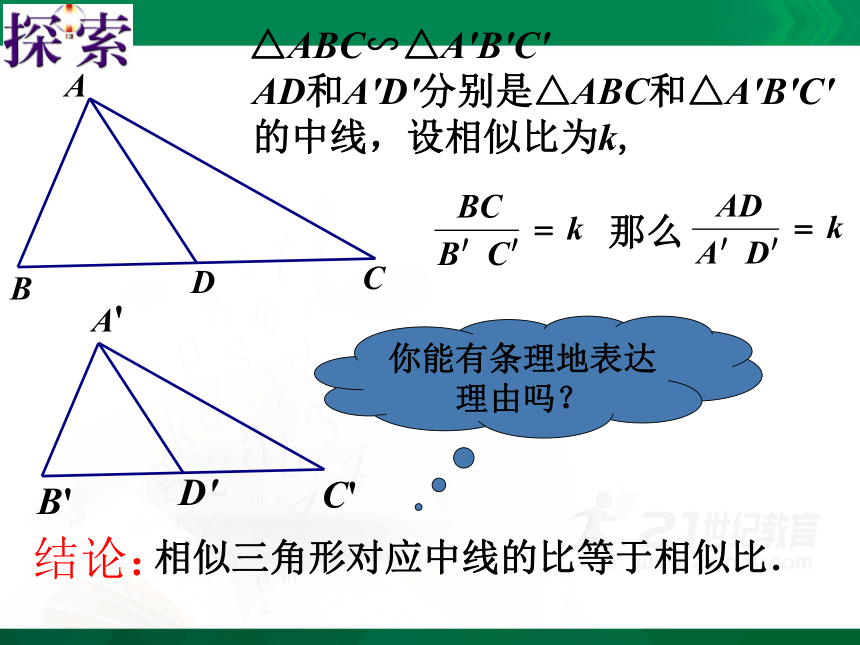
△ABC∽△A'B'C'
AD和A'D'分别是△ABC和△A'B'C'
的中线,设相似比为k,
D
A
B
C
D'
A'
B'
C'
相似三角形对应中线的比等于相似比.
结论:
你能有条理地表达理由吗?
D'
A'
B'
C'
D
A
B
C
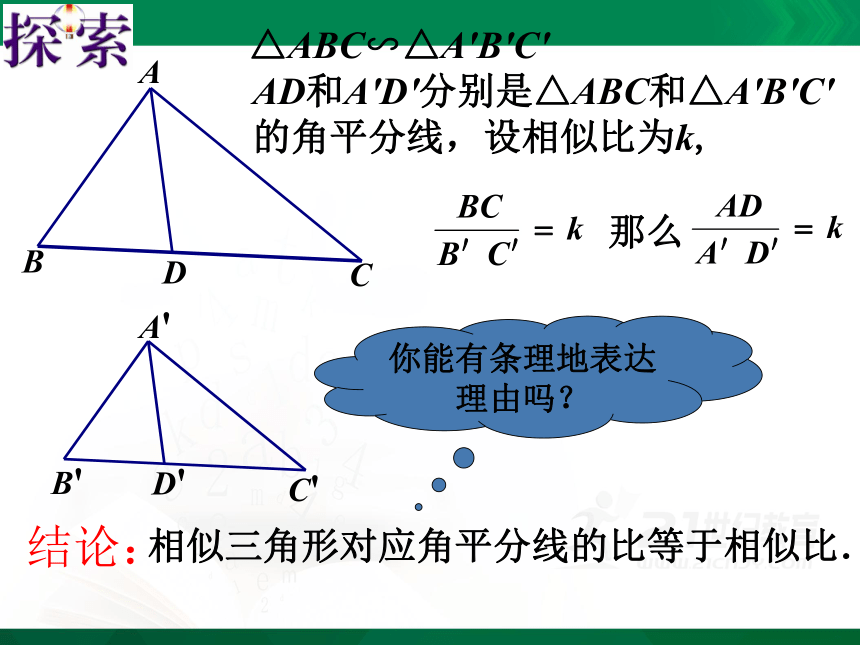
相似三角形对应角平分线的比等于相似比.
结论:
△ABC∽△A'B'C'
AD和A'D'分别是△ABC和△A'B'C'
的角平分线,设相似比为k,
你能有条理地表达理由吗?
那么
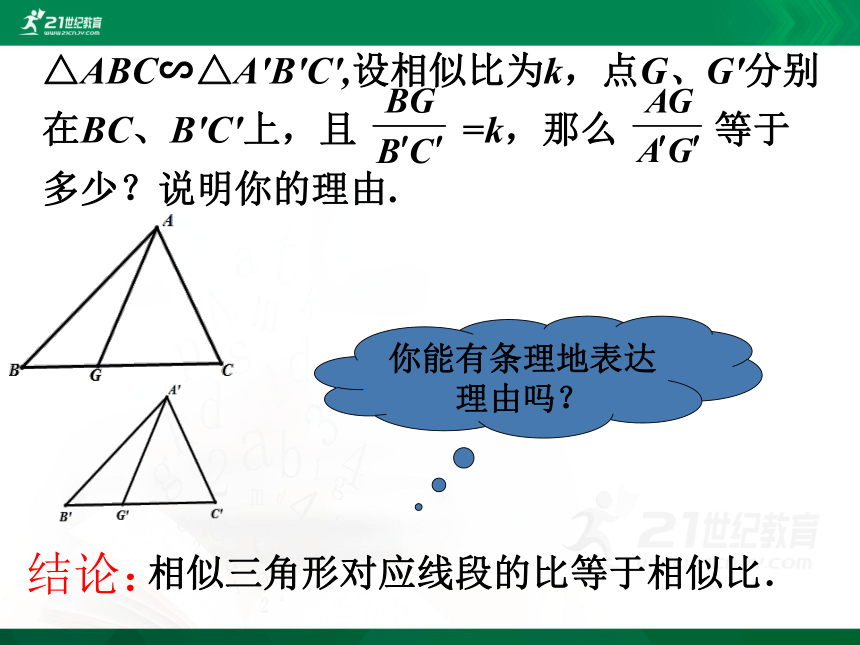
相似三角形对应线段的比等于相似比.
结论:
△ABC∽△A'B'C',设相似比为k,点G、G'分别在BC、B'C'上,且 =k,那么 等于多少?说明你的理由.
你能有条理地表达理由吗?
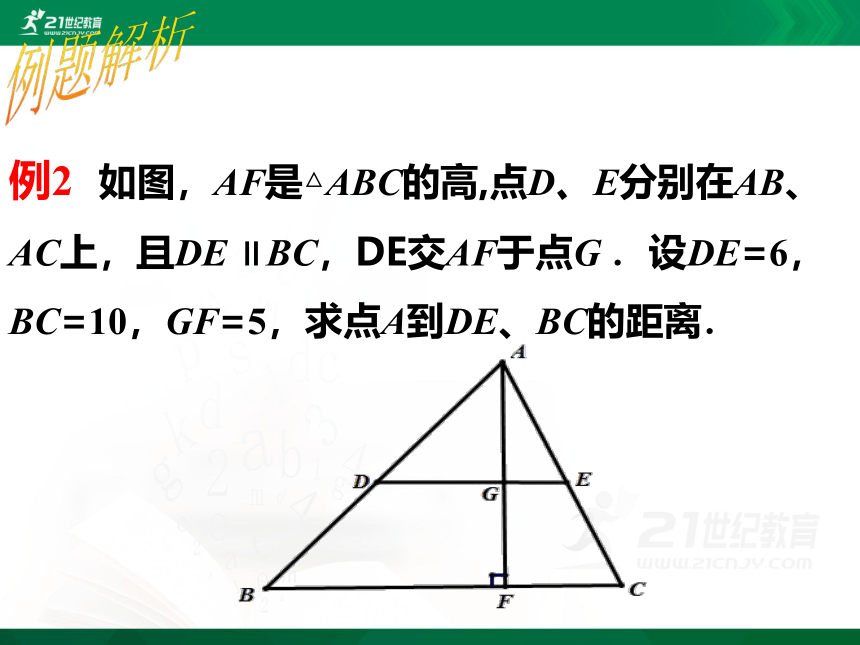
例2 如图,AF是△ABC的高,点D、E分别在AB、AC上,且DE ∥BC,DE交AF于点G .设DE=6,BC=10,GF=5,求点A到DE、BC的距离.
例题解析
解:由DE ∥BC, ∠AFB=90 °,得
∠AGD=90 °,即AG ⊥DE.
于是,AG、AF的长分别为点A到DE、BC的距离.
在△ADE和△ABC中,
∵DE ∥BC,
∴ △ADE ∽ △ABC.
∴ (相似三角形对应线段的比等于相似比),
即
由此,得AG=7.5,AF=AG+5=12.5,
即点A到DE、BC的距离分别为7.5、12.5.
当堂检测
1.如果两个相似多边形的面积比为1∶25,那么它们的相似比为( ).
A.1∶25 B.1∶5
C.1∶2.5 D.1∶50
2、填空题
(1)已知△ABC∽△A′B′C′的相似比为2︰3,
则它们对应中线的比为 ;
(2)已知两个相似三角形对应高的比是4︰1,
则它们的对应角平分线的比是 ;
(3)已知两个相似三角形对应角平分线的长分别为2 cm
和6cm ,其中一个三角形的周长18cm,则另一个三
角形的周长是 cm.
2︰3
4︰1
6或54
4.如图,有一批形状大小相同的不锈钢片,呈直角三角形,已知∠C=90°,AC=12cm,BC=5?cm,试设计一种方案,用这批不锈钢片裁出面积最大的正方形不锈钢片,并求出这种不锈钢片的边长.?
3.两个相似三角形的一组对应边长分别为3cm和5cm,且较小三角形的周长为15cm,那么较大三角形的周长为_________cm.
回顾复习
三角形相似的判定定理1:
两角分别相等的两个三角形相似.
三角形相似的判定定理2:
两边成比例且夹角相等的两个三角形相似.
我们学过哪些三角形相似定理?
三角形相似的判定定理3:
三边成比例的两个三角形相似.
A
B
C
A′
B′
C′
如图,已知△ABC∽△A′B′C′,相似比为k,则△ABC与△A′B′C′的周长比和面积比分别等于什么?怎么来说明?
课堂探讨
结论
性质1:相似三角形的周长比等于相似比;
性质2:相似三角形的面积比等于相似比的平方.
例1 在比例尺为1:500的地图上,测得一个三角形地块ABC的周长为12cm,面积为6 cm2,求这个地块的实际周长和面积.
解:如果把实际三角形地块记为△A'B'C'
,那么△ABC∽ △ A'B'C'且相似比为 k= .
于是 = (相似三角形周长的比等于相似比), =( ) 2(相似三角形面积的比等于相似比的平方).
∴△ A'B'C'的周长=12×500=6000(cm)=60m,
△ A'B'C'的面积=6×500=1500000(cm2)=150m2.
答:这个地块的实际周长为60m,面积为150m2.
△ABC的周长
△ A'B'C'的周长
△ABC的面积
△ A'B'C'的面积
四边形ABCD是平行四边形,点E是BC延长线上的一点,而且CE:BC=1:3,若△DGF的面积为9,试求:
(1)△ABG的面积;
(2) △ADG与△BGE的周长比与面积比;
A
B
C
D
E
F
G
拓展练习
D′
C′
D
A
B
C
A′
B′
△ABC∽△A'B'C'
AD和A'D'分别是△ABC和△A'B'C'
的高,设相似比为k,
┓
┓
相似三角形对应高的比等于相似比.
结论:
你能有条理地表达理由吗?
那么
D'
A'
B'
C'
D
A
B
C
相似三角形对应角平分线的比等于相似比.
结论:
△ABC∽△A'B'C'
AD和A'D'分别是△ABC和△A'B'C'
的角平分线,设相似比为k,
说明道理?
那么
△ABC∽△A'B'C'
AD和A'D'分别是△ABC和△A'B'C'
的中线,设相似比为k,
D
A
B
C
D'
A'
B'
C'
相似三角形对应中线的比等于相似比.
结论:
你能有条理地表达理由吗?
那么
例2 如图,AF是△ABC的高,点D、E分别在AB、AC上,且DE ∥BC,DE交AF于点G .设DE=6,BC=10,GF=5,求点A到DE、BC的距离.
例题解析
解:由DE ∥BC, ∠AFB=90°,得
∠AGD=90 °,即AG ⊥DE.
于是,AG、AF的长分别为点A到DE、BC的距离.
在△ADE和△ABC中,
∵DE ∥BC,
∴ △ADE ∽ △ABC.
∴ (相似三角形对应线段的比等于相似比),
即
由此,得AG=7.5,AF=AG+5=12.5,
即点A到DE、BC的距离分别为7.5、12.5.
1、? 两个相似三角形的相似比为2 : 3,它们的对应角平分线之比为________,周长之比为_______,面积之比为_________.
2、若两个三角形面积之比为16:9,则它们的对高之比为_____,对应中线之比为_____.
3、如图, △ABC∽ △DBA,D为BC上一点,E、F分别是AC、AD的中点,且AB=28cm,BC=36cm,则BE:BF=________.
A
B
F
D
C
E
2 : 3
2 : 3
4 : 9
4 : 3
4 : 3
9 : 7
4.如图, △ ABC的面积为25,直线DE平行于BC分别交AB、AC于点D、E.如果△ ADE的面积为9,求 的值.
拓展练习
建颍乡建造一新住宅小区,同时在小区旁筑一条马路.在施工中遇到这样一个问题,小区旁原来有一个面积是64平方米,周长44米的三角形的荒地,由于建筑马路这块地被削去了一块梯形,原荒地的一边AB的长由原来的12米缩短成9米.然后在剩下的荒地上种绿化,你能不用工具测量,计算出现在绿化地面积到底有多大?它的周长是多少?
课后思考
有一块三角形铁片ABC,BC=12cm,高AH=8cm,按下(1)、(2)两种设计方案把它加工成一块矩形铁片DEFG,且要求矩形的长是宽的2倍,为了减少浪费,加工成的矩形铁片的面积应尽量大些.请你通过计算判断(1)、(2)两种设计方案哪个更好?
课后思考
小结:
性质1:相似三角形的周长比等于相似比;
性质2:相似三角形的面积比等于相似比的平方.
性质 3:相似三角形对应高的比等于相似比.
性质 4:相似三角形对应角平分线的比等于相似比.
性质 5:相似三角形对应中线的比等于相似比.
谢谢聆听
第6章 图形的相似
2020-2021学年度苏科版九年级下册
如图6-29,我们已经知道,当D、E、F分别是△ABC各边的中点时, △DEF∽ △ ABC,相似比为 . 这两个三角形的周长、面积之间有什么关系?
如果△ABC∽△A'B'C',相似比为k,那么
因此,
AB=k A'B',BC=kB'C',CA=kC'A',
从而
?
观察与思考
得到:
定理:相似三角形周长的比等于相似比.
定理:相似多边形周长的比等于相似比.
类似的,
探究
(1)如图,△ABC∽△A'B'C',相似比为k,它们的面积比是多少?
A
B
C
A'
B'
C'
D'
D
如图,分别作出△ABC和△A'B'C'的高AD和A'D'.
∵ ∠ADB =∠A'D'B', ∠B=∠B',
∴ △ABD∽△A'B'D'.
这样,得到:
定理:相似三角形面积的比等于相似比的平方.
类似的,得到:
定理:相似多边形的面积比等于相似比的平方.
例1 在比例尺为1:500的地图上,测得一个三角形地块ABC的周长为12cm,面积为6 cm2,求这个地块的实际周长和面积.
解:如果把实际三角形地块记为△A'B'C'
,那么△ABC∽ △ A'B'C'且相似比为 k= .
于是 = (相似三角形周长的比等于相似比), =( ) 2(相似三角形面积的比等于相似比的平方).
∴△ A'B'C'的周长=12×500=6000(cm)=60m,
△ A'B'C'的面积=6×500=1500000(cm2)=150m2.
答:这个地块的实际周长为60m,面积为150m2.
△ABC的周长
△ A'B'C'的周长
△ABC的面积
△ A'B'C'的面积
那么
△ABC∽△A'B'C'
AD和A'D'分别是△ABC和△A'B'C'
的中线,设相似比为k,
D
A
B
C
D'
A'
B'
C'
相似三角形对应中线的比等于相似比.
结论:
你能有条理地表达理由吗?
D'
A'
B'
C'
D
A
B
C
相似三角形对应角平分线的比等于相似比.
结论:
△ABC∽△A'B'C'
AD和A'D'分别是△ABC和△A'B'C'
的角平分线,设相似比为k,
你能有条理地表达理由吗?
那么
相似三角形对应线段的比等于相似比.
结论:
△ABC∽△A'B'C',设相似比为k,点G、G'分别在BC、B'C'上,且 =k,那么 等于多少?说明你的理由.
你能有条理地表达理由吗?
例2 如图,AF是△ABC的高,点D、E分别在AB、AC上,且DE ∥BC,DE交AF于点G .设DE=6,BC=10,GF=5,求点A到DE、BC的距离.
例题解析
解:由DE ∥BC, ∠AFB=90 °,得
∠AGD=90 °,即AG ⊥DE.
于是,AG、AF的长分别为点A到DE、BC的距离.
在△ADE和△ABC中,
∵DE ∥BC,
∴ △ADE ∽ △ABC.
∴ (相似三角形对应线段的比等于相似比),
即
由此,得AG=7.5,AF=AG+5=12.5,
即点A到DE、BC的距离分别为7.5、12.5.
当堂检测
1.如果两个相似多边形的面积比为1∶25,那么它们的相似比为( ).
A.1∶25 B.1∶5
C.1∶2.5 D.1∶50
2、填空题
(1)已知△ABC∽△A′B′C′的相似比为2︰3,
则它们对应中线的比为 ;
(2)已知两个相似三角形对应高的比是4︰1,
则它们的对应角平分线的比是 ;
(3)已知两个相似三角形对应角平分线的长分别为2 cm
和6cm ,其中一个三角形的周长18cm,则另一个三
角形的周长是 cm.
2︰3
4︰1
6或54
4.如图,有一批形状大小相同的不锈钢片,呈直角三角形,已知∠C=90°,AC=12cm,BC=5?cm,试设计一种方案,用这批不锈钢片裁出面积最大的正方形不锈钢片,并求出这种不锈钢片的边长.?
3.两个相似三角形的一组对应边长分别为3cm和5cm,且较小三角形的周长为15cm,那么较大三角形的周长为_________cm.
回顾复习
三角形相似的判定定理1:
两角分别相等的两个三角形相似.
三角形相似的判定定理2:
两边成比例且夹角相等的两个三角形相似.
我们学过哪些三角形相似定理?
三角形相似的判定定理3:
三边成比例的两个三角形相似.
A
B
C
A′
B′
C′
如图,已知△ABC∽△A′B′C′,相似比为k,则△ABC与△A′B′C′的周长比和面积比分别等于什么?怎么来说明?
课堂探讨
结论
性质1:相似三角形的周长比等于相似比;
性质2:相似三角形的面积比等于相似比的平方.
例1 在比例尺为1:500的地图上,测得一个三角形地块ABC的周长为12cm,面积为6 cm2,求这个地块的实际周长和面积.
解:如果把实际三角形地块记为△A'B'C'
,那么△ABC∽ △ A'B'C'且相似比为 k= .
于是 = (相似三角形周长的比等于相似比), =( ) 2(相似三角形面积的比等于相似比的平方).
∴△ A'B'C'的周长=12×500=6000(cm)=60m,
△ A'B'C'的面积=6×500=1500000(cm2)=150m2.
答:这个地块的实际周长为60m,面积为150m2.
△ABC的周长
△ A'B'C'的周长
△ABC的面积
△ A'B'C'的面积
四边形ABCD是平行四边形,点E是BC延长线上的一点,而且CE:BC=1:3,若△DGF的面积为9,试求:
(1)△ABG的面积;
(2) △ADG与△BGE的周长比与面积比;
A
B
C
D
E
F
G
拓展练习
D′
C′
D
A
B
C
A′
B′
△ABC∽△A'B'C'
AD和A'D'分别是△ABC和△A'B'C'
的高,设相似比为k,
┓
┓
相似三角形对应高的比等于相似比.
结论:
你能有条理地表达理由吗?
那么
D'
A'
B'
C'
D
A
B
C
相似三角形对应角平分线的比等于相似比.
结论:
△ABC∽△A'B'C'
AD和A'D'分别是△ABC和△A'B'C'
的角平分线,设相似比为k,
说明道理?
那么
△ABC∽△A'B'C'
AD和A'D'分别是△ABC和△A'B'C'
的中线,设相似比为k,
D
A
B
C
D'
A'
B'
C'
相似三角形对应中线的比等于相似比.
结论:
你能有条理地表达理由吗?
那么
例2 如图,AF是△ABC的高,点D、E分别在AB、AC上,且DE ∥BC,DE交AF于点G .设DE=6,BC=10,GF=5,求点A到DE、BC的距离.
例题解析
解:由DE ∥BC, ∠AFB=90°,得
∠AGD=90 °,即AG ⊥DE.
于是,AG、AF的长分别为点A到DE、BC的距离.
在△ADE和△ABC中,
∵DE ∥BC,
∴ △ADE ∽ △ABC.
∴ (相似三角形对应线段的比等于相似比),
即
由此,得AG=7.5,AF=AG+5=12.5,
即点A到DE、BC的距离分别为7.5、12.5.
1、? 两个相似三角形的相似比为2 : 3,它们的对应角平分线之比为________,周长之比为_______,面积之比为_________.
2、若两个三角形面积之比为16:9,则它们的对高之比为_____,对应中线之比为_____.
3、如图, △ABC∽ △DBA,D为BC上一点,E、F分别是AC、AD的中点,且AB=28cm,BC=36cm,则BE:BF=________.
A
B
F
D
C
E
2 : 3
2 : 3
4 : 9
4 : 3
4 : 3
9 : 7
4.如图, △ ABC的面积为25,直线DE平行于BC分别交AB、AC于点D、E.如果△ ADE的面积为9,求 的值.
拓展练习
建颍乡建造一新住宅小区,同时在小区旁筑一条马路.在施工中遇到这样一个问题,小区旁原来有一个面积是64平方米,周长44米的三角形的荒地,由于建筑马路这块地被削去了一块梯形,原荒地的一边AB的长由原来的12米缩短成9米.然后在剩下的荒地上种绿化,你能不用工具测量,计算出现在绿化地面积到底有多大?它的周长是多少?
课后思考
有一块三角形铁片ABC,BC=12cm,高AH=8cm,按下(1)、(2)两种设计方案把它加工成一块矩形铁片DEFG,且要求矩形的长是宽的2倍,为了减少浪费,加工成的矩形铁片的面积应尽量大些.请你通过计算判断(1)、(2)两种设计方案哪个更好?
课后思考
小结:
性质1:相似三角形的周长比等于相似比;
性质2:相似三角形的面积比等于相似比的平方.
性质 3:相似三角形对应高的比等于相似比.
性质 4:相似三角形对应角平分线的比等于相似比.
性质 5:相似三角形对应中线的比等于相似比.
谢谢聆听
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
