6.6 图形的位似 课件(共29张PPT)
文档属性
| 名称 | 6.6 图形的位似 课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-19 18:14:38 | ||
图片预览


文档简介
6.6
图形的位似
第6章
图形的相似
2020-2021学年度苏科版九年级下册
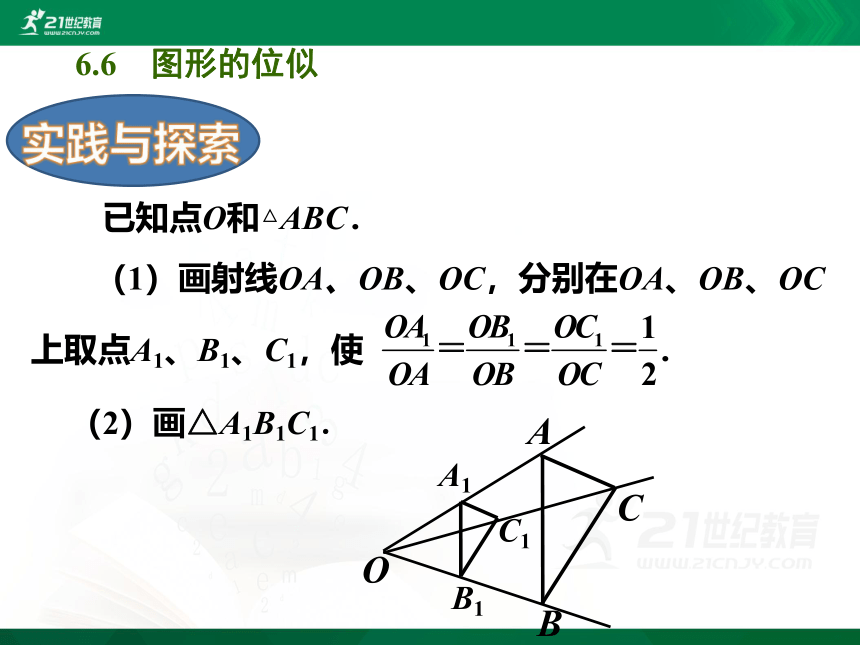
已知点O和△ABC.
(1)画射线OA、OB、OC,分别在OA、OB、OC
(2)画△A1B1C1.
上取点A1、B1、C1,使
.
A
B
C
O
A1
B1
C1
实践与探索
6.6 图形的位似
B
.
A
C
O
A2
B2
C2
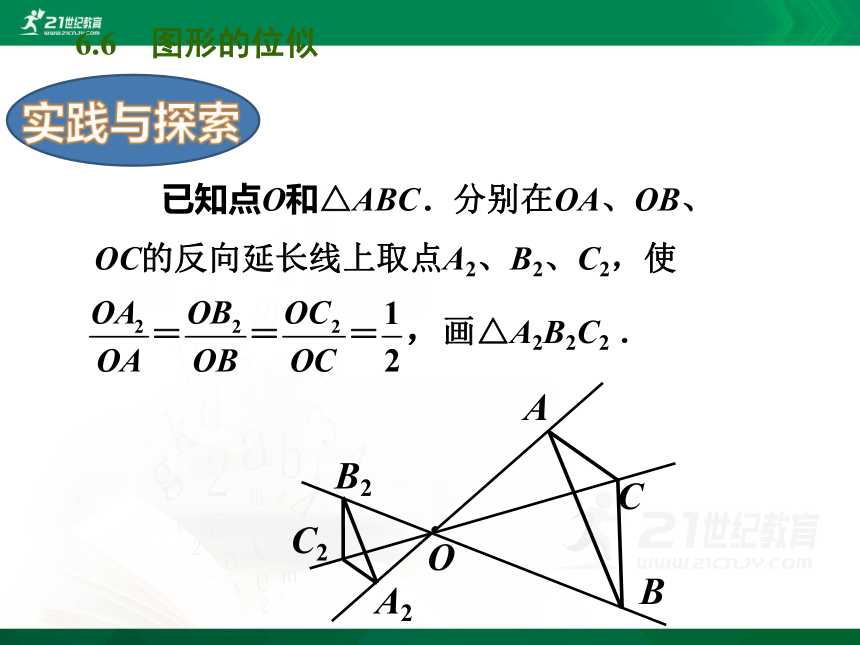
已知点O和△ABC.分别在OA、OB、OC的反向延长线上取点A2、B2、C2,使
,画△A2B2C2
.
实践与探索
6.6 图形的位似
A
B
A'
C'
B'
C
O
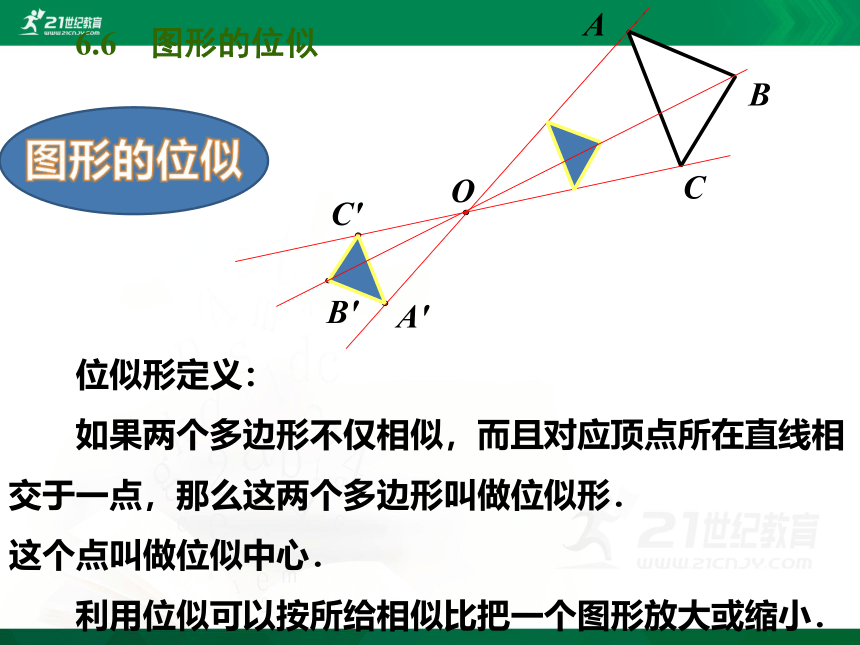
位似形定义:
如果两个多边形不仅相似,而且对应顶点所在直线相交于一点,那么这两个多边形叫做位似形.
这个点叫做位似中心.
利用位似可以按所给相似比把一个图形放大或缩小.
图形的位似
6.6 图形的位似
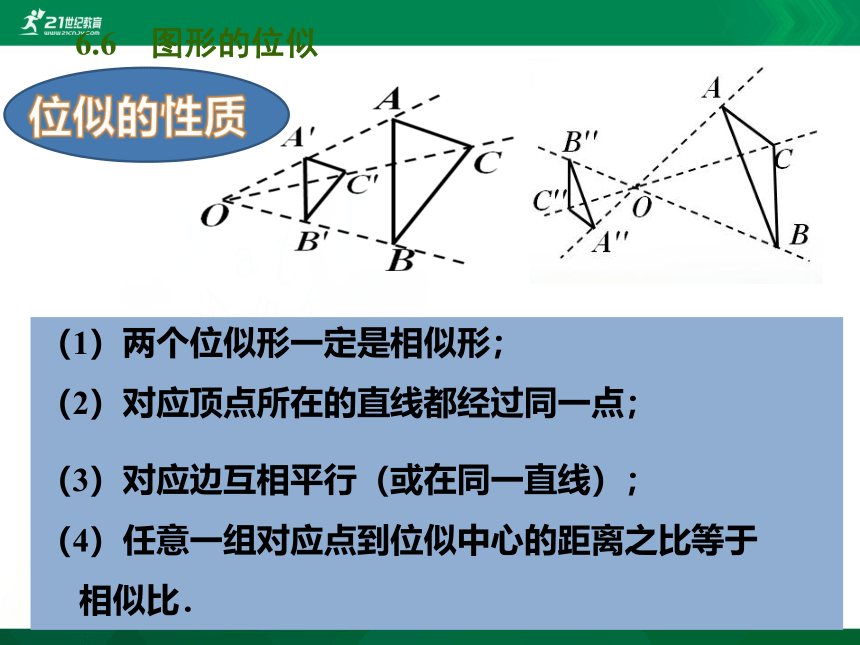
(1)两个位似形一定是相似形;
(2)对应顶点所在的直线都经过同一点;
(3)对应边互相平行(或在同一直线);
(4)任意一组对应点到位似中心的距离之比等于
相似比.
位似的性质
6.6 图形的位似
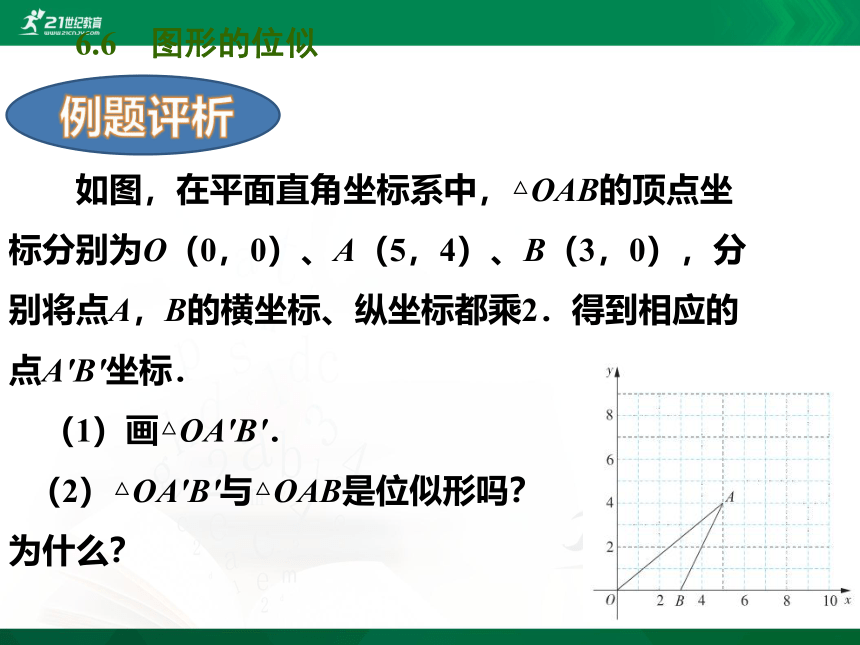
如图,在平面直角坐标系中,△OAB的顶点坐标分别为O(0,0)、A(5,4)、B(3,0),分别将点A,B的横坐标、纵坐标都乘2.得到相应的点A'B'坐标.
(1)画△OA'B'.
(2)△OA'B'与△OAB是位似形吗?
为什么?
例题评析
6.6 图形的位似
1.判断:
①位似图形一定是相似图形.( )
②相似图形一定是位似图形.( )
③位似图形中每组对应顶点所在直线相交于一点.( )
④位似图形中每组对应边所在直线必相互平行或在同一直线上.( )
⑤位似图形上对应顶点到位似中心的距离之比等于相似比.( )
随堂练习
6.6 图形的位似
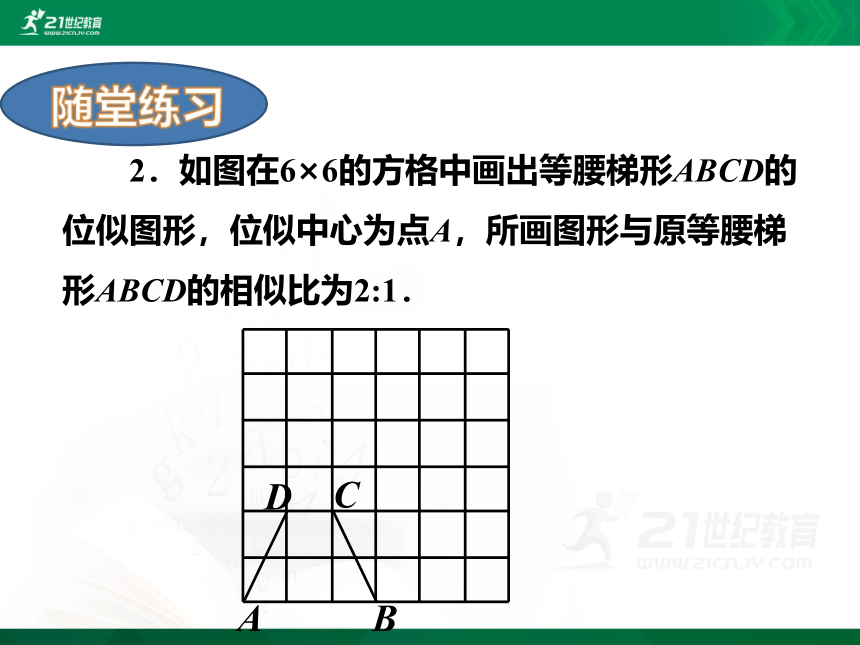
2.如图在6×6的方格中画出等腰梯形ABCD的位似图形,位似中心为点A,所画图形与原等腰梯形ABCD的相似比为2:1.
A
B
C
D
随堂练习
x
y
o
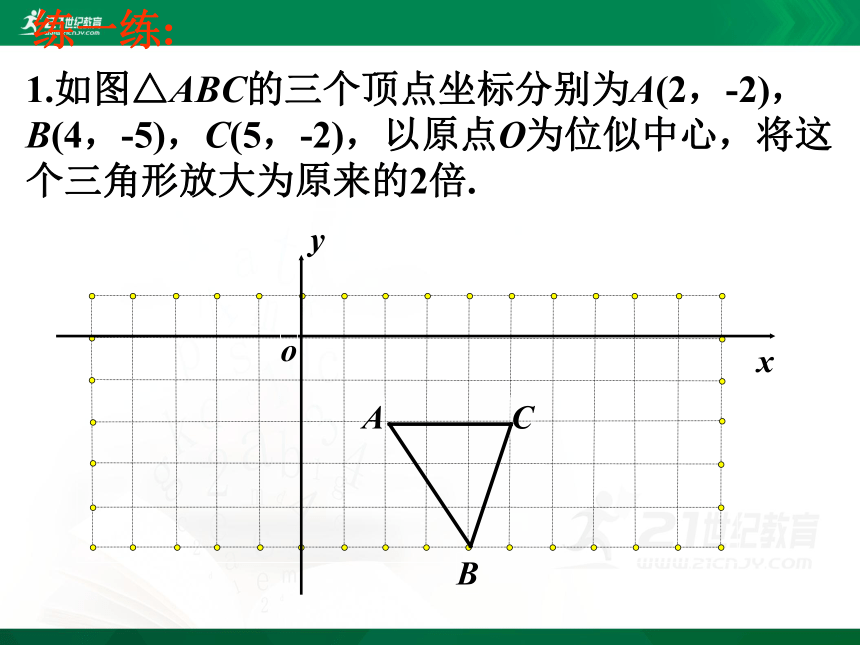
1.如图△ABC的三个顶点坐标分别为A(2,-2),B(4,-5),C(5,-2),以原点O为位似中心,将这个三角形放大为原来的2倍.
B
A
C
练一练:
x
y
o
2.在平面直角坐标系中,四边形ABCD的四个顶点的坐标分别为A(-6,6),B(-8,2),C(-4,0),D(-2,4),画出它的一个以原点O为位似中心,相似比为1/2的位似图形.
A′(
-3,3
),
B′(
-4,1
),
C′(
-2,0
),
D′(
-1,2
)
B
A
C
D
A′
B′
C′
D′
你还有其他办法吗?试试看.
1.如图表示△ABC把它缩小后得到的△COD,求它们的相似比.
x
y
o
B
A
C
D
大显身手
2.如图,写出矩形ABCD各点的坐标,如果矩形MNPQ∽矩形ABCD,点M的坐标为(2,2),按照下列相似比,分别写出M、P、Q各点的坐标.
x
y
o
A
B
C
D
(1)相似比为2;
(2)相似比为
;
大显身手
课外拓展
如图,在平面直角坐标系中,四边形ABCD四个顶点的坐标分别为A(-1,-1)、B(2,-1),C(2,2),D(-1,2).
(1)这个四边形是什么四边形?
(2)画出以O为位似中心,与四边形ABCD位似的图形A′B′
C′D′,使四边形ABCD各边长都放大为原来的2倍.
(3)写出位似图形中各点的坐标.
(4)各组对应点的坐标有何变化?
这样的放大缩小,没有改变图形形状,经过放大或缩小的图形,与原图形是相似的,因此,我们可以得到真实的图片和满意的照片.
在日常生活中,我们经常见到这样一类相似的图形,例如,放映幻灯时,通过光源,把幻灯片上的图形放大到屏幕上(如图显示了它工作的原理).
活动观察
图中有多边形相似吗?如果有,那么这种相似有什么特征?
观
察
图中每幅图中的两个多边形不仅相似,而且对应顶点的连线相交于一点,像这样的两个图形叫做位似图形,
O
O
O
这个点叫做位似中心.
已知点O和△ABC.
(1)画射线OA、OB、OC,分别在OA、OB、OC
(2)画△A1B1C1.
上取点A1、B1、C1,使
.
A
B
C
O
A1
B1
C1
课前探讨
B
.
A
C
O
A2
B2
C2
已知点O和△ABC.分别在OA、OB、OC的反向延长线上取点A2、B2、C2,使
,画△A2B2C2
.
课前探讨
A
B
A’
C’
B’
C
O
w
位似形定义:
如果两个多边形不仅相似,而且对应顶点所在直线相交于一点,那么这两个多边形叫做位似形.这个点叫做位似中心.
利用位似可以按所给相似比把一个图形放大或缩小.
图形位似
D
E
F
A
O
B
C
如何把三角形ABC放大为原来的2倍?
D
E
F
A
O
B
C
对应点连线都交于____________
对应线段_______________________________
位似中心
平行或在一条直线上
尝试与交流
(1)两个位似形一定是相似形;
(2)对应对应顶点所在的直线都经过同一点;
(3)对应边互相平行(或在同一直线);
(4)任一组对应点到位似中心的距之比等于相
似比.
位似图形的性质
如图,在平面直角坐标系中,△OAB的顶点坐标分别为O(0,0)、A(5,4)、B(3,0),分别将点A,B的横坐标、纵坐标都乘2.得到相应的点A'B'坐标.
实践与探索
(1)画△OA'B'.
(2)△OA'B'与△OAB是位似形吗?
为什么?
(2)已知矩形ABCD,AB=6,BC=4,试画出以点A为位
似中心与矩形ABCD位似的图形A′B′C′D′,使它的面
积等于矩形ABCD面积的1/4.
位似作图:
(1)如图,已知△ABC,请利用位似将△ABC各边长扩大
为原来的2倍.
位似比是多少?
1.如图表示△ABC把它缩小后得到的△COD,求它们的相似比.
x
y
O
B
A
C
D
大显身手
2.如图,写出矩形ABCD各点的坐标,如果矩形MNPQ∽矩形ABCD,点M的坐标为(2,2),按照下列相似比,分别写出M、P、Q各点的坐标.
x
y
O
A
B
C
D
(1)相似比为2;
(2)相似比为
;
大显身手
3.已知△ABC的三个顶点的坐标分别为(1,2),(-2,3),
(-1,0),把他们的横坐标和纵坐标都扩大到原来的2
倍,得到点A′,B′
,C′.
(1)作出△A′B′
C′.
(2)
△ABC与△
A′B′
C′是位似图形吗?如果是,位似中心是哪个点?位似比是多少?
x
y
O
A
B
C
-
2
2
2
4
6
(3)若将A、B、C三点的横坐标和
纵坐标分别都缩小为原来的一半,得到的三角形与△ABC是位似图形吗?若是,位似中心是哪个点?位似比是多少?
大显身手
4.如图,工人师傅为了在废旧三角形铁片上截取一个面积最大的正方形铁片,先用正方形模板在△ABC内画一个正方形,然后过正方形在三角形内的一个顶点画射线交边AC于点G,再作GF⊥BC,F为垂足,GD∥BC交AB于D,DE⊥BC,
E为垂足,则四边形DEFG就是最大的正方形这里用到了两个正方形位似的问题,它们的位似中心是_______.
A
B
C
G
F
D
E
大显身手
什么叫位似图形?
1
位似图形有哪些性质?
2
位似与平移、旋转等图形变换等有何不同点?
3
小结
每对对应点所在的直线都交于同一点的相似图形叫做位似图形.
如果两个位似图形的对应边平行或在同一条直线上,那么图形上任意一对对应点到位似中心的距离之比等于位似比
位似不仅改变了图形的位置,而且还可以改变图形的大小.
谢谢聆听
图形的位似
第6章
图形的相似
2020-2021学年度苏科版九年级下册
已知点O和△ABC.
(1)画射线OA、OB、OC,分别在OA、OB、OC
(2)画△A1B1C1.
上取点A1、B1、C1,使
.
A
B
C
O
A1
B1
C1
实践与探索
6.6 图形的位似
B
.
A
C
O
A2
B2
C2
已知点O和△ABC.分别在OA、OB、OC的反向延长线上取点A2、B2、C2,使
,画△A2B2C2
.
实践与探索
6.6 图形的位似
A
B
A'
C'
B'
C
O
位似形定义:
如果两个多边形不仅相似,而且对应顶点所在直线相交于一点,那么这两个多边形叫做位似形.
这个点叫做位似中心.
利用位似可以按所给相似比把一个图形放大或缩小.
图形的位似
6.6 图形的位似
(1)两个位似形一定是相似形;
(2)对应顶点所在的直线都经过同一点;
(3)对应边互相平行(或在同一直线);
(4)任意一组对应点到位似中心的距离之比等于
相似比.
位似的性质
6.6 图形的位似
如图,在平面直角坐标系中,△OAB的顶点坐标分别为O(0,0)、A(5,4)、B(3,0),分别将点A,B的横坐标、纵坐标都乘2.得到相应的点A'B'坐标.
(1)画△OA'B'.
(2)△OA'B'与△OAB是位似形吗?
为什么?
例题评析
6.6 图形的位似
1.判断:
①位似图形一定是相似图形.( )
②相似图形一定是位似图形.( )
③位似图形中每组对应顶点所在直线相交于一点.( )
④位似图形中每组对应边所在直线必相互平行或在同一直线上.( )
⑤位似图形上对应顶点到位似中心的距离之比等于相似比.( )
随堂练习
6.6 图形的位似
2.如图在6×6的方格中画出等腰梯形ABCD的位似图形,位似中心为点A,所画图形与原等腰梯形ABCD的相似比为2:1.
A
B
C
D
随堂练习
x
y
o
1.如图△ABC的三个顶点坐标分别为A(2,-2),B(4,-5),C(5,-2),以原点O为位似中心,将这个三角形放大为原来的2倍.
B
A
C
练一练:
x
y
o
2.在平面直角坐标系中,四边形ABCD的四个顶点的坐标分别为A(-6,6),B(-8,2),C(-4,0),D(-2,4),画出它的一个以原点O为位似中心,相似比为1/2的位似图形.
A′(
-3,3
),
B′(
-4,1
),
C′(
-2,0
),
D′(
-1,2
)
B
A
C
D
A′
B′
C′
D′
你还有其他办法吗?试试看.
1.如图表示△ABC把它缩小后得到的△COD,求它们的相似比.
x
y
o
B
A
C
D
大显身手
2.如图,写出矩形ABCD各点的坐标,如果矩形MNPQ∽矩形ABCD,点M的坐标为(2,2),按照下列相似比,分别写出M、P、Q各点的坐标.
x
y
o
A
B
C
D
(1)相似比为2;
(2)相似比为
;
大显身手
课外拓展
如图,在平面直角坐标系中,四边形ABCD四个顶点的坐标分别为A(-1,-1)、B(2,-1),C(2,2),D(-1,2).
(1)这个四边形是什么四边形?
(2)画出以O为位似中心,与四边形ABCD位似的图形A′B′
C′D′,使四边形ABCD各边长都放大为原来的2倍.
(3)写出位似图形中各点的坐标.
(4)各组对应点的坐标有何变化?
这样的放大缩小,没有改变图形形状,经过放大或缩小的图形,与原图形是相似的,因此,我们可以得到真实的图片和满意的照片.
在日常生活中,我们经常见到这样一类相似的图形,例如,放映幻灯时,通过光源,把幻灯片上的图形放大到屏幕上(如图显示了它工作的原理).
活动观察
图中有多边形相似吗?如果有,那么这种相似有什么特征?
观
察
图中每幅图中的两个多边形不仅相似,而且对应顶点的连线相交于一点,像这样的两个图形叫做位似图形,
O
O
O
这个点叫做位似中心.
已知点O和△ABC.
(1)画射线OA、OB、OC,分别在OA、OB、OC
(2)画△A1B1C1.
上取点A1、B1、C1,使
.
A
B
C
O
A1
B1
C1
课前探讨
B
.
A
C
O
A2
B2
C2
已知点O和△ABC.分别在OA、OB、OC的反向延长线上取点A2、B2、C2,使
,画△A2B2C2
.
课前探讨
A
B
A’
C’
B’
C
O
w
位似形定义:
如果两个多边形不仅相似,而且对应顶点所在直线相交于一点,那么这两个多边形叫做位似形.这个点叫做位似中心.
利用位似可以按所给相似比把一个图形放大或缩小.
图形位似
D
E
F
A
O
B
C
如何把三角形ABC放大为原来的2倍?
D
E
F
A
O
B
C
对应点连线都交于____________
对应线段_______________________________
位似中心
平行或在一条直线上
尝试与交流
(1)两个位似形一定是相似形;
(2)对应对应顶点所在的直线都经过同一点;
(3)对应边互相平行(或在同一直线);
(4)任一组对应点到位似中心的距之比等于相
似比.
位似图形的性质
如图,在平面直角坐标系中,△OAB的顶点坐标分别为O(0,0)、A(5,4)、B(3,0),分别将点A,B的横坐标、纵坐标都乘2.得到相应的点A'B'坐标.
实践与探索
(1)画△OA'B'.
(2)△OA'B'与△OAB是位似形吗?
为什么?
(2)已知矩形ABCD,AB=6,BC=4,试画出以点A为位
似中心与矩形ABCD位似的图形A′B′C′D′,使它的面
积等于矩形ABCD面积的1/4.
位似作图:
(1)如图,已知△ABC,请利用位似将△ABC各边长扩大
为原来的2倍.
位似比是多少?
1.如图表示△ABC把它缩小后得到的△COD,求它们的相似比.
x
y
O
B
A
C
D
大显身手
2.如图,写出矩形ABCD各点的坐标,如果矩形MNPQ∽矩形ABCD,点M的坐标为(2,2),按照下列相似比,分别写出M、P、Q各点的坐标.
x
y
O
A
B
C
D
(1)相似比为2;
(2)相似比为
;
大显身手
3.已知△ABC的三个顶点的坐标分别为(1,2),(-2,3),
(-1,0),把他们的横坐标和纵坐标都扩大到原来的2
倍,得到点A′,B′
,C′.
(1)作出△A′B′
C′.
(2)
△ABC与△
A′B′
C′是位似图形吗?如果是,位似中心是哪个点?位似比是多少?
x
y
O
A
B
C
-
2
2
2
4
6
(3)若将A、B、C三点的横坐标和
纵坐标分别都缩小为原来的一半,得到的三角形与△ABC是位似图形吗?若是,位似中心是哪个点?位似比是多少?
大显身手
4.如图,工人师傅为了在废旧三角形铁片上截取一个面积最大的正方形铁片,先用正方形模板在△ABC内画一个正方形,然后过正方形在三角形内的一个顶点画射线交边AC于点G,再作GF⊥BC,F为垂足,GD∥BC交AB于D,DE⊥BC,
E为垂足,则四边形DEFG就是最大的正方形这里用到了两个正方形位似的问题,它们的位似中心是_______.
A
B
C
G
F
D
E
大显身手
什么叫位似图形?
1
位似图形有哪些性质?
2
位似与平移、旋转等图形变换等有何不同点?
3
小结
每对对应点所在的直线都交于同一点的相似图形叫做位似图形.
如果两个位似图形的对应边平行或在同一条直线上,那么图形上任意一对对应点到位似中心的距离之比等于位似比
位似不仅改变了图形的位置,而且还可以改变图形的大小.
谢谢聆听
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
