2020-2021学年度 人教版七年级数学下册 5.2.2 平行线的判定 同步练习(Word版 含答案)
文档属性
| 名称 | 2020-2021学年度 人教版七年级数学下册 5.2.2 平行线的判定 同步练习(Word版 含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 136.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-19 00:00:00 | ||
图片预览

文档简介
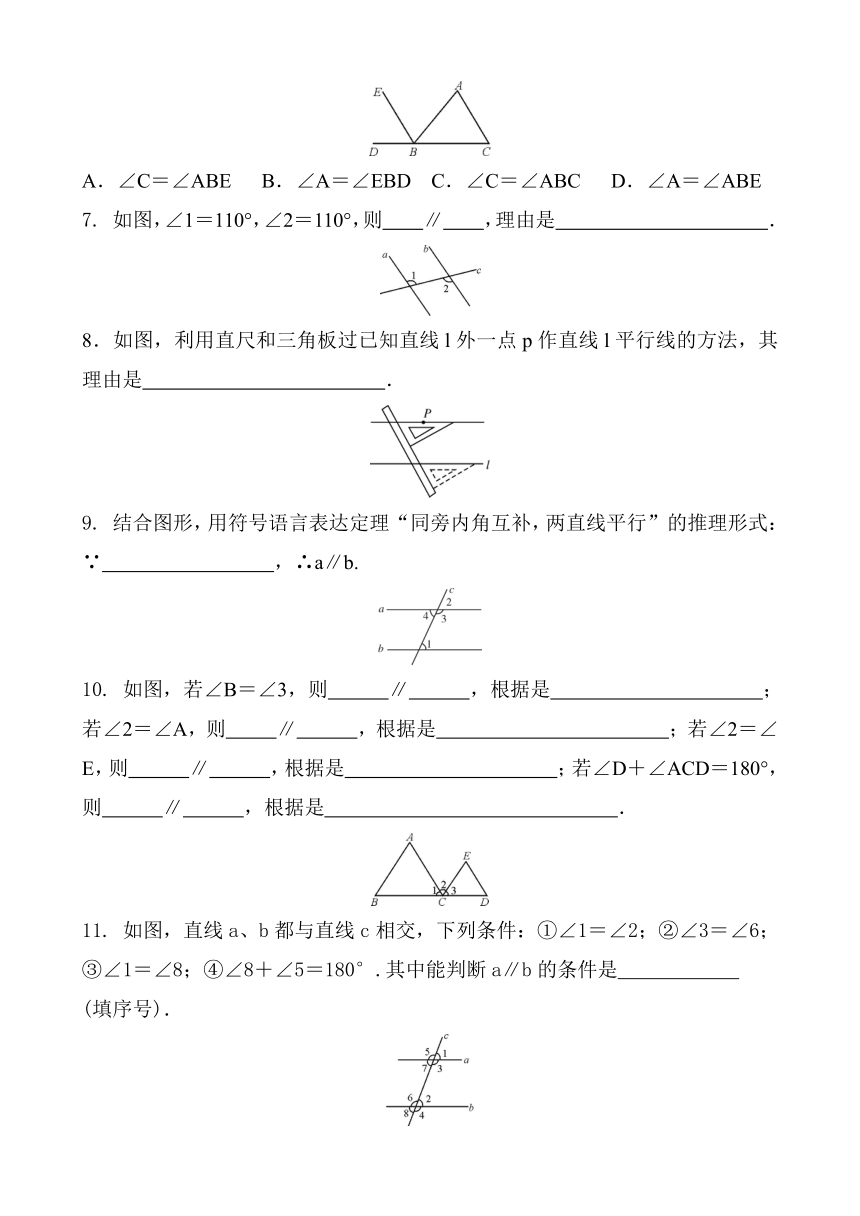
第五章 相交线与平行线 5.2.2 平行线的判定
1.如图,要使直线l∥OB,则∠1的度数是( )
A.120° B.30° C.40° D.60°
2. 如图,已知∠1=70°,要使AB∥CD,则须具备的另一条件是( )
A.∠2=70° B.∠2=100° C.∠2=110° D.∠3=110°
3. 如图,不能判定直线l1∥l2的是( )
A.∠1=∠3 B.∠2=∠3 C.∠4=∠5 D.∠2+∠4=180°
4. 如图,直线a、b被直线c所截,下列条件不能判定直线a与b平行的是( )
A.∠1=∠3 B.∠2+∠4=180° C.∠1=∠4 D.∠3=∠4
5. 如图,下列说法错误的是( )
A.若a∥b,b∥c,则a∥c B.若∠1=∠2,则a∥c
C.若∠3=∠2,则b∥c D.若∠3+∠5=180°,则a∥c
6. 如图,能判定EB∥AC的条件是( )
A.∠C=∠ABE B.∠A=∠EBD C.∠C=∠ABC D.∠A=∠ABE
7. 如图,∠1=110°,∠2=110°,则 ∥ ,理由是 .
8.如图,利用直尺和三角板过已知直线l外一点p作直线l平行线的方法,其理由是 .
9. 结合图形,用符号语言表达定理“同旁内角互补,两直线平行”的推理形式:∵ ,∴a∥b.
10. 如图,若∠B=∠3,则 ∥ ,根据是 ;若∠2=∠A,则 ∥ ,根据是 ;若∠2=∠E,则 ∥ ,根据是 ;若∠D+∠ACD=180°,则 ∥ ,根据是 .
11. 如图,直线a、b都与直线c相交,下列条件:①∠1=∠2;②∠3=∠6;③∠1=∠8;④∠8+∠5=180°.其中能判断a∥b的条件是
(填序号).
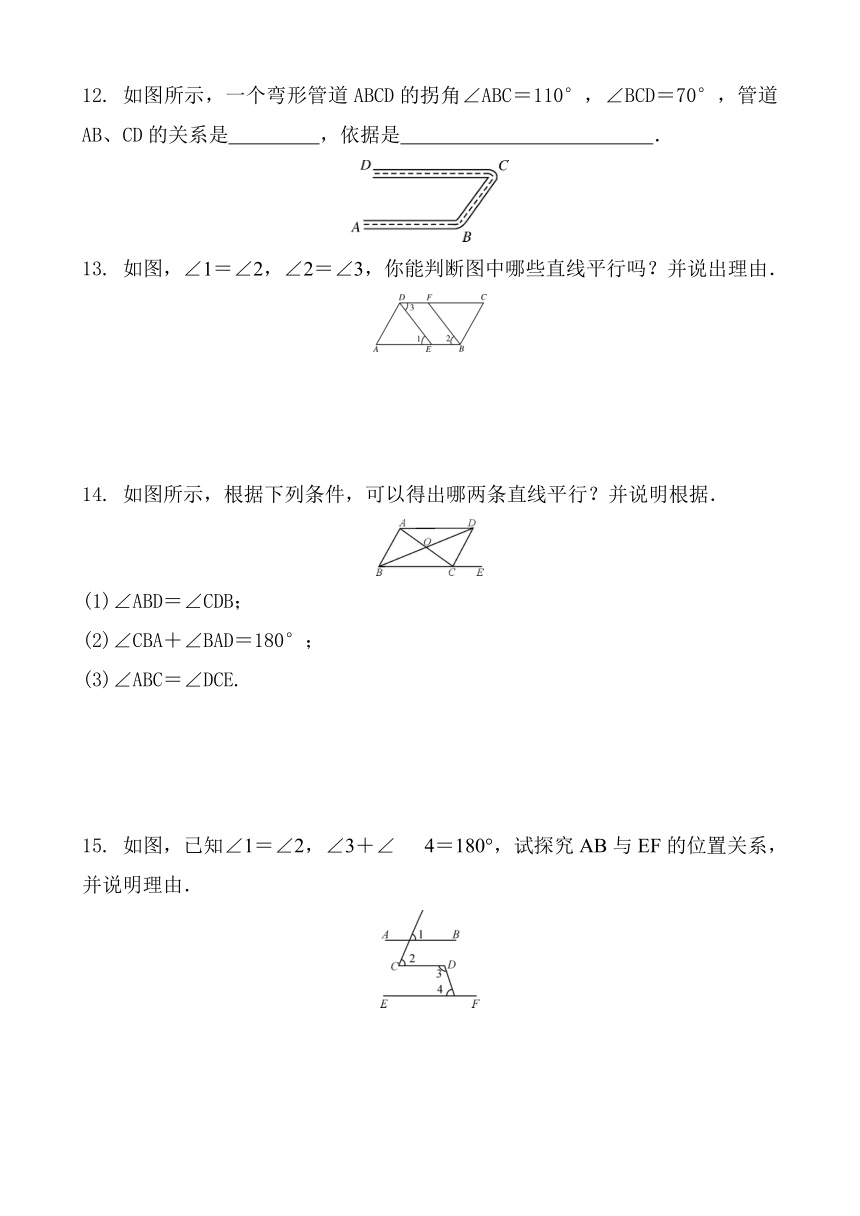
12. 如图所示,一个弯形管道ABCD的拐角∠ABC=110°,∠BCD=70°,管道AB、CD的关系是 ,依据是 .
13. 如图,∠1=∠2,∠2=∠3,你能判断图中哪些直线平行吗?并说出理由.
14. 如图所示,根据下列条件,可以得出哪两条直线平行?并说明根据.
(1)∠ABD=∠CDB;
(2)∠CBA+∠BAD=180°;
(3)∠ABC=∠DCE.
15. 如图,已知∠1=∠2,∠3+∠4=180°,试探究AB与EF的位置关系,并说明理由.
16. 如图,已知∠1=70°,∠CDN=125°,CM平分∠DCF.试判断CM与DN是否平行?并说明理由.
17. (1)如图①,若∠B+∠D=∠BED,试猜想AB与CD的位置关系并说明理由;
(2)如图②,要想得到AB∥CD,则∠1、∠2、∠3之间应满足怎样的关系呢?请探索.
答案:
1---5 DCBDD D
6. a b 内错角相等,两直线平行
7. 同位角相等,两直线平行
8. ∠1+∠3=180°
9. AB CE 同位角相等,两直线平行
AB CE 内错角相等,两直线平行
AC ED 内错角相等,两直线平行
AC ED 同旁内角互补,两直线平行
10. ① ② ③ ④
11. AB∥CD 同旁内角互补,两直线平行
12. 解:DE∥BF,AB∥CD.理由如下:∵∠1=∠2,∴DE∥BF(同位角相等,两直线平行).∵∠2=∠3,∴∠1=∠3(等量代换).∴AB∥CD(内错角相等,两直线平行).
13. (1)由∠ABD=∠CDB,可以得出AB∥CD,根据是“内错角相等,两直线平行”;
(2)由∠CBA+∠BAD=180°,可以得出AD∥BC,根据是“同旁内角互补,两直线平行”;
(3)由∠ABC=∠DCE,可以得出AB∥CD,根据是“同位角相等,两直线平行”.
14. 解:AB∥EF,理由:∵∠1=∠2,∴AB∥CD,又∵∠3+∠4=180°,∴CD∥EF,∴AB∥EF.
15. 解:CM∥DN.理由:∵∠1=70°,∴∠FCD=180°-70°=110°,∵CM平分∠FCD,∴∠MCD=55°,∵∠CDN=125°,∴∠MCD+∠CDN=180°,∴CM∥DN.
16. 解:(1)AB∥CD.理由:过点E在∠BED的内部作∠BEF=∠B,则AB∥EF.∵∠B+∠D=∠BED,∠BEF+∠DEF=∠BED,∴∠D=∠DEF,∴EF∥CD,∴AB∥CD;
(2)∠1=∠2+∠3.理由:过点E作∠AEM=∠1,则ME∥AB,∵∠1=∠2+∠3,∠AEM=∠2+∠MEC,∴∠3=∠MEC,∴ME∥CD,∴AB∥CD.
1.如图,要使直线l∥OB,则∠1的度数是( )
A.120° B.30° C.40° D.60°
2. 如图,已知∠1=70°,要使AB∥CD,则须具备的另一条件是( )
A.∠2=70° B.∠2=100° C.∠2=110° D.∠3=110°
3. 如图,不能判定直线l1∥l2的是( )
A.∠1=∠3 B.∠2=∠3 C.∠4=∠5 D.∠2+∠4=180°
4. 如图,直线a、b被直线c所截,下列条件不能判定直线a与b平行的是( )
A.∠1=∠3 B.∠2+∠4=180° C.∠1=∠4 D.∠3=∠4
5. 如图,下列说法错误的是( )
A.若a∥b,b∥c,则a∥c B.若∠1=∠2,则a∥c
C.若∠3=∠2,则b∥c D.若∠3+∠5=180°,则a∥c
6. 如图,能判定EB∥AC的条件是( )
A.∠C=∠ABE B.∠A=∠EBD C.∠C=∠ABC D.∠A=∠ABE
7. 如图,∠1=110°,∠2=110°,则 ∥ ,理由是 .
8.如图,利用直尺和三角板过已知直线l外一点p作直线l平行线的方法,其理由是 .
9. 结合图形,用符号语言表达定理“同旁内角互补,两直线平行”的推理形式:∵ ,∴a∥b.
10. 如图,若∠B=∠3,则 ∥ ,根据是 ;若∠2=∠A,则 ∥ ,根据是 ;若∠2=∠E,则 ∥ ,根据是 ;若∠D+∠ACD=180°,则 ∥ ,根据是 .
11. 如图,直线a、b都与直线c相交,下列条件:①∠1=∠2;②∠3=∠6;③∠1=∠8;④∠8+∠5=180°.其中能判断a∥b的条件是
(填序号).
12. 如图所示,一个弯形管道ABCD的拐角∠ABC=110°,∠BCD=70°,管道AB、CD的关系是 ,依据是 .
13. 如图,∠1=∠2,∠2=∠3,你能判断图中哪些直线平行吗?并说出理由.
14. 如图所示,根据下列条件,可以得出哪两条直线平行?并说明根据.
(1)∠ABD=∠CDB;
(2)∠CBA+∠BAD=180°;
(3)∠ABC=∠DCE.
15. 如图,已知∠1=∠2,∠3+∠4=180°,试探究AB与EF的位置关系,并说明理由.
16. 如图,已知∠1=70°,∠CDN=125°,CM平分∠DCF.试判断CM与DN是否平行?并说明理由.
17. (1)如图①,若∠B+∠D=∠BED,试猜想AB与CD的位置关系并说明理由;
(2)如图②,要想得到AB∥CD,则∠1、∠2、∠3之间应满足怎样的关系呢?请探索.
答案:
1---5 DCBDD D
6. a b 内错角相等,两直线平行
7. 同位角相等,两直线平行
8. ∠1+∠3=180°
9. AB CE 同位角相等,两直线平行
AB CE 内错角相等,两直线平行
AC ED 内错角相等,两直线平行
AC ED 同旁内角互补,两直线平行
10. ① ② ③ ④
11. AB∥CD 同旁内角互补,两直线平行
12. 解:DE∥BF,AB∥CD.理由如下:∵∠1=∠2,∴DE∥BF(同位角相等,两直线平行).∵∠2=∠3,∴∠1=∠3(等量代换).∴AB∥CD(内错角相等,两直线平行).
13. (1)由∠ABD=∠CDB,可以得出AB∥CD,根据是“内错角相等,两直线平行”;
(2)由∠CBA+∠BAD=180°,可以得出AD∥BC,根据是“同旁内角互补,两直线平行”;
(3)由∠ABC=∠DCE,可以得出AB∥CD,根据是“同位角相等,两直线平行”.
14. 解:AB∥EF,理由:∵∠1=∠2,∴AB∥CD,又∵∠3+∠4=180°,∴CD∥EF,∴AB∥EF.
15. 解:CM∥DN.理由:∵∠1=70°,∴∠FCD=180°-70°=110°,∵CM平分∠FCD,∴∠MCD=55°,∵∠CDN=125°,∴∠MCD+∠CDN=180°,∴CM∥DN.
16. 解:(1)AB∥CD.理由:过点E在∠BED的内部作∠BEF=∠B,则AB∥EF.∵∠B+∠D=∠BED,∠BEF+∠DEF=∠BED,∴∠D=∠DEF,∴EF∥CD,∴AB∥CD;
(2)∠1=∠2+∠3.理由:过点E作∠AEM=∠1,则ME∥AB,∵∠1=∠2+∠3,∠AEM=∠2+∠MEC,∴∠3=∠MEC,∴ME∥CD,∴AB∥CD.
