6.7 用相似三角形解决问题 课件(共31张PPT)
文档属性
| 名称 | 6.7 用相似三角形解决问题 课件(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-19 18:02:02 | ||
图片预览







文档简介
6.7 用相似三角形解决问题
第6章 图形的相似
2020-2021学年度苏科版九年级下册
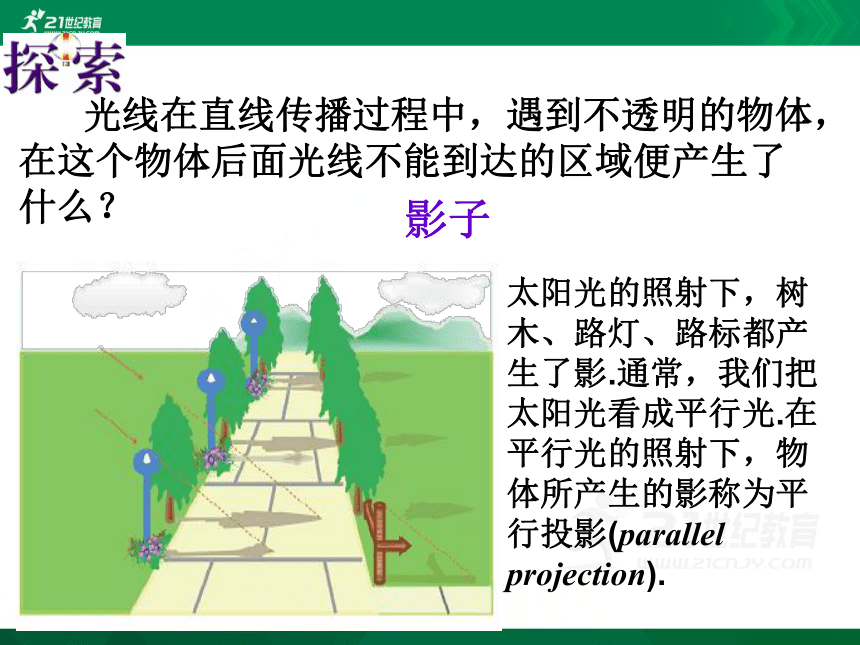
光线在直线传播过程中,遇到不透明的物体,在这个物体后面光线不能到达的区域便产生了什么?
影子
太阳光的照射下,树木、路灯、路标都产生了影.通常,我们把太阳光看成平行光.在平行光的照射下,物体所产生的影称为平行投影(parallel projection).
在学校操场上分别竖立长度不同的甲乙丙3根木杆,在同一时刻分别测量出3根木杆在阳光下的影长,并将有关数据填入下表:
木杆
木杆长度
杆影长度
木杆长度
杆影长度
甲
乙
丙
通过观察,你发现了什么?
2
3
1.5
2.25
2.2
3.3
木杆
木杆长度
杆影长度
杆影长度木杆长度
甲
乙
丙
2
3
1.5
1.5
2.25
1.5
2.2
3.3
1.5
2
3
1.5
2.25
2.2
3.3
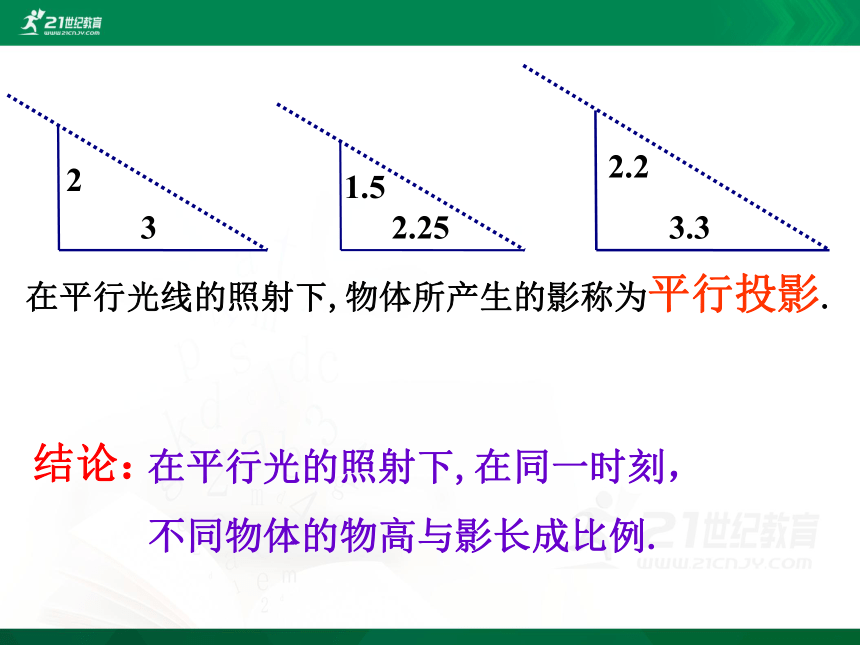
在平行光的照射下,在同一时刻,
不同物体的物高与影长成比例.
在平行光线的照射下,物体所产生的影称为平行投影.
结论:
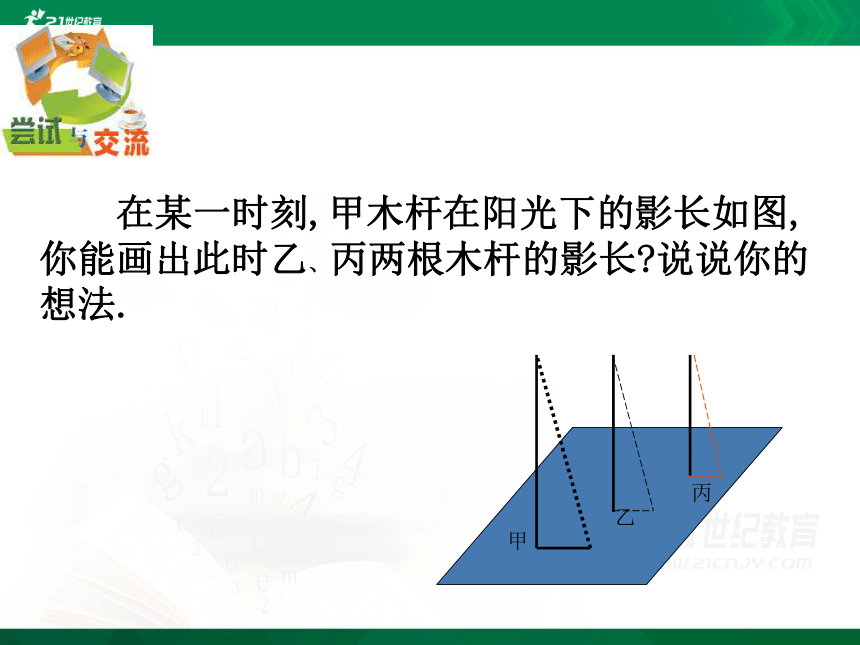
在某一时刻,甲木杆在阳光下的影长如图,你能画出此时乙、丙两根木杆的影长?说说你的想法.
甲
乙
丙
如图所示的测量旗杆的方法,已知AB是标杆,
BC表示AB在太阳光下的影子,叙述错误的是( )
A.可以利用在同一时刻,不同物体与其影长的
比相等来计算旗杆的高
B.可以利用△ABC∽△EDB,来计算旗杆的高
C.只需测量出标杆和旗杆
的影长就可计算出旗杆的高
D.需要测量出AB、BC和DB
的长,才能计算出旗杆的高
C
E
D
C
B
A
夜晚,当人在路灯下行走时,会看到一个有趣的现象:离开路灯越远,影子就越长.你能说说理由吗?请与同学交流.
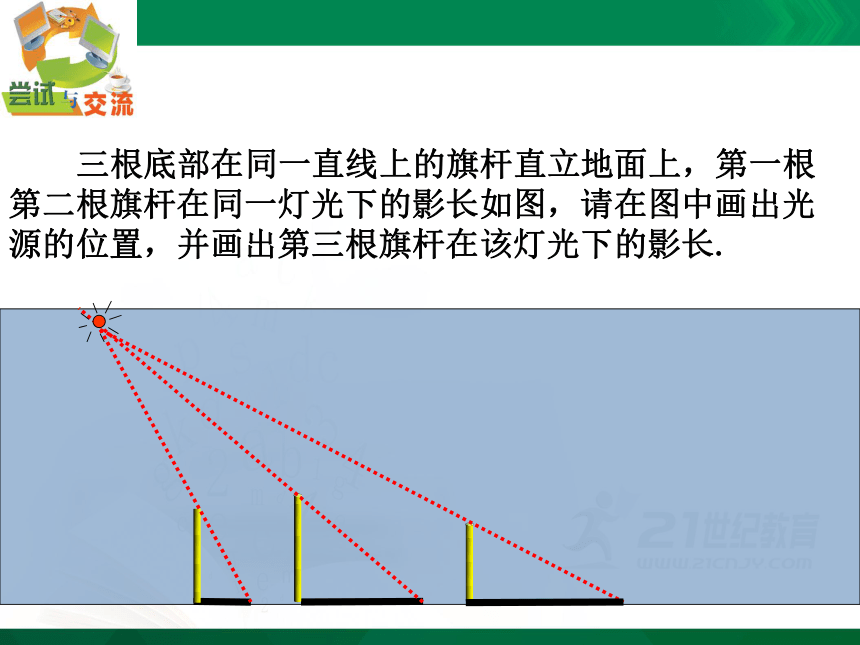
三根底部在同一直线上的旗杆直立地面上,第一根第二根旗杆在同一灯光下的影长如图,请在图中画出光源的位置,并画出第三根旗杆在该灯光下的影长.
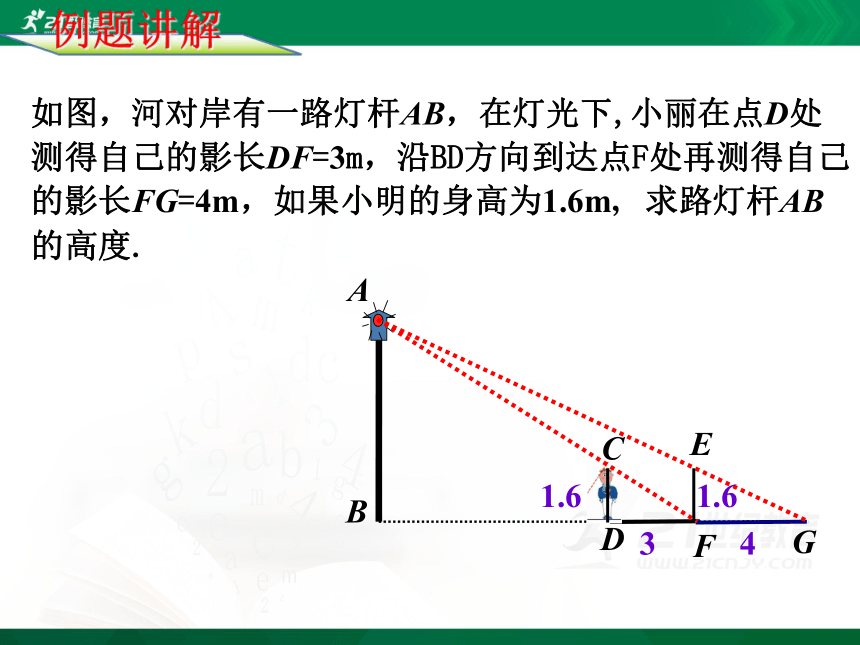
如图,河对岸有一路灯杆AB,在灯光下,小丽在点D处测得自己的影长DF=3m,沿BD方向到达点F处再测得自己的影长FG=4m,如果小明的身高为1.6m,求路灯杆AB的高度.
A
B
G
D
F
C
E
例题讲解
3
4
1.6
1.6
解:由AB ∥CD,得△ABF ∽ △CDF.
所以 ,即
①
由AB ∥EF,得△ABG ∽ △EFG.
所以 ,即
②
由①、 ②,得 ,BD=9.
将BD=9代入①,得 ,AB=6.4.
答:灯杆AB高6.4m.
在阳光下,身高1.68m的小强在地面上的影长为2m,在同一时刻,测得旗杆在地面上的影长为18m.求旗杆的高度(精确到0.1m).
如图,两棵树的高分别是AB=6m,CD=8m,两棵树的根部间的距离AC=4m.小明的眼睛与地面的距离为1.6m,当小明与树AB的距离小于多少时,就不能看到树CD的树顶D?
E
P
F
Q
B
A
D
C
G
H
1.已知为了测量路灯CD的高度,把一根长1.5m的竹竿AB竖直立在水平地面上.测得竹竿的影子长为1m,然后拿竹竿向远处路灯的方向走了4m.再把竹竿竖直立在地面上,竹竿的影长为1.8m,求路灯的高度.
变式练习
C
D
B
E
A'
B '
E '
A
2.如图,圆桌正上方的灯泡O(看成一个点)发出的光线照射到桌面后,在地面上形成影.设桌面的半径AC=0.8m,桌面与地面的距离AB=1m,灯泡与桌面的距离OA=2m,求地面上形成的影的面积.
变式练习
光线在直线传播过程中,遇到不透明的物体,在这个物体的后面光线不能到达的区域便产生影.
在平行光线的照射下,物体所产生的影称为平行投影.
在操场上,分别竖立长度不同的甲、乙、丙3根木杆,在同一时刻分别测量这3根木杆在阳光下的影长,并将有关数据填入下表:
通过观察、测量,
你发现了什么?请与同学交流.
在平行光线的照射下,不同物体的物高与影长成比例.
数学实验室
如图,甲木杆AB在阳光下的影长为BC.试在图中画出同一时刻乙、丙两根木杆在阳光下的影长.
尝试与交流
古埃及国王为了知道金字塔的高度,请一位学者来解决这个问题.在某一时刻,当这位学生确认阳光下他的影长等于他的身高时,要求他的助手测出金字塔的影长,这样他就十分准确地知道了金字塔的高度.
尝试与交流
例题:如图,AC是金字塔的高,如果此时测得金字塔的影DB的长为32m,金字塔底部正方形的边长为230m,你能计算这座金字塔的高度吗?
你能用这种方法测量出学校附近某一物体的高度吗?
1.身高为1.5m的小华在打高尔夫球,她在阳光下的影长为2.1m,此时她身后一棵水杉树的影长为10.5m,则这棵水杉树高为 ( ).
A.7.5m B.8m C.14.7m D.15.75m
练习与巩固
小丽利用影长测量学校旗杆的高度.由于旗杆靠近一个建筑物,在某一时刻旗杆影子中的一部分映在建筑物的墙上.小丽测得旗杆AB在地面上的影长BC为20m,在墙上的影长CD为4m,同时又测得竖立于地面的1m长的标杆影长为0.8m,请帮助小丽求出旗杆的高度.
拓展与延伸
夜晚,当人在路灯下行走时,会看到自己的影子有何变化?
路灯、台灯、手电筒的光可以看成是
从一个点发出的.如图,在点光源的照射下,
物体所产生的影称为中心投影.
思考:
在点光源的照射下,不同物体
的物高与影长成比例吗?
如图,河对岸有一灯杆AB,在灯光下,小丽在点D处测得自己的影长DF=3m,沿BD方向前进到达点F处测得自己的影长FG=4m.设小丽的身高为1.6m,求灯杆AB的高度.
例题讲解
解:由AB ∥CD,得△ABF ∽ △CDF.
所以 ,即
①
由AB ∥EF,得△ABG ∽ △EFG.
所以 ,即
②
由①、 ②,得 ,BD=9.
将BD=9代入①,得 ,AB=6.4.
答:灯杆AB高6.4m.
1.已知为了测量路灯CD的高度,把一根长1.5m的竹竿AB竖直立在水平地面上.测得竹竿的影子长为1m,然后拿竹竿向远处路灯的方向走了4m.再把竹竿竖直立在地面上,竹竿的影长为1.8m,求路灯的高度.
变式练习
C
D
B
E
A'
B '
E '
A
2.如图,圆桌正上方的灯泡O(看成一个点)发出的光线照射到桌面后,在地面上形成影.设桌面的半径AC=0.8m,桌面与地面的距离AB=1m,灯泡与桌面的距离OA=2m,求地面上形成的影的面积.
变式练习
谢谢聆听
第6章 图形的相似
2020-2021学年度苏科版九年级下册
光线在直线传播过程中,遇到不透明的物体,在这个物体后面光线不能到达的区域便产生了什么?
影子
太阳光的照射下,树木、路灯、路标都产生了影.通常,我们把太阳光看成平行光.在平行光的照射下,物体所产生的影称为平行投影(parallel projection).
在学校操场上分别竖立长度不同的甲乙丙3根木杆,在同一时刻分别测量出3根木杆在阳光下的影长,并将有关数据填入下表:
木杆
木杆长度
杆影长度
木杆长度
杆影长度
甲
乙
丙
通过观察,你发现了什么?
2
3
1.5
2.25
2.2
3.3
木杆
木杆长度
杆影长度
杆影长度木杆长度
甲
乙
丙
2
3
1.5
1.5
2.25
1.5
2.2
3.3
1.5
2
3
1.5
2.25
2.2
3.3
在平行光的照射下,在同一时刻,
不同物体的物高与影长成比例.
在平行光线的照射下,物体所产生的影称为平行投影.
结论:
在某一时刻,甲木杆在阳光下的影长如图,你能画出此时乙、丙两根木杆的影长?说说你的想法.
甲
乙
丙
如图所示的测量旗杆的方法,已知AB是标杆,
BC表示AB在太阳光下的影子,叙述错误的是( )
A.可以利用在同一时刻,不同物体与其影长的
比相等来计算旗杆的高
B.可以利用△ABC∽△EDB,来计算旗杆的高
C.只需测量出标杆和旗杆
的影长就可计算出旗杆的高
D.需要测量出AB、BC和DB
的长,才能计算出旗杆的高
C
E
D
C
B
A
夜晚,当人在路灯下行走时,会看到一个有趣的现象:离开路灯越远,影子就越长.你能说说理由吗?请与同学交流.
三根底部在同一直线上的旗杆直立地面上,第一根第二根旗杆在同一灯光下的影长如图,请在图中画出光源的位置,并画出第三根旗杆在该灯光下的影长.
如图,河对岸有一路灯杆AB,在灯光下,小丽在点D处测得自己的影长DF=3m,沿BD方向到达点F处再测得自己的影长FG=4m,如果小明的身高为1.6m,求路灯杆AB的高度.
A
B
G
D
F
C
E
例题讲解
3
4
1.6
1.6
解:由AB ∥CD,得△ABF ∽ △CDF.
所以 ,即
①
由AB ∥EF,得△ABG ∽ △EFG.
所以 ,即
②
由①、 ②,得 ,BD=9.
将BD=9代入①,得 ,AB=6.4.
答:灯杆AB高6.4m.
在阳光下,身高1.68m的小强在地面上的影长为2m,在同一时刻,测得旗杆在地面上的影长为18m.求旗杆的高度(精确到0.1m).
如图,两棵树的高分别是AB=6m,CD=8m,两棵树的根部间的距离AC=4m.小明的眼睛与地面的距离为1.6m,当小明与树AB的距离小于多少时,就不能看到树CD的树顶D?
E
P
F
Q
B
A
D
C
G
H
1.已知为了测量路灯CD的高度,把一根长1.5m的竹竿AB竖直立在水平地面上.测得竹竿的影子长为1m,然后拿竹竿向远处路灯的方向走了4m.再把竹竿竖直立在地面上,竹竿的影长为1.8m,求路灯的高度.
变式练习
C
D
B
E
A'
B '
E '
A
2.如图,圆桌正上方的灯泡O(看成一个点)发出的光线照射到桌面后,在地面上形成影.设桌面的半径AC=0.8m,桌面与地面的距离AB=1m,灯泡与桌面的距离OA=2m,求地面上形成的影的面积.
变式练习
光线在直线传播过程中,遇到不透明的物体,在这个物体的后面光线不能到达的区域便产生影.
在平行光线的照射下,物体所产生的影称为平行投影.
在操场上,分别竖立长度不同的甲、乙、丙3根木杆,在同一时刻分别测量这3根木杆在阳光下的影长,并将有关数据填入下表:
通过观察、测量,
你发现了什么?请与同学交流.
在平行光线的照射下,不同物体的物高与影长成比例.
数学实验室
如图,甲木杆AB在阳光下的影长为BC.试在图中画出同一时刻乙、丙两根木杆在阳光下的影长.
尝试与交流
古埃及国王为了知道金字塔的高度,请一位学者来解决这个问题.在某一时刻,当这位学生确认阳光下他的影长等于他的身高时,要求他的助手测出金字塔的影长,这样他就十分准确地知道了金字塔的高度.
尝试与交流
例题:如图,AC是金字塔的高,如果此时测得金字塔的影DB的长为32m,金字塔底部正方形的边长为230m,你能计算这座金字塔的高度吗?
你能用这种方法测量出学校附近某一物体的高度吗?
1.身高为1.5m的小华在打高尔夫球,她在阳光下的影长为2.1m,此时她身后一棵水杉树的影长为10.5m,则这棵水杉树高为 ( ).
A.7.5m B.8m C.14.7m D.15.75m
练习与巩固
小丽利用影长测量学校旗杆的高度.由于旗杆靠近一个建筑物,在某一时刻旗杆影子中的一部分映在建筑物的墙上.小丽测得旗杆AB在地面上的影长BC为20m,在墙上的影长CD为4m,同时又测得竖立于地面的1m长的标杆影长为0.8m,请帮助小丽求出旗杆的高度.
拓展与延伸
夜晚,当人在路灯下行走时,会看到自己的影子有何变化?
路灯、台灯、手电筒的光可以看成是
从一个点发出的.如图,在点光源的照射下,
物体所产生的影称为中心投影.
思考:
在点光源的照射下,不同物体
的物高与影长成比例吗?
如图,河对岸有一灯杆AB,在灯光下,小丽在点D处测得自己的影长DF=3m,沿BD方向前进到达点F处测得自己的影长FG=4m.设小丽的身高为1.6m,求灯杆AB的高度.
例题讲解
解:由AB ∥CD,得△ABF ∽ △CDF.
所以 ,即
①
由AB ∥EF,得△ABG ∽ △EFG.
所以 ,即
②
由①、 ②,得 ,BD=9.
将BD=9代入①,得 ,AB=6.4.
答:灯杆AB高6.4m.
1.已知为了测量路灯CD的高度,把一根长1.5m的竹竿AB竖直立在水平地面上.测得竹竿的影子长为1m,然后拿竹竿向远处路灯的方向走了4m.再把竹竿竖直立在地面上,竹竿的影长为1.8m,求路灯的高度.
变式练习
C
D
B
E
A'
B '
E '
A
2.如图,圆桌正上方的灯泡O(看成一个点)发出的光线照射到桌面后,在地面上形成影.设桌面的半径AC=0.8m,桌面与地面的距离AB=1m,灯泡与桌面的距离OA=2m,求地面上形成的影的面积.
变式练习
谢谢聆听
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
