7.2 正弦、余弦 课件(共29张PPT)
文档属性
| 名称 | 7.2 正弦、余弦 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-19 00:00:00 | ||
图片预览







文档简介
7.2 正弦、余弦
第7章 锐角三角函数
2020-2021学年度苏科版九年级下册
请你回忆:
1、锐角 A的正弦是如何定义的? 锐角A的余弦是如何定义的?
2、 30°、 45° 、 60°角的正余弦值各是多少?
3、sin A、cos A 是个比值,它与什么有关?
想一想
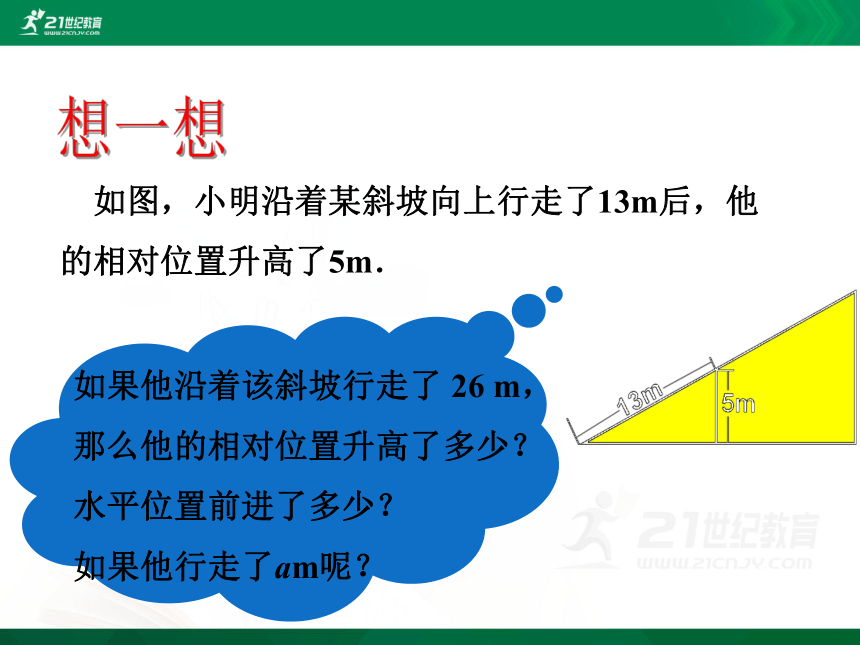
如图,小明沿着某斜坡向上行走了13m后,他的相对位置升高了5m.
如果他沿着该斜坡行走了 26 m,那么他的相对位置升高了多少?水平位置前进了多少?
如果他行走了am呢?
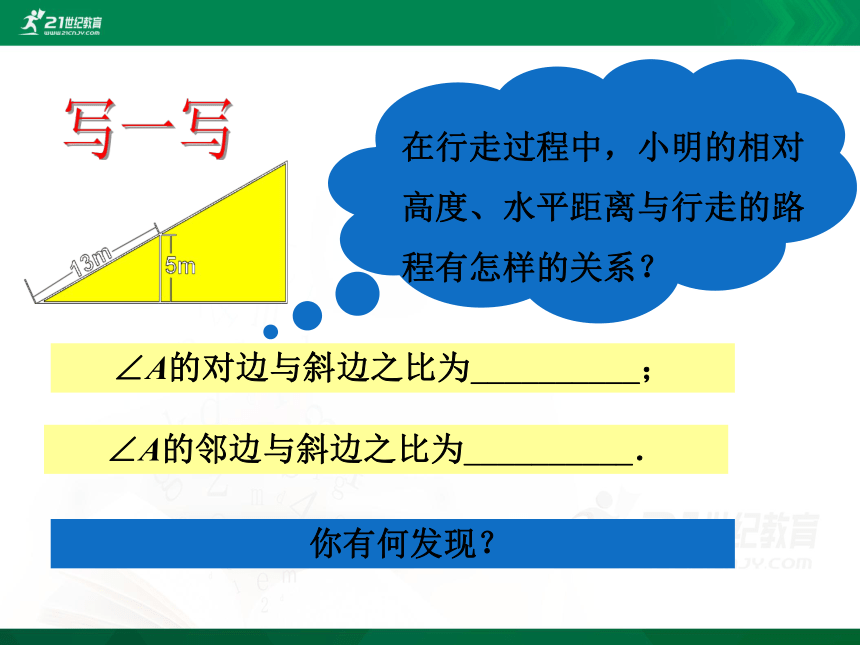
写一写
∠A的对边与斜边之比为__________;
∠A的邻边与斜边之比为__________.
你有何发现?
在行走过程中,小明的相对高度、水平距离与行走的路程有怎样的关系?
说一说
余弦:锐角∠A的邻边a与斜边c的比叫做∠A的余弦,记作cosA.
即:
正弦:锐角∠A的对边a与斜边c的比叫做∠A的正弦,记作sinA.
即:
sinA=
∠A的对边
斜边
=
a
c
cosA=
∠A的邻边
斜边
=
b
c
议一议
例1 如图,在等边三角形ABC中,求cos ∠B.
A
B
C
解:过点A做AD ⊥BC,垂足为D.
由题意知,BD= BC= AB.
在Rt △ABC中,
cos ∠B= .
1.在Rt△ABC中,∠C = 90° ,a=8 c=10 .求:cos A 和 sinB .
随堂练习
2.在Rt△ABC中,∠C=90°,a=2,b =1,求: ∠A的正弦和余弦,再写出∠B的正弦和余弦.
议一议
例2 利用计算器求下列各值(精确到0.01)
(1) sin75° ; (2)cos75°; (3)sin23?13′20′′.
解:
(1) sin75? =0.97;
(2)cos75?=0.25;
(3)sin23?13 ?20 ??=0.39.
借助计算器 ,求值(精确到0.01):
α
10°
20°
30°
40°
50?
60°
70°
80°
sinα
cosα
观察与发现
当锐角α越来越大时,
它的正弦值越来越_____,
它的余弦值越来越_____.
0.17
0.34
0.5
0.64
0.77
0.87
0.94
0.98
0.98
0.94
0.87
0.77
0.64
0.5
0.34
0.17
大
小
练一练
练一练
根据图形填空:
例3 如图,在Rt△ABC中,∠C=90°, AC=12,
BC=5.
求: sinA、cosA、sinB、cosB的值.
A
B
C
12
5
解:在Rt△ABC中,根据勾股定理,得
根据正弦、余弦的定义,得
例4 如图,在Rt△ABC中,∠C=90°,∠A=15 °,BC=6,求AB的长(精确到0.01).
解:由题意知,sinA= ,
则AB = .
用计算器计算,得AB≈23.18.
随堂练习
1.在△ABC中,∠C=90,AB=2,AC=1,则sinB的值
是______.
2.在Rt△ABC中,∠C=90°. AB=3AC.则
sinA=______,cosA=_____, tanA=______.
3.在△ABC中, ∠C=90°, 如果
求sinB,tanB的值.
用一用
小明从8m长的笔直滑梯自上而下滑至地面,已知滑梯的倾斜角为40°,求滑梯的高度(参考数据sin40°≈0.6428,cos40°≈ 0.7660,tan40°≈0.8391)(精确到0.1m).
A
B
C
tanA=
tanB=
练习:如图,△ABC的周长为36,且AB=AC=10,
求tanB.
复习回顾
A
B
C
D
要解决问题 2,就要利用本章将要学到的锐角三角函数的知识.
下面我们来探讨什么是锐角三角函数.
如图,是小明沿与地面成角 α 的山坡向上走了90米,如 果α=30,那么他上升了多少米?
如果α=60 °,那么他上升了多少米?
答:BC=45米.
A
C
B
对边
邻边
斜边
请大家在自己的草稿纸上画一个直角三角形,使其中一个锐角为65°,再请大家用直尺量一量65°角的对边和斜边的长,再算一算它们的比值,你把你的结果与你的同桌和周边其他同学比一比,想一想,你发现什么?(结果保留一位小数)
65°
5
4.5
探 究
由刚才分析可知:
当直角三角形的一个锐角的大小确定时,
它的对边与斜边的比值,邻边与斜边的比值也就确定.
A
B
C
在△ABC中,∠C=90°.
我们把锐角A的对边a与斜边c的比叫做
∠A的正弦,记作sinA.
A
B
C
我们把锐角A的邻边a与斜边c的比叫做
∠A的余弦,记作cosA.
sinA=
∠A的对边
斜边
=
a
c
∠A的邻边
斜边
=
b
c
cosA=
锐角A的正弦、余弦和正切都是∠A的三角函数.
典型例题
例1 如图,在等边三角形ABC中,求cos ∠B.
A
B
C
解:过点A做AD ⊥BC,垂足为D.
由题意知,BD= BC= AB.
在Rt△ABC中,
cos ∠B= .
如何用量角器与刻度尺求出sin15°、
及cos15°的值?
15?
A
C
B
1)画∠A=15°,在∠A一边上取一点B作BC垂直于另一边,垂足为C.
2)测量BC与AB的长度,求出BC与AB的比值.
思考:
注:为了方便,通过我们可取AB=1.
典型例题
例2 利用计算器求下列各值(精确到0.01)
(1)sin75°; (2)cos75°; (3)sin23°13′20″.
解:
(1) sin75° =0.97;
(2)cos75° =0.25;
(3)sin23°13′20″=0.39.
例3 如图,在Rt△ABC中,∠C=90°,AC=12,
BC=5.
求: sinA、cosA、sinB、cosB的值.
A
B
C
12
5
解:在Rt△ABC中,根据勾股定理,得
根据正弦、余弦的定义,得
例4如图,在Rt△ABC中,∠C=90°,∠A=15°,BC=6,求AB的长(精确到0.01).
解:由题意知,sinA= ,
则AB = .
用计算器计算,得AB≈23.18.
练习
1、如图,在Rt△ABC中,∠C=90°, BC=5,AB=13.
(1)求sinA、 sinB的值;
(2)求cosB的值.
A
C
B
13
5
2、某中学有一块三角形形状的花圃ABC,如图,现可直接测量到∠A=30°,AC=40m,BC=25m,请你求出这块花圃的面积(结果保留根号).(锐角的正弦表示直角三角形的边角关系,必要时可作高.)
C
B
A
课堂小结
三
角
函
数
正弦
余弦
正切
sinA=
∠A的对边
斜边
=
a
c
∠A的邻边
斜边
=
b
c
cosA=
∠A的对边
∠A的邻边
=
b
a
tanA=
谢谢聆听
第7章 锐角三角函数
2020-2021学年度苏科版九年级下册
请你回忆:
1、锐角 A的正弦是如何定义的? 锐角A的余弦是如何定义的?
2、 30°、 45° 、 60°角的正余弦值各是多少?
3、sin A、cos A 是个比值,它与什么有关?
想一想
如图,小明沿着某斜坡向上行走了13m后,他的相对位置升高了5m.
如果他沿着该斜坡行走了 26 m,那么他的相对位置升高了多少?水平位置前进了多少?
如果他行走了am呢?
写一写
∠A的对边与斜边之比为__________;
∠A的邻边与斜边之比为__________.
你有何发现?
在行走过程中,小明的相对高度、水平距离与行走的路程有怎样的关系?
说一说
余弦:锐角∠A的邻边a与斜边c的比叫做∠A的余弦,记作cosA.
即:
正弦:锐角∠A的对边a与斜边c的比叫做∠A的正弦,记作sinA.
即:
sinA=
∠A的对边
斜边
=
a
c
cosA=
∠A的邻边
斜边
=
b
c
议一议
例1 如图,在等边三角形ABC中,求cos ∠B.
A
B
C
解:过点A做AD ⊥BC,垂足为D.
由题意知,BD= BC= AB.
在Rt △ABC中,
cos ∠B= .
1.在Rt△ABC中,∠C = 90° ,a=8 c=10 .求:cos A 和 sinB .
随堂练习
2.在Rt△ABC中,∠C=90°,a=2,b =1,求: ∠A的正弦和余弦,再写出∠B的正弦和余弦.
议一议
例2 利用计算器求下列各值(精确到0.01)
(1) sin75° ; (2)cos75°; (3)sin23?13′20′′.
解:
(1) sin75? =0.97;
(2)cos75?=0.25;
(3)sin23?13 ?20 ??=0.39.
借助计算器 ,求值(精确到0.01):
α
10°
20°
30°
40°
50?
60°
70°
80°
sinα
cosα
观察与发现
当锐角α越来越大时,
它的正弦值越来越_____,
它的余弦值越来越_____.
0.17
0.34
0.5
0.64
0.77
0.87
0.94
0.98
0.98
0.94
0.87
0.77
0.64
0.5
0.34
0.17
大
小
练一练
练一练
根据图形填空:
例3 如图,在Rt△ABC中,∠C=90°, AC=12,
BC=5.
求: sinA、cosA、sinB、cosB的值.
A
B
C
12
5
解:在Rt△ABC中,根据勾股定理,得
根据正弦、余弦的定义,得
例4 如图,在Rt△ABC中,∠C=90°,∠A=15 °,BC=6,求AB的长(精确到0.01).
解:由题意知,sinA= ,
则AB = .
用计算器计算,得AB≈23.18.
随堂练习
1.在△ABC中,∠C=90,AB=2,AC=1,则sinB的值
是______.
2.在Rt△ABC中,∠C=90°. AB=3AC.则
sinA=______,cosA=_____, tanA=______.
3.在△ABC中, ∠C=90°, 如果
求sinB,tanB的值.
用一用
小明从8m长的笔直滑梯自上而下滑至地面,已知滑梯的倾斜角为40°,求滑梯的高度(参考数据sin40°≈0.6428,cos40°≈ 0.7660,tan40°≈0.8391)(精确到0.1m).
A
B
C
tanA=
tanB=
练习:如图,△ABC的周长为36,且AB=AC=10,
求tanB.
复习回顾
A
B
C
D
要解决问题 2,就要利用本章将要学到的锐角三角函数的知识.
下面我们来探讨什么是锐角三角函数.
如图,是小明沿与地面成角 α 的山坡向上走了90米,如 果α=30,那么他上升了多少米?
如果α=60 °,那么他上升了多少米?
答:BC=45米.
A
C
B
对边
邻边
斜边
请大家在自己的草稿纸上画一个直角三角形,使其中一个锐角为65°,再请大家用直尺量一量65°角的对边和斜边的长,再算一算它们的比值,你把你的结果与你的同桌和周边其他同学比一比,想一想,你发现什么?(结果保留一位小数)
65°
5
4.5
探 究
由刚才分析可知:
当直角三角形的一个锐角的大小确定时,
它的对边与斜边的比值,邻边与斜边的比值也就确定.
A
B
C
在△ABC中,∠C=90°.
我们把锐角A的对边a与斜边c的比叫做
∠A的正弦,记作sinA.
A
B
C
我们把锐角A的邻边a与斜边c的比叫做
∠A的余弦,记作cosA.
sinA=
∠A的对边
斜边
=
a
c
∠A的邻边
斜边
=
b
c
cosA=
锐角A的正弦、余弦和正切都是∠A的三角函数.
典型例题
例1 如图,在等边三角形ABC中,求cos ∠B.
A
B
C
解:过点A做AD ⊥BC,垂足为D.
由题意知,BD= BC= AB.
在Rt△ABC中,
cos ∠B= .
如何用量角器与刻度尺求出sin15°、
及cos15°的值?
15?
A
C
B
1)画∠A=15°,在∠A一边上取一点B作BC垂直于另一边,垂足为C.
2)测量BC与AB的长度,求出BC与AB的比值.
思考:
注:为了方便,通过我们可取AB=1.
典型例题
例2 利用计算器求下列各值(精确到0.01)
(1)sin75°; (2)cos75°; (3)sin23°13′20″.
解:
(1) sin75° =0.97;
(2)cos75° =0.25;
(3)sin23°13′20″=0.39.
例3 如图,在Rt△ABC中,∠C=90°,AC=12,
BC=5.
求: sinA、cosA、sinB、cosB的值.
A
B
C
12
5
解:在Rt△ABC中,根据勾股定理,得
根据正弦、余弦的定义,得
例4如图,在Rt△ABC中,∠C=90°,∠A=15°,BC=6,求AB的长(精确到0.01).
解:由题意知,sinA= ,
则AB = .
用计算器计算,得AB≈23.18.
练习
1、如图,在Rt△ABC中,∠C=90°, BC=5,AB=13.
(1)求sinA、 sinB的值;
(2)求cosB的值.
A
C
B
13
5
2、某中学有一块三角形形状的花圃ABC,如图,现可直接测量到∠A=30°,AC=40m,BC=25m,请你求出这块花圃的面积(结果保留根号).(锐角的正弦表示直角三角形的边角关系,必要时可作高.)
C
B
A
课堂小结
三
角
函
数
正弦
余弦
正切
sinA=
∠A的对边
斜边
=
a
c
∠A的邻边
斜边
=
b
c
cosA=
∠A的对边
∠A的邻边
=
b
a
tanA=
谢谢聆听
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
