人教版初中数学 八年下册 第十八章 平行四边形 章节训练(word含答案)
文档属性
| 名称 | 人教版初中数学 八年下册 第十八章 平行四边形 章节训练(word含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 406.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-19 19:15:29 | ||
图片预览



文档简介
人教版初中数学
八年下册
第十八章
平行四边形
章节训练
一、选择题
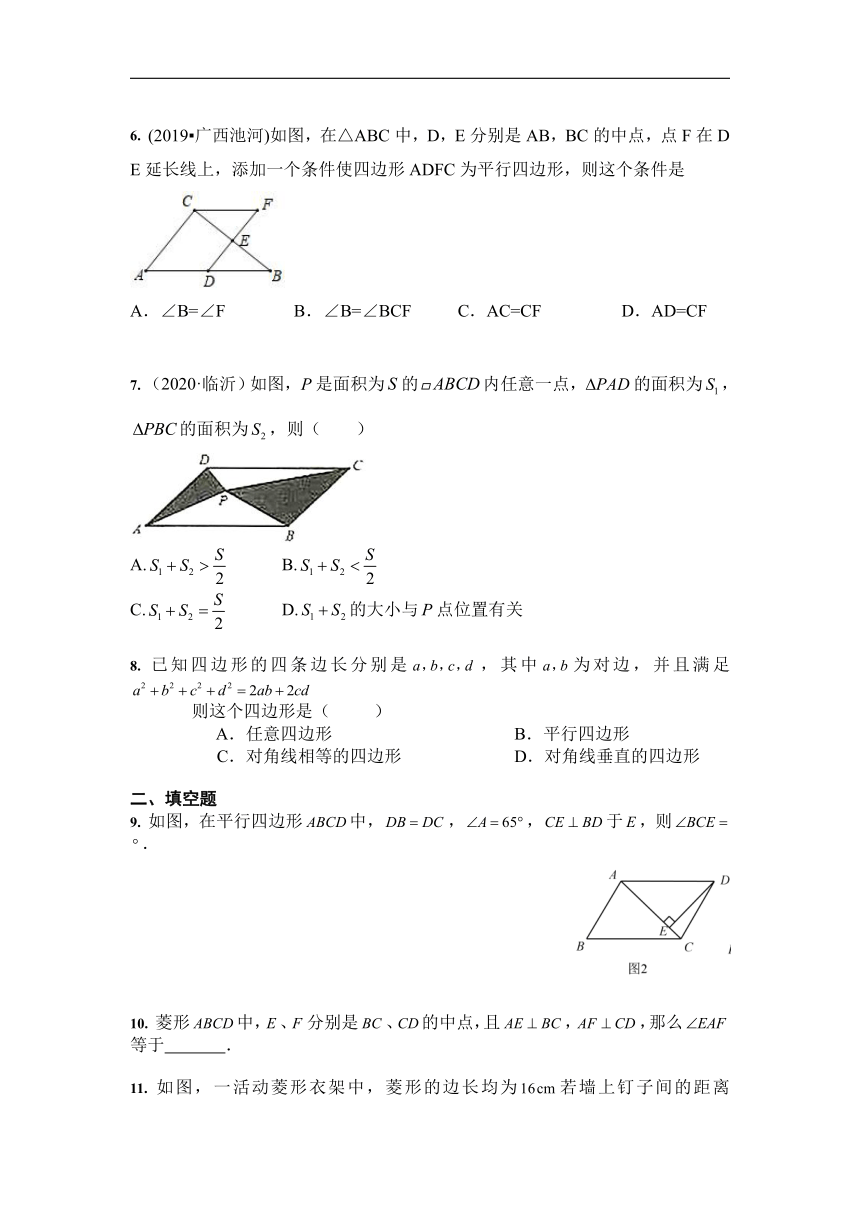
1.
如图,在?ABCD中,BM是∠ABC的平分线交CD于点M,且MC=2,?ABCD的周长是14,则DM等于( )
A.
1 B.
2 C.
3 D.
4
2.
以三角形的三个顶点作平行四边形,最多可以作(
)
A.2个
B.3个
C.4个
D.5个
3.
(2020·荆门)如图,菱形ABCD中,E,F分别是AD,BD的中点,若EF=5,则菱形ABCD的周长为(
)
A.20
B.30
C.40
D.50
(
D
A
C
B
F
E
)
4.
(2020·通辽)如图,AD是△ABC的中线,四边形ADCE是平行四边形,增加下列条件,能判断?ADCE是菱形的是( )
A.∠BAC=90°
B.∠DAE=90°
C.AB=AC
D.AB=AE
5.
如图,把一张矩形纸片ABCD沿对角线AC折叠,点B的对应点为B′,AB′与DC相交于点E,则下列结论一定正确的是( )
A.∠DAB′=∠CAB′
B.∠ACD=∠B′CD
C.AD=AE
D.AE=CE
6.
(2019?广西池河)如图,在△ABC中,D,E分别是AB,BC的中点,点F在DE延长线上,添加一个条件使四边形ADFC为平行四边形,则这个条件是
A.∠B=∠F
B.∠B=∠BCF
C.AC=CF
D.AD=CF
7.
(2020·临沂)如图,是面积为的内任意一点,的面积为,的面积为,则(
)
A.
B.
C.
D.的大小与点位置有关
8.
已知四边形的四条边长分别是,其中为对边,并且满足
则这个四边形是(
)
A.任意四边形
B.平行四边形
C.对角线相等的四边形
D.对角线垂直的四边形
二、填空题
9.
如图,在平行四边形中,,,于,则
.
10.
菱形中,、分别是、的中点,且,,那么等于
.
11.
如图,一活动菱形衣架中,菱形的边长均为若墙上钉子间的距离,则
度.
12.
已知正方形的边长是正方形的对角线,则
13.
如图所示,四边形ABCD的对角线相交于点O,若AB∥CD,请添加一个条件________(写一个即可),使四边形ABCD是平行四边形.
14.
如图,在ABCD中,E.F是对角线AC上两点,AE=EF=CD,∠ADF=90°,∠BCD=63°,则∠ADE的大小为__________.
15.
某台球桌为如图所示长方形,小球从沿角出击,恰好经过次碰撞到处,则=
16.
如图,正方形ABCD的面积为3
cm2,E为BC边上一点,∠BAE=30°,F为AE的中点,过点F作直线分别与AB,DC相交于点M,N.若MN=AE,则AM的长等于________cm.
三、解答题
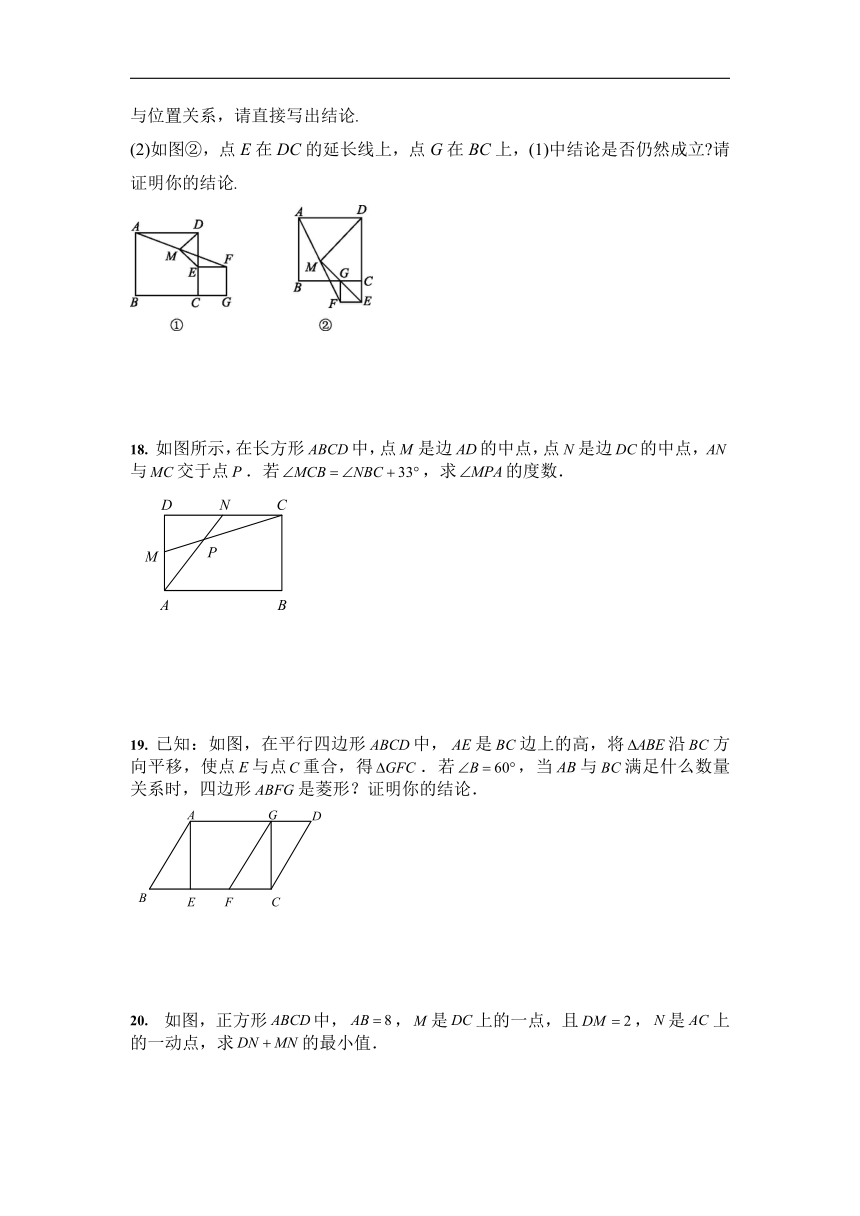
17.
如图,已知正方形ABCD与正方形CEFG,M是AF的中点,连接DM,EM.
(1)如图①,点E在CD上,点G在BC的延长线上,判断DM,EM的数量关系与位置关系,请直接写出结论.
(2)如图②,点E在DC的延长线上,点G在BC上,(1)中结论是否仍然成立?请证明你的结论.
18.
如图所示,在长方形中,点是边的中点,点是边的中点,与交于点.若,求的度数.
19.
已知:如图,在平行四边形中,是边上的高,将沿方向平移,使点与点重合,得.若,当与满足什么数量关系时,四边形是菱形?证明你的结论.
20.
如图,正方形中,,是上的一点,且,是上的一动点,求的最小值.
人教版初中数学
八年下册
第十八章
平行四边形
章节训练-答案
一、选择题
1.
【答案】C 【解析】∵四边形ABCD是平行四边形,∴AB∥CD,∴∠ABM=∠CMB,∵BM平分∠ABC,∴∠ABM=∠CBM,∴∠CBM=∠CMB,∴CB=MC=2,∴AD=BC=2,∵?ABCD的周长是14,∴AB=CD=5,∴DM=DC-MC=3.
2.
【答案】B
3.
【答案】C
【解析】∵E,F分别是AD,BD的中点,∴EF是△DAB的中位线.∴AB=2EF=10.∵菱形的四边相等,∴菱形ABCD的周长=4AB=40.故选C.
4.
【答案】A
【解析】若∠BAC=90°,又因为AD是△ABC的中线,根据“直角三角形斜边上的中线等于斜边的一半”可得AD=CD,根据“有一组邻边相等的平行四边形是菱形”可证?ADCE是菱形.
5.
【答案】D 【解析】∵四边形ABCD为矩形,∴AB∥CD,∴∠ACD=∠BAC,由折叠的性质可得∠BAC
=∠EAC,
∴∠ACD=∠EAC,∴AE=CE.
6.
【答案】B
【解析】∵在△ABC中,D,E分别是AB,BC的中点,
∴DE是△ABC的中位线,∴DEAC.
A.根据∠B=∠F不能判定AC∥DF,即不能判定四边形ADFC为平行四边形,故本选项错误.
B.根据∠B=∠BCF可以判定CF∥AB,即CF∥AD,由“两组对边分别平行的四边形是平行四边形”得到四边形ADFC为平行四边形,故本选项正确.
C.根据AC=CF不能判定AC∥DF,即不能判定四边形ADFC为平行四边形,故本选项错误.
D.根据AD=CF,FD∥AC不能判定四边形ADFC为平行四边形,故本选项错误.
故选B.
7.
【答案】C
【解析】可以利用割补法对平行四边形进行分割,然后使分割后的图形与的面积,的面积发生关联,然后求出其数量关系,如下图,过点P作AD的平行线,分别交的边于点M、N:
.
8.
【答案】B
二、填空题
9.
【答案】
【解析】∵四边形是平行四边形
∴
又∵
∴,∴
又∵,∴
∴.
10.
【答案】
11.
【答案】
【解析】由题意可知:构成三角形为等边三角形
12.
【答案】
13.
【答案】AD∥BC(答案不唯一) 【解析】根据平行四边形的判定,在已有AB∥DC的条件下,可再加另一组对边平行即可证得它是平行四边形,即加“AD∥BC”.
14.
【答案】21°
【解析】设∠ADE=x,
∵AE=EF,∠ADF=90°,
∴∠DAE=∠ADE=x,DE=AF=AE=EF,
∵AE=EF=CD,∴DE=CD,
∴∠DCE=∠DEC=2x,
∵四边形ABCD是平行四边形,∴AD∥BC,
∴∠DAE=∠BCA=x,
∴∠DCE=∠BCD﹣∠BCA=63°﹣x,
∴2x=63°﹣x,解得x=21°,即∠ADE=21°;
故答案为:21°.
15.
【答案】
【解析】由图形可知:可推出
16.
【答案】或 【解析】如解图,过N作NG⊥AB,交AB于点G,∵四边形ABCD为正方形,∴AB=AD=NG=
cm,在Rt△ABE中,∠BAE=30°,AB=
cm,∴BE=1
cm,AE=2
cm,∵F为AE的中点,∴AF=AE=1
cm,在Rt△ABE和Rt△NGM中,,∴Rt△ABE≌Rt△NGM(HL),∴BE=GM,∠BAE=∠MNG=30°,∠AEB=∠NMG=60°,∴∠AFM=90°,即MN⊥AE,在Rt△AMF中,∠FAM=30°,AF=1
cm,∴AM===
cm,由对称性得到AM′=BM=AB-AM=-=
cm,综上,AM的长等于或
cm.
解图
三、解答题
17.
【答案】
解:(1)结论:DM⊥EM,DM=EM.
[解析]延长EM交AD于H.
∵四边形ABCD是正方形,四边形EFGC是正方形,
∴∠ADE=∠DEF=90°,
AD=CD,
∴AD∥EF,
∴∠MAH=∠MFE,
∵AM=MF,∠AMH=∠FME,
∴△AMH≌△FME,
∴MH=ME,AH=EF=EC,∴DH=DE,
∵∠EDH=90°,
∴DM⊥EM,DM=ME.
(2)结论不变.DM⊥EM,DM=EM.
证明:延长EM交DA的延长线于H.
∵四边形ABCD是正方形,四边形EFGC是正方形,
∴∠ADE=∠DEF=90°,
AD=CD,
∴AD∥EF,
∴∠MAH=∠MFE,
∵AM=MF,∠AMH=∠FME,
∴△AMH≌△FME,
∴MH=ME,AH=EF=EC,
∴DH=DE,
∵∠EDH=90°,
∴DM⊥EM,DM=ME.
18.
【答案】
如图所示,将平移至,此时为的中点.
连接,则,
故.
由于,,
故.
19.
【答案】
当时,四边形是菱形.
∵,
∴四边形是平行四边形
∵中,
∴
∴
∵,
∴
∴
∴四边形是菱形.
20.
【答案】
【解析】
找点关于的对称点,
由正方形的性质可知,就是点关于的对称点,
连接、,由可知,
当且仅当、、三点共线时,的值最小,该最小值为.
八年下册
第十八章
平行四边形
章节训练
一、选择题
1.
如图,在?ABCD中,BM是∠ABC的平分线交CD于点M,且MC=2,?ABCD的周长是14,则DM等于( )
A.
1 B.
2 C.
3 D.
4
2.
以三角形的三个顶点作平行四边形,最多可以作(
)
A.2个
B.3个
C.4个
D.5个
3.
(2020·荆门)如图,菱形ABCD中,E,F分别是AD,BD的中点,若EF=5,则菱形ABCD的周长为(
)
A.20
B.30
C.40
D.50
(
D
A
C
B
F
E
)
4.
(2020·通辽)如图,AD是△ABC的中线,四边形ADCE是平行四边形,增加下列条件,能判断?ADCE是菱形的是( )
A.∠BAC=90°
B.∠DAE=90°
C.AB=AC
D.AB=AE
5.
如图,把一张矩形纸片ABCD沿对角线AC折叠,点B的对应点为B′,AB′与DC相交于点E,则下列结论一定正确的是( )
A.∠DAB′=∠CAB′
B.∠ACD=∠B′CD
C.AD=AE
D.AE=CE
6.
(2019?广西池河)如图,在△ABC中,D,E分别是AB,BC的中点,点F在DE延长线上,添加一个条件使四边形ADFC为平行四边形,则这个条件是
A.∠B=∠F
B.∠B=∠BCF
C.AC=CF
D.AD=CF
7.
(2020·临沂)如图,是面积为的内任意一点,的面积为,的面积为,则(
)
A.
B.
C.
D.的大小与点位置有关
8.
已知四边形的四条边长分别是,其中为对边,并且满足
则这个四边形是(
)
A.任意四边形
B.平行四边形
C.对角线相等的四边形
D.对角线垂直的四边形
二、填空题
9.
如图,在平行四边形中,,,于,则
.
10.
菱形中,、分别是、的中点,且,,那么等于
.
11.
如图,一活动菱形衣架中,菱形的边长均为若墙上钉子间的距离,则
度.
12.
已知正方形的边长是正方形的对角线,则
13.
如图所示,四边形ABCD的对角线相交于点O,若AB∥CD,请添加一个条件________(写一个即可),使四边形ABCD是平行四边形.
14.
如图,在ABCD中,E.F是对角线AC上两点,AE=EF=CD,∠ADF=90°,∠BCD=63°,则∠ADE的大小为__________.
15.
某台球桌为如图所示长方形,小球从沿角出击,恰好经过次碰撞到处,则=
16.
如图,正方形ABCD的面积为3
cm2,E为BC边上一点,∠BAE=30°,F为AE的中点,过点F作直线分别与AB,DC相交于点M,N.若MN=AE,则AM的长等于________cm.
三、解答题
17.
如图,已知正方形ABCD与正方形CEFG,M是AF的中点,连接DM,EM.
(1)如图①,点E在CD上,点G在BC的延长线上,判断DM,EM的数量关系与位置关系,请直接写出结论.
(2)如图②,点E在DC的延长线上,点G在BC上,(1)中结论是否仍然成立?请证明你的结论.
18.
如图所示,在长方形中,点是边的中点,点是边的中点,与交于点.若,求的度数.
19.
已知:如图,在平行四边形中,是边上的高,将沿方向平移,使点与点重合,得.若,当与满足什么数量关系时,四边形是菱形?证明你的结论.
20.
如图,正方形中,,是上的一点,且,是上的一动点,求的最小值.
人教版初中数学
八年下册
第十八章
平行四边形
章节训练-答案
一、选择题
1.
【答案】C 【解析】∵四边形ABCD是平行四边形,∴AB∥CD,∴∠ABM=∠CMB,∵BM平分∠ABC,∴∠ABM=∠CBM,∴∠CBM=∠CMB,∴CB=MC=2,∴AD=BC=2,∵?ABCD的周长是14,∴AB=CD=5,∴DM=DC-MC=3.
2.
【答案】B
3.
【答案】C
【解析】∵E,F分别是AD,BD的中点,∴EF是△DAB的中位线.∴AB=2EF=10.∵菱形的四边相等,∴菱形ABCD的周长=4AB=40.故选C.
4.
【答案】A
【解析】若∠BAC=90°,又因为AD是△ABC的中线,根据“直角三角形斜边上的中线等于斜边的一半”可得AD=CD,根据“有一组邻边相等的平行四边形是菱形”可证?ADCE是菱形.
5.
【答案】D 【解析】∵四边形ABCD为矩形,∴AB∥CD,∴∠ACD=∠BAC,由折叠的性质可得∠BAC
=∠EAC,
∴∠ACD=∠EAC,∴AE=CE.
6.
【答案】B
【解析】∵在△ABC中,D,E分别是AB,BC的中点,
∴DE是△ABC的中位线,∴DEAC.
A.根据∠B=∠F不能判定AC∥DF,即不能判定四边形ADFC为平行四边形,故本选项错误.
B.根据∠B=∠BCF可以判定CF∥AB,即CF∥AD,由“两组对边分别平行的四边形是平行四边形”得到四边形ADFC为平行四边形,故本选项正确.
C.根据AC=CF不能判定AC∥DF,即不能判定四边形ADFC为平行四边形,故本选项错误.
D.根据AD=CF,FD∥AC不能判定四边形ADFC为平行四边形,故本选项错误.
故选B.
7.
【答案】C
【解析】可以利用割补法对平行四边形进行分割,然后使分割后的图形与的面积,的面积发生关联,然后求出其数量关系,如下图,过点P作AD的平行线,分别交的边于点M、N:
.
8.
【答案】B
二、填空题
9.
【答案】
【解析】∵四边形是平行四边形
∴
又∵
∴,∴
又∵,∴
∴.
10.
【答案】
11.
【答案】
【解析】由题意可知:构成三角形为等边三角形
12.
【答案】
13.
【答案】AD∥BC(答案不唯一) 【解析】根据平行四边形的判定,在已有AB∥DC的条件下,可再加另一组对边平行即可证得它是平行四边形,即加“AD∥BC”.
14.
【答案】21°
【解析】设∠ADE=x,
∵AE=EF,∠ADF=90°,
∴∠DAE=∠ADE=x,DE=AF=AE=EF,
∵AE=EF=CD,∴DE=CD,
∴∠DCE=∠DEC=2x,
∵四边形ABCD是平行四边形,∴AD∥BC,
∴∠DAE=∠BCA=x,
∴∠DCE=∠BCD﹣∠BCA=63°﹣x,
∴2x=63°﹣x,解得x=21°,即∠ADE=21°;
故答案为:21°.
15.
【答案】
【解析】由图形可知:可推出
16.
【答案】或 【解析】如解图,过N作NG⊥AB,交AB于点G,∵四边形ABCD为正方形,∴AB=AD=NG=
cm,在Rt△ABE中,∠BAE=30°,AB=
cm,∴BE=1
cm,AE=2
cm,∵F为AE的中点,∴AF=AE=1
cm,在Rt△ABE和Rt△NGM中,,∴Rt△ABE≌Rt△NGM(HL),∴BE=GM,∠BAE=∠MNG=30°,∠AEB=∠NMG=60°,∴∠AFM=90°,即MN⊥AE,在Rt△AMF中,∠FAM=30°,AF=1
cm,∴AM===
cm,由对称性得到AM′=BM=AB-AM=-=
cm,综上,AM的长等于或
cm.
解图
三、解答题
17.
【答案】
解:(1)结论:DM⊥EM,DM=EM.
[解析]延长EM交AD于H.
∵四边形ABCD是正方形,四边形EFGC是正方形,
∴∠ADE=∠DEF=90°,
AD=CD,
∴AD∥EF,
∴∠MAH=∠MFE,
∵AM=MF,∠AMH=∠FME,
∴△AMH≌△FME,
∴MH=ME,AH=EF=EC,∴DH=DE,
∵∠EDH=90°,
∴DM⊥EM,DM=ME.
(2)结论不变.DM⊥EM,DM=EM.
证明:延长EM交DA的延长线于H.
∵四边形ABCD是正方形,四边形EFGC是正方形,
∴∠ADE=∠DEF=90°,
AD=CD,
∴AD∥EF,
∴∠MAH=∠MFE,
∵AM=MF,∠AMH=∠FME,
∴△AMH≌△FME,
∴MH=ME,AH=EF=EC,
∴DH=DE,
∵∠EDH=90°,
∴DM⊥EM,DM=ME.
18.
【答案】
如图所示,将平移至,此时为的中点.
连接,则,
故.
由于,,
故.
19.
【答案】
当时,四边形是菱形.
∵,
∴四边形是平行四边形
∵中,
∴
∴
∵,
∴
∴
∴四边形是菱形.
20.
【答案】
【解析】
找点关于的对称点,
由正方形的性质可知,就是点关于的对称点,
连接、,由可知,
当且仅当、、三点共线时,的值最小,该最小值为.
