反比例函数的图像和性质

(共46张PPT)
函数图象画法
列
表
描
点
连
线
描点法
反比例函数的图象又会是什么样子呢
你还记得作函数图象的一般步骤吗
用图象法表示函数关系时,首先在自变量的取值范围内取一些值,列表,描点,连线
x
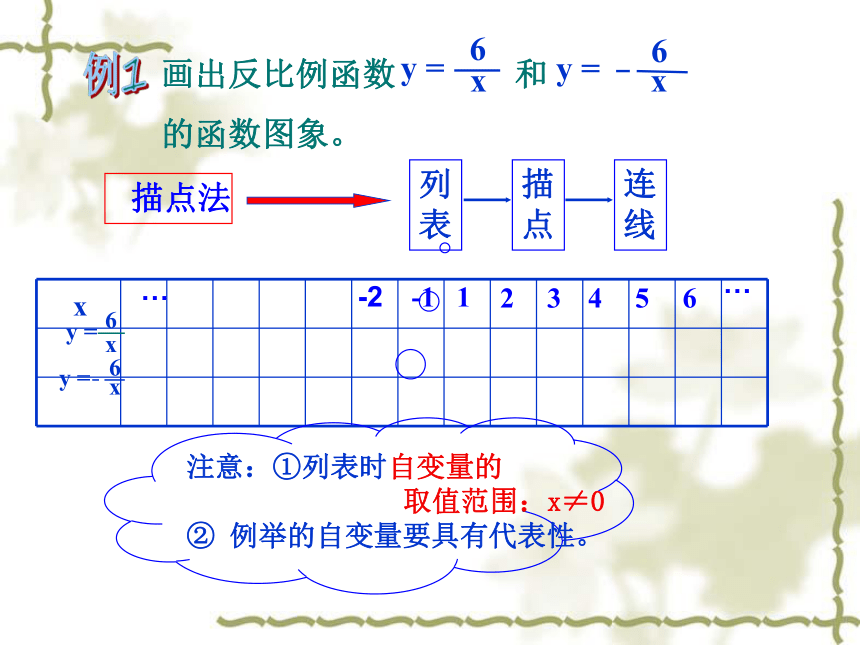
画出反比例函数 和
的函数图象。
y =
x
6
y =
x
6
列
表
描
点
连
线
y =
x
6
y =
x
6
描点法
注意：①列表时自变量的
取值范围：x≠0
② 例举的自变量要具有代表性。
1
2
3
4
5
6
-1
…
-2
…
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
y
x
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y
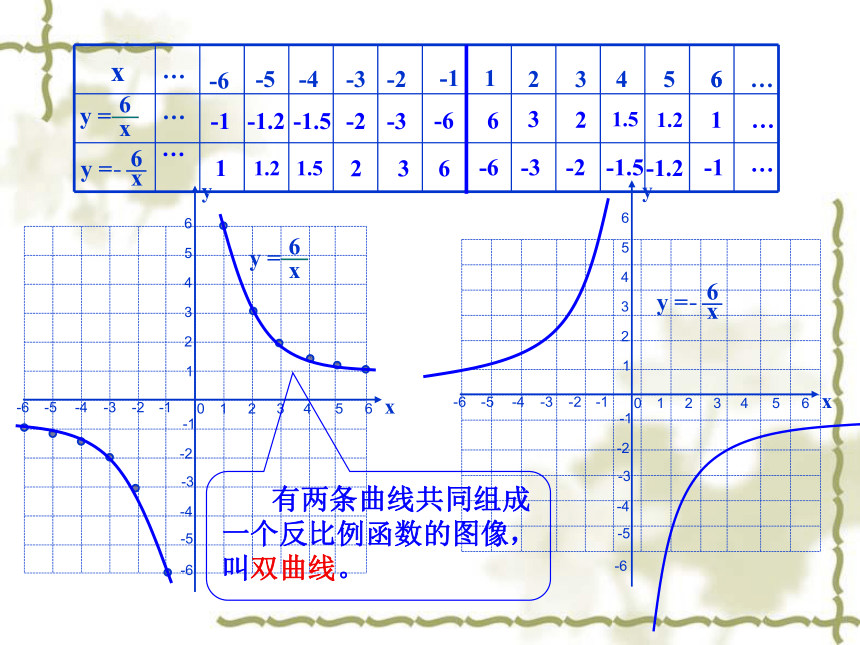
有两条曲线共同组成一个反比例函数的图像，叫双曲线。
x
1
6
2
3
3
2
4
1.5
5
1.2
6
1
6
-1
-6
-2
-3
-3
-1.5
-2
-4
-5
-1.2
-6
-1
…
…
…
…
-6
6
3
-3
2
-2
1.5
-1.5
1.2
-1.2
1
-1
…
…
y =
x
6
y =
x
6
y =
x
6
y =
x
6
从画反比例函数图象看,描点法还应注意什么
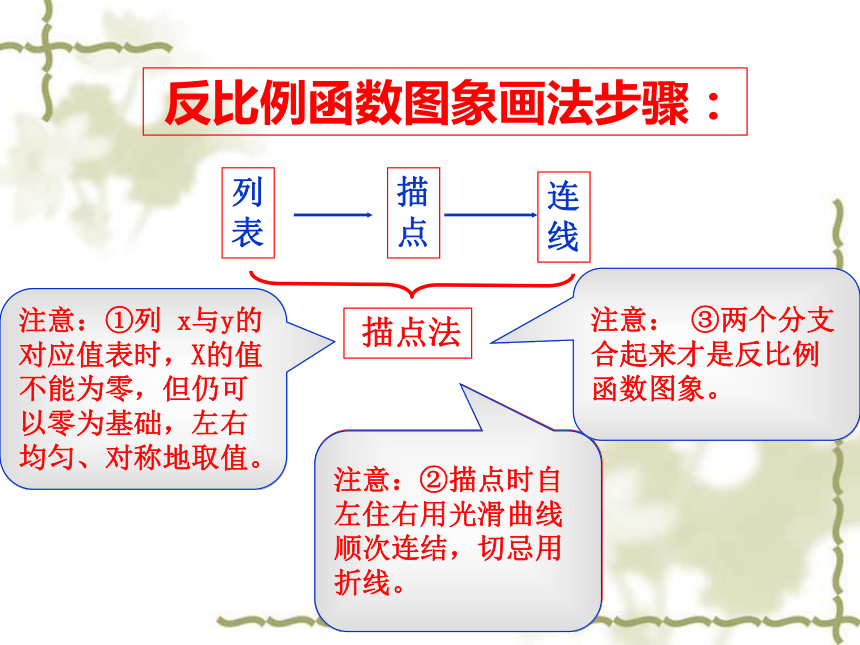
反比例函数图象画法步骤：
列
表
描
点
连
线
描点法
注意：①列 x与y的对应值表时，X的值不能为零，但仍可以零为基础，左右
均匀、对称地取值。
注意：②描点时自左住右用光滑曲线顺次连结，切忌用折线。
注意： ③两个分支合起来才是反比例函数图象。
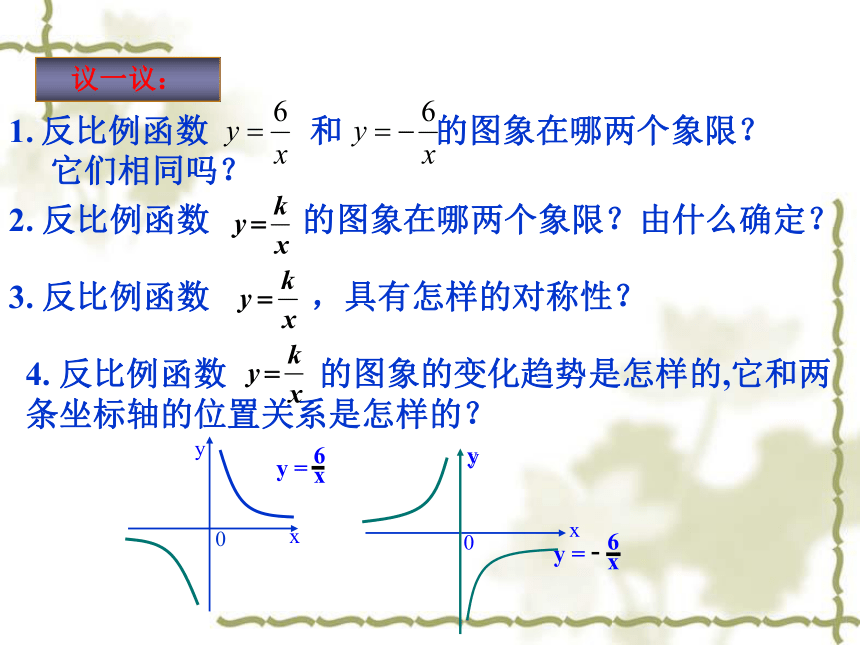
2. 反比例函数 的图象在哪两个象限？由什么确定？
3. 反比例函数 ，具有怎样的对称性？
4. 反比例函数 的图象的变化趋势是怎样的,它和两条坐标轴的位置关系是怎样的？
反比例函数 和 的图象在哪两个象限？
它们相同吗？
y =
x
6
x
y
0
y
x
y
x
6
y =
0
议一议：
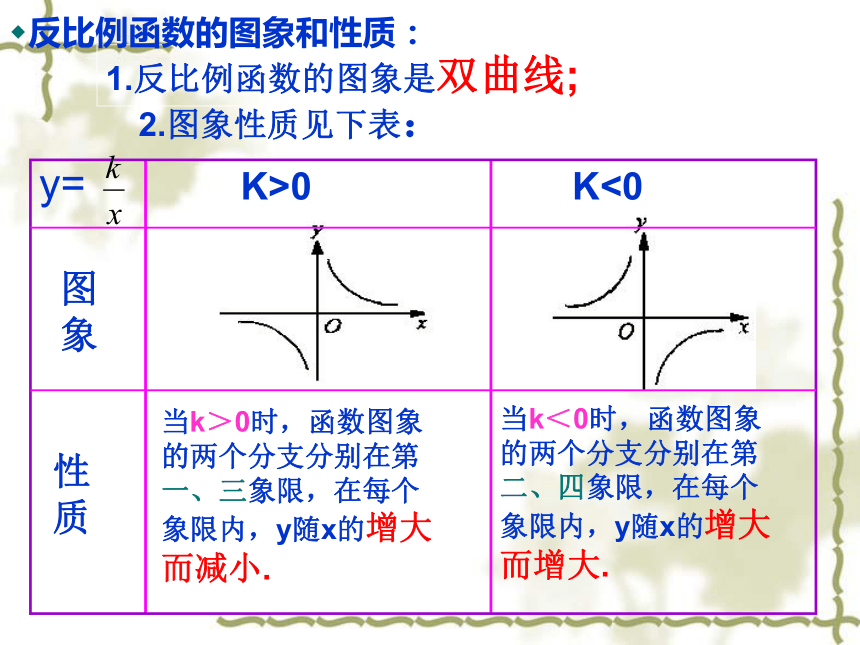
K>0
K<0
当k＞0时，函数图象
的两个分支分别在第
一、三象限，在每个
象限内，y随x的增大
而减小.
当k＜0时，函数图象
的两个分支分别在第
二、四象限，在每个
象限内，y随x的增大
而增大.
1.反比例函数的图象是双曲线;
2.图象性质见下表：
图
象
性质
y=
反比例函数的图象和性质：
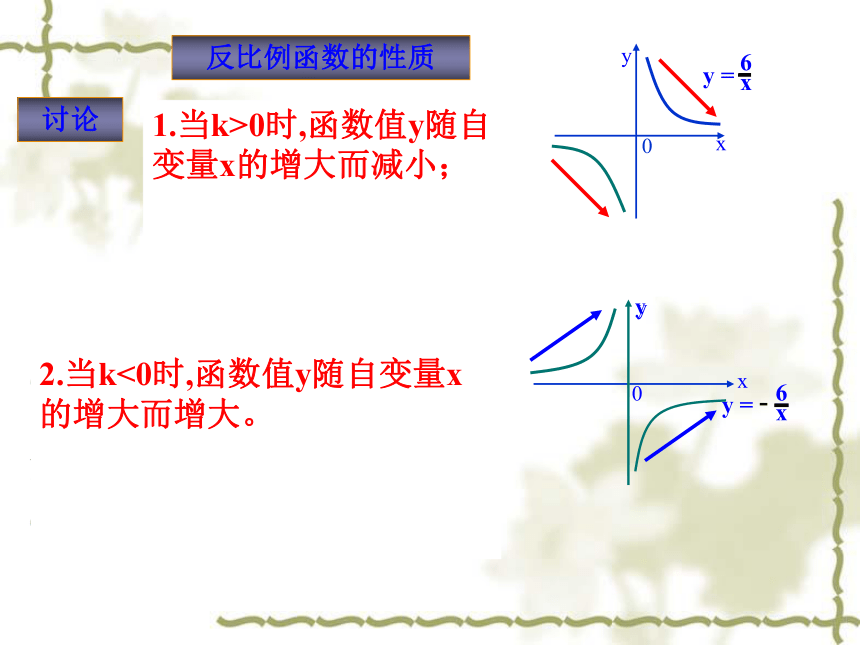
反比例函数的性质
①当k>0时，在图象所在的每一个象限内，当x增大时，y的变化规律？
②当k<0
请大家结合反比例函数
和 的函数图象，围绕以下两个问题分析反比例函数的性质。
y =
x
6
y =
x
6
1.当k>0时,函数值y随自变量x的增大而减小；
2.当k<0时,函数值y随自变量x的增大而增大。
讨论
y =
x
6
x
y
0
y
x
y
x
6
y =
0
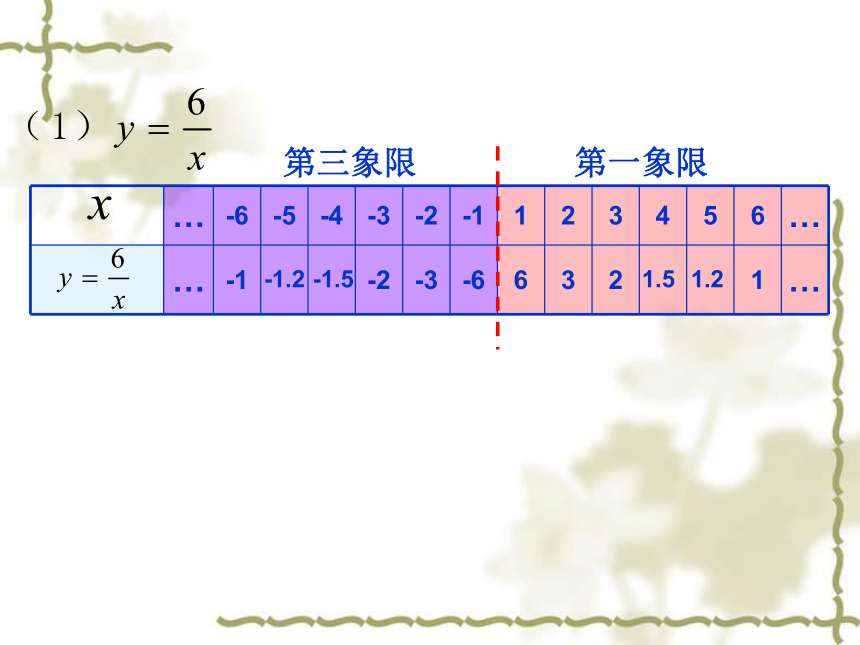
　 … -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 …
　 … -1 -2 -3 -6 6 3 2 1 …
第三象限
第一象限
-1.2
-1.5
1.5
1.2
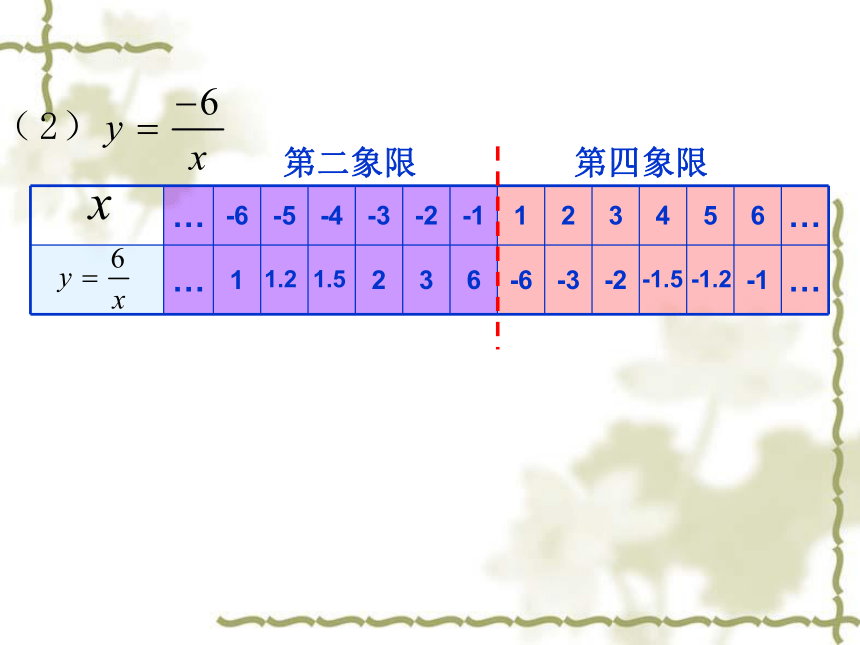
　 … -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 …
　 … 1 2 3 6 -6 -3 -2 -1 …
第二象限
第四象限
1.2
1.5
-1.5
-1.2
1、函数 的图象在第________象限,
在每一象限内，y 随x 的增大而_________.
2、 函数 的图象在第________象限,
在每一象限内，y 随x 的增大而_________.
3、函数 ,当x>0时,图象在第____象限,
y随x 的增大而_________.
一、三
二、四
一
减小
增大
减小
练一练
1
4.函数 的图象在第_____象限，
5. 双曲线 经过点（-3，___）
y =
x
5
y =
1
3x
二,四
9
1
6.函数 的图象在二、四象限，则m的取值范围是 ____ .
7.对于函数 ，当 x<0时，图象在第 ________象限.
m-2
x
y =
m < 2
三
y =
1
3x
五、大显身手：
1、已知反比例函数 （k≠0）的图象经过点
P（-1，2），则这个函数的图象位于（ ）。
A、第二、三象限 B、第一、三象限
C、第三、四象限 D、 第二、四象限
2、已知反比例函数 ，下列结论不正确 的是（ ）。
A、 图象经过点（1,1） B、图象在第一、三象限
C、当x＞1时，0＜y＜1 D、 当x＜0时， y随x的增大而增大。
D
D
（k≠0）的图象经过点（-3,2）和（m,-2），则m的值是（ ）。
A、 3 B、-3 C、6 D、 -6
4、若 +∣b+2∣=0，点M（a,b）在反比例函数
3、已知反比例函数
的图象上，下列结论正确的是（ ）。
A、
C、
D、
B、
A
D
例1:已知反比例函数y= (k≠0）的图象的一支如图。
（1）判断k是正数还是负数；
（2）求这个反比例函数的解析式；
y
x
0
（-4，2）
（3）补画这个反比例函数图象的另一支。
x
0
（-4，2）
y
例题解析,
图像的分支在第二象限，所以K ＜0
把(-4,2)代入y= 中，得到
K=-8
所以反比例函数的解析式；
y= -
k
x
8
x
正、反比例函数的图象与性质的比较：
正比例函数 反比例函数
解析式
增减性
直线
双曲线
k＞0，一、三象限；
k＜0，二、四象限．
k＞0，y随x的增大而增大；
k＞0，一、三象限；
k＜0，二、四象限．
k＜0，y随x的增大而减小．
k＞0，在每个象限y随x的增大而减小；
k＜0，在每个象限y随x的增大而增大．
图象
位置
K>0
K<0
当k＞0时，函数图象
的两个分支分别在第
一、三象限，在每个
象限内，y随x的增大
而减小.
当k＜0时，函数图象
的两个分支分别在第
二、四象限，在每个
象限内，y随x的增大
而增大.
1.反比例函数的图象是双曲线;
2.图象性质见下表：
图
象
性质
y=
反比例函数的图象和性质：
1.函数 的图象在第_____象限，
2. 双曲线 经过点（-3，___）
y =
x
5
y =
1
3x
3.函数 的图象在二、四象限，则m的取值范围是 ____ .
4.对于函数 ，当 x<0时，图象在第 ________象限.
m-2
x
y =
y =
1
3x
课前检测（10月31日）：

基础再现:
1.己知函数 的图象是双曲线,且y随x的增大而增大,
则m=______;
-1
2.如果反比例函数 的图象位于第二、四象限，那么m的范围为 .
m＞
任意一组变量的乘积是一个定值,即xy=k
长方形面积　 三角形的面积
面积不变性
︳m n︱ ＝︳K︱
P
D
o
y
x
x
y
o
M
N
p
（m,n）
（m,n）

P
D
o
y
x
1.如图,点P是反比例函数 图象上的一点,PD⊥x轴于D.则△POD的面积为 .
(m,n)
1
S△POD =　 OD·PD
　　
= 　
　　
=
变1:换一个角度： 双曲线 上任一点分别作x轴、y轴的垂线段，与x轴y轴围成矩形面积为12，求函数解析式。
如图
∵︳K︱ ＝12
∴k=±12
(X>0)
先由数（式）到形再由形到数（式）的数学思想
2.如图,点P是反比例函数 图象上的一点,PD⊥x轴于D.则△POD的面积为 .
3.如图,点P是反比例函数图象上的一点,过点P分别向x轴、y轴作垂线,若阴影部分面积为3,则这个反比例函数的关系式是 .
P
D
o
y
x
x
y
o
M
N
p
2
练一练
3

A. S1＞S2
B．S1C．S1=S2
D．S1与S2的大小关系
不能确定
c
如图，A、C是函数 的图象上的任意两点，过A作x轴的垂线，垂足为B，过C作y轴的垂线，垂足为D，记RtΔAOB的面积为S1，RtΔCOD的面积为S2,则（ ）
S1
S2
4、

(2007山东省中考题) 反比例函数y= 的图象
如图所示，点M是该函数图象上一点，MN垂直
于x轴，垂足是点N，如果S△MON=2， 则k的值
为( )
(A)2 (B)－2 (C) －4 (D) 4
N
M
x
y
O
C
5、
拓展:
6、在直角坐标系中,直线y=x+m-1与双曲线 在第一象限交于点A，与x轴交于点C，AB垂直于x轴，垂足为B，且S△AOB=2
（1）求m的值；
（2）求△ABC的面积。
y
x
O
A
B
C
（1）m=4
（2） S△ABC=8
相交于A、B两点．过 A作x轴的垂线、过B
作y轴的垂线，垂足分别为D、C，设梯形ABCD的
面积为S，则( )
A．S＝6 B．S=3
C．27. 如图，正比例函数 与反比例函数
x
y
A
B
C
D
O
B

变1:如图,A、B是函数y= 的图象上关于原点对称 的任意两点，AC∥y轴，BC∥x轴，则△ABC的面积S为（ ）
A）1 B）2
C）S>2 D)1A
B
C
O
x
y
B

8、图中两个三角形的面
积各是___
1
2
9、S⊿ABC的面积=____
２

(2007荆门市中考题改编)
10.下列图形中阴影部分的面积相等的是（　）
Ａ.①② Ｂ.②③ Ｃ.①③
C
1
4
4
m
n
2
1、(2006年重庆市)如图所示.如果函数y=-kx(k≠0)
与 图像交于A、B两点，过点A作AC垂直于y轴，垂足为点C，则△BOC的面积为 .
S ⊿BOC =S ⊿AOC
S⊿AOC = ∣-4 ∣= 2
D
拓展：

o
A
C
x
B
y
D
C
D
o
A
x
B
y
2、四边形ABCD的面积=_____
2

(2007荆州市中考题) 如图，D是反比例函数
的图像上一点，
过D作DE⊥x轴于E，DC⊥y轴
于C，一次函数y=-x+2与x轴交
于A点，四边形DEAC的面积
为4，求k的值．
A
E
D
C
O
x
y
F
B
解：当X=0时, y=2. 即 C (0 ,2）
3：
当y=0时, x=2. 即 A (2 ,0)
∴S⊿AOC =2
∴S四边形DCOE =4-2=2
∴K=-2

A
B
C
E
O
F
x
y
x
(2007武汉市)如图，已知双曲线　　　(x＞0)
经过矩形OABC边AB的中点F，交BC于点E，且四边形OEBF的面积为2，则k＝____。
2
S⊿AOF = S矩形AOCB
S⊿AOF = S四边形EOBF =1
O
A
C
D
4：
思索归纳

通过本堂课的学习，
你有什么收获吗？
1、S△AOF=
2、在一次函数、反比例函数的图象组合图形的面 积计算要注意选择恰当的分解方法.
3、在函数图形中的面积计算中，要充分利用好横、 纵坐标.
4、各种数学思想理解：归类思想、探究思想、转化思想、数形结合思想…….
5、根据面积求k值要注意图象的象限、K值的符号.；
思索归纳

如图，在平面直角坐标
系中，A为y轴正半轴上一点，过A作x轴的平行线，交函数 的图象于B，交函数
的图象于C，过C作y轴的平行线交x轴于D．四边形BODC的面积为 ．
7
(2007长春市)
E
8、
做一做：
1．用“＞”或“＜”填空：
　（1）已知　　　和　　　是反比例函数　　　的两对自变
　　　 量与函数的对应值．若　　　　　，则　　 　　 　．
　（2）已知　　　和　　　是反比例函数　　　 的两对自变
　　　 量与函数的对应值．若　　　　　，则　　 　　 　．
>
>
>
>
2．已知（　　 ），（　　 ），（ 　　 ）是反比例函数
　 的图象上的三个点，并且　　　　　　　　，则
　 　　　　　的大小关系是（　　）
　 （A）　　　　　　　　 （B）
（C）　 （D）
3．已知（　　 ），（ 　 ），（ 　　 ）是反比例函数
　 的图象上的三个点，则 的大小关系是
　　　　　　　　　　．
4．已知反比例函数 ．（1）当x＞5时，0　　y 1；
（2）当x≤5时，则y 　 1,或y＜　　（3）当y＞5时，求x
的取值范围.
C
<
<
≥
0
5、已知点（-1 ，y1）（2，y2）（3，y3）在反比例函数
（k＜0）的图象上，下列结论正确的是（ ）。
A、y1 ＞ y2 ＞y3 B、 y1＞y3＞y2
C、y3＞y1＞y2 D、y2 ＞y3＞y1
6、在同一直角坐标系中，正比例函数y=k1x与反比例函数y= k2∕x没有交点，
则两个常数的乘积k1 ·k2的取值范围是 。
7、已知一次函数y=kx+b的图象经过第二、三、四象限，则反比例函数
的图象在（ ）。
A、 第一、二象限 B、第三、四象限
C、第一、三象限 D、 第二、四象限
B
k1 ·k2 ＜0
C
想一想:
1、反比例函数 与正比例函数 在同一坐标系中的图象不可能的是（ ）
（A）
（B）
（C）
（D）
D
总结 ：反比例函数的图象性质特征：
图象是双曲线
当k>0时,双曲线分别位于第一,三象限内
当k<0时, 双曲线分别位于第二,四象限内
当k>0时,在每一象限内,y随x的增大而减小
当k<0时,在每一象限内,y随x的增大而增大
双曲线无限接近于x、y轴,但永远不会与坐标轴相交
双曲线既是轴对称图形又是中心对称图形.
任意一组变量的乘积是一个定值,即xy=k
形状
位置
增减性
变化趋势
对称性
面积不变性
长方形面积 ︳m n︱ ＝︳K︱
P(m,n)
A
o
y
x
B
1.通过本节课的学习，你有什么收获？还有什么困惑吗？
2.你对自己本节课的表现满意吗？为什么？
同学们,再见!