湘教版八年级数学下册 1.1.2含30°角的直角三角形的性质同步练习(word版含答案)
文档属性
| 名称 | 湘教版八年级数学下册 1.1.2含30°角的直角三角形的性质同步练习(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 171.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-19 21:17:12 | ||
图片预览




文档简介
1.1.2含30°角的直角三角形的性质
1.如图,在△ABC中,∠BAC=90°,∠C=30°,AD⊥BC,垂足为D,则BD与BC的数量关系是( )
A.BD=BC B.BD=BC
C.BD=BC D.BD=BC
2.如图,在△ABC中,∠BAC=120°,AB=AC,AD是高,DE⊥AB于点E,且AE=2,则AB的长为( )
A.4 B.6
C.7 D.8
3.【模拟·永州】在△ABC中,∠A∶∠B∶∠C=1∶2∶3,最短边BC=3 cm,则最长边AB的长为( )
A.9 cm B.8 cm C.7 cm D.6 cm
4.如图,在△ABC中,BC=8,AB=10,S△ABC=20,则∠B的度数是( )
A.15° B.30°
C.45° D.60°
如图,在△ABC中,∠C=90°,∠A=30°,BD为△ABC的角平分线,若AC=12,则在△ABD中,AB边上的高为( )
A.3 B.4 C.5 D.6
6.【中考·海南】如图,在平行四边形ABCD中,将△ADC沿AC折叠后,点D恰好落在DC延长线上的点E处.若∠B=60°,AB=3,则△ADE的周长为( )
A.12 B.15
C.18 D.21
7.【教材改编题】如图是某建筑物的屋顶架的示意图,D是斜梁AB的中点,立柱BC,DE都垂直于横梁AC,DE=2米,∠A=30°,则AB等于( )
A.8米 B.4米
C.2米 D.1米
8.如图是某商场一楼与二楼之间的手扶电梯示意图,其中AB,CD分别表示一楼、二楼地面的水平线,∠ABC=150°,BC的长是8 m,则乘电梯从点B到点C上升的高度h是( )
A.3 m B.4 m
C.5 m D.6 m
9.如图,一辆货车车厢底板离地面的高度为1.5 m,为了方便卸货,常用一块木板搭成一个斜面,要使斜面与水平地面的夹角不大于30°,则这块木板的长度至少为( )
A.3 m B.2.5 m
C.2.6 m D.0.75 m
10.设计一张折叠型方桌如图所示,若AO=BO=50 cm,CO=DO=30 cm,将桌子放平后,要使AB离地面的高度为40 cm,则两条桌腿需要叉开的∠AOB应为( )
A.60° B.90°
C.120° D.150°
11.【中考·黔西南州】如图,在Rt△ABC中,∠C=90°,点D在线段BC上,且∠B=30°,∠ADC=60°,BC=3 ,则BD的长度为___
12.如图,在Rt△ABC中,∠ACB=90°,AB边的垂直平分线交AB于点E,交BC于点D,且BD=18,AC=9,则∠B=____.
13.如图,在△ABC中,∠C=90°,∠A=30°,其周长为3+3 ,AC=3,则BC的长为________.
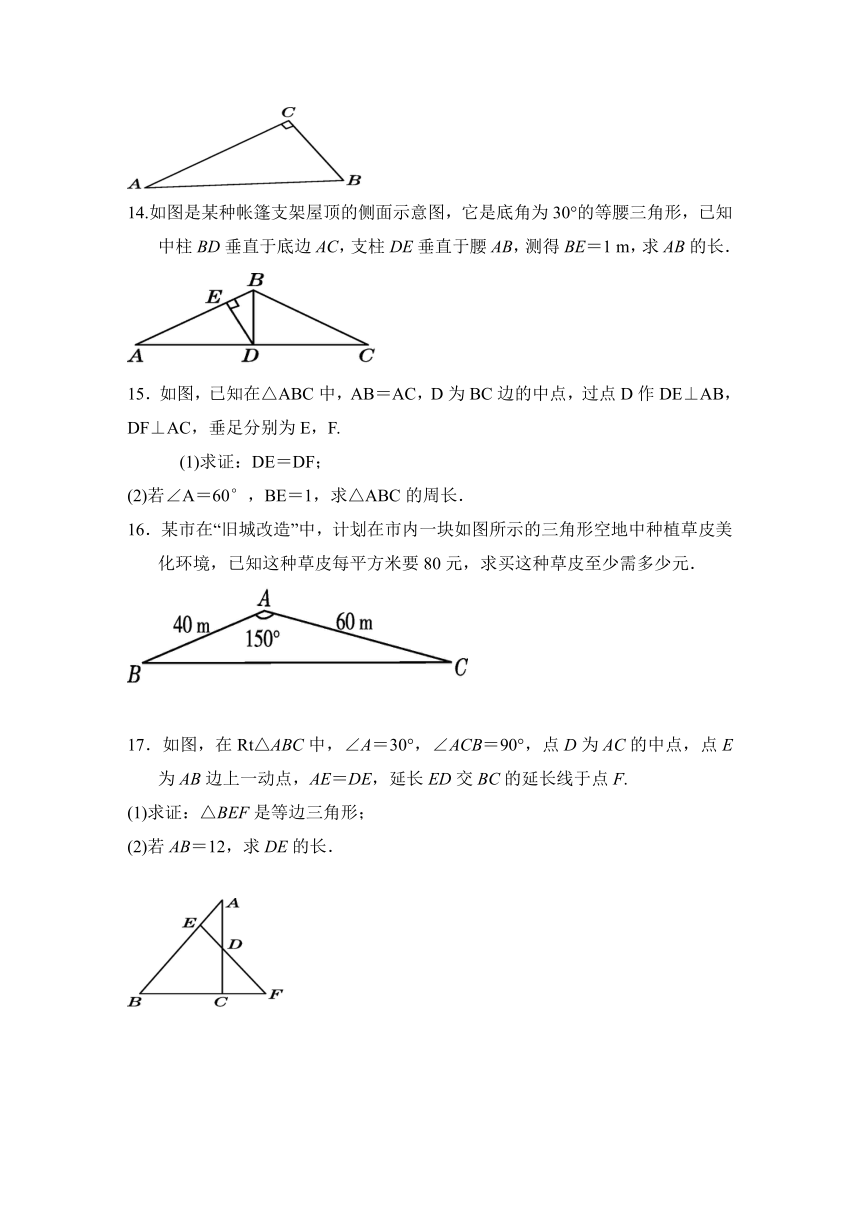
14.如图是某种帐篷支架屋顶的侧面示意图,它是底角为30°的等腰三角形,已知中柱BD垂直于底边AC,支柱DE垂直于腰AB,测得BE=1 m,求AB的长.
15.如图,已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.
(1)求证:DE=DF;
(2)若∠A=60°,BE=1,求△ABC的周长.
16.某市在“旧城改造”中,计划在市内一块如图所示的三角形空地中种植草皮美化环境,已知这种草皮每平方米要80元,求买这种草皮至少需多少元.
17.如图,在Rt△ABC中,∠A=30°,∠ACB=90°,点D为AC的中点,点E为AB边上一动点,AE=DE,延长ED交BC的延长线于点F.
(1)求证:△BEF是等边三角形;
(2)若AB=12,求DE的长.
1.1.2含30°角的直角三角形的性质
1.如图,在△ABC中,∠BAC=90°,∠C=30°,AD⊥BC,垂足为D,则BD与BC的数量关系是( C )
A.BD=BC B.BD=BC
C.BD=BC D.BD=BC
2.如图,在△ABC中,∠BAC=120°,AB=AC,AD是高,DE⊥AB于点E,且AE=2,则AB的长为( D )
A.4 B.6
C.7 D.8
3.【模拟·永州】在△ABC中,∠A∶∠B∶∠C=1∶2∶3,最短边BC=3 cm,则最长边AB的长为( D )
A.9 cm B.8 cm C.7 cm D.6 cm
【点拨】设∠A,∠B,∠C的度数分别为k,2k,3k,则k+2k+3k=180°,解得k=30°,∴2k=60°,3k=90°.∵最短边BC=3 cm,∴最长边AB=2BC=2×3=6(cm).
4.如图,在△ABC中,BC=8,AB=10,S△ABC=20,则∠B的度数是( B )
A.15° B.30°
C.45° D.60°
【点拨】过点C作CD⊥AB于点D.∵ AB=10,S△ABC=20,
∴CD=4.∵在Rt△BCD中, BC=8,∴CD=BC.
∴∠B=30°.故选B.
如图,在△ABC中,∠C=90°,∠A=30°,BD为△ABC的角平分线,若AC=12,则在△ABD中,AB边上的高为( B )
A.3 B.4 C.5 D.6
【点拨】过D作DE⊥AB于E.∵∠C=90°,∠A=30°,
∴∠CBA=60°.∵BD平分∠CBA,∴∠DBA=∠DBC=30°=∠A,
∴AD=BD,CD=BD,∴CD=AD.∵AD+CD=AC=12,∴CD=4.
∵DE⊥AB,∴∠DEB=90°=∠C.在△DBE与△DBC中,
∴△DBE≌△DBC.∴DE=CD=4.
6.【中考·海南】如图,在平行四边形ABCD中,将△ADC沿AC折叠后,点D恰好落在DC延长线上的点E处.若∠B=60°,AB=3,则△ADE的周长为( C )
A.12 B.15
C.18 D.21
【点拨】∵四边形ABCD是平行四边形,∴AB∥CD,AD∥BC,CD=AB=3,∴∠BAD=180°-∠B=120°,
∴∠D=180°-∠BAD=60°,由折叠知CE=CD=3,AE=AD,
∴DE=6,△ADE是等边三角形,∴△ADE的周长为3DE=18.
7.【教材改编题】如图是某建筑物的屋顶架的示意图,D是斜梁AB的中点,立柱BC,DE都垂直于横梁AC,DE=2米,∠A=30°,则AB等于( A )
A.8米 B.4米
C.2米 D.1米
【点拨】∵∠A=30°,DE⊥AC,∴DE=AD,又DE=2米,∴AD=4米.∵D是AB的中点,∴AB=2AD=8米.
8.如图是某商场一楼与二楼之间的手扶电梯示意图,其中AB,CD分别表示一楼、二楼地面的水平线,∠ABC=150°,BC的长是8 m,则乘电梯从点B到点C上升的高度h是( B )
A.3 m B.4 m
C.5 m D.6 m
【点拨】如图,过点C作CE⊥AB交AB 的延长线于E,
∵∠ABC=150°,∴∠CBE=30°,∴CE=BC.又BC=8 m,
∴CE=4 m,即h=4 m.
9.如图,一辆货车车厢底板离地面的高度为1.5 m,为了方便卸货,常用一块木板搭成一个斜面,要使斜面与水平地面的夹角不大于30°,则这块木板的长度至少为( A )
A.3 m B.2.5 m
C.2.6 m D.0.75 m
10.设计一张折叠型方桌如图所示,若AO=BO=50 cm,CO=DO=30 cm,将桌子放平后,要使AB离地面的高度为40 cm,则两条桌腿需要叉开的∠AOB应为( C )
A.60° B.90°
C.120° D.150°
【点拨】过点D作DE⊥AB交AB于E.在Rt△ADE中,AD=OA+OD=50+30=80(cm),易知DE=40 cm,∴DE=AD.∴∠BAD=30°.∵OA=OB,∴∠ABC=∠BAD=30°.∴∠AOB=180°-2×30°=120°.故选C.
11.【中考·黔西南州】如图,在Rt△ABC中,∠C=90°,点D在线段BC上,且∠B=30°,∠ADC=60°,BC=3 ,则BD的长度为___2
12.如图,在Rt△ABC中,∠ACB=90°,AB边的垂直平分线交AB于点E,交BC于点D,且BD=18,AC=9,则∠B=____15°.____.
【点拨】∵DE是AB的垂直平分线,∴AD=BD.∴∠B=∠BAD.又BD=18,AC=9,∴AC=AD.又∠ACB=90°,∴∠ADC=30°.∵∠ADC=∠B+∠BAD,∴∠ADC=2∠B,∴∠B=15°.
13.如图,在△ABC中,∠C=90°,∠A=30°,其周长为3+3 ,AC=3,则BC的长为________.
【点拨】∵在Rt△ABC中,∠C=90°,∠A=30°,∴AB=2BC.∵AB+BC+AC=3 +3,AC=3,∴2BC+BC+3=3 +3,即3BC=3 .∴BC=.
14.如图是某种帐篷支架屋顶的侧面示意图,它是底角为30°的等腰三角形,已知中柱BD垂直于底边AC,支柱DE垂直于腰AB,测得BE=1 m,求AB的长.
解:∵BD⊥AC,DE⊥AB,∴∠ADB=∠DEB=∠AED=90°.
又∵∠A=30°,∴∠ADE=90°-30°=60°,AB=2BD.
∴∠BDE=90°-60°=30°.∴BD=2BE.
∵BE=1 m,∴BD=2 m.∴AB=2BD=4 m.
15.如图,已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.
(1)求证:DE=DF;
(2)若∠A=60°,BE=1,求△ABC的周长.
证明:(1)∵DE⊥AB,DF⊥AC,∴∠BED=∠CFD=90°.
∵AB=AC,∴∠B=∠C.
∵D是BC的中点,∴BD=CD.
在△BED和△CFD中,∠BED=∠CFD,∠B=∠C,BD=CD,
∴△BED≌△CFD(AAS).
∴DE=DF.
(2):∵AB=AC,∠A=60°,∴△ABC为等边三角形,
∴∠B=60°.∵∠BED=90°,∴∠BDE=30°,∴BE=BD.
∵BE=1,∴BD=2,∴BC=2BD=4,
∴△ABC的周长为3BC=12.
16.某市在“旧城改造”中,计划在市内一块如图所示的三角形空地中种植草皮美化环境,已知这种草皮每平方米要80元,求买这种草皮至少需多少元.
解:如图,过点C作CD⊥BA,交BA的延长线于点D.
∵∠BAC=150°,∴∠DAC=30°.
∵CD⊥BD,AC=60 m,∴CD=AC=30 m.
又∵AB=40 m,∴S△ABC=AB·CD=×40×30=600(m2).
∵这种草皮每平方米要80元,
∴买这种草皮至少需600×80=48 000(元).
17.如图,在Rt△ABC中,∠A=30°,∠ACB=90°,点D为AC的中点,点E为AB边上一动点,AE=DE,延长ED交BC的延长线于点F.
(1)求证:△BEF是等边三角形;
(2)若AB=12,求DE的长.
证明:(1)∵∠A=30°,∠ACB=90°,∴∠B=60°.
∵AE=DE,∴∠ADE=∠A=30°,
∴∠BEF=∠A+∠ADE=60°,∴△BEF 是等边三角形.
(2):如图,在 EF 上截取 FG=CF,连接 CG.
由(1)知△BEF是等边三角形,∴∠F=60°,
又FG=CF,∴△CFG为等边三角形,
∴∠FGC=60°=∠BEF. ∴∠AED=∠CGD.
∵点D为AC的中点,∴AD=CD.
1.如图,在△ABC中,∠BAC=90°,∠C=30°,AD⊥BC,垂足为D,则BD与BC的数量关系是( )
A.BD=BC B.BD=BC
C.BD=BC D.BD=BC
2.如图,在△ABC中,∠BAC=120°,AB=AC,AD是高,DE⊥AB于点E,且AE=2,则AB的长为( )
A.4 B.6
C.7 D.8
3.【模拟·永州】在△ABC中,∠A∶∠B∶∠C=1∶2∶3,最短边BC=3 cm,则最长边AB的长为( )
A.9 cm B.8 cm C.7 cm D.6 cm
4.如图,在△ABC中,BC=8,AB=10,S△ABC=20,则∠B的度数是( )
A.15° B.30°
C.45° D.60°
如图,在△ABC中,∠C=90°,∠A=30°,BD为△ABC的角平分线,若AC=12,则在△ABD中,AB边上的高为( )
A.3 B.4 C.5 D.6
6.【中考·海南】如图,在平行四边形ABCD中,将△ADC沿AC折叠后,点D恰好落在DC延长线上的点E处.若∠B=60°,AB=3,则△ADE的周长为( )
A.12 B.15
C.18 D.21
7.【教材改编题】如图是某建筑物的屋顶架的示意图,D是斜梁AB的中点,立柱BC,DE都垂直于横梁AC,DE=2米,∠A=30°,则AB等于( )
A.8米 B.4米
C.2米 D.1米
8.如图是某商场一楼与二楼之间的手扶电梯示意图,其中AB,CD分别表示一楼、二楼地面的水平线,∠ABC=150°,BC的长是8 m,则乘电梯从点B到点C上升的高度h是( )
A.3 m B.4 m
C.5 m D.6 m
9.如图,一辆货车车厢底板离地面的高度为1.5 m,为了方便卸货,常用一块木板搭成一个斜面,要使斜面与水平地面的夹角不大于30°,则这块木板的长度至少为( )
A.3 m B.2.5 m
C.2.6 m D.0.75 m
10.设计一张折叠型方桌如图所示,若AO=BO=50 cm,CO=DO=30 cm,将桌子放平后,要使AB离地面的高度为40 cm,则两条桌腿需要叉开的∠AOB应为( )
A.60° B.90°
C.120° D.150°
11.【中考·黔西南州】如图,在Rt△ABC中,∠C=90°,点D在线段BC上,且∠B=30°,∠ADC=60°,BC=3 ,则BD的长度为___
12.如图,在Rt△ABC中,∠ACB=90°,AB边的垂直平分线交AB于点E,交BC于点D,且BD=18,AC=9,则∠B=____.
13.如图,在△ABC中,∠C=90°,∠A=30°,其周长为3+3 ,AC=3,则BC的长为________.
14.如图是某种帐篷支架屋顶的侧面示意图,它是底角为30°的等腰三角形,已知中柱BD垂直于底边AC,支柱DE垂直于腰AB,测得BE=1 m,求AB的长.
15.如图,已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.
(1)求证:DE=DF;
(2)若∠A=60°,BE=1,求△ABC的周长.
16.某市在“旧城改造”中,计划在市内一块如图所示的三角形空地中种植草皮美化环境,已知这种草皮每平方米要80元,求买这种草皮至少需多少元.
17.如图,在Rt△ABC中,∠A=30°,∠ACB=90°,点D为AC的中点,点E为AB边上一动点,AE=DE,延长ED交BC的延长线于点F.
(1)求证:△BEF是等边三角形;
(2)若AB=12,求DE的长.
1.1.2含30°角的直角三角形的性质
1.如图,在△ABC中,∠BAC=90°,∠C=30°,AD⊥BC,垂足为D,则BD与BC的数量关系是( C )
A.BD=BC B.BD=BC
C.BD=BC D.BD=BC
2.如图,在△ABC中,∠BAC=120°,AB=AC,AD是高,DE⊥AB于点E,且AE=2,则AB的长为( D )
A.4 B.6
C.7 D.8
3.【模拟·永州】在△ABC中,∠A∶∠B∶∠C=1∶2∶3,最短边BC=3 cm,则最长边AB的长为( D )
A.9 cm B.8 cm C.7 cm D.6 cm
【点拨】设∠A,∠B,∠C的度数分别为k,2k,3k,则k+2k+3k=180°,解得k=30°,∴2k=60°,3k=90°.∵最短边BC=3 cm,∴最长边AB=2BC=2×3=6(cm).
4.如图,在△ABC中,BC=8,AB=10,S△ABC=20,则∠B的度数是( B )
A.15° B.30°
C.45° D.60°
【点拨】过点C作CD⊥AB于点D.∵ AB=10,S△ABC=20,
∴CD=4.∵在Rt△BCD中, BC=8,∴CD=BC.
∴∠B=30°.故选B.
如图,在△ABC中,∠C=90°,∠A=30°,BD为△ABC的角平分线,若AC=12,则在△ABD中,AB边上的高为( B )
A.3 B.4 C.5 D.6
【点拨】过D作DE⊥AB于E.∵∠C=90°,∠A=30°,
∴∠CBA=60°.∵BD平分∠CBA,∴∠DBA=∠DBC=30°=∠A,
∴AD=BD,CD=BD,∴CD=AD.∵AD+CD=AC=12,∴CD=4.
∵DE⊥AB,∴∠DEB=90°=∠C.在△DBE与△DBC中,
∴△DBE≌△DBC.∴DE=CD=4.
6.【中考·海南】如图,在平行四边形ABCD中,将△ADC沿AC折叠后,点D恰好落在DC延长线上的点E处.若∠B=60°,AB=3,则△ADE的周长为( C )
A.12 B.15
C.18 D.21
【点拨】∵四边形ABCD是平行四边形,∴AB∥CD,AD∥BC,CD=AB=3,∴∠BAD=180°-∠B=120°,
∴∠D=180°-∠BAD=60°,由折叠知CE=CD=3,AE=AD,
∴DE=6,△ADE是等边三角形,∴△ADE的周长为3DE=18.
7.【教材改编题】如图是某建筑物的屋顶架的示意图,D是斜梁AB的中点,立柱BC,DE都垂直于横梁AC,DE=2米,∠A=30°,则AB等于( A )
A.8米 B.4米
C.2米 D.1米
【点拨】∵∠A=30°,DE⊥AC,∴DE=AD,又DE=2米,∴AD=4米.∵D是AB的中点,∴AB=2AD=8米.
8.如图是某商场一楼与二楼之间的手扶电梯示意图,其中AB,CD分别表示一楼、二楼地面的水平线,∠ABC=150°,BC的长是8 m,则乘电梯从点B到点C上升的高度h是( B )
A.3 m B.4 m
C.5 m D.6 m
【点拨】如图,过点C作CE⊥AB交AB 的延长线于E,
∵∠ABC=150°,∴∠CBE=30°,∴CE=BC.又BC=8 m,
∴CE=4 m,即h=4 m.
9.如图,一辆货车车厢底板离地面的高度为1.5 m,为了方便卸货,常用一块木板搭成一个斜面,要使斜面与水平地面的夹角不大于30°,则这块木板的长度至少为( A )
A.3 m B.2.5 m
C.2.6 m D.0.75 m
10.设计一张折叠型方桌如图所示,若AO=BO=50 cm,CO=DO=30 cm,将桌子放平后,要使AB离地面的高度为40 cm,则两条桌腿需要叉开的∠AOB应为( C )
A.60° B.90°
C.120° D.150°
【点拨】过点D作DE⊥AB交AB于E.在Rt△ADE中,AD=OA+OD=50+30=80(cm),易知DE=40 cm,∴DE=AD.∴∠BAD=30°.∵OA=OB,∴∠ABC=∠BAD=30°.∴∠AOB=180°-2×30°=120°.故选C.
11.【中考·黔西南州】如图,在Rt△ABC中,∠C=90°,点D在线段BC上,且∠B=30°,∠ADC=60°,BC=3 ,则BD的长度为___2
12.如图,在Rt△ABC中,∠ACB=90°,AB边的垂直平分线交AB于点E,交BC于点D,且BD=18,AC=9,则∠B=____15°.____.
【点拨】∵DE是AB的垂直平分线,∴AD=BD.∴∠B=∠BAD.又BD=18,AC=9,∴AC=AD.又∠ACB=90°,∴∠ADC=30°.∵∠ADC=∠B+∠BAD,∴∠ADC=2∠B,∴∠B=15°.
13.如图,在△ABC中,∠C=90°,∠A=30°,其周长为3+3 ,AC=3,则BC的长为________.
【点拨】∵在Rt△ABC中,∠C=90°,∠A=30°,∴AB=2BC.∵AB+BC+AC=3 +3,AC=3,∴2BC+BC+3=3 +3,即3BC=3 .∴BC=.
14.如图是某种帐篷支架屋顶的侧面示意图,它是底角为30°的等腰三角形,已知中柱BD垂直于底边AC,支柱DE垂直于腰AB,测得BE=1 m,求AB的长.
解:∵BD⊥AC,DE⊥AB,∴∠ADB=∠DEB=∠AED=90°.
又∵∠A=30°,∴∠ADE=90°-30°=60°,AB=2BD.
∴∠BDE=90°-60°=30°.∴BD=2BE.
∵BE=1 m,∴BD=2 m.∴AB=2BD=4 m.
15.如图,已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.
(1)求证:DE=DF;
(2)若∠A=60°,BE=1,求△ABC的周长.
证明:(1)∵DE⊥AB,DF⊥AC,∴∠BED=∠CFD=90°.
∵AB=AC,∴∠B=∠C.
∵D是BC的中点,∴BD=CD.
在△BED和△CFD中,∠BED=∠CFD,∠B=∠C,BD=CD,
∴△BED≌△CFD(AAS).
∴DE=DF.
(2):∵AB=AC,∠A=60°,∴△ABC为等边三角形,
∴∠B=60°.∵∠BED=90°,∴∠BDE=30°,∴BE=BD.
∵BE=1,∴BD=2,∴BC=2BD=4,
∴△ABC的周长为3BC=12.
16.某市在“旧城改造”中,计划在市内一块如图所示的三角形空地中种植草皮美化环境,已知这种草皮每平方米要80元,求买这种草皮至少需多少元.
解:如图,过点C作CD⊥BA,交BA的延长线于点D.
∵∠BAC=150°,∴∠DAC=30°.
∵CD⊥BD,AC=60 m,∴CD=AC=30 m.
又∵AB=40 m,∴S△ABC=AB·CD=×40×30=600(m2).
∵这种草皮每平方米要80元,
∴买这种草皮至少需600×80=48 000(元).
17.如图,在Rt△ABC中,∠A=30°,∠ACB=90°,点D为AC的中点,点E为AB边上一动点,AE=DE,延长ED交BC的延长线于点F.
(1)求证:△BEF是等边三角形;
(2)若AB=12,求DE的长.
证明:(1)∵∠A=30°,∠ACB=90°,∴∠B=60°.
∵AE=DE,∴∠ADE=∠A=30°,
∴∠BEF=∠A+∠ADE=60°,∴△BEF 是等边三角形.
(2):如图,在 EF 上截取 FG=CF,连接 CG.
由(1)知△BEF是等边三角形,∴∠F=60°,
又FG=CF,∴△CFG为等边三角形,
∴∠FGC=60°=∠BEF. ∴∠AED=∠CGD.
∵点D为AC的中点,∴AD=CD.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
