5.4 密度知识的应用—沪科版八年级物理全册课件(共22张PPT)
文档属性
| 名称 | 5.4 密度知识的应用—沪科版八年级物理全册课件(共22张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 774.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-02-19 22:04:49 | ||
图片预览






文档简介
5.3 密度知识的应用
怎样鉴别戒指是不是纯金的?
怎样知道矿石是什么物质的?
怎样知道一大卷细铜丝的长度?
?
矗立在天安门广场的人民英雄纪念碑,它的碑心石是一整块巨大的花岗岩,碑身高37.94m,由413块花岗岩石块砌成,在长14.7m、宽2.9m、厚1m的碑心石上刻着“人民英雄永垂不朽”.怎样知道它的质量?
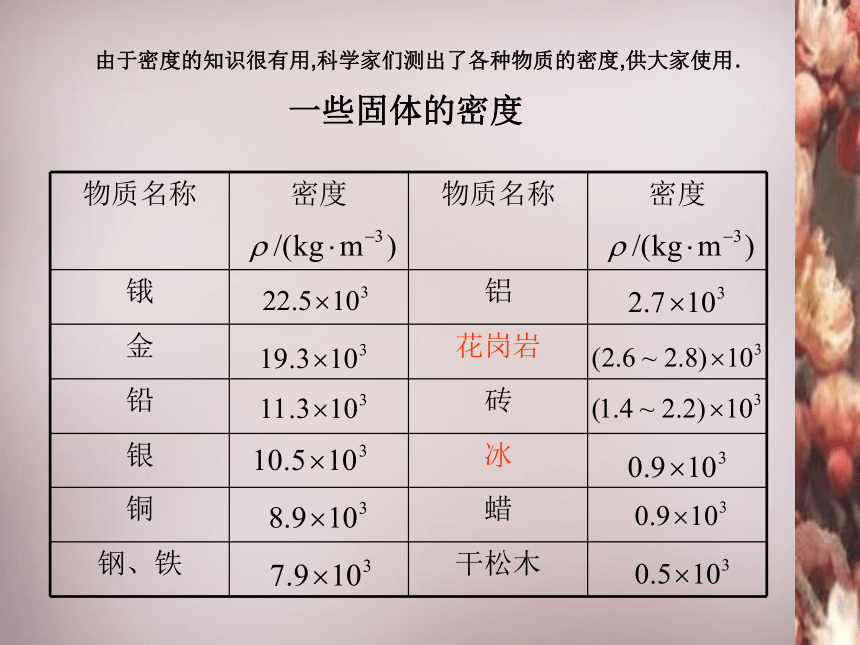
由于密度的知识很有用,科学家们测出了各种物质的密度,供大家使用.
物质名称
密度
物质名称
密度
锇
铝
金
花岗岩
铅
砖
银
冰
铜
蜡
钢、铁
干松木
一些固体的密度
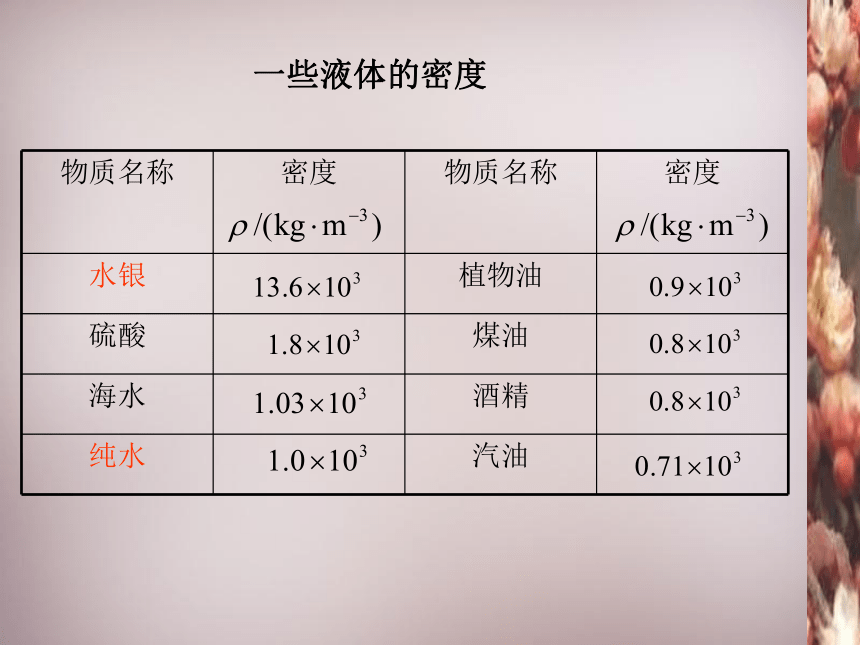
一些液体的密度
物质名称
密度
物质名称
密度
水银
植物油
硫酸
煤油
海水
酒精
纯水
汽油
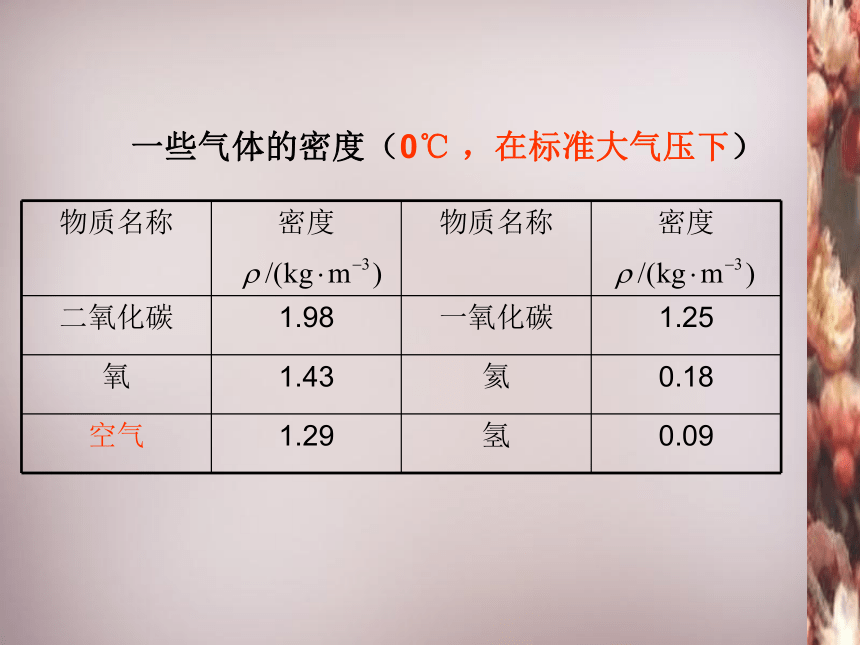
一些气体的密度(0℃ ,在标准大气压下)
物质名称
密度
物质名称
密度
二氧化碳
1.98
一氧化碳
1.25
氧
1.43
氦
0.18
空气
1.29
氢
0.09
a.气体的密度表上边标明了“0℃,在标准大气压下”的条件.
b.在液体中水银的密度比较大,它大于一般金属的密度.
c.气体的密度都比较小.
注意
二、密度的应用
求质量
求体积
鉴别物质
1.求体积:
〔例1〕有一大铝勺,称其质量为540g,求它的体积是多少? (ρ铝=2.7g/cm3)
解:
(1) V=m/ ρ = 540g / 2.7g/cm3 =200cm3
〔例2〕有一卷铜线,质量是178kg,横截面积是2平方毫米,求它的长度是多少?(ρ铜=8.9g/cm3)
解:
(1) V=m/ ρ = 178kg / 8.9×103kg/m3 =2×10-2m3
(2) L=V/ s = 2×10-2m3 / 2×10-6m2 =104m
2.求质量:
〔例3〕一教室长、宽、高分别为10m、5m、4m。试求:教室内空气的质量。(ρ空=1.29kg/m3)
解:
(1) V=abc = 10m×5m×4m=200m3
(2) m= ρV = 1.29kg/m3 ×200m3 =258kg
〔例4〕 18m? 的水结成冰,体积变为多少?(ρ水=1g/cm3)(ρ冰=0.9g/cm3)
对应关系:
解:
(1) m1= ρ1V1 = 1 ×103kg/m3 ×18m3 =1.8 ×104kg
V2=m2/ ρ2 = 1.8 ×104kg / 0.9×103kg/m3
=20m3
〔例5〕一奖牌质量为45g,测得其体积为5cm3,请判断它是否由纯金制成。(ρ金=19.3g/cm3)
3.求密度:
解:
(1) ρ=m/ V= 45 g / 5 cm3 =9 g/cm3
〔例6〕有一花岗岩石碑,其体积为20立方米,为了计算其质量,有人找了一小块同种花岗岩样品,测得该样品的质量为14g,体积为5立方厘米,。利用这些数据,请你算出花岗岩碑石的质量是多少?
解:
(1) ρ1=m1/ V1= 14 g / 5 cm3 =2.8 g/cm3 = 2.8 ×103kg/m3
(2) m2= ρ2V2= 2.8 ×103kg/m3 ×20m3 =5.6 ×104kg
〔例7〕有一个体积是40cm3的铜球,它的质量是267g,这个铜球是空心的还是实心的? 如果是空心的,求空心的体积是多少? (ρ铜=8.9g/cm3)
解:
(1) ρ=m/ V= 267 g / 40cm3 =6.7 g/cm3
(2) m= ρV= 8.9 g/cm3 ×40cm3 =356g
(3) V=m/ ρ = 267g / 8.9g/cm3 =30cm3
V空= 40cm3 - 30cm3 = 10cm3
〔例8〕以用油罐车来运输,它的密度是0.8×10?kg/m? .如果每节油罐车的容量是80m? ,运输800t石油需多少节油罐车?
解:
(1) m0= ρV= 0.8×103kg/m3 ×80m3 =6.4 ×104kg=64 t
N=m/m0=800t/64t=12.5节=13节
(2) V0=m/ ρ = 8×105kg/ 0.8×103kg/m3 =103m3
N=V/V0= 103m3 / 80m3 =12.5节=13节
练习:
〔例9〕一烧杯空烧杯的质量为500g,装满水后,总质量是700g,装满某种液体后总质量是860g,求该液体的密度。
解:
(1) V1=m1/ ρ 1= 200g / 1g/cm3 =200cm3
(2) ρ2=m2/ V2= 360 g / 200cm3 =1.8g/cm3
〔例10〕 “乌鸦喝水”的故事你不陌生吧.如图所示,若有一只容积为3×10 -4 m 3 的瓶内盛有0.2kg的水,一只口渴的乌鸦每次将一块质量为10g的小石子投入瓶中,当乌鸦投入了25块相同的小石子后,水面升到了瓶口.求:(1)瓶内石块的总体积;(2)瓶内石块的密度.
解:
(1) V1=m1/ ρ 1= 200g / 1g/cm3 =200cm3
V石=V瓶-V1=300cm3-200cm3=100cm3
(2) ρ2=m2/ V2= 250 g / 100cm3 =2.5g/cm3
〔例11〕一块石块的质量为50g将放入装满水的溢水杯中,溢出水的质量为20g,求⑴石块的密度,⑵将它放入装满酒精的溢水杯中,溢出酒精的质量为多少克(已知酒精的密度是0.8X103kg/m3)
解:
(1)V=m1/ ρ1 = 20g / 1g/cm3 =20cm3
ρ2=m2/ V= 50 g / 20cm3 =2.5 g/cm3
m3= ρ3V3 = 0.8g/cm3 ×20cm3 =16g
〔例12〕为了用铁浇铸一个机器零件,先用蜡做了一个该零件的模型,已知该模型质量为1800g,蜡的密度为0.9×1?03kg/m3,那么浇铸这样一个铁件需要多少kg铁?(ρ铁=7.9×103kg/m3)
解:
(1) V1=m1/ ρ 1= 1800g / 0.9g/cm3 =2000cm3
(2)m2 =ρ2V2= 7.9g/cm3 ×2000cm3 =15.8kg
总结:
密度问题三种隐含条件:
1.密度相等(同种物质)
2.质量相等(水结冰)
3.体积相等(石块排水、容器盛物、模和零件)
设计
课题
预备
实验
10
5
论证
口诀
练习
拓展
挑战
返回
结束
应用
怎样鉴别戒指是不是纯金的?
怎样知道矿石是什么物质的?
怎样知道一大卷细铜丝的长度?
?
矗立在天安门广场的人民英雄纪念碑,它的碑心石是一整块巨大的花岗岩,碑身高37.94m,由413块花岗岩石块砌成,在长14.7m、宽2.9m、厚1m的碑心石上刻着“人民英雄永垂不朽”.怎样知道它的质量?
由于密度的知识很有用,科学家们测出了各种物质的密度,供大家使用.
物质名称
密度
物质名称
密度
锇
铝
金
花岗岩
铅
砖
银
冰
铜
蜡
钢、铁
干松木
一些固体的密度
一些液体的密度
物质名称
密度
物质名称
密度
水银
植物油
硫酸
煤油
海水
酒精
纯水
汽油
一些气体的密度(0℃ ,在标准大气压下)
物质名称
密度
物质名称
密度
二氧化碳
1.98
一氧化碳
1.25
氧
1.43
氦
0.18
空气
1.29
氢
0.09
a.气体的密度表上边标明了“0℃,在标准大气压下”的条件.
b.在液体中水银的密度比较大,它大于一般金属的密度.
c.气体的密度都比较小.
注意
二、密度的应用
求质量
求体积
鉴别物质
1.求体积:
〔例1〕有一大铝勺,称其质量为540g,求它的体积是多少? (ρ铝=2.7g/cm3)
解:
(1) V=m/ ρ = 540g / 2.7g/cm3 =200cm3
〔例2〕有一卷铜线,质量是178kg,横截面积是2平方毫米,求它的长度是多少?(ρ铜=8.9g/cm3)
解:
(1) V=m/ ρ = 178kg / 8.9×103kg/m3 =2×10-2m3
(2) L=V/ s = 2×10-2m3 / 2×10-6m2 =104m
2.求质量:
〔例3〕一教室长、宽、高分别为10m、5m、4m。试求:教室内空气的质量。(ρ空=1.29kg/m3)
解:
(1) V=abc = 10m×5m×4m=200m3
(2) m= ρV = 1.29kg/m3 ×200m3 =258kg
〔例4〕 18m? 的水结成冰,体积变为多少?(ρ水=1g/cm3)(ρ冰=0.9g/cm3)
对应关系:
解:
(1) m1= ρ1V1 = 1 ×103kg/m3 ×18m3 =1.8 ×104kg
V2=m2/ ρ2 = 1.8 ×104kg / 0.9×103kg/m3
=20m3
〔例5〕一奖牌质量为45g,测得其体积为5cm3,请判断它是否由纯金制成。(ρ金=19.3g/cm3)
3.求密度:
解:
(1) ρ=m/ V= 45 g / 5 cm3 =9 g/cm3
〔例6〕有一花岗岩石碑,其体积为20立方米,为了计算其质量,有人找了一小块同种花岗岩样品,测得该样品的质量为14g,体积为5立方厘米,。利用这些数据,请你算出花岗岩碑石的质量是多少?
解:
(1) ρ1=m1/ V1= 14 g / 5 cm3 =2.8 g/cm3 = 2.8 ×103kg/m3
(2) m2= ρ2V2= 2.8 ×103kg/m3 ×20m3 =5.6 ×104kg
〔例7〕有一个体积是40cm3的铜球,它的质量是267g,这个铜球是空心的还是实心的? 如果是空心的,求空心的体积是多少? (ρ铜=8.9g/cm3)
解:
(1) ρ=m/ V= 267 g / 40cm3 =6.7 g/cm3
(2) m= ρV= 8.9 g/cm3 ×40cm3 =356g
(3) V=m/ ρ = 267g / 8.9g/cm3 =30cm3
V空= 40cm3 - 30cm3 = 10cm3
〔例8〕以用油罐车来运输,它的密度是0.8×10?kg/m? .如果每节油罐车的容量是80m? ,运输800t石油需多少节油罐车?
解:
(1) m0= ρV= 0.8×103kg/m3 ×80m3 =6.4 ×104kg=64 t
N=m/m0=800t/64t=12.5节=13节
(2) V0=m/ ρ = 8×105kg/ 0.8×103kg/m3 =103m3
N=V/V0= 103m3 / 80m3 =12.5节=13节
练习:
〔例9〕一烧杯空烧杯的质量为500g,装满水后,总质量是700g,装满某种液体后总质量是860g,求该液体的密度。
解:
(1) V1=m1/ ρ 1= 200g / 1g/cm3 =200cm3
(2) ρ2=m2/ V2= 360 g / 200cm3 =1.8g/cm3
〔例10〕 “乌鸦喝水”的故事你不陌生吧.如图所示,若有一只容积为3×10 -4 m 3 的瓶内盛有0.2kg的水,一只口渴的乌鸦每次将一块质量为10g的小石子投入瓶中,当乌鸦投入了25块相同的小石子后,水面升到了瓶口.求:(1)瓶内石块的总体积;(2)瓶内石块的密度.
解:
(1) V1=m1/ ρ 1= 200g / 1g/cm3 =200cm3
V石=V瓶-V1=300cm3-200cm3=100cm3
(2) ρ2=m2/ V2= 250 g / 100cm3 =2.5g/cm3
〔例11〕一块石块的质量为50g将放入装满水的溢水杯中,溢出水的质量为20g,求⑴石块的密度,⑵将它放入装满酒精的溢水杯中,溢出酒精的质量为多少克(已知酒精的密度是0.8X103kg/m3)
解:
(1)V=m1/ ρ1 = 20g / 1g/cm3 =20cm3
ρ2=m2/ V= 50 g / 20cm3 =2.5 g/cm3
m3= ρ3V3 = 0.8g/cm3 ×20cm3 =16g
〔例12〕为了用铁浇铸一个机器零件,先用蜡做了一个该零件的模型,已知该模型质量为1800g,蜡的密度为0.9×1?03kg/m3,那么浇铸这样一个铁件需要多少kg铁?(ρ铁=7.9×103kg/m3)
解:
(1) V1=m1/ ρ 1= 1800g / 0.9g/cm3 =2000cm3
(2)m2 =ρ2V2= 7.9g/cm3 ×2000cm3 =15.8kg
总结:
密度问题三种隐含条件:
1.密度相等(同种物质)
2.质量相等(水结冰)
3.体积相等(石块排水、容器盛物、模和零件)
设计
课题
预备
实验
10
5
论证
口诀
练习
拓展
挑战
返回
结束
应用
同课章节目录
- 第一章 打开物理世界的大门
- 第一节 走进神奇
- 第二节 探索之路
- 第三节 站在巨人的肩膀上
- 第二章 运动的世界
- 第一节 动与静
- 第二节 长度与时间的测量
- 第三节 快与慢
- 第四节 科学探究:速度的变化
- 第三章 声的世界
- 第一节 科学探究:声音的产生与传播
- 第二节 声音的特性
- 第三节 超声与次声
- 第四章 多彩的光
- 第一节 光的反射
- 第二节 平面镜成像
- 第三节 光的折射
- 第四节 光的色散
- 第五节 科学探究:凸透镜成像
- 第六节 神奇的眼睛
- 第五章 质量与密度
- 第一节 质量
- 第二节 学习使用天平和量筒
- 第三节 科学探究:物质的密度
- 第四节 密度知识的应用
- 第六章 熟悉而陌生的力
- 第一节 力
- 第二节 怎样描述力
- 第三节 弹力与弹簧测力计
- 第四节 来自地球的力
- 第五节 科学探究:摩擦力
- 第七章 力与运动
- 第一节 科学探究:牛顿第一定律
- 第二节 力的合成
- 第三节 力的平衡
- 第八章 压强
- 第一节 压力的作用效果
- 第二节 科学探究:液体的压强
- 第三节 空气的“力量”
- 第四节 流体压强与流速的关系
- 第九章 浮力
- 第一节 认识浮力
- 第二节 阿基米德原理
- 第三节 物体的浮与沉
- 第十章 机械与人
- 第一节 科学探究:杠杆的平衡条件
- 第二节 滑轮及其应用
- 第三节 做功了吗
- 第四节 做功的快慢
- 第五节 机械效率
- 第六节 合理利用机械能
- 第十一章 小粒子与大宇宙
- 第一节 走进微观
- 第二节 看不见的运动
- 第三节 探索宇宙
