2020-2021学年苏科版八年级下册数学《第9章 中心对称图形——平行四边形》单元测试卷(Word版 有解析)
文档属性
| 名称 | 2020-2021学年苏科版八年级下册数学《第9章 中心对称图形——平行四边形》单元测试卷(Word版 有解析) |  | |
| 格式 | zip | ||
| 文件大小 | 224.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-19 23:40:21 | ||
图片预览


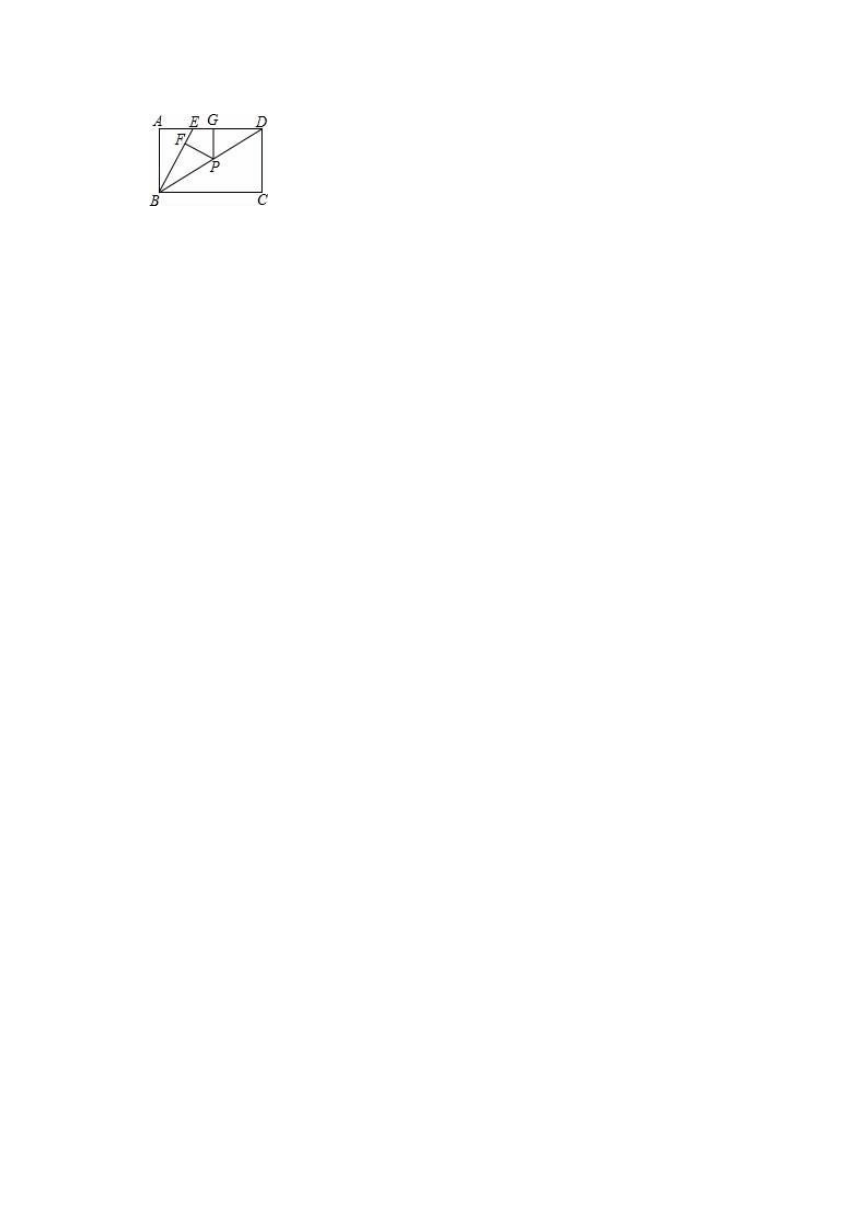
文档简介
2020-2021学年苏科新版八年级下册数学《第9章
中心对称图形——平行四边形》单元测试卷
一.选择题
1.如图是日本“三菱”汽车的标志,它可以看作是由菱形通过旋转得到的,每次旋转了( )
A.60°
B.90°
C.120°
D.150°
2.下列图形中,( )旋转90°后能与自身重合.
A.
B.
C.
D.
3.如图,△ABC与△A′B′C′成中心对称,则下列说法不正确的是( )
A.S△ACB=
B.AB=A′B′
C.AB∥A′B′,A′C′∥AC,BC∥B′C′
D.=S△ACO
4.以不在一条直线上的三点A、B、C为顶点的平行四边形共有( )
A.1个
B.2个
C.3个
D.4个
5.如图所示,在?ABCD中,EF∥GH∥AB,MN∥BC,则图中的平行四边形的个数为( )
A.12个
B.16个
C.14个
D.18个
6.在下列图形中,既是中心对称图形,又是轴对称图形的个数是( )
①线段;②角;③正方形;④长方形;⑤等腰三角形;⑥直角三角形.
A.1个
B.2个
C.3个
D.4个
7.如图,五边形ABCDE中,∠ABC=∠AED=90°,AB=CD=AE=BC+DE=1,则这个五边形ABCDE的面积等于( )
A.1
B.2
C.3
D.4
8.正方形和等腰三角形有相等的周长,等腰三角形两边长分别为5.6cm和13.2cm,则这个正方形的面积为( )
A.64cm2
B.48cm2
C.36cm2
D.24cm2
9.梯形的一腰长为10cm,这腰和底边所成的角为30°,中位线长12cm,则此梯形的面积为( )
A.30cm2
B.40cm2
C.50cm2
D.60cm2
10.在?ABCD中,若∠A+∠C=120°,则∠C的度数是( )
A.120°
B.30°
C.60°
D.90°
二.填空题
11.连接两个成中心对称图形的两个对称点的线段的中点是这两个图形的
.
12.把一个图形绕着一个定点旋转一个角度α后,与初始图形重合,这种图形叫做
,这个定点叫做
,旋转的角度叫做
,其取值范围是
(用α表示).
13.梯形中位线长18cm,被一条对角线分成两段,这两段差为4cm,则梯形两底的长为
.
14.对角线
的矩形是正方形.
15.如图所示,如果要使一个平行四边形成为一个矩形,需要添加一个条件是
度.
16.一组对边平行且相等的四边形一定是
形.
17.如图,在△ABC中,D是AB上一点,AD=AC,AE⊥CD,垂足为点E,F是BC的中点,若BD=16,则EF的长为
.
18.如图,正方形ABCD的边长为8,E为边AD上一点.若BE=10,则CE=
.
19.如图,已知四边形ABCD是一个平行四边形,则只须补充条件
,就可以判定它是一个菱形.
20.在△ABC中,D为AB的中点,且CD=AD=BD,那么∠ACB=
度.
三.解答题
21.如图,在△ABC中,∠B=2∠C,AD⊥BC于D,M为BC的中点,求证:DM=AB.
22.在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D.BE⊥MN于点E.
(1)当直线MN绕点C旋转到如图所示位置时,求证:DE=AD+BE;
(2)当直线MN绕点C旋转到与线段AB相交(交点不是AB中点)时,画出相应的图形,探求线段DE,AD与BE之间的等量关系,并写出其关系式.
23.如图,线段AC、BD相交于点O,且AB∥CD,AB=CD,此图形是中心对称图形吗?试说明你的理由.
24.如图,△ACD、△ABE、△BCF均为直线BC同侧的等边三角形.当AB≠AC时,求证:四边形ADFE为平行四边形.
25.如图,在平行四边形ABCD中,∠DAB=60°,点E,F分别在CD,AB的延长线上,且AE=AD,CF=CB.求证:四边形AFCE是平行四边形.
26.平行四边形ABCD的两条对角线AC、BD相交于点O,AB=,AO=2,OB=1.四边形ABCD是菱形吗?为什么?
27.如图,E是矩形ABCD的边AD上一点,且BE=ED,P是对角线BD上任意一点,PF⊥BE,PG⊥AD,垂足分别为F、G.求证:PF+PG=AB.
参考答案与试题解析
一.选择题
1.解:每次旋转的度数为:360°÷3=120°.
故选:C.
2.解:第一个图形旋转的最小度数是60度,错误;
第二个图形旋转的最小角度是60度,错误;
第三个图形的旋转的最小的度数是90度,正确;
第四个图形的旋转的最小的度数是72°,错误.
故选:C.
3.解:A、根据中心对称的两个图形全等,即可得到,故本选项正确;
B、成中心对称的两图形全等,对应线段相等,故本选项正确;
C、根据对称点到对称中心的距离相等,即可证得对应线段平行,故本选项正确;
D、=S△ABO≠S△ACO,本选项错误.
故选:D.
4.解:如图以点A,B,C为顶点能做三个平行四边形:?ABCD,?ABFC,?AEBC.
故选:C.
5.解:根据平行四边形的定义:两组对边分别平行的四边形是平行四边形,则图中的四边形AEOM、AEFB、AMND、CNOF、CNMB、CDEF、DNOE、BMOF、AGPM、GPND、MPHB、HPCN、OEGP、OPHF、EGHF、GHCD、AGHB和ABCD都是平行四边形,共18个.
故选:D.
6.解:①线段是轴对称图形,也是中心对称图形;
②角是轴对称图形,不是中心对称图形;
③正方形是轴对称图形,也是中心对称图形;
④长方形是轴对称图形,也是中心对称图形;
⑤等腰三角形是轴对称图形,不是中心对称图形;
⑥直角三角形不一定是轴对称图形,也不一定是中心对称图形.
故选:C.
7.解:连接AC、AD,
∵∠ABC+∠ABD′=180°,
∴C、B、D′三点共线,
∴△ABD′≌△ABC,即△AED≌△ABC,
∴S△ACD′=×1×1=,
∵△ACD′≌△ACD(SSS),
∴S△ACD=,
∴这个五边形ABCDE的面积等于1.
故选:A.
8.解:∵等腰三角形两边长分别为5.6cm和13.2cm,且5.6×2<13.2,
∴等腰三角形的周长=13.2×2+5.6=32cm,
∵正方形和等腰三角形有相等的周长,
∴正方形的边长==8cm,
∴正方形的面积=64cm2,
故选:A.
9.解:由梯形的一腰长为10cm,这腰和底边所成的角为30°,可得梯形的高为5;
又因为梯形的中位线长12cm,则此梯形的面积为12×5=60(cm2).故选D.
10.解:∵四边形ABCD是平行四边形,
∴∠A=∠C,
∵∠A+∠C=120°,
∴∠C=60°,
故选:C.
二.填空题
11.解:连接两个成中心对称图形的两个对称点的线段的中点是这两个图形的对称中心,
故答案为:对称中心.
12.解:把一个图形绕着一个定点旋转一个角度α后,与初始图形重合,这种图形叫做旋转对称图形,这个定点叫做旋转对称中心,旋转的角度叫做旋转角,其取值范围是0°<α<360°.
故答案为:旋转对称图形;旋转对称中心;旋转角;0°<α<360°.
13.解:设梯形的一条对角线把中位线分成两条线段中长的线段为xcm,短的为ycm.
则x+y=18,
因为x﹣y=4,
求解方程组得,x=11,y=7,
由三角形的中位线性质可得,上底长为2×7=14cm,下底长为2×12=22cm,
故答案为14cm,22cm.
14.解:对角线互相垂直的矩形是正方形.故答案为:互相垂直.
15.解:∵一个角是90度的平行四边形是矩形
∴添加∠A=90.
16.解:一组对边平行且相等的四边形一定是平行四边形.
故答案为:平行四边.
17.解:∵AD=AC,AE⊥CD,
∴E为CD的中点,
又∵F是CB的中点,
∴EF为△BCD的中位线,
∴EF∥BD,EF=BD,
∵BD=16,
∴EF=8,
故答案为:8.
18.解:∵四边形ABCD是正方形,
∴∠A=∠D=90°,AB=CD=AD=8,
∴AE===6,
∴DE=AD﹣AE=2,
∴CE===2;
故答案为:2.
19.解:补充的条件是AB=BC,
理由是:∵AB=BC,四边形ABCD是平行四边形,
∴平行四边形ABCD是菱形,
故答案为:AB=BC.
20.解:已知D为AB的中点,即CD为AB边的中线,CD=AD=BD=AB,因为直角三角形的斜边上的中线等于斜边的一半,则∠ACB=90°,故填90.
三.解答题
21.证明:取AC的中点N,连接MN,DN,
∵M为BC的中点,
∴MN为△ABC的中位线,
∴MN∥AB,且MN=AB,
∴∠B=∠NMC,又∠B=2∠C,
∴∠NMC=2∠C,
∵∠NMC为△DMN的外角,
∴∠NMC=∠MDN+∠MND=2∠C,
又DN为Rt△ADC斜边上的中线,
∴DN=NC=AN=AC,
∴∠MDN=∠C,
∴∠MND=∠C=∠MDN,
∴DM=MN,
则DM=AB.
22.(1)证明:如图1,
∵AD⊥MN于点D.BE⊥MN于点E,
∴∠ADC=90°,∠CEB=90°,
∵∠ACB=90°,
∴∠ACD=∠CBE,
在△ACD和△CBE中,
,
∴△ACD≌△CBE(AAS),
∴AD=CE,CD=BE,
∴DE=CE+CD=AD+BE;
(2)如图2,DE=AD﹣BE;
如图3,DE=BE﹣AD.
23.解:是中心对称图形,
∵AB∥CD,
∴∠A=∠C,∠B=∠D,
在△AOB与△COD中,
,
∴△AOB≌△COD(ASA),
∴OA=OC,OB=OD.
∴此图形是中心对称图形.
24.证明:
∵△ABE、△BCF为等边三角形,
∴AB=BE=AE,BC=CF=FB,∠ABE=∠CBF=60°.
∴∠FBE=∠CBA,
在△FBE和△CBA中,
,
∴△FBE≌△CBA(SAS).
∴EF=AC.
又∵△ADC为等边三角形,
∴CD=AD=AC.
∴EF=AD.
同理可得AE=DF.
∴四边形AEFD是平行四边形.
25.证明:∵AE=AD,CF=CB,
∴∠E=∠ADE,∠CBF=∠F.
在?ABCD中,∠ADC=∠ABC,
∴∠ADE=∠CBF.
∴∠E=∠F.
在?ABCD中,CD∥AB,
∴∠E+∠EAF=180°,
∴∠F+∠EAF=180°.
∴AE∥CF.
又∵CE∥AF,
∴四边形AFCE是平行四边形.
26.解:在△AOB中,
∵AB=,AO=2,OB=1,
∴AB2=()2=5,AO2+OB2=22+12=5,
∴AB2=AO2+OB2,
∴△AOB为直角三角形,即∠AOB=90°.
∴AC、BD互相垂直.
∴四边形ABCD是菱形(对角线互相垂直的平行四边形是菱形).
27.证明:连接PE,∵BE=ED,PF⊥BE,PG⊥AD,
∴S△BDE=S△BEP+S△DEP
=BE?PF+ED?PG
=ED?(PF+PG),
又∵四边形ABCD是矩形,
∴BA⊥AD,
∴S△BED=ED?AB,
∴ED?(PF+PG)=ED?AB,
∴PF+PG=AB.
中心对称图形——平行四边形》单元测试卷
一.选择题
1.如图是日本“三菱”汽车的标志,它可以看作是由菱形通过旋转得到的,每次旋转了( )
A.60°
B.90°
C.120°
D.150°
2.下列图形中,( )旋转90°后能与自身重合.
A.
B.
C.
D.
3.如图,△ABC与△A′B′C′成中心对称,则下列说法不正确的是( )
A.S△ACB=
B.AB=A′B′
C.AB∥A′B′,A′C′∥AC,BC∥B′C′
D.=S△ACO
4.以不在一条直线上的三点A、B、C为顶点的平行四边形共有( )
A.1个
B.2个
C.3个
D.4个
5.如图所示,在?ABCD中,EF∥GH∥AB,MN∥BC,则图中的平行四边形的个数为( )
A.12个
B.16个
C.14个
D.18个
6.在下列图形中,既是中心对称图形,又是轴对称图形的个数是( )
①线段;②角;③正方形;④长方形;⑤等腰三角形;⑥直角三角形.
A.1个
B.2个
C.3个
D.4个
7.如图,五边形ABCDE中,∠ABC=∠AED=90°,AB=CD=AE=BC+DE=1,则这个五边形ABCDE的面积等于( )
A.1
B.2
C.3
D.4
8.正方形和等腰三角形有相等的周长,等腰三角形两边长分别为5.6cm和13.2cm,则这个正方形的面积为( )
A.64cm2
B.48cm2
C.36cm2
D.24cm2
9.梯形的一腰长为10cm,这腰和底边所成的角为30°,中位线长12cm,则此梯形的面积为( )
A.30cm2
B.40cm2
C.50cm2
D.60cm2
10.在?ABCD中,若∠A+∠C=120°,则∠C的度数是( )
A.120°
B.30°
C.60°
D.90°
二.填空题
11.连接两个成中心对称图形的两个对称点的线段的中点是这两个图形的
.
12.把一个图形绕着一个定点旋转一个角度α后,与初始图形重合,这种图形叫做
,这个定点叫做
,旋转的角度叫做
,其取值范围是
(用α表示).
13.梯形中位线长18cm,被一条对角线分成两段,这两段差为4cm,则梯形两底的长为
.
14.对角线
的矩形是正方形.
15.如图所示,如果要使一个平行四边形成为一个矩形,需要添加一个条件是
度.
16.一组对边平行且相等的四边形一定是
形.
17.如图,在△ABC中,D是AB上一点,AD=AC,AE⊥CD,垂足为点E,F是BC的中点,若BD=16,则EF的长为
.
18.如图,正方形ABCD的边长为8,E为边AD上一点.若BE=10,则CE=
.
19.如图,已知四边形ABCD是一个平行四边形,则只须补充条件
,就可以判定它是一个菱形.
20.在△ABC中,D为AB的中点,且CD=AD=BD,那么∠ACB=
度.
三.解答题
21.如图,在△ABC中,∠B=2∠C,AD⊥BC于D,M为BC的中点,求证:DM=AB.
22.在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D.BE⊥MN于点E.
(1)当直线MN绕点C旋转到如图所示位置时,求证:DE=AD+BE;
(2)当直线MN绕点C旋转到与线段AB相交(交点不是AB中点)时,画出相应的图形,探求线段DE,AD与BE之间的等量关系,并写出其关系式.
23.如图,线段AC、BD相交于点O,且AB∥CD,AB=CD,此图形是中心对称图形吗?试说明你的理由.
24.如图,△ACD、△ABE、△BCF均为直线BC同侧的等边三角形.当AB≠AC时,求证:四边形ADFE为平行四边形.
25.如图,在平行四边形ABCD中,∠DAB=60°,点E,F分别在CD,AB的延长线上,且AE=AD,CF=CB.求证:四边形AFCE是平行四边形.
26.平行四边形ABCD的两条对角线AC、BD相交于点O,AB=,AO=2,OB=1.四边形ABCD是菱形吗?为什么?
27.如图,E是矩形ABCD的边AD上一点,且BE=ED,P是对角线BD上任意一点,PF⊥BE,PG⊥AD,垂足分别为F、G.求证:PF+PG=AB.
参考答案与试题解析
一.选择题
1.解:每次旋转的度数为:360°÷3=120°.
故选:C.
2.解:第一个图形旋转的最小度数是60度,错误;
第二个图形旋转的最小角度是60度,错误;
第三个图形的旋转的最小的度数是90度,正确;
第四个图形的旋转的最小的度数是72°,错误.
故选:C.
3.解:A、根据中心对称的两个图形全等,即可得到,故本选项正确;
B、成中心对称的两图形全等,对应线段相等,故本选项正确;
C、根据对称点到对称中心的距离相等,即可证得对应线段平行,故本选项正确;
D、=S△ABO≠S△ACO,本选项错误.
故选:D.
4.解:如图以点A,B,C为顶点能做三个平行四边形:?ABCD,?ABFC,?AEBC.
故选:C.
5.解:根据平行四边形的定义:两组对边分别平行的四边形是平行四边形,则图中的四边形AEOM、AEFB、AMND、CNOF、CNMB、CDEF、DNOE、BMOF、AGPM、GPND、MPHB、HPCN、OEGP、OPHF、EGHF、GHCD、AGHB和ABCD都是平行四边形,共18个.
故选:D.
6.解:①线段是轴对称图形,也是中心对称图形;
②角是轴对称图形,不是中心对称图形;
③正方形是轴对称图形,也是中心对称图形;
④长方形是轴对称图形,也是中心对称图形;
⑤等腰三角形是轴对称图形,不是中心对称图形;
⑥直角三角形不一定是轴对称图形,也不一定是中心对称图形.
故选:C.
7.解:连接AC、AD,
∵∠ABC+∠ABD′=180°,
∴C、B、D′三点共线,
∴△ABD′≌△ABC,即△AED≌△ABC,
∴S△ACD′=×1×1=,
∵△ACD′≌△ACD(SSS),
∴S△ACD=,
∴这个五边形ABCDE的面积等于1.
故选:A.
8.解:∵等腰三角形两边长分别为5.6cm和13.2cm,且5.6×2<13.2,
∴等腰三角形的周长=13.2×2+5.6=32cm,
∵正方形和等腰三角形有相等的周长,
∴正方形的边长==8cm,
∴正方形的面积=64cm2,
故选:A.
9.解:由梯形的一腰长为10cm,这腰和底边所成的角为30°,可得梯形的高为5;
又因为梯形的中位线长12cm,则此梯形的面积为12×5=60(cm2).故选D.
10.解:∵四边形ABCD是平行四边形,
∴∠A=∠C,
∵∠A+∠C=120°,
∴∠C=60°,
故选:C.
二.填空题
11.解:连接两个成中心对称图形的两个对称点的线段的中点是这两个图形的对称中心,
故答案为:对称中心.
12.解:把一个图形绕着一个定点旋转一个角度α后,与初始图形重合,这种图形叫做旋转对称图形,这个定点叫做旋转对称中心,旋转的角度叫做旋转角,其取值范围是0°<α<360°.
故答案为:旋转对称图形;旋转对称中心;旋转角;0°<α<360°.
13.解:设梯形的一条对角线把中位线分成两条线段中长的线段为xcm,短的为ycm.
则x+y=18,
因为x﹣y=4,
求解方程组得,x=11,y=7,
由三角形的中位线性质可得,上底长为2×7=14cm,下底长为2×12=22cm,
故答案为14cm,22cm.
14.解:对角线互相垂直的矩形是正方形.故答案为:互相垂直.
15.解:∵一个角是90度的平行四边形是矩形
∴添加∠A=90.
16.解:一组对边平行且相等的四边形一定是平行四边形.
故答案为:平行四边.
17.解:∵AD=AC,AE⊥CD,
∴E为CD的中点,
又∵F是CB的中点,
∴EF为△BCD的中位线,
∴EF∥BD,EF=BD,
∵BD=16,
∴EF=8,
故答案为:8.
18.解:∵四边形ABCD是正方形,
∴∠A=∠D=90°,AB=CD=AD=8,
∴AE===6,
∴DE=AD﹣AE=2,
∴CE===2;
故答案为:2.
19.解:补充的条件是AB=BC,
理由是:∵AB=BC,四边形ABCD是平行四边形,
∴平行四边形ABCD是菱形,
故答案为:AB=BC.
20.解:已知D为AB的中点,即CD为AB边的中线,CD=AD=BD=AB,因为直角三角形的斜边上的中线等于斜边的一半,则∠ACB=90°,故填90.
三.解答题
21.证明:取AC的中点N,连接MN,DN,
∵M为BC的中点,
∴MN为△ABC的中位线,
∴MN∥AB,且MN=AB,
∴∠B=∠NMC,又∠B=2∠C,
∴∠NMC=2∠C,
∵∠NMC为△DMN的外角,
∴∠NMC=∠MDN+∠MND=2∠C,
又DN为Rt△ADC斜边上的中线,
∴DN=NC=AN=AC,
∴∠MDN=∠C,
∴∠MND=∠C=∠MDN,
∴DM=MN,
则DM=AB.
22.(1)证明:如图1,
∵AD⊥MN于点D.BE⊥MN于点E,
∴∠ADC=90°,∠CEB=90°,
∵∠ACB=90°,
∴∠ACD=∠CBE,
在△ACD和△CBE中,
,
∴△ACD≌△CBE(AAS),
∴AD=CE,CD=BE,
∴DE=CE+CD=AD+BE;
(2)如图2,DE=AD﹣BE;
如图3,DE=BE﹣AD.
23.解:是中心对称图形,
∵AB∥CD,
∴∠A=∠C,∠B=∠D,
在△AOB与△COD中,
,
∴△AOB≌△COD(ASA),
∴OA=OC,OB=OD.
∴此图形是中心对称图形.
24.证明:
∵△ABE、△BCF为等边三角形,
∴AB=BE=AE,BC=CF=FB,∠ABE=∠CBF=60°.
∴∠FBE=∠CBA,
在△FBE和△CBA中,
,
∴△FBE≌△CBA(SAS).
∴EF=AC.
又∵△ADC为等边三角形,
∴CD=AD=AC.
∴EF=AD.
同理可得AE=DF.
∴四边形AEFD是平行四边形.
25.证明:∵AE=AD,CF=CB,
∴∠E=∠ADE,∠CBF=∠F.
在?ABCD中,∠ADC=∠ABC,
∴∠ADE=∠CBF.
∴∠E=∠F.
在?ABCD中,CD∥AB,
∴∠E+∠EAF=180°,
∴∠F+∠EAF=180°.
∴AE∥CF.
又∵CE∥AF,
∴四边形AFCE是平行四边形.
26.解:在△AOB中,
∵AB=,AO=2,OB=1,
∴AB2=()2=5,AO2+OB2=22+12=5,
∴AB2=AO2+OB2,
∴△AOB为直角三角形,即∠AOB=90°.
∴AC、BD互相垂直.
∴四边形ABCD是菱形(对角线互相垂直的平行四边形是菱形).
27.证明:连接PE,∵BE=ED,PF⊥BE,PG⊥AD,
∴S△BDE=S△BEP+S△DEP
=BE?PF+ED?PG
=ED?(PF+PG),
又∵四边形ABCD是矩形,
∴BA⊥AD,
∴S△BED=ED?AB,
∴ED?(PF+PG)=ED?AB,
∴PF+PG=AB.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
