2020-2021学年苏科新版九年级下册数学《第6章 图形的相似》单元测试卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年苏科新版九年级下册数学《第6章 图形的相似》单元测试卷(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 354.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-19 23:43:02 | ||
图片预览




文档简介
2020-2021学年苏科新版九年级下册数学《第6章
图形的相似》单元测试卷
一.选择题
1.如图,梯形ABCD中,AB∥CD∥EF,若AB=10,CD=3,EF=5,则CF:FB等于( )
A.2:7
B.5:7
C.3:7
D.2:5
2.下列两个三角形不一定相似的是( )
A.两个等边三角形
B.两个全等三角形
C.两个直角三角形
D.两个等腰直角三角形
3.某校计划在一块三角形的空地上修建一个面积最大的正方形水池,使得水池的一边在△ABC的边BC上,△ABC中边BC=60m,高AD=30m,则水池的边长应为( )
A.10m
B.20m
C.30m
D.40m
4.已知a:b:c=3:5:7,则的值为( )
A.
B.
C.
D.以上都不对
5.如图,在△ABC中,AB=AC=8,∠A=36°,BD平分∠ABC交AC于点D,则AD=( )
A.4
B.4﹣4
C.﹣4+4
D.4﹣4或﹣4+4
6.语句:“①所有度数相等的角都相似;②所有边长相等的菱形都相似;③所有的正方形都相似;④所有的圆都相似”中准确的有( )
A.4句
B.3句
C.2句
D.1句
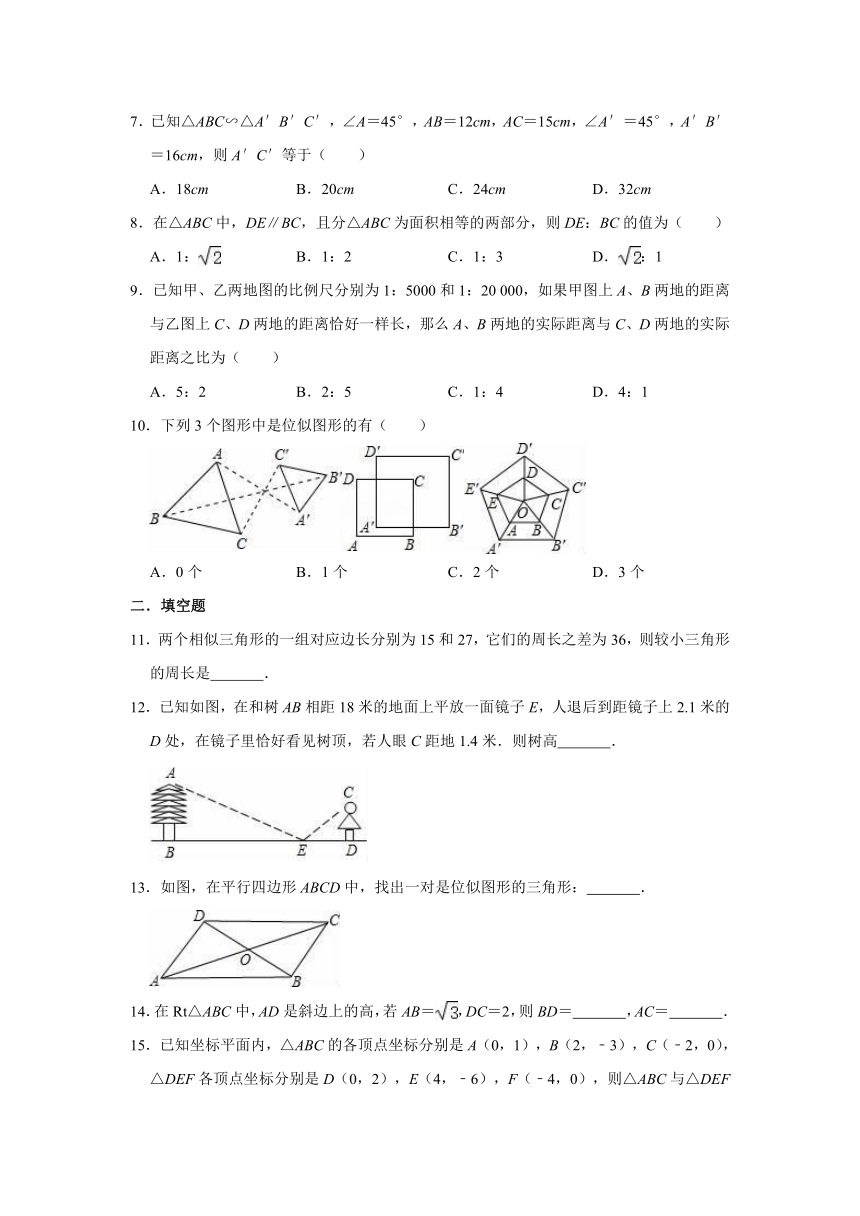
7.已知△ABC∽△A′B′C′,∠A=45°,AB=12cm,AC=15cm,∠A′=45°,A′B′=16cm,则A′C′等于( )
A.18cm
B.20cm
C.24cm
D.32cm
8.在△ABC中,DE∥BC,且分△ABC为面积相等的两部分,则DE:BC的值为( )
A.1:
B.1:2
C.1:3
D.:1
9.已知甲、乙两地图的比例尺分别为1:5000和1:20
000,如果甲图上A、B两地的距离与乙图上C、D两地的距离恰好一样长,那么A、B两地的实际距离与C、D两地的实际距离之比为( )
A.5:2
B.2:5
C.1:4
D.4:1
10.下列3个图形中是位似图形的有( )
A.0个
B.1个
C.2个
D.3个
二.填空题
11.两个相似三角形的一组对应边长分别为15和27,它们的周长之差为36,则较小三角形的周长是
.
12.已知如图,在和树AB相距18米的地面上平放一面镜子E,人退后到距镜子上2.1米的D处,在镜子里恰好看见树顶,若人眼C距地1.4米.则树高
.
13.如图,在平行四边形ABCD中,找出一对是位似图形的三角形:
.
14.在Rt△ABC中,AD是斜边上的高,若AB=,DC=2,则BD=
,AC=
.
15.已知坐标平面内,△ABC的各顶点坐标分别是A(0,1),B(2,﹣3),C(﹣2,0),△DEF各顶点坐标分别是D(0,2),E(4,﹣6),F(﹣4,0),则△ABC与△DEF的面积之比为
.
16.如图,梯形ABCD中,DC∥EF∥AB,AC交EF于G.若AE=2ED,CF=2cm,AG=5cm,则BC=
cm,CG=
cm.
17.如图,顶角为36°的等腰三角形,其底边与腰的比是k,这样的三角形叫黄金三角形,已知腰长AB=1,△ABC为第一个黄金三角形,△BCD是第二个黄金三角形,△CDE是第三个黄金三角形,以此类推,第2006个黄金三角形的周长是
.(用含k的式子表示)
18.若,则x=
.
19.若==≠0,则=
.
20.如图,在平行四边形ABCD中,AB=12cm,AD=5cm,E为AD的中点,在AB上取一点F,使△CBF∽△CDE,则AF=
cm.
三.解答题
21.以长为2的线段AB为边作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F,使PF=PD,以AF为边作正方形AMEF,点M在AD上.
(1)求AM,DM的长;
(2)求证:AM2=AD?DM;
(3)根据(2)的结论你能找出图中的黄金分割点吗?
22.判断下列两组三角形是否相似,并说明理由.
(1)△ABC和△A′B′C′都是等边三角形;
(2)△ABC中,∠C=90°,AC=BC;△A′B′C′中,∠C′=90°,A′C′=B′C′.
23.如图,PAB为⊙O的割线,P0交⊙O于点C,OP=13,PA=9,AB=7,求⊙O直径的长.
24.已知x:y:z=3:5:7,求的值.
25.已知△ABC和点O为位似中心作△ABC的位似三角形A′B′C′,并使△A′B′C′与△ABC的位似比为2:1.
26.如图,已知A、B两点的坐标分别为(40,0),(0,30),动点P从点A开始在线段AO上以每秒2个长度单位的速度向原点O运动,动直线EF从x轴开始以每秒1个单位长度的速度向上平行移动(即EF∥x轴),并且分别与y轴、线段AB交于点E、F,连接EP、FP,设动点P与动直线EF同时出发,运动时间为t秒.
(1)求t=15时,△PEF的面积;
(2)当t为何值时,△EOP与△BOA相似.
27.如图所示,已知AB∥CD∥EF,AC=CE,某同学在探索DB与DF的关系时,进行了下列探究:
由于AB∥CD,得出S△ACD=S△CBD;同理S△CED=S△CFD;
所以===;
因为AC=CE,所以BD=DF.
(1)如果AD∥CF,你发现AC、CE、BD、DF之间存在怎样的关系并说明你的猜想的正确性;
(2)利用你发现的结论,请你通过画图把已知线段MN分成2:3两部分.
参考答案与试题解析
一.选择题
1.解:过D作DG∥BC交AB于G,交EF于H.
则BG=FH=CD=3,
∴EH=EF﹣FH=2,AG=7,
∵AB∥EF,
∴EH:AG=2:7=DE:AD=CF:CB,
∴CF:FB=2:5.
故选:D.
2.解:A、相似,因为其三个角均相等,符合相似三角形的判定;
B、相似,因为全等三角形是特殊的相似三角形;
C、不相似,因为没有指明其另一锐角相等或其两直角边对应成比例;
D、相似,因为其三个角均相等,符合相似三角形的判定;
故选:C.
3.解:如图:设水池的边长为xm
∵四边形EFGH是正方形
∴EF∥BC
∴△AEF∽△ABC
∴
∴(30﹣x):30=x:60
∴x=20m
∴水池的边长应为20m.
故选:B.
4.解:由已知,得
=,=,
∴①
c=②
将①②代入,并解得
.
故选:B.
5.解:∵AB=AC=8,
∴∠ABC=∠C=(180°﹣∠A)=(180°﹣36°)=72°,
∵BD平分∠ABC,
∴∠ABD=∠CBD=∠ABC=36°,
∴∠A=∠ABD,
∴AD=BD,
∵∠BDC=∠A+∠ABD=72°,
∴∠BDC=∠C,
∴BD=BC,
∴AD=BD=BC,
∴∠A=∠CBD,∠C=∠C,
∴△ABC∽△BCD,
∴AC:BC=BC:CD,
∴AC:AD=AD:CD,
∴点D为AC的黄金分割点,
∴AD=AC=×8=4()=4.
故选:B.
6.解:①角是有公共端点的两条射线组成的图形,只有度数相等,两条射线是可以无限延长的,它们是相似形.所以①正确.
②所有菱形的四条边的比相等,但不能判断它们的对应角相等,它们不一定是相似形.所以②不正确.
③所以正方形的四个角都是90°,对应边的比都相等,它们是相似形.所以③正确.
④圆是以定点为圆心,定长为半径所组成的图形,它们只有大小不同,形状都相同,是相似形.所以④正确.
故选:B.
7.解:∵△ABC∽△A′B′C′,
∴AB:A′B′=AC:A′C′
∴12:16=15:A′C′
∴A′C′=20.
故选:B.
8.解:∵DE把△ABC为面积相等的两部分,∴△ADE的面积是△ABC面积的一半,
∵DE∥BC,
∴△ADE∽△ABC,则=,
∵△ADE的面积=AD?AE?sinA,
△ABC的面积=AB?AC?sinA,
∴=,即=,
∴DE:BC=1:.
故选:A.
9.解:把图上距离看作单位1,设A、B和C、D两地的实际距离分别为x和y,则:
1:5000=1:x,
解得x=5000,
1:20000=1:y,
解得y=20000,
∴x:y=5000:20000=1:4.
故选:C.
10.解:根据位似图形的定义可知两个图形不仅是相似图形而且每组对应点所在的直线都经过同一个点,对应边互相平行(或共线),所以位似图形的是第一个、第二个和第三个.
故选:D.
二.填空题
11.解:∵相似三角形的一组对应边长分别为15和27,
∴其相似比为15:27=5:9,
相似三角形的相似比等于对应周长的比,
可设较小的三角形的周长为5x,则另一三角形的周长为9x,
9x﹣5x=36,解得x=9,
所以较小三角形的周长为5x=45,
故答案为45.
12.解:根据题意得:∠AEB=∠CED,
∵∠ABE=∠CDE=90°,
∴△ABE∽△CDE
∴,
解得:AB=12米,
即树高12米.
故答案为12米.
13.解:若两个几何图形F与F′相似,而且对应点连线交于同一点O,则称F与F′关于点O位似,O叫做位似中心.把一个几何图形变换成与之位似的图形,叫做位似变换.因而成位似的三角形是△AOD与△COB、△AOD与△COB.故找出一对是位似图形的三角形:答案不唯一,如△AOB与△COD或△AOD与△COB.
14.解:根据射影定理可得:AB2=BD×BC;AC2=CD×BC,
∴解得:BD=1,AC=.
故答案为:1,.
15.解:∵A(0,1),B(2,﹣3),C(﹣2,0),
∴由勾股定理得:AC==,
AB==2,
BC==5,
∵D(0,2),E(4,﹣6),F(﹣4,0),
∴DE==4,
EF==10,
DF==2,
∴===,
∴△ABC∽△DEF,
∴△ABC与△DEF的面积之比是()2==1:4,
故答案为:1:4.
16.解:∵DC∥EF∥AB,
∴==2,又AG=5cm,
∴GC=2.5cm.
=,CF=2cm,
∴BC=6cm.
故答案为:6,2.5.
17.解:因为第一个黄金三角形的周长=1+1+k=2+k,
第二个黄金三角形的周长=2k+k2=k(2+k),
第三个黄金三角形的周长=2k2+k3=k2(2+k),
所以第2006个黄金三角形的周长是k2005(2+k).
故答案为k2005(2+k).
18.解:∵,
∴x2=12,
∴x=±2.
故答案为:±2.
19.解:设===k≠0,
则x=3k,y=4k,z=6k,
===.
故答案为:.
20.解:在平行四边形ABCD中,AB=12cm,AD=5cm,E为AD的中点.则BC=AD=5cm.DE=2.5cm.CD=AB=12cm.
∵△CBF∽△CDE
∴=.即=,
∴BF=
∴AF=AB﹣BF=12﹣=cm.
故答案是:.
三.解答题
21.(1)解:在Rt△APD中,PA=AB=1,AD=2,
∴PD==,
∴AM=AF=PF﹣PA=PD﹣PA=﹣1,
DM=AD﹣AM=2﹣(﹣1)=3﹣;
(2)证明:∵AM2=(﹣1)2=6﹣2,AD?DM=2(3﹣)=6﹣2,
∴AM2=AD?DM;
(3)点M是AD的黄金分割点.理由如下:
∵AM2=AD?DM,
∴═=,
∴点M是AD的黄金分割点.
22.解:(1)相似,等边三角形各角相等,各边成比例,故两这个三角形相似得到.
(2)相似,易知两三角形均为等腰直角三角形,
符合两组对应边的比相等且相应的夹角相等的两个三角形相似的判定.
23.解:延长PO到E,延长线与圆O交于点E,连接EB,AC.
∵PA=9,AB=7,
∴PB=16.
∵四边形ACEB为圆O的内接四边形,
∴∠ACP=∠E,又∠P=∠P,
∴△ACP∽△EBP,
∴=,即=,
∴=,
解得:OC=5或x=﹣5
(舍去),
则EC=2OC=10,即⊙O直径的长是10.
24.解:∵x:y:z=3:5:7,
∴设x=3k、y=5k、z=7k,
则==.
25.解:
26.解:(1)∵A、B两点的坐标分别为(40,0),(0,30),
∴OA=40,OB=30.
∵动直线EF从x轴开始以每秒1个单位长度的速度向上平行移动(即EF∥x轴),
∴t=15时,BE=30﹣15=15,
∵EF∥x轴,
∴EF是△BOA的中位线,
∴EF=OA=20,
∴S△PEF=EF?OE=×20×15=150;
(2)∵动点P从点A开始在线段AO上以每秒2个长度单位的速度向原点O运动,动直线EF从x轴开始以每秒1个单位长度的速度向上平行移动(即EF∥x轴),
∴OE=t,OP=40﹣2t,
∴当△EOP∽△BOA时,=,即=,解得t=12(秒);
当△EOP∽△AOB时,=,即=.解得t=(秒).
综上所述,当t=12秒或t=秒时,△EOP与△BOA相似.
27.解:(1)两条直线被平行线所截,对应线段成比例.即:AC:CE=BD:DF.
(2)为了把MN分成2:3两部分,从M点出发作一条射线MT,与MN有适当的夹角.
MT上取AB两点.使MA=2单位,MB=5单位,(即MA:AB=2:3).
连接NB.过A作NB的平行线,与MN相交于P.则MP:PN=2:3.
图形的相似》单元测试卷
一.选择题
1.如图,梯形ABCD中,AB∥CD∥EF,若AB=10,CD=3,EF=5,则CF:FB等于( )
A.2:7
B.5:7
C.3:7
D.2:5
2.下列两个三角形不一定相似的是( )
A.两个等边三角形
B.两个全等三角形
C.两个直角三角形
D.两个等腰直角三角形
3.某校计划在一块三角形的空地上修建一个面积最大的正方形水池,使得水池的一边在△ABC的边BC上,△ABC中边BC=60m,高AD=30m,则水池的边长应为( )
A.10m
B.20m
C.30m
D.40m
4.已知a:b:c=3:5:7,则的值为( )
A.
B.
C.
D.以上都不对
5.如图,在△ABC中,AB=AC=8,∠A=36°,BD平分∠ABC交AC于点D,则AD=( )
A.4
B.4﹣4
C.﹣4+4
D.4﹣4或﹣4+4
6.语句:“①所有度数相等的角都相似;②所有边长相等的菱形都相似;③所有的正方形都相似;④所有的圆都相似”中准确的有( )
A.4句
B.3句
C.2句
D.1句
7.已知△ABC∽△A′B′C′,∠A=45°,AB=12cm,AC=15cm,∠A′=45°,A′B′=16cm,则A′C′等于( )
A.18cm
B.20cm
C.24cm
D.32cm
8.在△ABC中,DE∥BC,且分△ABC为面积相等的两部分,则DE:BC的值为( )
A.1:
B.1:2
C.1:3
D.:1
9.已知甲、乙两地图的比例尺分别为1:5000和1:20
000,如果甲图上A、B两地的距离与乙图上C、D两地的距离恰好一样长,那么A、B两地的实际距离与C、D两地的实际距离之比为( )
A.5:2
B.2:5
C.1:4
D.4:1
10.下列3个图形中是位似图形的有( )
A.0个
B.1个
C.2个
D.3个
二.填空题
11.两个相似三角形的一组对应边长分别为15和27,它们的周长之差为36,则较小三角形的周长是
.
12.已知如图,在和树AB相距18米的地面上平放一面镜子E,人退后到距镜子上2.1米的D处,在镜子里恰好看见树顶,若人眼C距地1.4米.则树高
.
13.如图,在平行四边形ABCD中,找出一对是位似图形的三角形:
.
14.在Rt△ABC中,AD是斜边上的高,若AB=,DC=2,则BD=
,AC=
.
15.已知坐标平面内,△ABC的各顶点坐标分别是A(0,1),B(2,﹣3),C(﹣2,0),△DEF各顶点坐标分别是D(0,2),E(4,﹣6),F(﹣4,0),则△ABC与△DEF的面积之比为
.
16.如图,梯形ABCD中,DC∥EF∥AB,AC交EF于G.若AE=2ED,CF=2cm,AG=5cm,则BC=
cm,CG=
cm.
17.如图,顶角为36°的等腰三角形,其底边与腰的比是k,这样的三角形叫黄金三角形,已知腰长AB=1,△ABC为第一个黄金三角形,△BCD是第二个黄金三角形,△CDE是第三个黄金三角形,以此类推,第2006个黄金三角形的周长是
.(用含k的式子表示)
18.若,则x=
.
19.若==≠0,则=
.
20.如图,在平行四边形ABCD中,AB=12cm,AD=5cm,E为AD的中点,在AB上取一点F,使△CBF∽△CDE,则AF=
cm.
三.解答题
21.以长为2的线段AB为边作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F,使PF=PD,以AF为边作正方形AMEF,点M在AD上.
(1)求AM,DM的长;
(2)求证:AM2=AD?DM;
(3)根据(2)的结论你能找出图中的黄金分割点吗?
22.判断下列两组三角形是否相似,并说明理由.
(1)△ABC和△A′B′C′都是等边三角形;
(2)△ABC中,∠C=90°,AC=BC;△A′B′C′中,∠C′=90°,A′C′=B′C′.
23.如图,PAB为⊙O的割线,P0交⊙O于点C,OP=13,PA=9,AB=7,求⊙O直径的长.
24.已知x:y:z=3:5:7,求的值.
25.已知△ABC和点O为位似中心作△ABC的位似三角形A′B′C′,并使△A′B′C′与△ABC的位似比为2:1.
26.如图,已知A、B两点的坐标分别为(40,0),(0,30),动点P从点A开始在线段AO上以每秒2个长度单位的速度向原点O运动,动直线EF从x轴开始以每秒1个单位长度的速度向上平行移动(即EF∥x轴),并且分别与y轴、线段AB交于点E、F,连接EP、FP,设动点P与动直线EF同时出发,运动时间为t秒.
(1)求t=15时,△PEF的面积;
(2)当t为何值时,△EOP与△BOA相似.
27.如图所示,已知AB∥CD∥EF,AC=CE,某同学在探索DB与DF的关系时,进行了下列探究:
由于AB∥CD,得出S△ACD=S△CBD;同理S△CED=S△CFD;
所以===;
因为AC=CE,所以BD=DF.
(1)如果AD∥CF,你发现AC、CE、BD、DF之间存在怎样的关系并说明你的猜想的正确性;
(2)利用你发现的结论,请你通过画图把已知线段MN分成2:3两部分.
参考答案与试题解析
一.选择题
1.解:过D作DG∥BC交AB于G,交EF于H.
则BG=FH=CD=3,
∴EH=EF﹣FH=2,AG=7,
∵AB∥EF,
∴EH:AG=2:7=DE:AD=CF:CB,
∴CF:FB=2:5.
故选:D.
2.解:A、相似,因为其三个角均相等,符合相似三角形的判定;
B、相似,因为全等三角形是特殊的相似三角形;
C、不相似,因为没有指明其另一锐角相等或其两直角边对应成比例;
D、相似,因为其三个角均相等,符合相似三角形的判定;
故选:C.
3.解:如图:设水池的边长为xm
∵四边形EFGH是正方形
∴EF∥BC
∴△AEF∽△ABC
∴
∴(30﹣x):30=x:60
∴x=20m
∴水池的边长应为20m.
故选:B.
4.解:由已知,得
=,=,
∴①
c=②
将①②代入,并解得
.
故选:B.
5.解:∵AB=AC=8,
∴∠ABC=∠C=(180°﹣∠A)=(180°﹣36°)=72°,
∵BD平分∠ABC,
∴∠ABD=∠CBD=∠ABC=36°,
∴∠A=∠ABD,
∴AD=BD,
∵∠BDC=∠A+∠ABD=72°,
∴∠BDC=∠C,
∴BD=BC,
∴AD=BD=BC,
∴∠A=∠CBD,∠C=∠C,
∴△ABC∽△BCD,
∴AC:BC=BC:CD,
∴AC:AD=AD:CD,
∴点D为AC的黄金分割点,
∴AD=AC=×8=4()=4.
故选:B.
6.解:①角是有公共端点的两条射线组成的图形,只有度数相等,两条射线是可以无限延长的,它们是相似形.所以①正确.
②所有菱形的四条边的比相等,但不能判断它们的对应角相等,它们不一定是相似形.所以②不正确.
③所以正方形的四个角都是90°,对应边的比都相等,它们是相似形.所以③正确.
④圆是以定点为圆心,定长为半径所组成的图形,它们只有大小不同,形状都相同,是相似形.所以④正确.
故选:B.
7.解:∵△ABC∽△A′B′C′,
∴AB:A′B′=AC:A′C′
∴12:16=15:A′C′
∴A′C′=20.
故选:B.
8.解:∵DE把△ABC为面积相等的两部分,∴△ADE的面积是△ABC面积的一半,
∵DE∥BC,
∴△ADE∽△ABC,则=,
∵△ADE的面积=AD?AE?sinA,
△ABC的面积=AB?AC?sinA,
∴=,即=,
∴DE:BC=1:.
故选:A.
9.解:把图上距离看作单位1,设A、B和C、D两地的实际距离分别为x和y,则:
1:5000=1:x,
解得x=5000,
1:20000=1:y,
解得y=20000,
∴x:y=5000:20000=1:4.
故选:C.
10.解:根据位似图形的定义可知两个图形不仅是相似图形而且每组对应点所在的直线都经过同一个点,对应边互相平行(或共线),所以位似图形的是第一个、第二个和第三个.
故选:D.
二.填空题
11.解:∵相似三角形的一组对应边长分别为15和27,
∴其相似比为15:27=5:9,
相似三角形的相似比等于对应周长的比,
可设较小的三角形的周长为5x,则另一三角形的周长为9x,
9x﹣5x=36,解得x=9,
所以较小三角形的周长为5x=45,
故答案为45.
12.解:根据题意得:∠AEB=∠CED,
∵∠ABE=∠CDE=90°,
∴△ABE∽△CDE
∴,
解得:AB=12米,
即树高12米.
故答案为12米.
13.解:若两个几何图形F与F′相似,而且对应点连线交于同一点O,则称F与F′关于点O位似,O叫做位似中心.把一个几何图形变换成与之位似的图形,叫做位似变换.因而成位似的三角形是△AOD与△COB、△AOD与△COB.故找出一对是位似图形的三角形:答案不唯一,如△AOB与△COD或△AOD与△COB.
14.解:根据射影定理可得:AB2=BD×BC;AC2=CD×BC,
∴解得:BD=1,AC=.
故答案为:1,.
15.解:∵A(0,1),B(2,﹣3),C(﹣2,0),
∴由勾股定理得:AC==,
AB==2,
BC==5,
∵D(0,2),E(4,﹣6),F(﹣4,0),
∴DE==4,
EF==10,
DF==2,
∴===,
∴△ABC∽△DEF,
∴△ABC与△DEF的面积之比是()2==1:4,
故答案为:1:4.
16.解:∵DC∥EF∥AB,
∴==2,又AG=5cm,
∴GC=2.5cm.
=,CF=2cm,
∴BC=6cm.
故答案为:6,2.5.
17.解:因为第一个黄金三角形的周长=1+1+k=2+k,
第二个黄金三角形的周长=2k+k2=k(2+k),
第三个黄金三角形的周长=2k2+k3=k2(2+k),
所以第2006个黄金三角形的周长是k2005(2+k).
故答案为k2005(2+k).
18.解:∵,
∴x2=12,
∴x=±2.
故答案为:±2.
19.解:设===k≠0,
则x=3k,y=4k,z=6k,
===.
故答案为:.
20.解:在平行四边形ABCD中,AB=12cm,AD=5cm,E为AD的中点.则BC=AD=5cm.DE=2.5cm.CD=AB=12cm.
∵△CBF∽△CDE
∴=.即=,
∴BF=
∴AF=AB﹣BF=12﹣=cm.
故答案是:.
三.解答题
21.(1)解:在Rt△APD中,PA=AB=1,AD=2,
∴PD==,
∴AM=AF=PF﹣PA=PD﹣PA=﹣1,
DM=AD﹣AM=2﹣(﹣1)=3﹣;
(2)证明:∵AM2=(﹣1)2=6﹣2,AD?DM=2(3﹣)=6﹣2,
∴AM2=AD?DM;
(3)点M是AD的黄金分割点.理由如下:
∵AM2=AD?DM,
∴═=,
∴点M是AD的黄金分割点.
22.解:(1)相似,等边三角形各角相等,各边成比例,故两这个三角形相似得到.
(2)相似,易知两三角形均为等腰直角三角形,
符合两组对应边的比相等且相应的夹角相等的两个三角形相似的判定.
23.解:延长PO到E,延长线与圆O交于点E,连接EB,AC.
∵PA=9,AB=7,
∴PB=16.
∵四边形ACEB为圆O的内接四边形,
∴∠ACP=∠E,又∠P=∠P,
∴△ACP∽△EBP,
∴=,即=,
∴=,
解得:OC=5或x=﹣5
(舍去),
则EC=2OC=10,即⊙O直径的长是10.
24.解:∵x:y:z=3:5:7,
∴设x=3k、y=5k、z=7k,
则==.
25.解:
26.解:(1)∵A、B两点的坐标分别为(40,0),(0,30),
∴OA=40,OB=30.
∵动直线EF从x轴开始以每秒1个单位长度的速度向上平行移动(即EF∥x轴),
∴t=15时,BE=30﹣15=15,
∵EF∥x轴,
∴EF是△BOA的中位线,
∴EF=OA=20,
∴S△PEF=EF?OE=×20×15=150;
(2)∵动点P从点A开始在线段AO上以每秒2个长度单位的速度向原点O运动,动直线EF从x轴开始以每秒1个单位长度的速度向上平行移动(即EF∥x轴),
∴OE=t,OP=40﹣2t,
∴当△EOP∽△BOA时,=,即=,解得t=12(秒);
当△EOP∽△AOB时,=,即=.解得t=(秒).
综上所述,当t=12秒或t=秒时,△EOP与△BOA相似.
27.解:(1)两条直线被平行线所截,对应线段成比例.即:AC:CE=BD:DF.
(2)为了把MN分成2:3两部分,从M点出发作一条射线MT,与MN有适当的夹角.
MT上取AB两点.使MA=2单位,MB=5单位,(即MA:AB=2:3).
连接NB.过A作NB的平行线,与MN相交于P.则MP:PN=2:3.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
