7.4 由三角函数值求锐角 课件(共22张PPT)
文档属性
| 名称 | 7.4 由三角函数值求锐角 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-20 00:00:00 | ||
图片预览






文档简介
7.4 由三角函数值求锐角
第7章 锐角三角函数
2020-2021学年度苏科版九年级下册
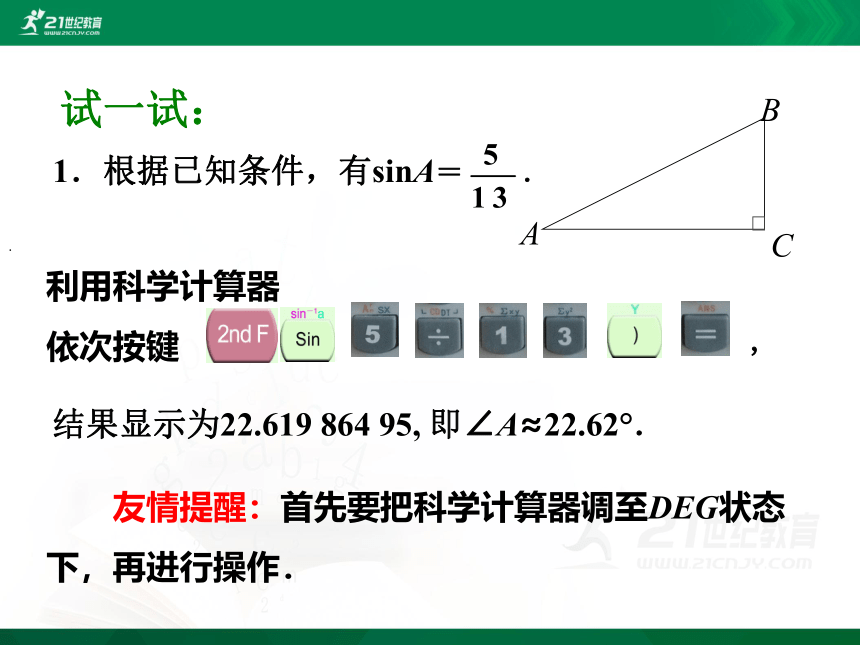
试一试:
1.根据已知条件,有sinA= .
.
利用科学计算器
依次按键
A
C
B
结果显示为22.619 864 95, 即∠A≈22.62°.
,
友情提醒:首先要把科学计算器调至DEG状态下,再进行操作.
你知道为什么要先按 功能键吗?
想一想:
例1 求满足下列条件的锐角A(精确到0.01°):
(2)tanA=2 .
(1)cosA= ;
解:(1)依次按键
,
显示结果为75.522 487 81,即∠A≈75.52°.
(2)依次按键
,
显示结果为63.434 948 82,即∠A≈63.43°.
练一练:
1. 求满足下列条件的锐角A(精确到0.01°):
(2)cosA= 0.23 ;
(3)tanA= 10 .
(1)sinA= ;
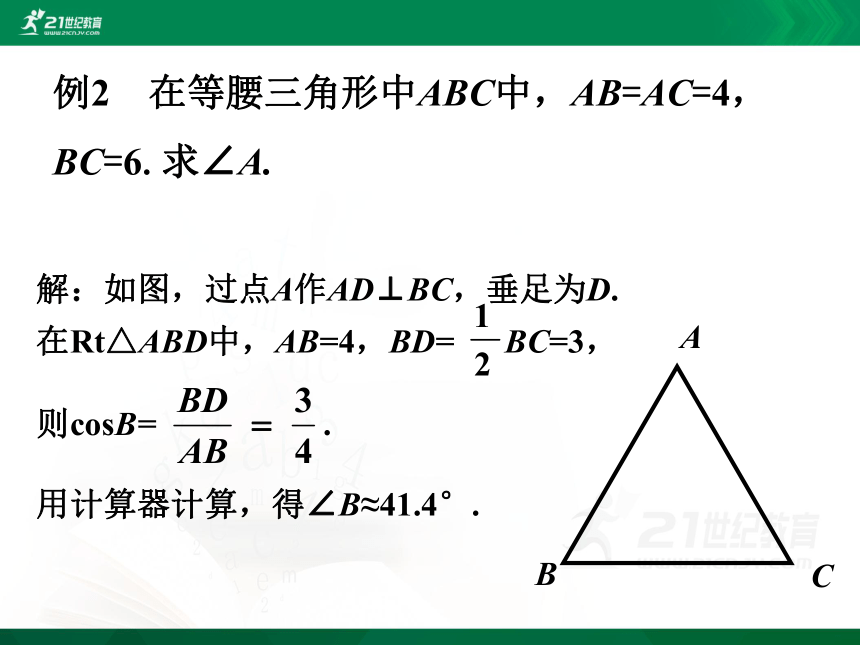
例2 在等腰三角形中ABC中,AB=AC=4,BC=6.求∠A.
A
B
C
解:如图,过点A作AD⊥BC,垂足为D.
在Rt△ABD中,AB=4,BD= BC=3,
则cosB= .
用计算器计算,得∠B≈41.4°.
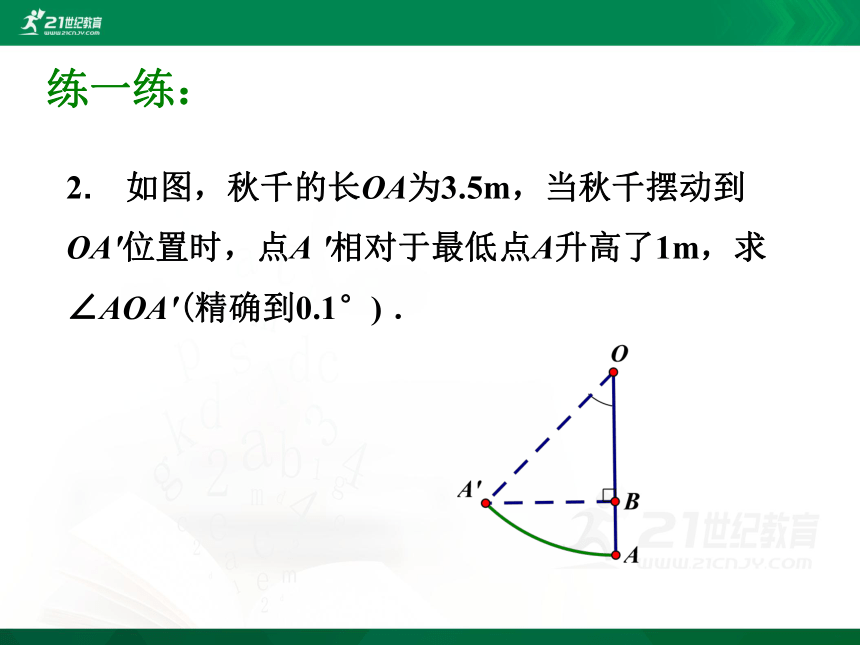
2. 如图,秋千的长OA为3.5m,当秋千摆动到OA′位置时,点A ′相对于最低点A升高了1m,求∠AOA′(精确到0.1°) .
练一练:
思考:
已知∠A为锐角,且cosA = ,∠A的取值范围是( )
A. 0°<∠A<30° B. 30°<∠A<45°
C. 45°<∠A<60° D. 60°<∠A<90°
如果不用计算器,你能根据三角函数的增减性判断出来吗?
D
求下列各式的值:
(1)1-2 sin30°cos30°
(2)3tan30°-tan45°+2sin60°
(3)
练习
2. 在Rt△ABC中,∠C=90°,
求∠A、∠B的度数.
B
A
C
3. 已知sinθ=0.82904,求∠θ的大小.
4. 一梯子斜靠在一面墙上,已知梯子长4m,梯子位于地面上的一端离墙壁2.5m,求梯子与地面所成的锐角.
A
B
C
“斜而未倒”
BC=5.2m
AB=54.5m
α
你能求出塔偏离垂直中心线有多少度吗?
例1 求满足下列条件的锐角A(精确到0.01°):
(2)tanA=2 .
(1)cosA= ;
解:(1)依次按键
,
显示结果为75.522 487 81,即∠A≈75.52°.
(2)依次按键
,
显示结果为63.434 948 82,即∠A≈63.43°.
典例分析
例2 在等腰三角形中ABC中,AB=AC=4,BC=6.
求∠A.
A
B
C
典例分析
解:如图,过点A作AD⊥BC,垂足为D.
在Rt△ABD中,AB=4,BD= BC=3,
则cosB= .
用计算器计算,得∠B≈41.4°.
如图,一段公路弯道AB两端的距离为200m,
AB的半径为1000m,求弯道的长(精确到0.1m).
⌒
⌒
C
A
B
O
课内练习:
在Rt△ABC中,∠C=90°,根据下列
条件求各个锐角(精确到 ):
C
A
B
(1)AB=3,AC=1;
(2)AC=4,BC=5.
课内练习:
2.如图,测得一商场自动扶梯的长L为8米,该自动扶梯到达的高度h是5米.问自动扶梯与地面所成的角θ是多少度(精确到 )?
L
h
θ
课内练习:
练一练
1.sin70°=
cos50°=
(3)tanA= ,则A=
(4)2sinA- =0, 则A=
2.(1)sinA=0.3475 ,则A= (精确到1")
(2)cosA=0.4273,则A= (精确到1")
0.9397
0.6428
2°20'4"
64°42'13"
30°
60°
3.已知sinα·cos30°= ,求锐角α.
4. 一梯子斜靠在一面墙上,已知梯子长4m,梯子位于地面上的一端离墙壁2.5m,求梯子与地面所成的锐角.
5 . 一个人由山底爬到山顶,需先爬400的山坡300m,再爬300 的山坡100m,求山高(结果精确到0.01m).
练一练
由锐角的三角函数值反求锐角
小结 拓展
填表:已知一个角的三角函数值,求这个角的度数(逆向思维).
∠A=30°
∠A=30°
∠A=30°
∠A=45°
∠A=45°
∠A=45°
∠A=60°
∠A=60°
∠A=60°
谢谢聆听
第7章 锐角三角函数
2020-2021学年度苏科版九年级下册
试一试:
1.根据已知条件,有sinA= .
.
利用科学计算器
依次按键
A
C
B
结果显示为22.619 864 95, 即∠A≈22.62°.
,
友情提醒:首先要把科学计算器调至DEG状态下,再进行操作.
你知道为什么要先按 功能键吗?
想一想:
例1 求满足下列条件的锐角A(精确到0.01°):
(2)tanA=2 .
(1)cosA= ;
解:(1)依次按键
,
显示结果为75.522 487 81,即∠A≈75.52°.
(2)依次按键
,
显示结果为63.434 948 82,即∠A≈63.43°.
练一练:
1. 求满足下列条件的锐角A(精确到0.01°):
(2)cosA= 0.23 ;
(3)tanA= 10 .
(1)sinA= ;
例2 在等腰三角形中ABC中,AB=AC=4,BC=6.求∠A.
A
B
C
解:如图,过点A作AD⊥BC,垂足为D.
在Rt△ABD中,AB=4,BD= BC=3,
则cosB= .
用计算器计算,得∠B≈41.4°.
2. 如图,秋千的长OA为3.5m,当秋千摆动到OA′位置时,点A ′相对于最低点A升高了1m,求∠AOA′(精确到0.1°) .
练一练:
思考:
已知∠A为锐角,且cosA = ,∠A的取值范围是( )
A. 0°<∠A<30° B. 30°<∠A<45°
C. 45°<∠A<60° D. 60°<∠A<90°
如果不用计算器,你能根据三角函数的增减性判断出来吗?
D
求下列各式的值:
(1)1-2 sin30°cos30°
(2)3tan30°-tan45°+2sin60°
(3)
练习
2. 在Rt△ABC中,∠C=90°,
求∠A、∠B的度数.
B
A
C
3. 已知sinθ=0.82904,求∠θ的大小.
4. 一梯子斜靠在一面墙上,已知梯子长4m,梯子位于地面上的一端离墙壁2.5m,求梯子与地面所成的锐角.
A
B
C
“斜而未倒”
BC=5.2m
AB=54.5m
α
你能求出塔偏离垂直中心线有多少度吗?
例1 求满足下列条件的锐角A(精确到0.01°):
(2)tanA=2 .
(1)cosA= ;
解:(1)依次按键
,
显示结果为75.522 487 81,即∠A≈75.52°.
(2)依次按键
,
显示结果为63.434 948 82,即∠A≈63.43°.
典例分析
例2 在等腰三角形中ABC中,AB=AC=4,BC=6.
求∠A.
A
B
C
典例分析
解:如图,过点A作AD⊥BC,垂足为D.
在Rt△ABD中,AB=4,BD= BC=3,
则cosB= .
用计算器计算,得∠B≈41.4°.
如图,一段公路弯道AB两端的距离为200m,
AB的半径为1000m,求弯道的长(精确到0.1m).
⌒
⌒
C
A
B
O
课内练习:
在Rt△ABC中,∠C=90°,根据下列
条件求各个锐角(精确到 ):
C
A
B
(1)AB=3,AC=1;
(2)AC=4,BC=5.
课内练习:
2.如图,测得一商场自动扶梯的长L为8米,该自动扶梯到达的高度h是5米.问自动扶梯与地面所成的角θ是多少度(精确到 )?
L
h
θ
课内练习:
练一练
1.sin70°=
cos50°=
(3)tanA= ,则A=
(4)2sinA- =0, 则A=
2.(1)sinA=0.3475 ,则A= (精确到1")
(2)cosA=0.4273,则A= (精确到1")
0.9397
0.6428
2°20'4"
64°42'13"
30°
60°
3.已知sinα·cos30°= ,求锐角α.
4. 一梯子斜靠在一面墙上,已知梯子长4m,梯子位于地面上的一端离墙壁2.5m,求梯子与地面所成的锐角.
5 . 一个人由山底爬到山顶,需先爬400的山坡300m,再爬300 的山坡100m,求山高(结果精确到0.01m).
练一练
由锐角的三角函数值反求锐角
小结 拓展
填表:已知一个角的三角函数值,求这个角的度数(逆向思维).
∠A=30°
∠A=30°
∠A=30°
∠A=45°
∠A=45°
∠A=45°
∠A=60°
∠A=60°
∠A=60°
谢谢聆听
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
