7.5 解直角三角形 课件(共32张PPT)
文档属性
| 名称 | 7.5 解直角三角形 课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-20 07:40:54 | ||
图片预览








文档简介
7.5 解直角三角形
第7章 锐角三角函数
2020-2021学年度苏科版九年级下册
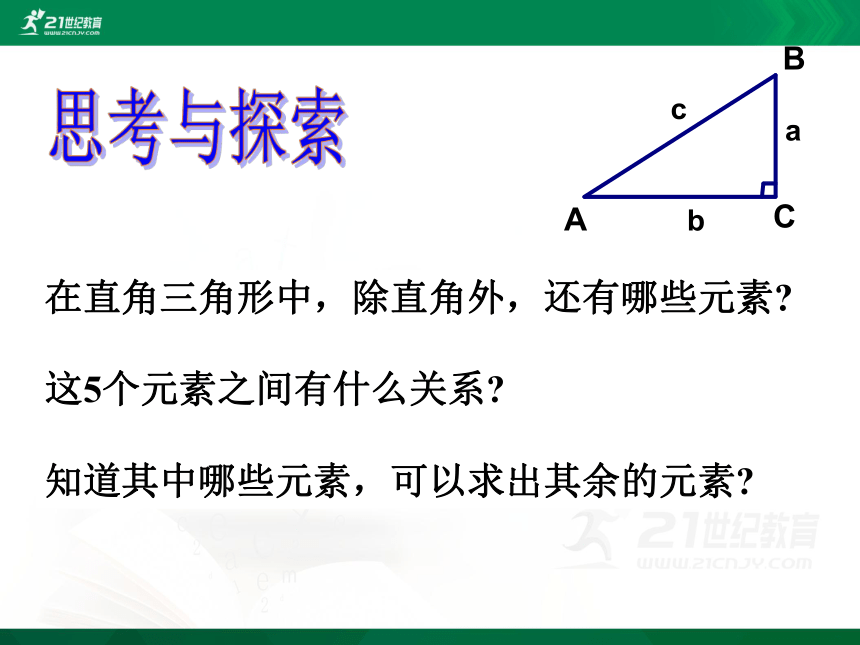
在直角三角形中,除直角外,还有哪些元素?
这5个元素之间有什么关系?
知道其中哪些元素,可以求出其余的元素?
思考与探索
如图,在Rt△ABC中,∠C为直角,
其余5个元素之间有以下关系:
(2)锐角之间的关系:
∠A+ ∠B=90°(直角三角形的两个锐角互余)
(1)三边之间关系:
(3)边角之间的关系:
(勾股定理)
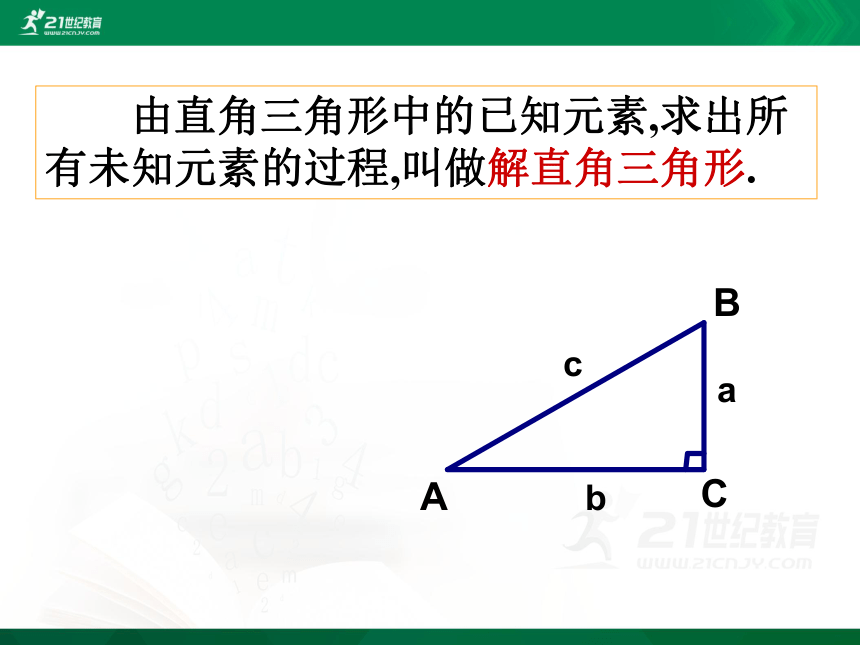
由直角三角形中的已知元素,求出所有未知元素的过程,叫做解直角三角形.
例题分析
1、在Rt△ABC中,∠C=90°,∠A=30°,a=5.解这个直角三角形 .
解:在Rt△ABC中,∠C=90°,∠A=30°,
∴∠B=90°-∠A=90°-30°=60°.
∵sinA= ,
∴c=
∵ ,
∴ b=a·tanB=5 ·tan60°= .
例题分析
2、已知:在Rt△ABC中,∠C=90°,a=104,
b= 20.49.求:
(1) c的值(精确到0.01);
(2)求∠A、∠B的大小(精确到0.01).
提示:通过计算器求值.
基础练习
在Rt△ABC中,∠C=90°,a、b、c分别为
∠A 、∠B、 ∠C的对边.根据已知条件,
解直角三角形.
(1) a=9, b=6;
(2) ∠A = 18 °, c=13.
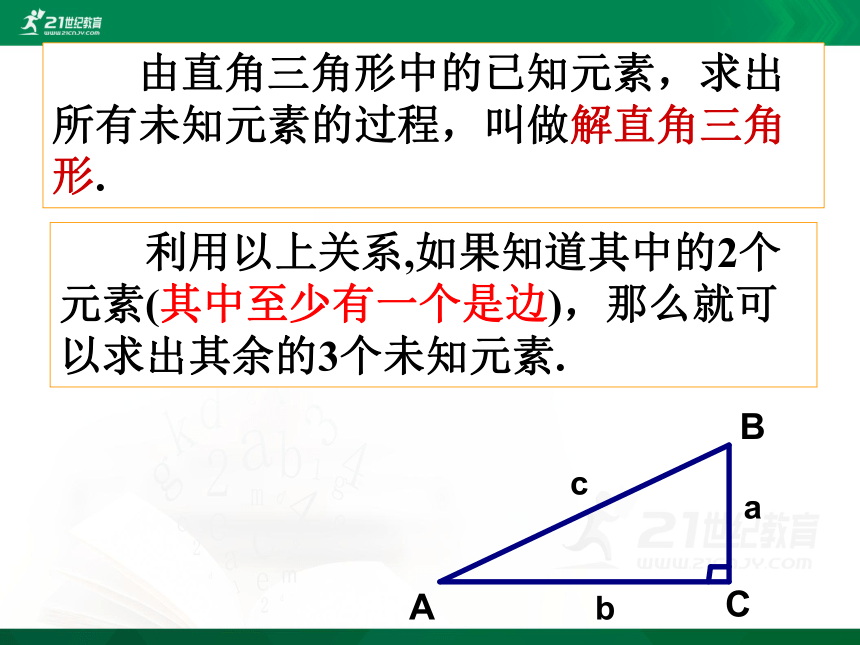
利用以上关系,如果知道其中的2个元素(其中至少有一个是边),那么就可以求出其余的3个未知元素.
由直角三角形中的已知元素,求出所有未知元素的过程,叫做解直角三角形.
例题分析
3、在三角形ABC中,AC=8, ∠B= 45 °, ∠A = 30°.求AB.
解:过点C作CD⊥AB,垂足为D.
在Rt△ADC中,
AD=AC·cos30°=8× =4 ,
CD=AC·sin30°=8× =4.
在Rt△BCD中,∵∠B=45°,
∴BD=CD=4.
∴AB=AD+DB=4
例题分析
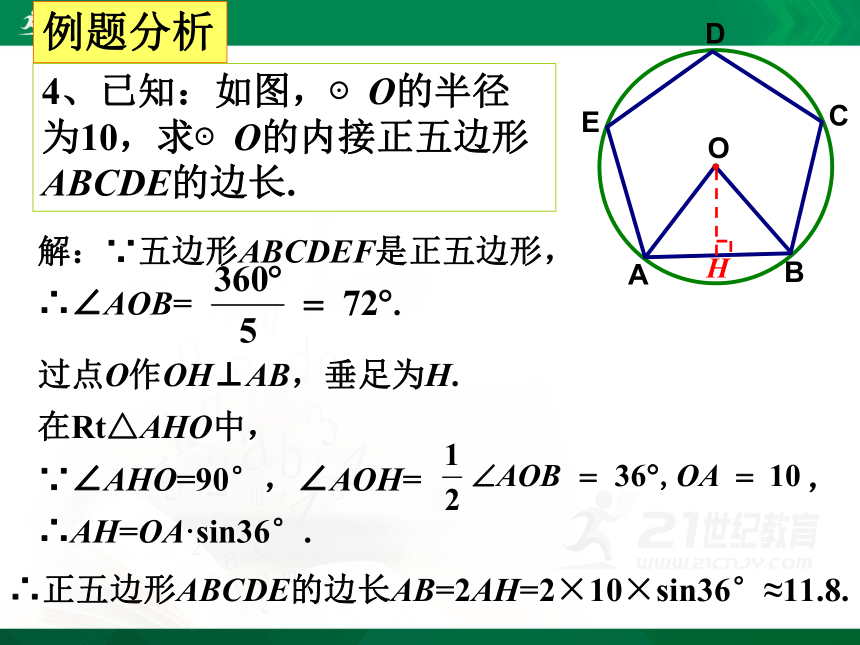
4、已知:如图,⊙O的半径为10,求⊙O的内接正五边形ABCDE的边长.
H
解:∵五边形ABCDEF是正五边形,
∴∠AOB=
过点O作OH⊥AB,垂足为H.
在Rt△AHO中,
∵∠AHO=90°,∠AOH= ,
∴AH=OA·sin36°.
∴正五边形ABCDE的边长AB=2AH=2×10×sin36°≈11.8.
在Rt△ABC中,CD是斜边上的高.
若AC=8,cosA=0.8,求△ABC的面积.
随堂练习
如图,在△ABC中,∠ACB=90°,
BC=15cm,∠BAC=30°,∠DAC=45°,
求AD.
A
C
B
D
能力提升
在Rt△ABC中,∠C=90°,∠A,∠B,∠C
的对边分别是a,b,c.且a+b=4 , , 解这个直角三角形.
能力提升
A
B
C
在山脚C处测得山顶A的仰角为450.沿着坡角为30 °的斜坡前进300米到达D点,在D点测得山顶A的仰角为600 ,求山高AB.
30°
D
E
F
x
变式训练
五星红旗你是我的骄傲,五星红旗我为你自豪……
如何测量旗杆的高度?
【想一想】
如图,有两棵树,一棵高8m,另一棵高2m,两树相距8m,一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞多远?
A
B
C
8m
8m
2m
【做一做】
如图,为测量旗杆的高度,在C点测得A点的仰角为30°,点C到点B的距离56.3,求旗杆的高度
(精确到0.1m).
A
C
B
如图,在Rt△ABC中, ∠C为直角,其余5个元素之间有以下关系:
(1)三边之间关系:
(勾股定理).
(2)锐角之间的关系:
∠A+∠B=90°(直角三角形的两个锐角互余).
(3)边角之间的关系:
【议一议】
A
c
b
a
C
B
由直角三角形的边、角中的已知元素,求出所有边、角中的未知元素的过程,叫做解直角三角形.
【定义】
例1、在Rt△ABC中,∠C=90°,∠A=30°,a=5.解这个直角三角形 .
解:在Rt△ABC中,∠C=90°,∠A=30°,
∴∠B=90°-∠A=90°-30°=60°.
∵sinA= ,
∴c=
∵ ,
∴ b=a·tanB=5 ·tan60°= .
【练一练】
例2 已知:在Rt△ABC中,∠C=90°,a=104,
b=20.49.
(1)求c的值(精确到0.01);
(2)求∠A、∠B的大小(精确到0.01°).
提示:通过计算器求值.
1.在Rt△ABC中,∠C=90°,根据下列条件解直角三
角形(边长精确到0.1,角度精确到0.1°):
(1)a=9 , b=6; (2) ∠A = 18°,∠C = 13.
2.如图,某地修建高速公路,要从B地向C地修一座隧道(B、C在同一水平面上).为了测量B、C两地之间的距离,某工程师乘坐热气球从C地出发,垂直上升100m到达A处,在A处观察B地的俯角为30°,求:B、C两地之间的距离.
【考一考】
【例3】 如图,在△ABC中,AC=8,∠B=45°,∠A=30°,求AB.
解直角三角形问题的前提条件是在直角三角形中,因为本题△ABC不是直角三角形,因此要设法构造直角三角形.
【练一练】
解:过点C作CD⊥AB,垂足为D.
在Rt△ADC中,
AD=AC·cos30°=8× =4 ,
CD=AC·sin30°=8× =4.
在Rt△BCD中,∵∠B=45°,
∴BD=CD=4.
∴AB=AD+DB=4
【例4】 如图,⊙O的半径为10,求⊙O的内接正五边形ABCDE的边长(精确到0.1).
通过作等腰三角形的高,将等腰三角形转化为直角三角形,借助解直角三角形来解决问题.
【练一练】
H
解:∵五边形ABCDEF是正五边形,
∴∠AOB=
过点O作OH⊥AB,垂足为H.
在Rt△AHO中,
∵∠AHO=90°,∠AOH= ,
∴AH=OA·sin36°.
∴正五边形ABCDE的边长AB=2AH=2×10×sin36°≈11.8.
1.在平行四边形ABCD中,∠A=60°,AB=8,AD=6,求平行四边形的面积.
2.求半径为12的圆的内接正八边形的边长(精确到0.1).
【考一考】
3、在地面上选取一个点C,在A、C两点间选取一点D,测得CD=14米,在C、D两点处分别用测角器测得铁塔顶端B的仰角为α=30°和β=45°测角仪支架的高度为1.2米.(精确到0.1米,tan300=0.55)
你算出铁塔的高度吗?
解直角三角
形的概念
(勾股定理)
三边之间关系
边角之间关系(锐角三角函数)
简单应用
两锐角之间关系
【小结】
1、通过做适当的辅助线,构造直角三角形.
2、有公共直角边的两个直角三角形,一般设出公共边的长度(x米)在另一个直角三角形中根据锐角三角函数关系列出程.
3、测量底部不能到达的物体的高度,通常选用这种方法.
归纳总结
谢谢聆听
第7章 锐角三角函数
2020-2021学年度苏科版九年级下册
在直角三角形中,除直角外,还有哪些元素?
这5个元素之间有什么关系?
知道其中哪些元素,可以求出其余的元素?
思考与探索
如图,在Rt△ABC中,∠C为直角,
其余5个元素之间有以下关系:
(2)锐角之间的关系:
∠A+ ∠B=90°(直角三角形的两个锐角互余)
(1)三边之间关系:
(3)边角之间的关系:
(勾股定理)
由直角三角形中的已知元素,求出所有未知元素的过程,叫做解直角三角形.
例题分析
1、在Rt△ABC中,∠C=90°,∠A=30°,a=5.解这个直角三角形 .
解:在Rt△ABC中,∠C=90°,∠A=30°,
∴∠B=90°-∠A=90°-30°=60°.
∵sinA= ,
∴c=
∵ ,
∴ b=a·tanB=5 ·tan60°= .
例题分析
2、已知:在Rt△ABC中,∠C=90°,a=104,
b= 20.49.求:
(1) c的值(精确到0.01);
(2)求∠A、∠B的大小(精确到0.01).
提示:通过计算器求值.
基础练习
在Rt△ABC中,∠C=90°,a、b、c分别为
∠A 、∠B、 ∠C的对边.根据已知条件,
解直角三角形.
(1) a=9, b=6;
(2) ∠A = 18 °, c=13.
利用以上关系,如果知道其中的2个元素(其中至少有一个是边),那么就可以求出其余的3个未知元素.
由直角三角形中的已知元素,求出所有未知元素的过程,叫做解直角三角形.
例题分析
3、在三角形ABC中,AC=8, ∠B= 45 °, ∠A = 30°.求AB.
解:过点C作CD⊥AB,垂足为D.
在Rt△ADC中,
AD=AC·cos30°=8× =4 ,
CD=AC·sin30°=8× =4.
在Rt△BCD中,∵∠B=45°,
∴BD=CD=4.
∴AB=AD+DB=4
例题分析
4、已知:如图,⊙O的半径为10,求⊙O的内接正五边形ABCDE的边长.
H
解:∵五边形ABCDEF是正五边形,
∴∠AOB=
过点O作OH⊥AB,垂足为H.
在Rt△AHO中,
∵∠AHO=90°,∠AOH= ,
∴AH=OA·sin36°.
∴正五边形ABCDE的边长AB=2AH=2×10×sin36°≈11.8.
在Rt△ABC中,CD是斜边上的高.
若AC=8,cosA=0.8,求△ABC的面积.
随堂练习
如图,在△ABC中,∠ACB=90°,
BC=15cm,∠BAC=30°,∠DAC=45°,
求AD.
A
C
B
D
能力提升
在Rt△ABC中,∠C=90°,∠A,∠B,∠C
的对边分别是a,b,c.且a+b=4 , , 解这个直角三角形.
能力提升
A
B
C
在山脚C处测得山顶A的仰角为450.沿着坡角为30 °的斜坡前进300米到达D点,在D点测得山顶A的仰角为600 ,求山高AB.
30°
D
E
F
x
变式训练
五星红旗你是我的骄傲,五星红旗我为你自豪……
如何测量旗杆的高度?
【想一想】
如图,有两棵树,一棵高8m,另一棵高2m,两树相距8m,一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞多远?
A
B
C
8m
8m
2m
【做一做】
如图,为测量旗杆的高度,在C点测得A点的仰角为30°,点C到点B的距离56.3,求旗杆的高度
(精确到0.1m).
A
C
B
如图,在Rt△ABC中, ∠C为直角,其余5个元素之间有以下关系:
(1)三边之间关系:
(勾股定理).
(2)锐角之间的关系:
∠A+∠B=90°(直角三角形的两个锐角互余).
(3)边角之间的关系:
【议一议】
A
c
b
a
C
B
由直角三角形的边、角中的已知元素,求出所有边、角中的未知元素的过程,叫做解直角三角形.
【定义】
例1、在Rt△ABC中,∠C=90°,∠A=30°,a=5.解这个直角三角形 .
解:在Rt△ABC中,∠C=90°,∠A=30°,
∴∠B=90°-∠A=90°-30°=60°.
∵sinA= ,
∴c=
∵ ,
∴ b=a·tanB=5 ·tan60°= .
【练一练】
例2 已知:在Rt△ABC中,∠C=90°,a=104,
b=20.49.
(1)求c的值(精确到0.01);
(2)求∠A、∠B的大小(精确到0.01°).
提示:通过计算器求值.
1.在Rt△ABC中,∠C=90°,根据下列条件解直角三
角形(边长精确到0.1,角度精确到0.1°):
(1)a=9 , b=6; (2) ∠A = 18°,∠C = 13.
2.如图,某地修建高速公路,要从B地向C地修一座隧道(B、C在同一水平面上).为了测量B、C两地之间的距离,某工程师乘坐热气球从C地出发,垂直上升100m到达A处,在A处观察B地的俯角为30°,求:B、C两地之间的距离.
【考一考】
【例3】 如图,在△ABC中,AC=8,∠B=45°,∠A=30°,求AB.
解直角三角形问题的前提条件是在直角三角形中,因为本题△ABC不是直角三角形,因此要设法构造直角三角形.
【练一练】
解:过点C作CD⊥AB,垂足为D.
在Rt△ADC中,
AD=AC·cos30°=8× =4 ,
CD=AC·sin30°=8× =4.
在Rt△BCD中,∵∠B=45°,
∴BD=CD=4.
∴AB=AD+DB=4
【例4】 如图,⊙O的半径为10,求⊙O的内接正五边形ABCDE的边长(精确到0.1).
通过作等腰三角形的高,将等腰三角形转化为直角三角形,借助解直角三角形来解决问题.
【练一练】
H
解:∵五边形ABCDEF是正五边形,
∴∠AOB=
过点O作OH⊥AB,垂足为H.
在Rt△AHO中,
∵∠AHO=90°,∠AOH= ,
∴AH=OA·sin36°.
∴正五边形ABCDE的边长AB=2AH=2×10×sin36°≈11.8.
1.在平行四边形ABCD中,∠A=60°,AB=8,AD=6,求平行四边形的面积.
2.求半径为12的圆的内接正八边形的边长(精确到0.1).
【考一考】
3、在地面上选取一个点C,在A、C两点间选取一点D,测得CD=14米,在C、D两点处分别用测角器测得铁塔顶端B的仰角为α=30°和β=45°测角仪支架的高度为1.2米.(精确到0.1米,tan300=0.55)
你算出铁塔的高度吗?
解直角三角
形的概念
(勾股定理)
三边之间关系
边角之间关系(锐角三角函数)
简单应用
两锐角之间关系
【小结】
1、通过做适当的辅助线,构造直角三角形.
2、有公共直角边的两个直角三角形,一般设出公共边的长度(x米)在另一个直角三角形中根据锐角三角函数关系列出程.
3、测量底部不能到达的物体的高度,通常选用这种方法.
归纳总结
谢谢聆听
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
