7.6 用三角函数解决问题 课件(共29张PPT)
文档属性
| 名称 | 7.6 用三角函数解决问题 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-20 00:00:00 | ||
图片预览






文档简介
7.6 用三角函数解决问题
第7章 锐角三角函数
2020-2021学年度苏科版九年级下册
A
B
C
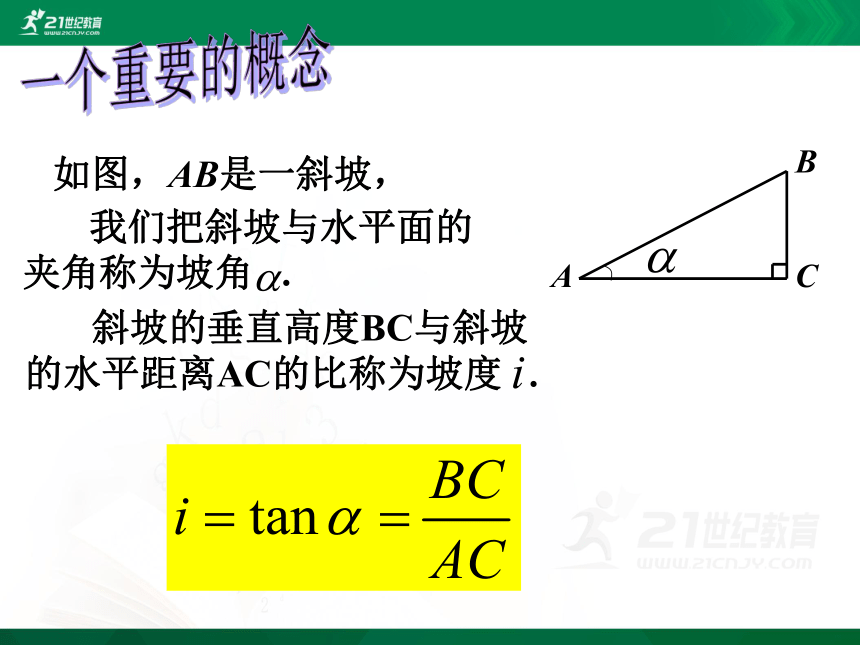
如图,AB是一斜坡,
我们把斜坡与水平面的
夹角称为坡角 .
斜坡的垂直高度BC与斜坡
的水平距离AC的比称为坡度 .
一个重要的概念
1、小明沿着坡角为20°的斜坡向上行走,水平前进了80m,则他上升的高度是多少?
热身训练
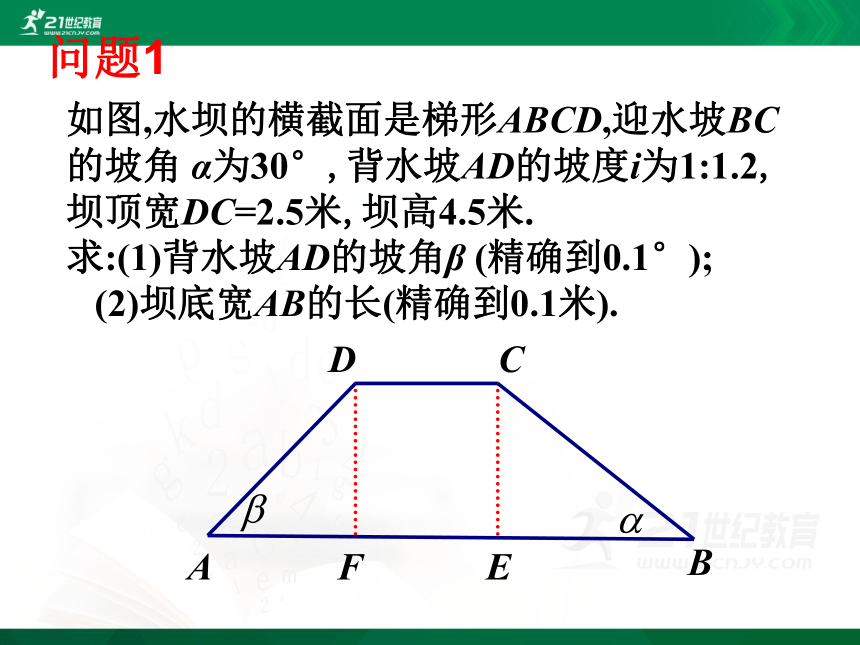
如图,水坝的横截面是梯形ABCD,迎水坡BC
的坡角 α为30°,背水坡AD的坡度i为1:1.2,
坝顶宽DC=2.5米,坝高4.5米.
求:(1)背水坡AD的坡角β (精确到0.1°);
(2)坝底宽AB的长(精确到0.1米).
E
F
问题1
D
C
B
A
(2)在Rt△BEC中,
∠α=30°,∠BCE=90°-30°=60°,
EB=CE·tan∠BCE=4.5×tan60°.
在Rt△AFD中,
∵ =1∶1.2,
∴AF=1.2DF=1.2×4.5=5.4.
又FE=DC=2.5,
∴AB=AF+FE+EB=5.4+2.5+4.5×tan60°≈15.7.
解:作CE⊥AB,垂足分别为E、F.
(1)背水坡AD的坡度i=tanβ=1∶1.2= .
用计算器计算,得β≈39.8°.
E
F
D
C
B
A
G
H
K
在上题中,为了提高堤坝的 防洪能力,市防汛指挥部决定加固堤坝,要求坝顶CD加宽0.5米,背水坡AD的坡度改为1:1.4,已知堤坝的总长度为5㎞,求完成该项工程所需的土方(精确到0.1米3).
思考
如图是沿水库拦河坝的背水坡,将坡顶加宽2米,坡度由原来的1:2改为1:2.5,已知坝高6米,坝长50米.
求(1)加宽部分横断面AFEB的面积;
(2)完成这一工程需要多少土方?
练习1
E
F
D
C
B
A
G
H
A
B
C
D
如图,斜坡AC的坡度(坡比)为1:
AC=10米.坡顶有一旗杆BC,旗杆顶端B点
与A点有一条彩带AB相连,AB=14米.
试求旗杆BC的高度.
E
练习2
A
B
O
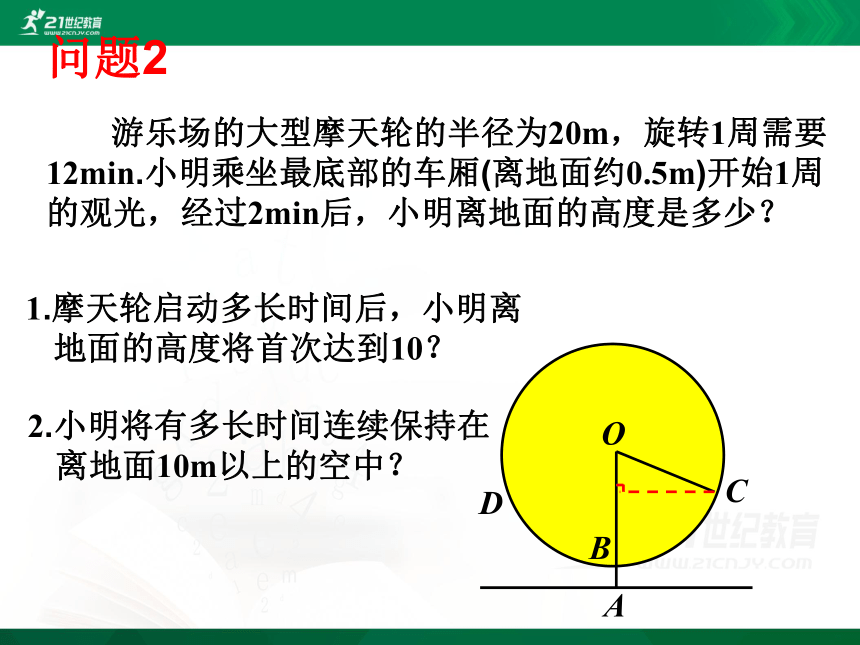
游乐场的大型摩天轮的半径为20m,旋转1周需要12min.小明乘坐最底部的车厢(离地面约0.5m)开始1周的观光,经过2min后,小明离地面的高度是多少?
C
D
1.摩天轮启动多长时间后,小明离
地面的高度将首次达到10?
2.小明将有多长时间连续保持在
离地面10m以上的空中?
问题2
解:如图,用⊙O表示摩天轮,A、B分别表示小明的出发点和2min后的到达点.由题意知,OB=20,∠BOA=360°÷6=60°.
作BC⊥OA,垂足为C.
在Rt△OCB中,
OC=OB·cos∠BOC=20×cos60°=20× =10,
AC=AO-CO=20-10=10.
因为摩天轮底部与地面相距0.3m,所以小明离地面的高度应为10.3m.
答:2min后小明离地面10.3m.
已知跷跷板长4m,当跷跷板的一端碰到地面
时,另一端离地面1.5m.求此时跷跷板与地面的夹角(精确到0.1°).
A
B
O
C
练习3
为了测量停留在空中的气球高度,小明在某处利用测角仪测得气球的仰角(从低处观测高处的目标时,视线与水平线所成的锐角)为27°,然后他沿气球方向前进了50m,再次测得仰角为40°.如果测角仪高度忽略不计, 那么气球的高度是多少(精确到0.1m)?
A
D
B
C
问题3
∵ AD-BD=50,
∴
∴
答:气球的高度约为64.9m.
解:如图,点A、B、C分别表示小明两次观测处及气球位置.由题意知,∠CAD=40°,CD⊥AD,AB=50m,设CD=xm.
在Rt△BCD中,
由tan40°= ,得BD=
在Rt△ADC中,由tan27°= ,得
如图,在一笔直的海岸线上有A,B两个观测站,A在B的正西方向,AB=2km,从A测得船C在北偏东60°的方向,从B测得船C在北偏西45°的方向.求船C离海岸线的距离.
A
B
C
2km
60°
45°
D
练习4
概念回顾
1.我们学过哪些三角函数?
2.还记得哪些特殊角的三角函数值?
3.勾股定理有哪些重要知识点?
【例题讲解】
1.如图,水坝的横截面是梯形ABCD,迎水坡BC的坡角为30°,背水坡AD的坡度为1:1.2,坝顶宽DC=2.5m,坝高4.5m.
求:(1)背水坡AD的坡角(精确到0.1°);
(2)坝底宽AB的长(精确到0.1m).
(2)在Rt△BEC中,
∠α=30°,∠BCE=90°-30°=60°,
EB=CE·tan∠BCE=4.5×tan60°.
在Rt△AFD中,
∵ =1∶1.2,
∴AF=1.2DF=1.2×4.5=5.4.
又FE=DC=2.5,
∴AB=AF+FE+EB=5.4+2.5+4.5×tan60°≈15.7.
解:作CE⊥AB,垂足分别为E、F.
(1)背水坡AD的坡度i=tanβ=1∶1.2= .
用计算器计算,得β≈39.8°.
思考:在上题中,为了提高堤坝的防洪能力,市防汛指挥部决定加固堤坝,要求坝顶CD加宽0.5m,背水坡AD的坡度改为1:1.4,已知堤坝的总长度为5km,求完成该项工程所需的土方(精确到0.1m3).
2.游乐场的大型摩天轮的半径为20m,旋转1周需要12min.小明从摩天轮的底部(与地面相距0.3m)出开始观光,2min后小明离地面多高?
【例题讲解】
解:如图,用⊙O表示摩天轮,A、B分别表示小明的出发点和2min后的到达点.由题意知,OB=20,∠BOA=360°÷6=60°.
作BC⊥OA,垂足为C.
在Rt△OCB中,
OC=OB·cos∠BOC=20×cos60°=20× =10,
AC=AO-CO=20-10=10.
因为摩天轮底部与地面相距0.3m,所以小明离地面的高度应为10.3m.
答:2min后小明离地面10.3m.
【拓展与延伸】
活动1 根据问题情境,完成下面的问题:
(1) 摩天轮转动多长时间后,小明离地面的高度将首次达到15.3m?
(2) 摩天轮转动一周,小明在离地面30.3m以上的空中有多长时间?
A
D
B
C
3.为了测量停留在空中的气球高度,小明在某处利用测角仪测得气球的仰角(从低处观测高处的目标时,视线与水平线所成的锐角)为27°,然后他沿气球方向前进了50m,再次测得仰角为40°.如果测角仪高度忽略不计, 那么气球的高度是多少(精确到0.1m)?
【例题讲解】
∵ AD-BD=50,
∴
∴
答:气球的高度约为64.9m.
解:如图,点A、B、C分别表示小明两次观测处及气球位置.由题意知,∠CAD=40°,CD⊥AD,AB=50m,设CD=xm.
在Rt△BCD中,
由tan40°= ,得BD=
在Rt△ADC中,由tan27°= ,得
1.在△ABC中,∠C=90°,∠A=45°,则BC∶AC∶AB = .
在△ABC中,∠C=90°,∠A=30°,则BC∶AC∶AB= .
2.在△ABC中,∠C=90°.
(1)已知∠A=30°,BC=8cm,求AB与AC的长;
(2)已知∠A=60°,AC=8cm,求AB与BC的长.
【练习】
3.如图所示,山坡上有一棵与水平面垂直的大树,一场台风过后,大树被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面.已知山坡的坡角 ∠BAC=38?,量得树干倾角∠AEF=23?,大树被折断部分和坡面所成的角∠ADC=60?,AD=4m.
(1)求∠CAE的度数;
(2)求这棵大树折断前的高度?(结果精确到个位,参考数据 , , ).
【练习】
4.单摆的摆长AB为90cm,当它摆动到AB′的位置时, ∠BAB′ =11°,问这时摆球B′A较最低点B升高了多少(精确到1cm)?
【练习】
5.如图,秋千链子的长度为3m,当秋千向两边摆动时,两边的摆动角度均为30?.求它摆动至最高位置与最低位置的高度之差(结果保留根号).
【练习】
谢谢聆听
第7章 锐角三角函数
2020-2021学年度苏科版九年级下册
A
B
C
如图,AB是一斜坡,
我们把斜坡与水平面的
夹角称为坡角 .
斜坡的垂直高度BC与斜坡
的水平距离AC的比称为坡度 .
一个重要的概念
1、小明沿着坡角为20°的斜坡向上行走,水平前进了80m,则他上升的高度是多少?
热身训练
如图,水坝的横截面是梯形ABCD,迎水坡BC
的坡角 α为30°,背水坡AD的坡度i为1:1.2,
坝顶宽DC=2.5米,坝高4.5米.
求:(1)背水坡AD的坡角β (精确到0.1°);
(2)坝底宽AB的长(精确到0.1米).
E
F
问题1
D
C
B
A
(2)在Rt△BEC中,
∠α=30°,∠BCE=90°-30°=60°,
EB=CE·tan∠BCE=4.5×tan60°.
在Rt△AFD中,
∵ =1∶1.2,
∴AF=1.2DF=1.2×4.5=5.4.
又FE=DC=2.5,
∴AB=AF+FE+EB=5.4+2.5+4.5×tan60°≈15.7.
解:作CE⊥AB,垂足分别为E、F.
(1)背水坡AD的坡度i=tanβ=1∶1.2= .
用计算器计算,得β≈39.8°.
E
F
D
C
B
A
G
H
K
在上题中,为了提高堤坝的 防洪能力,市防汛指挥部决定加固堤坝,要求坝顶CD加宽0.5米,背水坡AD的坡度改为1:1.4,已知堤坝的总长度为5㎞,求完成该项工程所需的土方(精确到0.1米3).
思考
如图是沿水库拦河坝的背水坡,将坡顶加宽2米,坡度由原来的1:2改为1:2.5,已知坝高6米,坝长50米.
求(1)加宽部分横断面AFEB的面积;
(2)完成这一工程需要多少土方?
练习1
E
F
D
C
B
A
G
H
A
B
C
D
如图,斜坡AC的坡度(坡比)为1:
AC=10米.坡顶有一旗杆BC,旗杆顶端B点
与A点有一条彩带AB相连,AB=14米.
试求旗杆BC的高度.
E
练习2
A
B
O
游乐场的大型摩天轮的半径为20m,旋转1周需要12min.小明乘坐最底部的车厢(离地面约0.5m)开始1周的观光,经过2min后,小明离地面的高度是多少?
C
D
1.摩天轮启动多长时间后,小明离
地面的高度将首次达到10?
2.小明将有多长时间连续保持在
离地面10m以上的空中?
问题2
解:如图,用⊙O表示摩天轮,A、B分别表示小明的出发点和2min后的到达点.由题意知,OB=20,∠BOA=360°÷6=60°.
作BC⊥OA,垂足为C.
在Rt△OCB中,
OC=OB·cos∠BOC=20×cos60°=20× =10,
AC=AO-CO=20-10=10.
因为摩天轮底部与地面相距0.3m,所以小明离地面的高度应为10.3m.
答:2min后小明离地面10.3m.
已知跷跷板长4m,当跷跷板的一端碰到地面
时,另一端离地面1.5m.求此时跷跷板与地面的夹角(精确到0.1°).
A
B
O
C
练习3
为了测量停留在空中的气球高度,小明在某处利用测角仪测得气球的仰角(从低处观测高处的目标时,视线与水平线所成的锐角)为27°,然后他沿气球方向前进了50m,再次测得仰角为40°.如果测角仪高度忽略不计, 那么气球的高度是多少(精确到0.1m)?
A
D
B
C
问题3
∵ AD-BD=50,
∴
∴
答:气球的高度约为64.9m.
解:如图,点A、B、C分别表示小明两次观测处及气球位置.由题意知,∠CAD=40°,CD⊥AD,AB=50m,设CD=xm.
在Rt△BCD中,
由tan40°= ,得BD=
在Rt△ADC中,由tan27°= ,得
如图,在一笔直的海岸线上有A,B两个观测站,A在B的正西方向,AB=2km,从A测得船C在北偏东60°的方向,从B测得船C在北偏西45°的方向.求船C离海岸线的距离.
A
B
C
2km
60°
45°
D
练习4
概念回顾
1.我们学过哪些三角函数?
2.还记得哪些特殊角的三角函数值?
3.勾股定理有哪些重要知识点?
【例题讲解】
1.如图,水坝的横截面是梯形ABCD,迎水坡BC的坡角为30°,背水坡AD的坡度为1:1.2,坝顶宽DC=2.5m,坝高4.5m.
求:(1)背水坡AD的坡角(精确到0.1°);
(2)坝底宽AB的长(精确到0.1m).
(2)在Rt△BEC中,
∠α=30°,∠BCE=90°-30°=60°,
EB=CE·tan∠BCE=4.5×tan60°.
在Rt△AFD中,
∵ =1∶1.2,
∴AF=1.2DF=1.2×4.5=5.4.
又FE=DC=2.5,
∴AB=AF+FE+EB=5.4+2.5+4.5×tan60°≈15.7.
解:作CE⊥AB,垂足分别为E、F.
(1)背水坡AD的坡度i=tanβ=1∶1.2= .
用计算器计算,得β≈39.8°.
思考:在上题中,为了提高堤坝的防洪能力,市防汛指挥部决定加固堤坝,要求坝顶CD加宽0.5m,背水坡AD的坡度改为1:1.4,已知堤坝的总长度为5km,求完成该项工程所需的土方(精确到0.1m3).
2.游乐场的大型摩天轮的半径为20m,旋转1周需要12min.小明从摩天轮的底部(与地面相距0.3m)出开始观光,2min后小明离地面多高?
【例题讲解】
解:如图,用⊙O表示摩天轮,A、B分别表示小明的出发点和2min后的到达点.由题意知,OB=20,∠BOA=360°÷6=60°.
作BC⊥OA,垂足为C.
在Rt△OCB中,
OC=OB·cos∠BOC=20×cos60°=20× =10,
AC=AO-CO=20-10=10.
因为摩天轮底部与地面相距0.3m,所以小明离地面的高度应为10.3m.
答:2min后小明离地面10.3m.
【拓展与延伸】
活动1 根据问题情境,完成下面的问题:
(1) 摩天轮转动多长时间后,小明离地面的高度将首次达到15.3m?
(2) 摩天轮转动一周,小明在离地面30.3m以上的空中有多长时间?
A
D
B
C
3.为了测量停留在空中的气球高度,小明在某处利用测角仪测得气球的仰角(从低处观测高处的目标时,视线与水平线所成的锐角)为27°,然后他沿气球方向前进了50m,再次测得仰角为40°.如果测角仪高度忽略不计, 那么气球的高度是多少(精确到0.1m)?
【例题讲解】
∵ AD-BD=50,
∴
∴
答:气球的高度约为64.9m.
解:如图,点A、B、C分别表示小明两次观测处及气球位置.由题意知,∠CAD=40°,CD⊥AD,AB=50m,设CD=xm.
在Rt△BCD中,
由tan40°= ,得BD=
在Rt△ADC中,由tan27°= ,得
1.在△ABC中,∠C=90°,∠A=45°,则BC∶AC∶AB = .
在△ABC中,∠C=90°,∠A=30°,则BC∶AC∶AB= .
2.在△ABC中,∠C=90°.
(1)已知∠A=30°,BC=8cm,求AB与AC的长;
(2)已知∠A=60°,AC=8cm,求AB与BC的长.
【练习】
3.如图所示,山坡上有一棵与水平面垂直的大树,一场台风过后,大树被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面.已知山坡的坡角 ∠BAC=38?,量得树干倾角∠AEF=23?,大树被折断部分和坡面所成的角∠ADC=60?,AD=4m.
(1)求∠CAE的度数;
(2)求这棵大树折断前的高度?(结果精确到个位,参考数据 , , ).
【练习】
4.单摆的摆长AB为90cm,当它摆动到AB′的位置时, ∠BAB′ =11°,问这时摆球B′A较最低点B升高了多少(精确到1cm)?
【练习】
5.如图,秋千链子的长度为3m,当秋千向两边摆动时,两边的摆动角度均为30?.求它摆动至最高位置与最低位置的高度之差(结果保留根号).
【练习】
谢谢聆听
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
