五年级下册数学课件 第九单元《第2课时 数与代数(2)》人教版 (共19张PPT)
文档属性
| 名称 | 五年级下册数学课件 第九单元《第2课时 数与代数(2)》人教版 (共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 749.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-20 09:32:04 | ||
图片预览






文档简介
第九单元
第2课时 数与代数(2)
人教版数学五年级下册
学习目标
1.进一步理解和掌握分数的意义及性质,并能解决一些问题,进一步理解同分母、异分母分数加、减法的算理,掌握同分母、异分母分数加、减法的计算方法。
2.能熟练地进行约分和通分,认识约分、通分的重要性。
同学们,这节课我们就一起来继续复习和整理一下关于数与代数的相关知识。
数与代数
导入新知
把单位“1”平均分成若干份,表示这样的1份或几份的数就是分数。
表示其中一份的数叫分数单位。
一个物体、一个计量单位,一些物体都可以看作一个整体,这个整体
可以用自然数1来表示,我们通常把它叫做单位“1”。
?
一、分数的意义
整体
14
?
重点解析
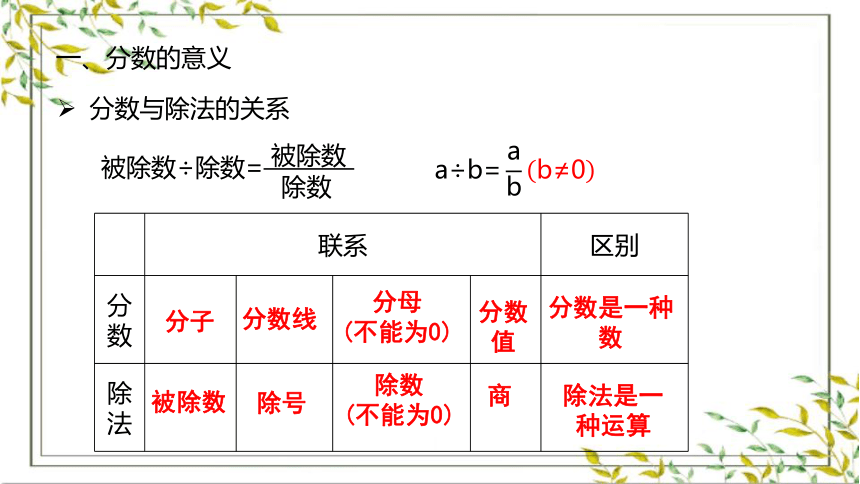
一、分数的意义
分数与除法的关系
被除数÷除数=????????????????????????
?
被除数
除数
a÷b=abb≠0
?
{5940675A-B579-460E-94D1-54222C63F5DA}
联系
区别
分数
除法
分数是一种数
除法是一种运算
分子
被除数
分数线
除号
分母
(不能为0)
除数
(不能为0)
分数
值
商
真分数:分子比分母小的分数叫做真分数。真分数小于1。
假分数:分子比分母大或分子和分母相等的分数叫做假分数。
假分数大于或等于1。
带分数:由整数(不包括0)和真分数合成的数叫做带分数。
假分数与带分数的互化方法:
二、真分数与假分数
整数分子分母
?
整数×分母+分子分母
?
(带分数)
(假分数)
三、分数的基本性质
分数的分子和分母同时乘或除以相同的数(0除外),分
数的大小不变。这叫做分数的基本性质。如
56=5×46×4=2024
?
1024=10÷224÷2=512
?
约分:把一个分数化成和它相等,但分子和分母都比较小的分数,叫做约分。
(1)逐次约分法;(2)一次约分法。
分子和分母只有公因数1的分数叫做最简分数。
三、分数的基本性质
通分:把异分母分数分别化成和原来分数相等的同分母分数,叫做通分。
通分选取分母的最小公倍数作为公分母进行通分。
将16与18通分。
?
16=424???18=324
?
四、分数和小数的互化
分数
小数
分数与小数互化
小数化成分数
A
分数化成小数
B
写成分母是10,100,1000,
…的分数,再化简。
用分子除以分母,除不尽时,要根据需要按“四舍五入”法保留几位小数。
五、分数加减法
同分母分数加减法:分母不变,只把分子相加、减。计算的结果能约
分的要约成最简分数。
715+ 615=7+615=1315
?
715? 615=7?615=115
?
异分母分数加减法:异分母分数相加、减,先通分,然后按照同分母
分数加、减法的计算方法进行计算。
310+14
?
=1120
?
=6+520
?
=620+520
?
五、分数加减法
分数加减混合运算:与整数加减混合运算
的运算顺序相同。
没有括号的,按照从左到右的顺序计算;
有括号的,先算括号里面的,再算括号外
面的。
整数运算定律在分数加法中同样适用。
1.填空。
58米表示把1米平均分成( )份,取其中( )份的数;也可以表示把5米平均分成( )份,取其中( )份的数。
分母是4的真分数:( ),分子是4的假分数:( )。
一张彩纸,第一次用去它的38?,第二次用去它的15?,两次一共用去这张彩纸的( )。
?
8
5
8
1
14、24、 34
?
41、42、 43、44
?
2340?
?
课堂练习
14
5
7
4
=
+
14
3
3
1
12
7
7
4
7
3
+
=
1
9
4
9
7
-
=
4
1
3
1
+
=
3
2
6
5
-
=
6
1
5
1
4
1
-
=
20
1
2.
3.分数加减混合运算
2
-
12
3
12
+
6
12
=
2
12
-
9
12
=
7
12
=
2
1
+
6
5
-
( )
3
1
6
1
4
1
-
2
1
+
5
6
=
-
6
5
0
=
-
( )
5
6
=
+
6
3
6
2
4.用简便方法计算
19?110+ 89
?
815+16+715+ 56
?
= 19+ 89- 110
?
= 1- 110
?
= 910
?
=( 815+ 715?)+( 16+ 56?)
?
= 1+1
?
=2
5.五(1)班采集树种,第一组采集89kg,比第二组多采集了15?kg,第二组比第三组少采集了19?kg。第三组采集树种多少千克?
?
89- 15+ 19
?
= 89+ 19- 15
?
答:第三组采集树种45千克。
?
= 45(千克)
?
6.某农场进行喷洒农药作业,第一天喷洒了一块地的14?,第二天比第一天多喷洒了这块地的110?。还剩这块地的几分之几没有喷洒农药?
?
1?(14+ 110+ 14)
?
= 1- 35
?
答:还剩这块地的25没有喷洒农药。
?
= 25
?
7.张师傅加工一批服装,上半月完成计划的58?,下半月完成计划的35?。这个月超额完成计划的几分之几?
?
58+ 35?1
?
= 4940?1
?
答:这个月超额完成计划的940。
?
= 940
?
再 见
第2课时 数与代数(2)
人教版数学五年级下册
学习目标
1.进一步理解和掌握分数的意义及性质,并能解决一些问题,进一步理解同分母、异分母分数加、减法的算理,掌握同分母、异分母分数加、减法的计算方法。
2.能熟练地进行约分和通分,认识约分、通分的重要性。
同学们,这节课我们就一起来继续复习和整理一下关于数与代数的相关知识。
数与代数
导入新知
把单位“1”平均分成若干份,表示这样的1份或几份的数就是分数。
表示其中一份的数叫分数单位。
一个物体、一个计量单位,一些物体都可以看作一个整体,这个整体
可以用自然数1来表示,我们通常把它叫做单位“1”。
?
一、分数的意义
整体
14
?
重点解析
一、分数的意义
分数与除法的关系
被除数÷除数=????????????????????????
?
被除数
除数
a÷b=abb≠0
?
{5940675A-B579-460E-94D1-54222C63F5DA}
联系
区别
分数
除法
分数是一种数
除法是一种运算
分子
被除数
分数线
除号
分母
(不能为0)
除数
(不能为0)
分数
值
商
真分数:分子比分母小的分数叫做真分数。真分数小于1。
假分数:分子比分母大或分子和分母相等的分数叫做假分数。
假分数大于或等于1。
带分数:由整数(不包括0)和真分数合成的数叫做带分数。
假分数与带分数的互化方法:
二、真分数与假分数
整数分子分母
?
整数×分母+分子分母
?
(带分数)
(假分数)
三、分数的基本性质
分数的分子和分母同时乘或除以相同的数(0除外),分
数的大小不变。这叫做分数的基本性质。如
56=5×46×4=2024
?
1024=10÷224÷2=512
?
约分:把一个分数化成和它相等,但分子和分母都比较小的分数,叫做约分。
(1)逐次约分法;(2)一次约分法。
分子和分母只有公因数1的分数叫做最简分数。
三、分数的基本性质
通分:把异分母分数分别化成和原来分数相等的同分母分数,叫做通分。
通分选取分母的最小公倍数作为公分母进行通分。
将16与18通分。
?
16=424???18=324
?
四、分数和小数的互化
分数
小数
分数与小数互化
小数化成分数
A
分数化成小数
B
写成分母是10,100,1000,
…的分数,再化简。
用分子除以分母,除不尽时,要根据需要按“四舍五入”法保留几位小数。
五、分数加减法
同分母分数加减法:分母不变,只把分子相加、减。计算的结果能约
分的要约成最简分数。
715+ 615=7+615=1315
?
715? 615=7?615=115
?
异分母分数加减法:异分母分数相加、减,先通分,然后按照同分母
分数加、减法的计算方法进行计算。
310+14
?
=1120
?
=6+520
?
=620+520
?
五、分数加减法
分数加减混合运算:与整数加减混合运算
的运算顺序相同。
没有括号的,按照从左到右的顺序计算;
有括号的,先算括号里面的,再算括号外
面的。
整数运算定律在分数加法中同样适用。
1.填空。
58米表示把1米平均分成( )份,取其中( )份的数;也可以表示把5米平均分成( )份,取其中( )份的数。
分母是4的真分数:( ),分子是4的假分数:( )。
一张彩纸,第一次用去它的38?,第二次用去它的15?,两次一共用去这张彩纸的( )。
?
8
5
8
1
14、24、 34
?
41、42、 43、44
?
2340?
?
课堂练习
14
5
7
4
=
+
14
3
3
1
12
7
7
4
7
3
+
=
1
9
4
9
7
-
=
4
1
3
1
+
=
3
2
6
5
-
=
6
1
5
1
4
1
-
=
20
1
2.
3.分数加减混合运算
2
-
12
3
12
+
6
12
=
2
12
-
9
12
=
7
12
=
2
1
+
6
5
-
( )
3
1
6
1
4
1
-
2
1
+
5
6
=
-
6
5
0
=
-
( )
5
6
=
+
6
3
6
2
4.用简便方法计算
19?110+ 89
?
815+16+715+ 56
?
= 19+ 89- 110
?
= 1- 110
?
= 910
?
=( 815+ 715?)+( 16+ 56?)
?
= 1+1
?
=2
5.五(1)班采集树种,第一组采集89kg,比第二组多采集了15?kg,第二组比第三组少采集了19?kg。第三组采集树种多少千克?
?
89- 15+ 19
?
= 89+ 19- 15
?
答:第三组采集树种45千克。
?
= 45(千克)
?
6.某农场进行喷洒农药作业,第一天喷洒了一块地的14?,第二天比第一天多喷洒了这块地的110?。还剩这块地的几分之几没有喷洒农药?
?
1?(14+ 110+ 14)
?
= 1- 35
?
答:还剩这块地的25没有喷洒农药。
?
= 25
?
7.张师傅加工一批服装,上半月完成计划的58?,下半月完成计划的35?。这个月超额完成计划的几分之几?
?
58+ 35?1
?
= 4940?1
?
答:这个月超额完成计划的940。
?
= 940
?
再 见
