6.3 同底数幂的除法 课件(共16张PPT)
文档属性
| 名称 | 6.3 同底数幂的除法 课件(共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-20 07:53:39 | ||
图片预览






文档简介
第六章 整式的乘除
3 同底数幂的除法
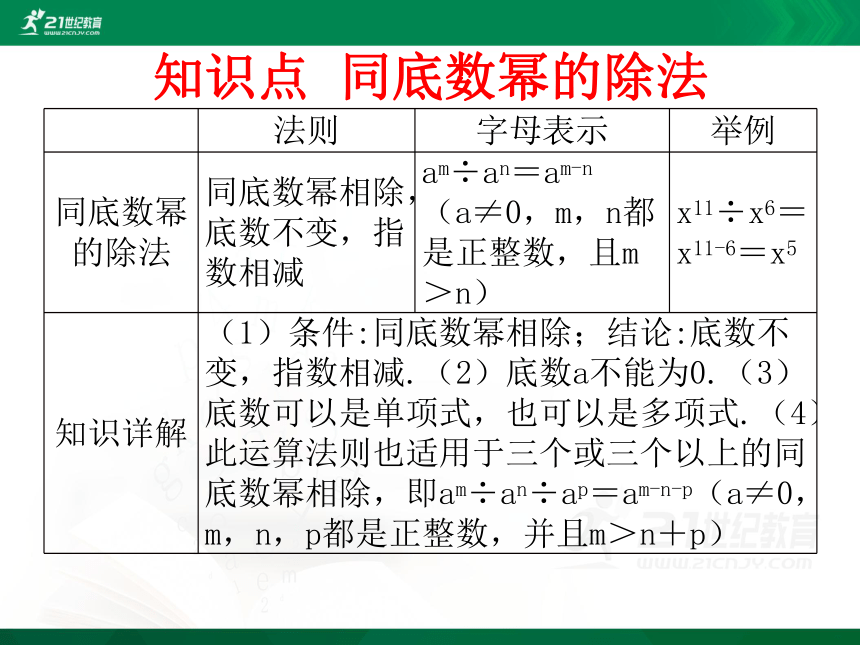
知识点 同底数幂的除法
法则
字母表示
举例
同底数幂的除法
知识详解
知识点 同底数幂的除法
法则
字母表示
举例
同底数幂的除法
同底数幂相除,底数不变,指数相减
am÷an=am-n(a≠0,m,n都是正整数,且m>n)
x11÷x6=x11-6=x5
知识详解
(1)条件:同底数幂相除;结论:底数不变,指数相减.(2)底数a不能为0.(3)底数可以是单项式,也可以是多项式.(4)此运算法则也适用于三个或三个以上的同底数幂相除,即am÷an÷ap=am-n-p(a≠0,m,n,p都是正整数,并且m>n+p)
例 计算:(1)x8÷x3;(2)(-a)5÷(-a)2;
(3)(-xy)6÷(-xy);(4)(2x3)7÷(2x3)5;
(5)(x-y)7÷(x-y)6.
例 计算:(1)x8÷x3;(2)(-a)5÷(-a)2;
(3)(-xy)6÷(-xy);(4)(2x3)7÷(2x3)5;
(5)(x-y)7÷(x-y)6.
解析 (1)x8÷x3=x8-3=x5.
(2)(-a)5÷(-a)2=(-a)5-2=(-a)3=-a3.(3)(-xy)6÷(-xy)=(-xy)6-1=(-xy)5=-x5y5.
(4)(2x3)7÷(2x3)5=(2x3)7-5=(2x3)2=4x6.
(5)(x-y)7÷(x-y)6=(x-y)7-6 =x-y.
经典例题
题型一 幂的混合运算
例1 计算:(1)m4·m5+m10÷m-(m3)3;
(2)x5·x3-(2x4)2+x10÷x2.
题型一 幂的混合运算
例1 计算:(1)m4·m5+m10÷m-(m3)3;
(2)x5·x3-(2x4)2+x10÷x2.
解析 (1)原式=m9+m9-m9=m9.
(2)原式=x8-4x8+x8=-2x8.
题型一 幂的混合运算
例1 计算:(1)m4·m5+m10÷m-(m3)3;
(2)x5·x3-(2x4)2+x10÷x2.
解析 (1)原式=m9+m9-m9=m9.
(2)原式=x8-4x8+x8=-2x8.
点拨 解题时应先分清是哪种运算,若是同底数幂相乘,则将指数相加;若是同底数幂相除,则将指数相减;若是幂的乘方,则将指数相乘.
题型二 同底数幂的除法法则的逆用
例2 已知10a=5,10b=6,求102a+3b-2的值.
题型二 同底数幂的除法法则的逆用
例2 已知10a=5,10b=6,求102a+3b-2的值.
解析 因为10a=5,10b=6,
所以102a+3b-2=(10a)2·(10b)3÷102
=52×63÷100=25×216÷100=54.
题型二 同底数幂的除法法则的逆用
例2 已知10a=5,10b=6,求102a+3b-2的值.
解析 因为10a=5,10b=6,
所以102a+3b-2=(10a)2·(10b)3÷102
=52×63÷100=25×216÷100=54.
点拨
当遇到幂的指数是差的形式时,为了计算需要,往往逆用同底数幂的除法法则,将幂转化成几个同底数幂的除法.但是一定要注意,转化后指数的差仍等于原指数.
易错易混
易错点 忽略没有指数的字母的指数
例 计算:(-a)3÷a.
易错点 忽略没有指数的字母的指数
例 计算:(-a)3÷a.
错解 原式=-a3÷a=-a3.
正解 (-a)3÷a=-a3÷a=-a3-1=-a2.
易错点 忽略没有指数的字母的指数
例 计算:(-a)3÷a.
错解 原式=-a3÷a=-a3.
正解 (-a)3÷a=-a3÷a=-a3-1=-a2.
错因分析 误认为a的指数为0,导致出错.
3 同底数幂的除法
知识点 同底数幂的除法
法则
字母表示
举例
同底数幂的除法
知识详解
知识点 同底数幂的除法
法则
字母表示
举例
同底数幂的除法
同底数幂相除,底数不变,指数相减
am÷an=am-n(a≠0,m,n都是正整数,且m>n)
x11÷x6=x11-6=x5
知识详解
(1)条件:同底数幂相除;结论:底数不变,指数相减.(2)底数a不能为0.(3)底数可以是单项式,也可以是多项式.(4)此运算法则也适用于三个或三个以上的同底数幂相除,即am÷an÷ap=am-n-p(a≠0,m,n,p都是正整数,并且m>n+p)
例 计算:(1)x8÷x3;(2)(-a)5÷(-a)2;
(3)(-xy)6÷(-xy);(4)(2x3)7÷(2x3)5;
(5)(x-y)7÷(x-y)6.
例 计算:(1)x8÷x3;(2)(-a)5÷(-a)2;
(3)(-xy)6÷(-xy);(4)(2x3)7÷(2x3)5;
(5)(x-y)7÷(x-y)6.
解析 (1)x8÷x3=x8-3=x5.
(2)(-a)5÷(-a)2=(-a)5-2=(-a)3=-a3.(3)(-xy)6÷(-xy)=(-xy)6-1=(-xy)5=-x5y5.
(4)(2x3)7÷(2x3)5=(2x3)7-5=(2x3)2=4x6.
(5)(x-y)7÷(x-y)6=(x-y)7-6 =x-y.
经典例题
题型一 幂的混合运算
例1 计算:(1)m4·m5+m10÷m-(m3)3;
(2)x5·x3-(2x4)2+x10÷x2.
题型一 幂的混合运算
例1 计算:(1)m4·m5+m10÷m-(m3)3;
(2)x5·x3-(2x4)2+x10÷x2.
解析 (1)原式=m9+m9-m9=m9.
(2)原式=x8-4x8+x8=-2x8.
题型一 幂的混合运算
例1 计算:(1)m4·m5+m10÷m-(m3)3;
(2)x5·x3-(2x4)2+x10÷x2.
解析 (1)原式=m9+m9-m9=m9.
(2)原式=x8-4x8+x8=-2x8.
点拨 解题时应先分清是哪种运算,若是同底数幂相乘,则将指数相加;若是同底数幂相除,则将指数相减;若是幂的乘方,则将指数相乘.
题型二 同底数幂的除法法则的逆用
例2 已知10a=5,10b=6,求102a+3b-2的值.
题型二 同底数幂的除法法则的逆用
例2 已知10a=5,10b=6,求102a+3b-2的值.
解析 因为10a=5,10b=6,
所以102a+3b-2=(10a)2·(10b)3÷102
=52×63÷100=25×216÷100=54.
题型二 同底数幂的除法法则的逆用
例2 已知10a=5,10b=6,求102a+3b-2的值.
解析 因为10a=5,10b=6,
所以102a+3b-2=(10a)2·(10b)3÷102
=52×63÷100=25×216÷100=54.
点拨
当遇到幂的指数是差的形式时,为了计算需要,往往逆用同底数幂的除法法则,将幂转化成几个同底数幂的除法.但是一定要注意,转化后指数的差仍等于原指数.
易错易混
易错点 忽略没有指数的字母的指数
例 计算:(-a)3÷a.
易错点 忽略没有指数的字母的指数
例 计算:(-a)3÷a.
错解 原式=-a3÷a=-a3.
正解 (-a)3÷a=-a3÷a=-a3-1=-a2.
易错点 忽略没有指数的字母的指数
例 计算:(-a)3÷a.
错解 原式=-a3÷a=-a3.
正解 (-a)3÷a=-a3÷a=-a3-1=-a2.
错因分析 误认为a的指数为0,导致出错.
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
