2020--2021学年人教版七年级数学下册6.2《立方根》教学课件(20张)
文档属性
| 名称 | 2020--2021学年人教版七年级数学下册6.2《立方根》教学课件(20张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-19 23:55:42 | ||
图片预览








文档简介
(共20张PPT)
第六章
实数
6.2
立方根
学习目标
1.了解立方根和开立方的概念,掌握立方根的性质.
2.会用根号表示一个数的立方根.
3.能用开立方运算求数的立方根,体会立方与开立方运算的互逆性.
1.什么叫平方根?如何用符号表示数a(a≥0)的平方根?
一般地,如果一个正数x的平方等于a,即x2=a,那么这个正数x叫做a的算术平方根.
正数a的平方根是:±
课堂导入
(1)正数的平方根有两个,它们互为相反数;
(2)0的平方根是0;
(3)负数没有平方根.
2.平方根具有什么特征?
复习:
1.立方根
新知讲解
解:设这种包装箱的棱长为xm,
则x3=27.
因为33=27,所以x=3.
如果一个数的立方等于,即
,那么这个数叫做的立方根(也叫作的三次方根).
要制作一种容积为27m3
的正方体形状的包装箱,这种包装箱的棱长应该是多少?
叫做的立方根;
叫做的立方根;
0叫做的立方根.
新知讲解
如果x3=a,那么x叫做a的立方根.
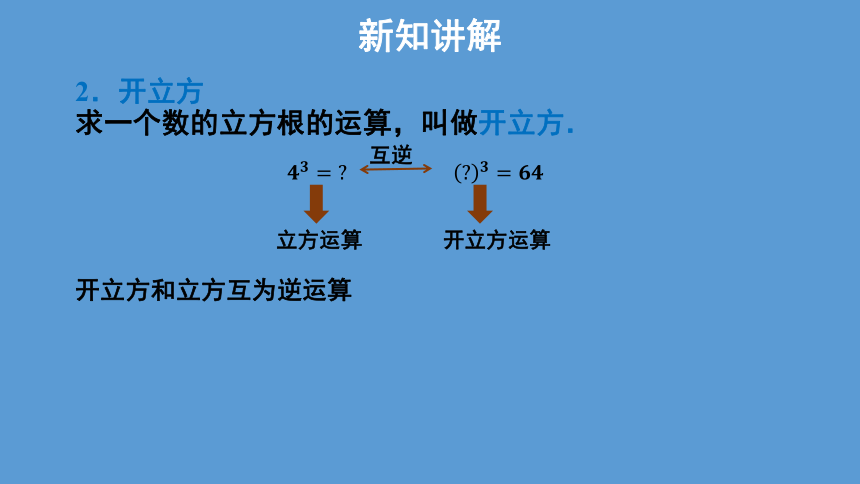
2.开立方
新知讲解
由题意可得x3=a,
要求x的值,那么就要把x的指数3去掉,这个过程就是开立方的过程.
等式的左边开立方,那么右边也需要开立方,
想一想:如果知道了一个数为a,那么怎么求它的立方根?
分析:设:数x的立方为a,那么求x的值.
即,所以x
2.开立方
求一个数的立方根的运算,叫做开立方.
立方运算
开立方运算
互逆
开立方和立方互为逆运算
新知讲解
3.立方根的表示方法
例如的立
方根表示为,
(1)一个数a的立方根表示为“”,读作“三次根号”.
根指数
被开方数
9的立
方根表示为.,
的立
方根表示为.
提示中根指数不能省略.
新知讲解
(2)探究连续开立方问题.
要求观看动画,探究连续开立方问题,通过对被开方数进行分类,实现连续开立方运算,进而通过结果总结规律..
新知讲解
4.立方根的性质
新知讲解
每一个数都有立方根吗?
一个数有几个立方根呢?
每个数都有立方根.
一个数有1个立方根
开立方数包括正数,零,负数.
的立方根是;
的立方根为.
的立方根是;
立方根的性质:
正数的立方根是正数;
负数的立方根是负数;
0的立方根是0.
5.立方根小数点移动法则
提示:被开方数的小数点移动的位数必须是的倍数.
新知讲解
实际上,很多有理数的立方根是无限不循环小数,如
,
等都是无限不循环小数.
要求一个数的立方根(或近似值),我们可以利用计算器的
键来计算.
5.立方根小数点移动法则
新知讲解
探究规律:
观察动画,通过先观察再练习的方式,探究得到立方根小数点位数移动规律.
用计算器计算动画中的数值,并发现规律:
被开立方的数的小数点每向右(或向左)移动三位,它的立方根的小数点就向右(或向左)移动一位.
6.平方根与立方根有什么不同?
新知讲解
出示图片:从不同角度对比平方根与立方根,加深对概念的理解.
【例题1】?下列说法正确的是(
)
①是的立方根;
②的立方根是;
③是的立方根;
④
的立方根是.
A.个
B.2个
C.3个
D.4个
A
分析:
①
②
③
④
不正确
不正确
,
立方的根是
不正确
的立方根是.
正确
的立方根是
.
新知讲解
【例题2】填空:
①立方根等于它本身的数是_________________;
②平方根与立方根相等的数是_______________;
③算术平方根和立方根相等的数是___________;
分析:
,,.
.
①
②
,1和-1
和
=.
③
新知讲解
【例题3】已知2m-27的立方根是,求的平方根.
解:
∵,
∴,
∴
.
∴,
∴的平方根是.
新知讲解
1.若一个数的平方根与这个数的立方根互为相反数,则这个数是( )
A.?-1
B.?0
C.?±1
D.?不存在
2.
的算术平方根是______?;的立方根是________;的平方根是_______?;若x2=,则x=_______;
如果=3,那么?.
3.若=0.7160,
=1.542,
则=________?,=_______.
7.160
-0.07160?
随堂练习
4.已知:M=
是m+3的算术平方根,
是n-2的立方根,试求(M-N)2.
由题意得,,
解:
解得
,
∴M=
,
∴(M-N)2=
随堂练习
开立方:求一个数的立方根的运算,叫做开立方.开立方与立方也是互为逆运算.
立方根:一般地,如果一个数的立方等于a,这个数就叫做a的立方根(也叫做三次方根).
如果x3=a,那么x叫做a的立方根.
立方根的性质:一个正数的立方根只有一个,即正数的立方根是正数,负数的立方根是负数,0的立方根是0.
课堂小结
再见
第六章
实数
6.2
立方根
学习目标
1.了解立方根和开立方的概念,掌握立方根的性质.
2.会用根号表示一个数的立方根.
3.能用开立方运算求数的立方根,体会立方与开立方运算的互逆性.
1.什么叫平方根?如何用符号表示数a(a≥0)的平方根?
一般地,如果一个正数x的平方等于a,即x2=a,那么这个正数x叫做a的算术平方根.
正数a的平方根是:±
课堂导入
(1)正数的平方根有两个,它们互为相反数;
(2)0的平方根是0;
(3)负数没有平方根.
2.平方根具有什么特征?
复习:
1.立方根
新知讲解
解:设这种包装箱的棱长为xm,
则x3=27.
因为33=27,所以x=3.
如果一个数的立方等于,即
,那么这个数叫做的立方根(也叫作的三次方根).
要制作一种容积为27m3
的正方体形状的包装箱,这种包装箱的棱长应该是多少?
叫做的立方根;
叫做的立方根;
0叫做的立方根.
新知讲解
如果x3=a,那么x叫做a的立方根.
2.开立方
新知讲解
由题意可得x3=a,
要求x的值,那么就要把x的指数3去掉,这个过程就是开立方的过程.
等式的左边开立方,那么右边也需要开立方,
想一想:如果知道了一个数为a,那么怎么求它的立方根?
分析:设:数x的立方为a,那么求x的值.
即,所以x
2.开立方
求一个数的立方根的运算,叫做开立方.
立方运算
开立方运算
互逆
开立方和立方互为逆运算
新知讲解
3.立方根的表示方法
例如的立
方根表示为,
(1)一个数a的立方根表示为“”,读作“三次根号”.
根指数
被开方数
9的立
方根表示为.,
的立
方根表示为.
提示中根指数不能省略.
新知讲解
(2)探究连续开立方问题.
要求观看动画,探究连续开立方问题,通过对被开方数进行分类,实现连续开立方运算,进而通过结果总结规律..
新知讲解
4.立方根的性质
新知讲解
每一个数都有立方根吗?
一个数有几个立方根呢?
每个数都有立方根.
一个数有1个立方根
开立方数包括正数,零,负数.
的立方根是;
的立方根为.
的立方根是;
立方根的性质:
正数的立方根是正数;
负数的立方根是负数;
0的立方根是0.
5.立方根小数点移动法则
提示:被开方数的小数点移动的位数必须是的倍数.
新知讲解
实际上,很多有理数的立方根是无限不循环小数,如
,
等都是无限不循环小数.
要求一个数的立方根(或近似值),我们可以利用计算器的
键来计算.
5.立方根小数点移动法则
新知讲解
探究规律:
观察动画,通过先观察再练习的方式,探究得到立方根小数点位数移动规律.
用计算器计算动画中的数值,并发现规律:
被开立方的数的小数点每向右(或向左)移动三位,它的立方根的小数点就向右(或向左)移动一位.
6.平方根与立方根有什么不同?
新知讲解
出示图片:从不同角度对比平方根与立方根,加深对概念的理解.
【例题1】?下列说法正确的是(
)
①是的立方根;
②的立方根是;
③是的立方根;
④
的立方根是.
A.个
B.2个
C.3个
D.4个
A
分析:
①
②
③
④
不正确
不正确
,
立方的根是
不正确
的立方根是.
正确
的立方根是
.
新知讲解
【例题2】填空:
①立方根等于它本身的数是_________________;
②平方根与立方根相等的数是_______________;
③算术平方根和立方根相等的数是___________;
分析:
,,.
.
①
②
,1和-1
和
=.
③
新知讲解
【例题3】已知2m-27的立方根是,求的平方根.
解:
∵,
∴,
∴
.
∴,
∴的平方根是.
新知讲解
1.若一个数的平方根与这个数的立方根互为相反数,则这个数是( )
A.?-1
B.?0
C.?±1
D.?不存在
2.
的算术平方根是______?;的立方根是________;的平方根是_______?;若x2=,则x=_______;
如果=3,那么?.
3.若=0.7160,
=1.542,
则=________?,=_______.
7.160
-0.07160?
随堂练习
4.已知:M=
是m+3的算术平方根,
是n-2的立方根,试求(M-N)2.
由题意得,,
解:
解得
,
∴M=
,
∴(M-N)2=
随堂练习
开立方:求一个数的立方根的运算,叫做开立方.开立方与立方也是互为逆运算.
立方根:一般地,如果一个数的立方等于a,这个数就叫做a的立方根(也叫做三次方根).
如果x3=a,那么x叫做a的立方根.
立方根的性质:一个正数的立方根只有一个,即正数的立方根是正数,负数的立方根是负数,0的立方根是0.
课堂小结
再见
