2020-2021学年苏教版九年级下学期第7章《锐角三角函数》单元测试题(Word版 含部分答案)
文档属性
| 名称 | 2020-2021学年苏教版九年级下学期第7章《锐角三角函数》单元测试题(Word版 含部分答案) |  | |
| 格式 | doc | ||
| 文件大小 | 202.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-19 23:58:13 | ||
图片预览

文档简介
《三角函数》全章综合测试
一、单选题(每题3分,共30分)
1. 已知是一个锐角,下列关于的说法中,错误的是( )
A. cos会随着的增大而增大 B. 表示角的余弦值
C. cos表示在直角三角形中,角的邻边与斜边之比
D. 对于任意的锐角,必定有0 < cos< 1
2. 如图,在△ABC中,∠C=90°,设∠A,∠B,∠C所对的边分别为
a,b,c,则( )
A.c = b sin B B.b= c sin B
C.a = b tan B D.b = c tan B
3. 如图,测角仪CD竖直放在距建筑物AB底部5m的位置,在D处测得建筑物顶端A的仰角为50°.若测角仪的高度是1.5m,则建筑物AB的高度约为( )米
(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19)
A. 4.5 B. 6 C. 7.5 D. 10.5
4. 如图,在4×5的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在正方形网格的格点上,那么sin∠ACB的值为( )
A. B. C. D.
5. 如图,数学活动小组利用测角仪和皮尺测量学校旗杆的高度,在点D处测得旗杆顶端A的仰角∠ADE为55°,测角仪CD的高度为1米,其底端C与旗杆底端B之间的距离为6米,设旗杆AB的高度为x米,则下列关系式正确的是( )
A. tan55°= B. tan55°=
C. sin55°= D. cos55°=
6. 如图,为了测量一条河流的宽度,一测量员在河岸边相距200米的P、Q两点分别测定对岸一棵树T的位置,T在P的正北方向,且T在Q的北偏西70°方向,则河宽(PT的长)可以表示为( )米
A. 200 tan70° B.
C. 200sin70° D.
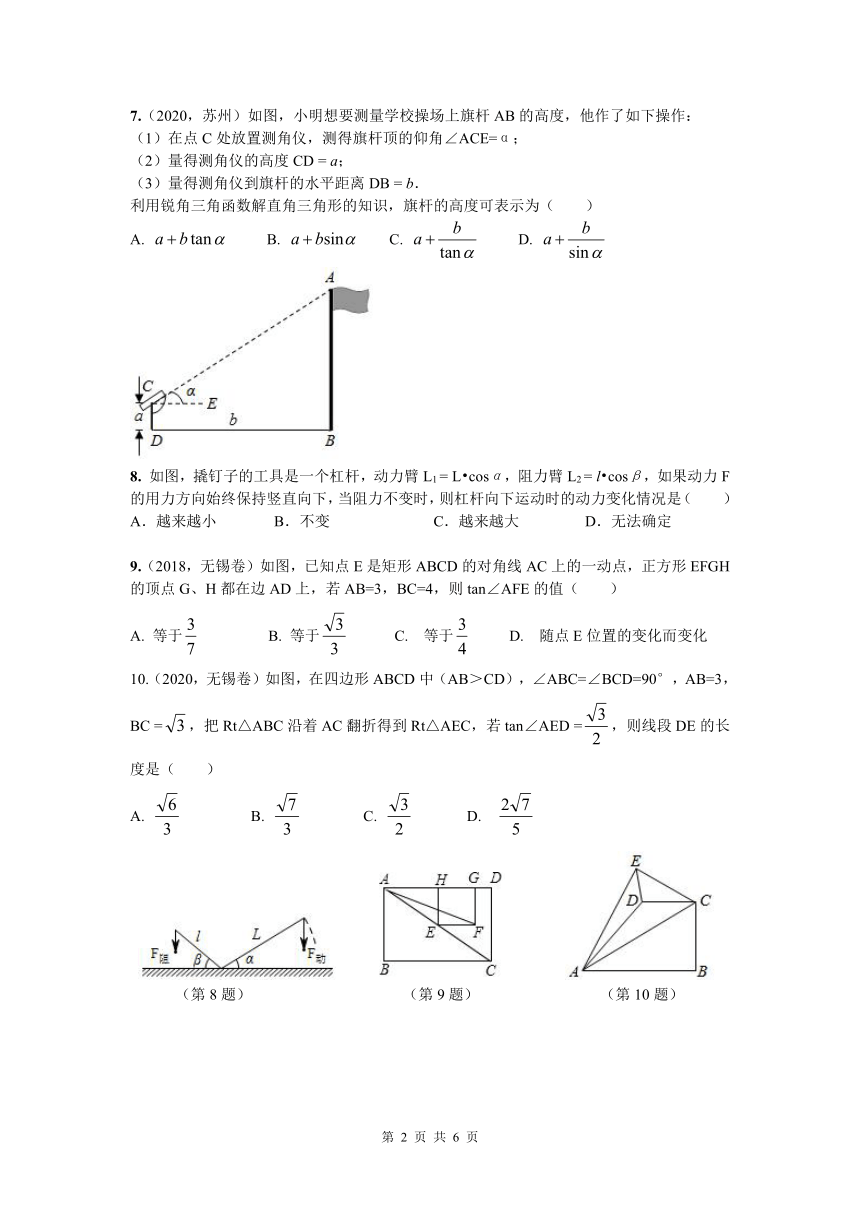
7.(2020,苏州)如图,小明想要测量学校操场上旗杆AB的高度,他作了如下操作:
(1)在点C处放置测角仪,测得旗杆顶的仰角∠ACE=α;
(2)量得测角仪的高度CD = a;
(3)量得测角仪到旗杆的水平距离DB = b.
利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为( )
A. B. C. D.
8. 如图,撬钉子的工具是一个杠杆,动力臂L1 = L?cosα,阻力臂L2 = l?cosβ,如果动力F的用力方向始终保持竖直向下,当阻力不变时,则杠杆向下运动时的动力变化情况是( )
A.越来越小 B.不变 C.越来越大 D.无法确定
9.(2018,无锡卷)如图,已知点E是矩形ABCD的对角线AC上的一动点,正方形EFGH的顶点G、H都在边AD上,若AB=3,BC=4,则tan∠AFE的值( )
A. 等于 B. 等于 C. 等于 D. 随点E位置的变化而变化
10.(2020,无锡卷)如图,在四边形ABCD中(AB>CD),∠ABC=∠BCD=90°,AB=3,BC =,把Rt△ABC沿着AC翻折得到Rt△AEC,若tan∠AED =,则线段DE的长度是( )
A. B. C. D.
(第8题) (第9题) (第10题)
二、填空题(每题2分,共16分)
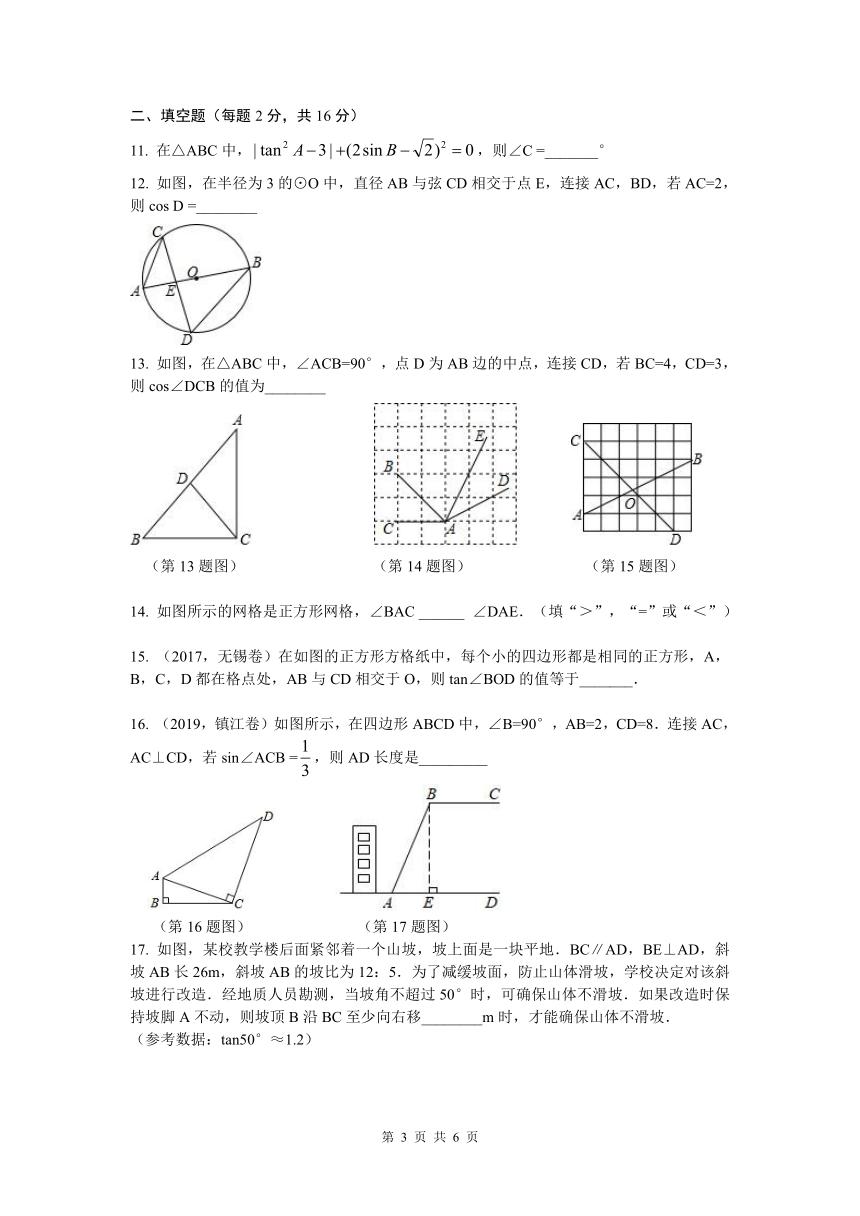
11. 在△ABC中,,则∠C =_______°
12. 如图,在半径为3的⊙O中,直径AB与弦CD相交于点E,连接AC,BD,若AC=2,则cos D =________
13. 如图,在△ABC中,∠ACB=90°,点D为AB边的中点,连接CD,若BC=4,CD=3,则cos∠DCB的值为________
(第13题图) (第14题图) (第15题图)
14. 如图所示的网格是正方形网格,∠BAC ______ ∠DAE.(填“>”,“=”或“<”)
15. (2017,无锡卷)在如图的正方形方格纸中,每个小的四边形都是相同的正方形,A,B,C,D都在格点处,AB与CD相交于O,则tan∠BOD的值等于_______.
16. (2019,镇江卷)如图所示,在四边形ABCD中,∠B=90°,AB=2,CD=8.连接AC,AC⊥CD,若sin∠ACB =,则AD长度是_________
(第16题图) (第17题图)
17. 如图,某校教学楼后面紧邻着一个山坡,坡上面是一块平地.BC∥AD,BE⊥AD,斜坡AB长26m,斜坡AB的坡比为12:5.为了减缓坡面,防止山体滑坡,学校决定对该斜坡进行改造.经地质人员勘测,当坡角不超过50°时,可确保山体不滑坡.如果改造时保持坡脚A不动,则坡顶B沿BC至少向右移________m时,才能确保山体不滑坡.
(参考数据:tan50°≈1.2)
18.(2019,宿迁)如图,∠MAN=60°,若△ABC的顶点B在射线AM上,且AB=2,点C在射线AN上运动,当△ABC是锐角三角形时,BC的取值范围是_________
三、计算题(每题8分,共16分)
19. 如图,在Rt△ABC中,∠ACB=90°,AC=BC=3,点D在边AC上,且AD=2CD,DE⊥AB,垂足为点E,连接CE,求:
(1)线段BE的长;
(2)∠ECB的正切值.
20. 已知△ABC中,AB = 10,AC = 2,∠B=30°,求△ABC的面积。
(改编自2018年无锡中考数学卷第17题)
四、解答题(共38分)
21. (本题满分6分)如图,楼房AB建在山坡BC上,其坡度为i =1:2,小明从山坡底部C处测得点A的仰角为56.35°,已知山坡的高度BD为10米,求楼房AB的高.
(结果精确到1米)(注:坡度i是指坡面的铅直高度BD与水平宽度CD的比)
参考数据:sin56.35°≈ 0.83,cos56.35° ≈ 0.55,tan56.35° ≈ 1.50
22. (本题满分6分)如图,要在原始森林附近修一条公路MN,已知C点周围260米范围内为原始森林保护区,在M上的点A处测得C在A的东北方向上(即∠DAC=45°),从A向东走800米到达B处,测得C在点B的北偏西60°方向上,MN是否穿过原始森林保护区,为什么?(结果精确到个位,参考数据:)
23. (本题满分8分)如图,在Rt△ABC中,∠C=90°,AD是△ABC的角平分线,点O在边AB上.过点A、D的圆的圆心O在边AB上,它与边AB交于另一点E.
(1)试判断BC与圆O的位置关系,并说明理由;
(2)若AC = 6,sin B =,求AD的长。
24. (本题满分8分)如图,四边形ABCD内接于⊙O,AB=17,CD=10,∠A=90°,
cos B =,求AD的长.
25. (本题10分)如图,某数学兴趣小组为测量一棵古树BH和教学楼CG的高,先在A处用高2米的测角仪测得古树顶端H的仰角∠HDE为45°,此时教学楼顶端G恰好在视线DH上,再向前走6米到达B处,又测得教学楼顶端G的仰角∠GEF为60°,点A、B、C三点在同一水平线上.
(1)计算古树BH的高;
(2)计算教学楼CG的高.(结果保留根号)
【简明参考答案】
1~10 A B C D B B A A A B
11. 75° 12. 13. 14. >
15. 3 16. 10 17. 10 18.
19.(1)BE = (2)tan∠ECB = 2
20. 15 或 (分类讨论三角形的形状)
一、单选题(每题3分,共30分)
1. 已知是一个锐角,下列关于的说法中,错误的是( )
A. cos会随着的增大而增大 B. 表示角的余弦值
C. cos表示在直角三角形中,角的邻边与斜边之比
D. 对于任意的锐角,必定有0 < cos< 1
2. 如图,在△ABC中,∠C=90°,设∠A,∠B,∠C所对的边分别为
a,b,c,则( )
A.c = b sin B B.b= c sin B
C.a = b tan B D.b = c tan B
3. 如图,测角仪CD竖直放在距建筑物AB底部5m的位置,在D处测得建筑物顶端A的仰角为50°.若测角仪的高度是1.5m,则建筑物AB的高度约为( )米
(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19)
A. 4.5 B. 6 C. 7.5 D. 10.5
4. 如图,在4×5的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在正方形网格的格点上,那么sin∠ACB的值为( )
A. B. C. D.
5. 如图,数学活动小组利用测角仪和皮尺测量学校旗杆的高度,在点D处测得旗杆顶端A的仰角∠ADE为55°,测角仪CD的高度为1米,其底端C与旗杆底端B之间的距离为6米,设旗杆AB的高度为x米,则下列关系式正确的是( )
A. tan55°= B. tan55°=
C. sin55°= D. cos55°=
6. 如图,为了测量一条河流的宽度,一测量员在河岸边相距200米的P、Q两点分别测定对岸一棵树T的位置,T在P的正北方向,且T在Q的北偏西70°方向,则河宽(PT的长)可以表示为( )米
A. 200 tan70° B.
C. 200sin70° D.
7.(2020,苏州)如图,小明想要测量学校操场上旗杆AB的高度,他作了如下操作:
(1)在点C处放置测角仪,测得旗杆顶的仰角∠ACE=α;
(2)量得测角仪的高度CD = a;
(3)量得测角仪到旗杆的水平距离DB = b.
利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为( )
A. B. C. D.
8. 如图,撬钉子的工具是一个杠杆,动力臂L1 = L?cosα,阻力臂L2 = l?cosβ,如果动力F的用力方向始终保持竖直向下,当阻力不变时,则杠杆向下运动时的动力变化情况是( )
A.越来越小 B.不变 C.越来越大 D.无法确定
9.(2018,无锡卷)如图,已知点E是矩形ABCD的对角线AC上的一动点,正方形EFGH的顶点G、H都在边AD上,若AB=3,BC=4,则tan∠AFE的值( )
A. 等于 B. 等于 C. 等于 D. 随点E位置的变化而变化
10.(2020,无锡卷)如图,在四边形ABCD中(AB>CD),∠ABC=∠BCD=90°,AB=3,BC =,把Rt△ABC沿着AC翻折得到Rt△AEC,若tan∠AED =,则线段DE的长度是( )
A. B. C. D.
(第8题) (第9题) (第10题)
二、填空题(每题2分,共16分)
11. 在△ABC中,,则∠C =_______°
12. 如图,在半径为3的⊙O中,直径AB与弦CD相交于点E,连接AC,BD,若AC=2,则cos D =________
13. 如图,在△ABC中,∠ACB=90°,点D为AB边的中点,连接CD,若BC=4,CD=3,则cos∠DCB的值为________
(第13题图) (第14题图) (第15题图)
14. 如图所示的网格是正方形网格,∠BAC ______ ∠DAE.(填“>”,“=”或“<”)
15. (2017,无锡卷)在如图的正方形方格纸中,每个小的四边形都是相同的正方形,A,B,C,D都在格点处,AB与CD相交于O,则tan∠BOD的值等于_______.
16. (2019,镇江卷)如图所示,在四边形ABCD中,∠B=90°,AB=2,CD=8.连接AC,AC⊥CD,若sin∠ACB =,则AD长度是_________
(第16题图) (第17题图)
17. 如图,某校教学楼后面紧邻着一个山坡,坡上面是一块平地.BC∥AD,BE⊥AD,斜坡AB长26m,斜坡AB的坡比为12:5.为了减缓坡面,防止山体滑坡,学校决定对该斜坡进行改造.经地质人员勘测,当坡角不超过50°时,可确保山体不滑坡.如果改造时保持坡脚A不动,则坡顶B沿BC至少向右移________m时,才能确保山体不滑坡.
(参考数据:tan50°≈1.2)
18.(2019,宿迁)如图,∠MAN=60°,若△ABC的顶点B在射线AM上,且AB=2,点C在射线AN上运动,当△ABC是锐角三角形时,BC的取值范围是_________
三、计算题(每题8分,共16分)
19. 如图,在Rt△ABC中,∠ACB=90°,AC=BC=3,点D在边AC上,且AD=2CD,DE⊥AB,垂足为点E,连接CE,求:
(1)线段BE的长;
(2)∠ECB的正切值.
20. 已知△ABC中,AB = 10,AC = 2,∠B=30°,求△ABC的面积。
(改编自2018年无锡中考数学卷第17题)
四、解答题(共38分)
21. (本题满分6分)如图,楼房AB建在山坡BC上,其坡度为i =1:2,小明从山坡底部C处测得点A的仰角为56.35°,已知山坡的高度BD为10米,求楼房AB的高.
(结果精确到1米)(注:坡度i是指坡面的铅直高度BD与水平宽度CD的比)
参考数据:sin56.35°≈ 0.83,cos56.35° ≈ 0.55,tan56.35° ≈ 1.50
22. (本题满分6分)如图,要在原始森林附近修一条公路MN,已知C点周围260米范围内为原始森林保护区,在M上的点A处测得C在A的东北方向上(即∠DAC=45°),从A向东走800米到达B处,测得C在点B的北偏西60°方向上,MN是否穿过原始森林保护区,为什么?(结果精确到个位,参考数据:)
23. (本题满分8分)如图,在Rt△ABC中,∠C=90°,AD是△ABC的角平分线,点O在边AB上.过点A、D的圆的圆心O在边AB上,它与边AB交于另一点E.
(1)试判断BC与圆O的位置关系,并说明理由;
(2)若AC = 6,sin B =,求AD的长。
24. (本题满分8分)如图,四边形ABCD内接于⊙O,AB=17,CD=10,∠A=90°,
cos B =,求AD的长.
25. (本题10分)如图,某数学兴趣小组为测量一棵古树BH和教学楼CG的高,先在A处用高2米的测角仪测得古树顶端H的仰角∠HDE为45°,此时教学楼顶端G恰好在视线DH上,再向前走6米到达B处,又测得教学楼顶端G的仰角∠GEF为60°,点A、B、C三点在同一水平线上.
(1)计算古树BH的高;
(2)计算教学楼CG的高.(结果保留根号)
【简明参考答案】
1~10 A B C D B B A A A B
11. 75° 12. 13. 14. >
15. 3 16. 10 17. 10 18.
19.(1)BE = (2)tan∠ECB = 2
20. 15 或 (分类讨论三角形的形状)
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
