2020-2021学年八年级数学下学期华东师大版 16.1 分式及其基本性质(培优卷)(Word版 含答案)
文档属性
| 名称 | 2020-2021学年八年级数学下学期华东师大版 16.1 分式及其基本性质(培优卷)(Word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 307.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-20 00:00:00 | ||
图片预览



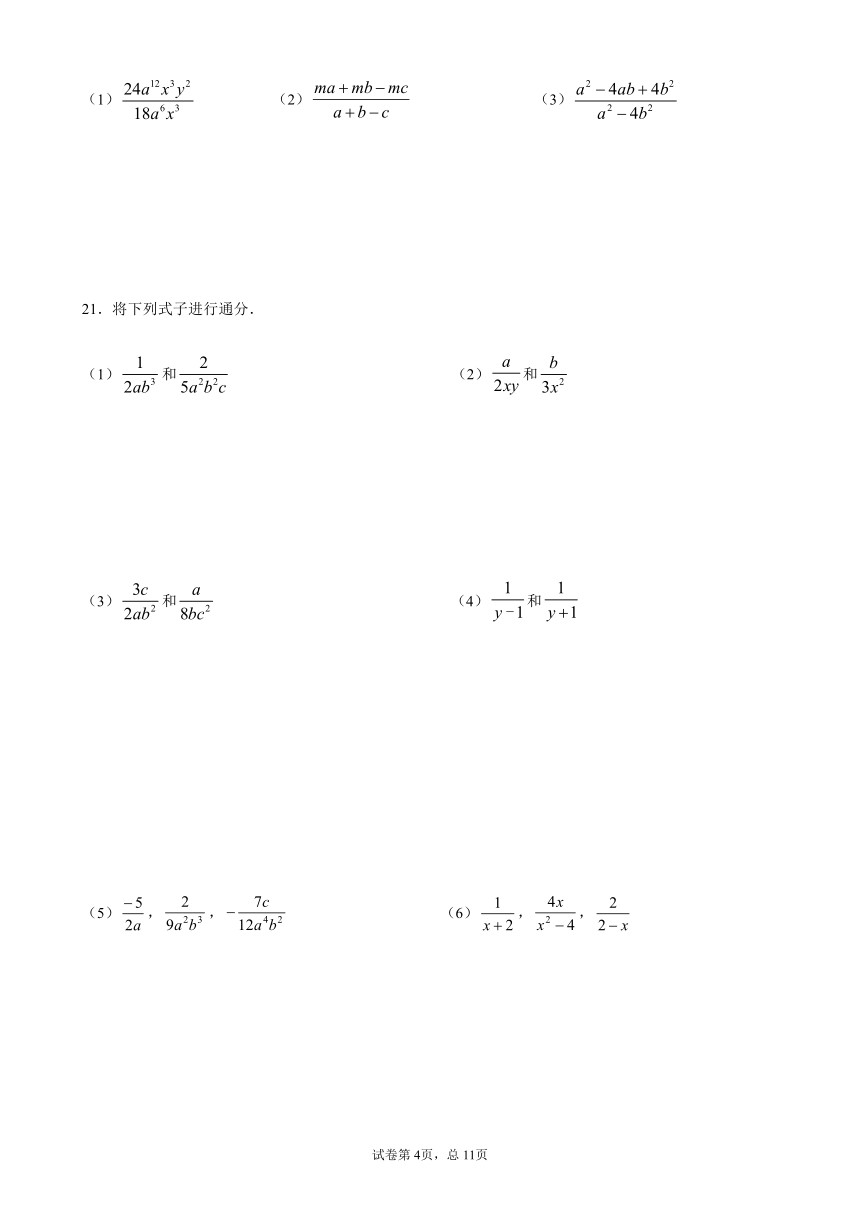
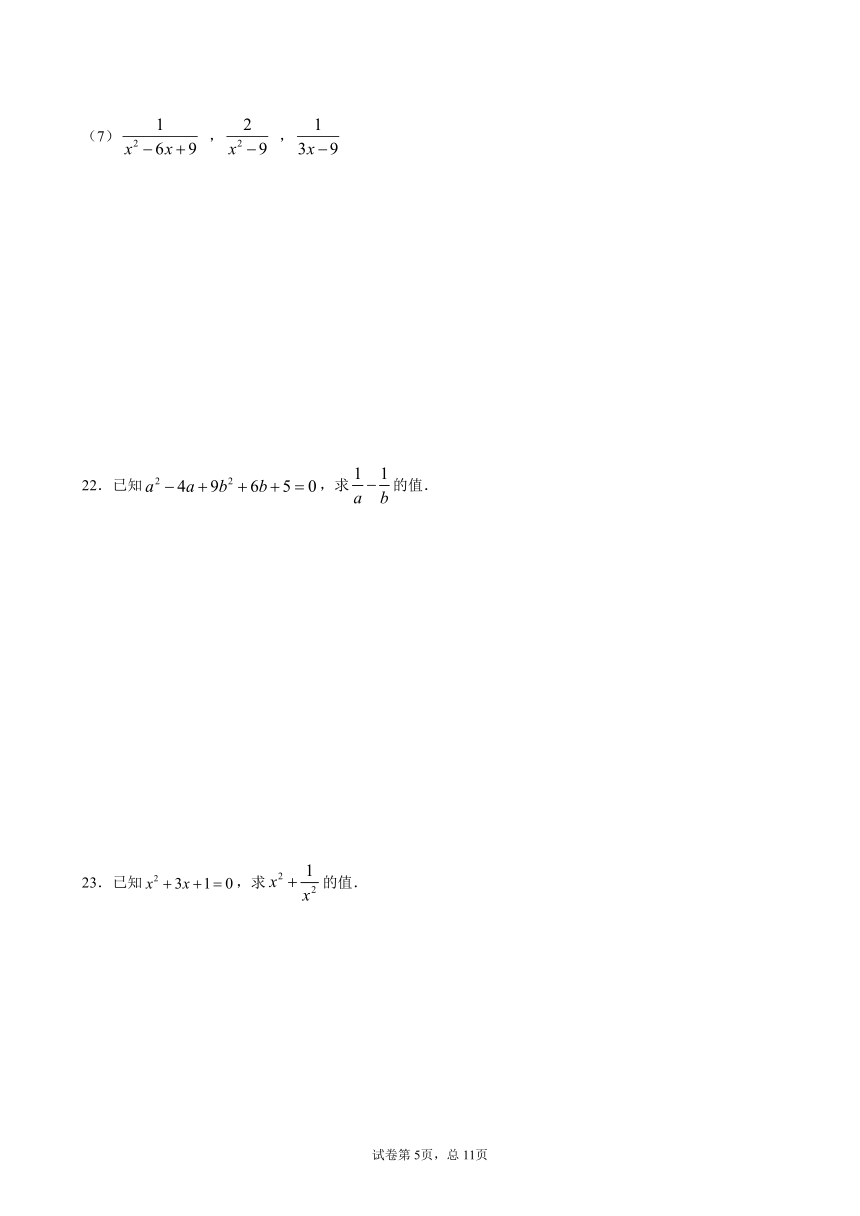
文档简介
16.1
分式及其基本性质(培优卷)
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在代数式,,,中,分式有(
)
A.1个
B.2个
C.3个
D.4个
2.要使分式有意义,则的取值范围是(
)
A.
B.
C.且
D.
3.分式无意义,则的取值范围是(
)
A.
B.
C.
D.一切实数
4.分式,,的最简公分母是(
)
A.
B.
C.
D.
5.关于分式,下列说法不正确的是( )
A.当x=0时,分式没有意义
B.当x>5时,分式的值为正数
C.当x<5时,分式的值为负数
D.当x=5时,分式的值为0
6.下列判断错误的是( )
A.当a≠0时,分式有意义
B.当a=﹣3时,分式有意义
C.当时,分式的值为0
D.当a=1时,分式的值为1
7.当分式的值为0时,则等于(
)
A.3
B.0
C.
D.-3
8.下列分式中,最简分式是(
)
A.
B.
C.
D.
9.已知a2-5ab+6b2=0,则的值是(
)
A.-
B.-
C.或
D.-或-
10.已知,则分式的值为(
)
A.1
B.5
C.
D.
11.使分式的值为负的条件是(
)
A.x<0
B.x>0
C.x>
D.x<
12.若取整数,使分式的值为整数的值有(
)
A.2个
B.4个
C.6个
D.8个
二、填空题
13.将分式的分子、分母各项系数化为整数,其结果为_______________.
14.已知的值为4,若分式中的、均扩大2倍,则的值为__________.
15.在分式,,,中,最简分式有__________个.
16.对于两个非零的实数a,b,定义运算※如下:例如:若,则的值为__________.
17.已知,则__________.
18.已知,,,,...则的值为__________.
三、解答题
19.约分:
(1)
(2)
(3)
(4)
(5)
(6)
.
20.约分
(1)
(2)
(3)
21.将下列式子进行通分.
(1)和
(2)和
(3)和
(4)和
(5),,
(6),,
(7)
,
,
22.已知,求的值.
23.已知,求的值.
24.若分式的值是正数、负数、0时,求的取值范围.
25.例:解不等式(x﹣2)(x+3)>0
解:由实数的运算法则:“两数相乘,同号得正”
得①,或②,
解不等式组①得,x>2,
解不等式组②得,x<﹣3,
所以原不等式的解集为x>2或x<﹣3.
阅读例题,尝试解决下列问题:
(1)平行运用:解不等式x2﹣9>0;
(2)类比运用:若分式的值为负数,求x的取值范围.
26.对于正数x,规定:.
例如:,,.
(1)填空:________;_______;_________;
(2)猜想:_________,并证明你的结论;
(3)求值:.
参考答案
一、选择题
1
2
3
4
5
6
7
8
9
10
11
12
B
B
C
C
C
B
D
B
C
A
C
B
二、填空题
13
14
15
16
17
18
8
2
三、解答题
19.
(1)
=;
(2)=.
(3)原式
(4)原式
.
(5)原式
.
(6)原式
.
20.
解:(1)==
(2)==m
(3)==
21.
解:(1)两式的最简公分母为10a2b3c,
故==
==
(2)两式的最简公分母为6x2y,
故==
==
(3)两式的最简公分母为8ab2c2
故==
==
(4)两式的最简公分母为y2-1
故,
.
最简公分母是36a4b3
∴
最简公分母是(x+2)(x-2)
(7)最简公分母是,
所以
22.
∵
a2﹣4a+9b2+6b+5=0,∴(a﹣2)2+(3b+1)2=0,∴a﹣2=0,3b+1=0,即a=2,b=﹣.
当a=2,b=﹣时,原式=+3=3.
23.
∵
x2+3x+1=0,∴x+3+=0,∴x+=﹣3,∴x2+=(x+)2﹣2=(﹣3)2﹣2=7.
24.
解:当或时,分式的值为正数;
当时,分式的值为负数;
当时,分式的值为0.
25.
(1)解不等式x2﹣9>0,即为解,
根据“两数相乘,同号得正”
得①,或②,
解不等式组①得,x>3,
解不等式组②得,x<﹣3,
∴原不等式的解集为x>3或x<﹣3;
(2)由题得不等式,
根据“两数相除,同号得正,异号得负”
得①,或②,
解不等式组①得,,
不等式组②无解,
∴原不等式的解集为.
26.
解:(1)
=,
=,,+=1,
(2),
理由为:,
,
则.
(3)原式
.
试卷第1页,总3页
试卷第1页,总3页
分式及其基本性质(培优卷)
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在代数式,,,中,分式有(
)
A.1个
B.2个
C.3个
D.4个
2.要使分式有意义,则的取值范围是(
)
A.
B.
C.且
D.
3.分式无意义,则的取值范围是(
)
A.
B.
C.
D.一切实数
4.分式,,的最简公分母是(
)
A.
B.
C.
D.
5.关于分式,下列说法不正确的是( )
A.当x=0时,分式没有意义
B.当x>5时,分式的值为正数
C.当x<5时,分式的值为负数
D.当x=5时,分式的值为0
6.下列判断错误的是( )
A.当a≠0时,分式有意义
B.当a=﹣3时,分式有意义
C.当时,分式的值为0
D.当a=1时,分式的值为1
7.当分式的值为0时,则等于(
)
A.3
B.0
C.
D.-3
8.下列分式中,最简分式是(
)
A.
B.
C.
D.
9.已知a2-5ab+6b2=0,则的值是(
)
A.-
B.-
C.或
D.-或-
10.已知,则分式的值为(
)
A.1
B.5
C.
D.
11.使分式的值为负的条件是(
)
A.x<0
B.x>0
C.x>
D.x<
12.若取整数,使分式的值为整数的值有(
)
A.2个
B.4个
C.6个
D.8个
二、填空题
13.将分式的分子、分母各项系数化为整数,其结果为_______________.
14.已知的值为4,若分式中的、均扩大2倍,则的值为__________.
15.在分式,,,中,最简分式有__________个.
16.对于两个非零的实数a,b,定义运算※如下:例如:若,则的值为__________.
17.已知,则__________.
18.已知,,,,...则的值为__________.
三、解答题
19.约分:
(1)
(2)
(3)
(4)
(5)
(6)
.
20.约分
(1)
(2)
(3)
21.将下列式子进行通分.
(1)和
(2)和
(3)和
(4)和
(5),,
(6),,
(7)
,
,
22.已知,求的值.
23.已知,求的值.
24.若分式的值是正数、负数、0时,求的取值范围.
25.例:解不等式(x﹣2)(x+3)>0
解:由实数的运算法则:“两数相乘,同号得正”
得①,或②,
解不等式组①得,x>2,
解不等式组②得,x<﹣3,
所以原不等式的解集为x>2或x<﹣3.
阅读例题,尝试解决下列问题:
(1)平行运用:解不等式x2﹣9>0;
(2)类比运用:若分式的值为负数,求x的取值范围.
26.对于正数x,规定:.
例如:,,.
(1)填空:________;_______;_________;
(2)猜想:_________,并证明你的结论;
(3)求值:.
参考答案
一、选择题
1
2
3
4
5
6
7
8
9
10
11
12
B
B
C
C
C
B
D
B
C
A
C
B
二、填空题
13
14
15
16
17
18
8
2
三、解答题
19.
(1)
=;
(2)=.
(3)原式
(4)原式
.
(5)原式
.
(6)原式
.
20.
解:(1)==
(2)==m
(3)==
21.
解:(1)两式的最简公分母为10a2b3c,
故==
==
(2)两式的最简公分母为6x2y,
故==
==
(3)两式的最简公分母为8ab2c2
故==
==
(4)两式的最简公分母为y2-1
故,
.
最简公分母是36a4b3
∴
最简公分母是(x+2)(x-2)
(7)最简公分母是,
所以
22.
∵
a2﹣4a+9b2+6b+5=0,∴(a﹣2)2+(3b+1)2=0,∴a﹣2=0,3b+1=0,即a=2,b=﹣.
当a=2,b=﹣时,原式=+3=3.
23.
∵
x2+3x+1=0,∴x+3+=0,∴x+=﹣3,∴x2+=(x+)2﹣2=(﹣3)2﹣2=7.
24.
解:当或时,分式的值为正数;
当时,分式的值为负数;
当时,分式的值为0.
25.
(1)解不等式x2﹣9>0,即为解,
根据“两数相乘,同号得正”
得①,或②,
解不等式组①得,x>3,
解不等式组②得,x<﹣3,
∴原不等式的解集为x>3或x<﹣3;
(2)由题得不等式,
根据“两数相除,同号得正,异号得负”
得①,或②,
解不等式组①得,,
不等式组②无解,
∴原不等式的解集为.
26.
解:(1)
=,
=,,+=1,
(2),
理由为:,
,
则.
(3)原式
.
试卷第1页,总3页
试卷第1页,总3页
