2020-2021学年八年级数学北师大版下册1.1 等腰三角形 同步测试(Word版 含答案)
文档属性
| 名称 | 2020-2021学年八年级数学北师大版下册1.1 等腰三角形 同步测试(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 73.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-20 08:04:08 | ||
图片预览


文档简介
1.1等腰三角形
同步练习
一.选择题
1.等腰三角形中有一个角为100°,则其底角为( )
A.50°
B.40°
C.40°或100°
D.50°或100°
2.下列说法错误的是( )
A.等腰三角形的两个底角相等
B.等腰三角形的高、中线、角平分线互相重合
C.三角形两边的垂直平分线的交点到三个顶点距离相等
D.等腰三角形顶角的外角是其底角的2倍
3.如图,每个小方格的边长为1,A,B两点都在小方格的顶点上,点C也是图中小方格的顶点,并且△ABC是等腰三角形,那么点C的个数为( )
A.1
B.2
C.3
D.4
4.如图,已知OA=OB=OC,BC∥AO,若∠A=36°,则∠B等于( )
A.54°
B.60°
C.72°
D.76°
5.如图,△ABC是等边三角形,点D是AC的中点,DE⊥BC,CE=3,则AB等于( )
A.11
B.12
C.13
D.14
6.如图所示,在等边三角形ABC中,AD⊥BC,E为AD上一点,∠CED=50°,则∠ABE等于( )
A.10°
B.15°
C.20°
D.25°
7.下列条件中,不能判定△ABC是等腰三角形的是( )
A.a=3,b=3,c=4
B.a:b:c=2:3:4
C.∠B=50°,∠C=80°
D.∠A:∠B:∠C=1:1:2
8.如图,△ABC与△DCE都是等边三角形,B,C,E三点在同一条直线上,若AB=3,∠BAD=150°,则DE的长为( )
A.3
B.4
C.5
D.6
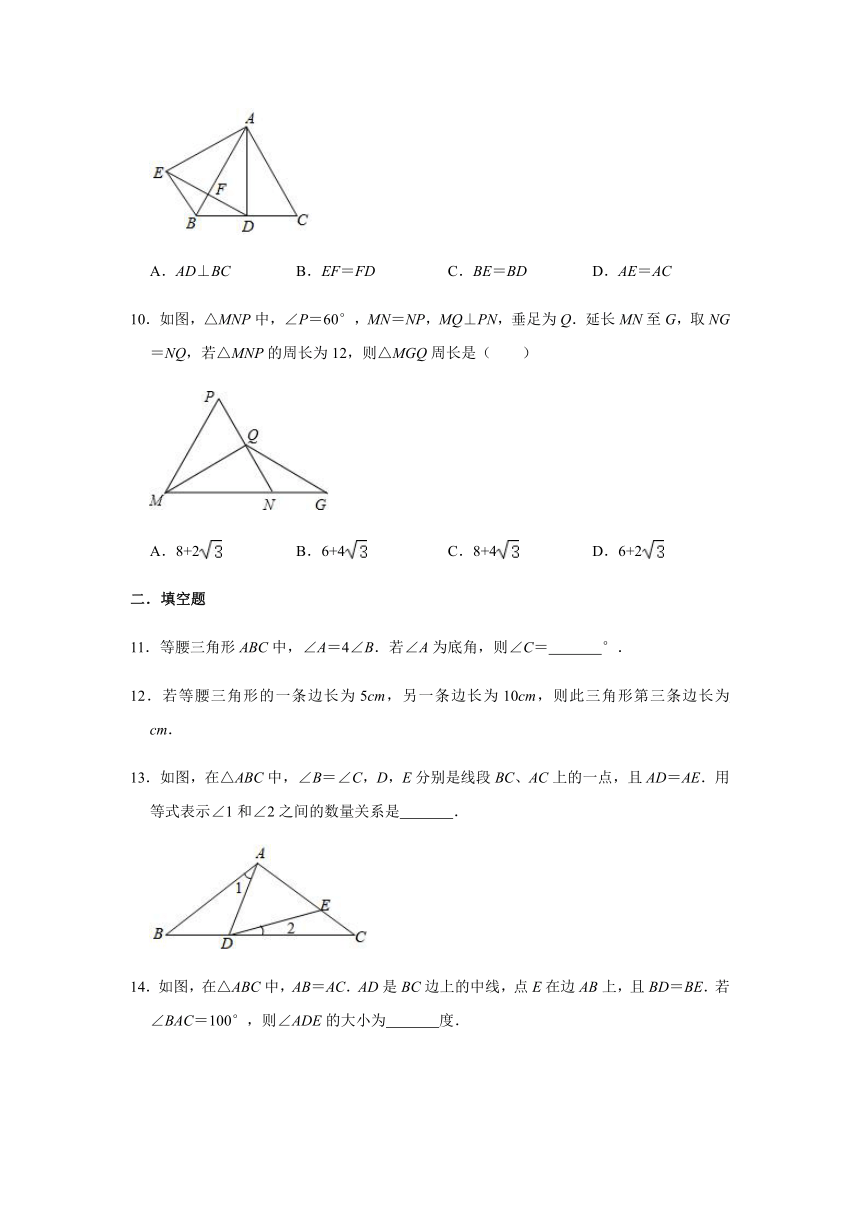
9.如图,△ABC是等边三角形,AD是角平分线,△ADE是等边三角形,下列结论不正确的是( )
A.AD⊥BC
B.EF=FD
C.BE=BD
D.AE=AC
10.如图,△MNP中,∠P=60°,MN=NP,MQ⊥PN,垂足为Q.延长MN至G,取NG=NQ,若△MNP的周长为12,则△MGQ周长是( )
A.8+2
B.6+4
C.8+4
D.6+2
二.填空题
11.等腰三角形ABC中,∠A=4∠B.若∠A为底角,则∠C=
°.
12.若等腰三角形的一条边长为5cm,另一条边长为10cm,则此三角形第三条边长为
cm.
13.如图,在△ABC中,∠B=∠C,D,E分别是线段BC、AC上的一点,且AD=AE.用等式表示∠1和∠2之间的数量关系是
.
14.如图,在△ABC中,AB=AC.AD是BC边上的中线,点E在边AB上,且BD=BE.若∠BAC=100°,则∠ADE的大小为
度.
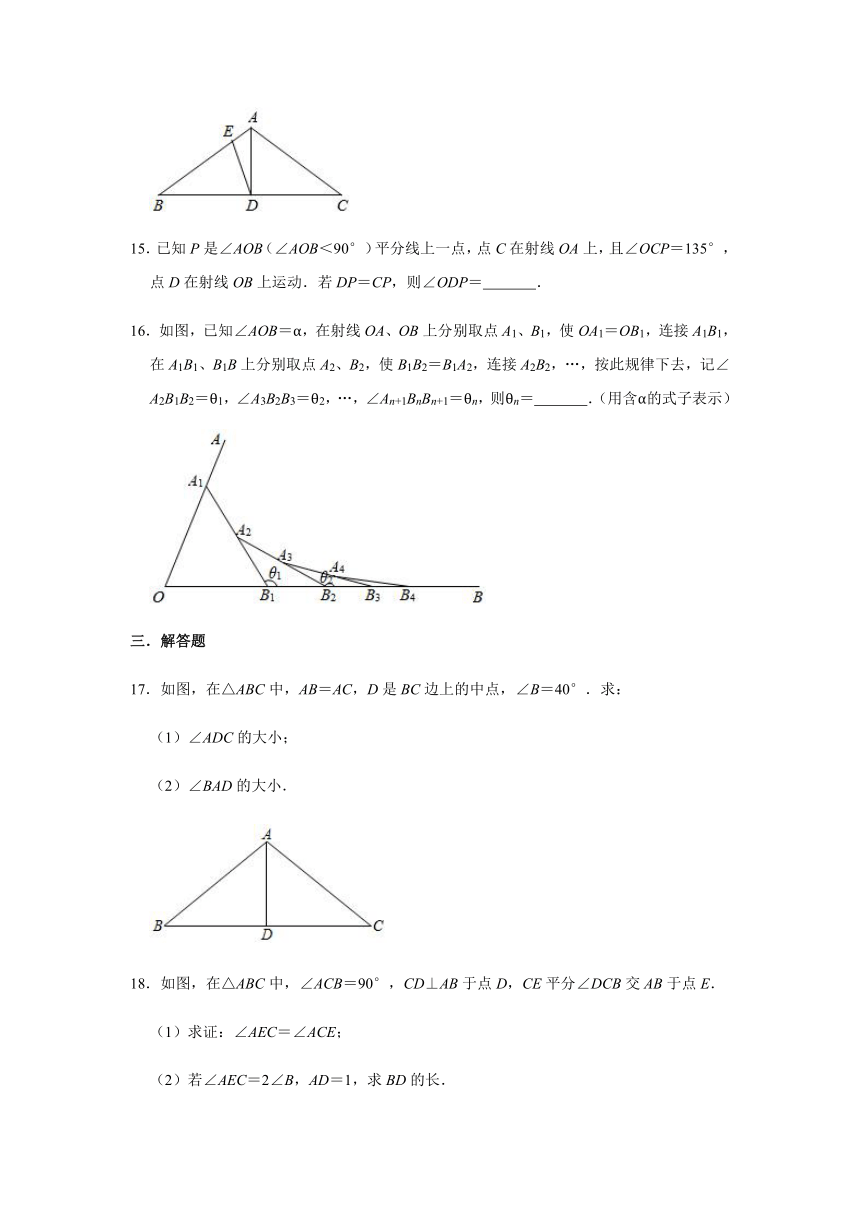
15.已知P是∠AOB(∠AOB<90°)平分线上一点,点C在射线OA上,且∠OCP=135°,点D在射线OB上运动.若DP=CP,则∠ODP=
.
16.如图,已知∠AOB=α,在射线OA、OB上分别取点A1、B1,使OA1=OB1,连接A1B1,在A1B1、B1B上分别取点A2、B2,使B1B2=B1A2,连接A2B2,…,按此规律下去,记∠A2B1B2=θ1,∠A3B2B3=θ2,…,∠An+1BnBn+1=θn,则θn=
.(用含α的式子表示)
三.解答题
17.如图,在△ABC中,AB=AC,D是BC边上的中点,∠B=40°.求:
(1)∠ADC的大小;
(2)∠BAD的大小.
18.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,CE平分∠DCB交AB于点E.
(1)求证:∠AEC=∠ACE;
(2)若∠AEC=2∠B,AD=1,求BD的长.
19.如图所示,已知△ABC中,AB=AC=BC=10厘米,M、N分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度是1厘米/秒的速度,点N的速度是2厘米/秒,当点N第一次到达B点时,M、N同时停止运动.
(1)M、N同时运动几秒后,M、N两点重合?
(2)M、N同时运动几秒后,可得等边三角形△AMN?
(3)M、N在BC边上运动时,能否得到以MN为底边的等腰△AMN,如果存在,请求出此时M、N运动的时间?
参考答案
1.B
2.B
3.C
4.C
5.B
6.C
7.B
8.D
9.D
10.B
11.80
12.10
13.∠1=2∠2
14.
20.
15.135°或45°
16.
17.解:(1)∵AB=AC,D是BC边上的中点,
∴AD⊥BC,即∠ADC=90°;
(2)∵∠B=40°,
∴∠BAD=50°.
18.解:(1)∵∠ACB=90°,CD⊥AB,
∴∠ACD+∠A=∠B+∠A=90°,
∴∠ACD=∠B,
∵CE平分∠BCD,
∴∠BCE=∠DCE,
∴∠B+∠BCE=∠ACD+∠DCE,
即∠AEC=∠ACE;
(2)∵∠AEC=∠B+∠BCE,∠AEC=2∠B,
∴∠B=∠BCE,
又∵∠ACD=∠B,∠BCE=∠DCE,
∴∠ACD=∠BCE=∠DCE,
又∵∠ACB=90°,
∴∠ACD=30°,∠B=30°,
∴Rt△ACD中,AC=2AD=2,
∴Rt△ABC中,AB=2AC=4,
∴BD=AB﹣AD=4﹣1=3.
19.解:(1)设点M、N运动x秒后,M、N两点重合,
x×1+10=2x,
解得:x=10;
(2)设点M、N运动t秒后,可得到等边三角形△AMN,如图①,
AM=t×1=t,AN=AB﹣BN=10﹣2t,
∵三角形△AMN是等边三角形,
∴t=10﹣2t,
解得t=,
∴点M、N运动秒后,可得到等边三角形△AMN.
(3)当点M、N在BC边上运动时,可以得到以MN为底边的等腰三角形,
由(1)知10秒时M、N两点重合,恰好在C处,
如图②,假设△AMN是等腰三角形,
∴AN=AM,
∴∠AMN=∠ANM,
∴∠AMC=∠ANB,
∵AB=BC=AC,
∴△ACB是等边三角形,
∴∠C=∠B,
在△ACM和△ABN中,
∵,
∴△ACM≌△ABN(AAS),
∴CM=BN,
设当点M、N在BC边上运动时,M、N运动的时间y秒时,△AMN是等腰三角形,
∴CM=y﹣10,NB=30﹣2y,CM=NB,
y﹣10=30﹣2y,
解得:y=.故假设成立.
∴当点M、N在BC边上运动时,能得到以MN为底边的等腰△AMN,此时M、N运动的时间为秒.
同步练习
一.选择题
1.等腰三角形中有一个角为100°,则其底角为( )
A.50°
B.40°
C.40°或100°
D.50°或100°
2.下列说法错误的是( )
A.等腰三角形的两个底角相等
B.等腰三角形的高、中线、角平分线互相重合
C.三角形两边的垂直平分线的交点到三个顶点距离相等
D.等腰三角形顶角的外角是其底角的2倍
3.如图,每个小方格的边长为1,A,B两点都在小方格的顶点上,点C也是图中小方格的顶点,并且△ABC是等腰三角形,那么点C的个数为( )
A.1
B.2
C.3
D.4
4.如图,已知OA=OB=OC,BC∥AO,若∠A=36°,则∠B等于( )
A.54°
B.60°
C.72°
D.76°
5.如图,△ABC是等边三角形,点D是AC的中点,DE⊥BC,CE=3,则AB等于( )
A.11
B.12
C.13
D.14
6.如图所示,在等边三角形ABC中,AD⊥BC,E为AD上一点,∠CED=50°,则∠ABE等于( )
A.10°
B.15°
C.20°
D.25°
7.下列条件中,不能判定△ABC是等腰三角形的是( )
A.a=3,b=3,c=4
B.a:b:c=2:3:4
C.∠B=50°,∠C=80°
D.∠A:∠B:∠C=1:1:2
8.如图,△ABC与△DCE都是等边三角形,B,C,E三点在同一条直线上,若AB=3,∠BAD=150°,则DE的长为( )
A.3
B.4
C.5
D.6
9.如图,△ABC是等边三角形,AD是角平分线,△ADE是等边三角形,下列结论不正确的是( )
A.AD⊥BC
B.EF=FD
C.BE=BD
D.AE=AC
10.如图,△MNP中,∠P=60°,MN=NP,MQ⊥PN,垂足为Q.延长MN至G,取NG=NQ,若△MNP的周长为12,则△MGQ周长是( )
A.8+2
B.6+4
C.8+4
D.6+2
二.填空题
11.等腰三角形ABC中,∠A=4∠B.若∠A为底角,则∠C=
°.
12.若等腰三角形的一条边长为5cm,另一条边长为10cm,则此三角形第三条边长为
cm.
13.如图,在△ABC中,∠B=∠C,D,E分别是线段BC、AC上的一点,且AD=AE.用等式表示∠1和∠2之间的数量关系是
.
14.如图,在△ABC中,AB=AC.AD是BC边上的中线,点E在边AB上,且BD=BE.若∠BAC=100°,则∠ADE的大小为
度.
15.已知P是∠AOB(∠AOB<90°)平分线上一点,点C在射线OA上,且∠OCP=135°,点D在射线OB上运动.若DP=CP,则∠ODP=
.
16.如图,已知∠AOB=α,在射线OA、OB上分别取点A1、B1,使OA1=OB1,连接A1B1,在A1B1、B1B上分别取点A2、B2,使B1B2=B1A2,连接A2B2,…,按此规律下去,记∠A2B1B2=θ1,∠A3B2B3=θ2,…,∠An+1BnBn+1=θn,则θn=
.(用含α的式子表示)
三.解答题
17.如图,在△ABC中,AB=AC,D是BC边上的中点,∠B=40°.求:
(1)∠ADC的大小;
(2)∠BAD的大小.
18.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,CE平分∠DCB交AB于点E.
(1)求证:∠AEC=∠ACE;
(2)若∠AEC=2∠B,AD=1,求BD的长.
19.如图所示,已知△ABC中,AB=AC=BC=10厘米,M、N分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度是1厘米/秒的速度,点N的速度是2厘米/秒,当点N第一次到达B点时,M、N同时停止运动.
(1)M、N同时运动几秒后,M、N两点重合?
(2)M、N同时运动几秒后,可得等边三角形△AMN?
(3)M、N在BC边上运动时,能否得到以MN为底边的等腰△AMN,如果存在,请求出此时M、N运动的时间?
参考答案
1.B
2.B
3.C
4.C
5.B
6.C
7.B
8.D
9.D
10.B
11.80
12.10
13.∠1=2∠2
14.
20.
15.135°或45°
16.
17.解:(1)∵AB=AC,D是BC边上的中点,
∴AD⊥BC,即∠ADC=90°;
(2)∵∠B=40°,
∴∠BAD=50°.
18.解:(1)∵∠ACB=90°,CD⊥AB,
∴∠ACD+∠A=∠B+∠A=90°,
∴∠ACD=∠B,
∵CE平分∠BCD,
∴∠BCE=∠DCE,
∴∠B+∠BCE=∠ACD+∠DCE,
即∠AEC=∠ACE;
(2)∵∠AEC=∠B+∠BCE,∠AEC=2∠B,
∴∠B=∠BCE,
又∵∠ACD=∠B,∠BCE=∠DCE,
∴∠ACD=∠BCE=∠DCE,
又∵∠ACB=90°,
∴∠ACD=30°,∠B=30°,
∴Rt△ACD中,AC=2AD=2,
∴Rt△ABC中,AB=2AC=4,
∴BD=AB﹣AD=4﹣1=3.
19.解:(1)设点M、N运动x秒后,M、N两点重合,
x×1+10=2x,
解得:x=10;
(2)设点M、N运动t秒后,可得到等边三角形△AMN,如图①,
AM=t×1=t,AN=AB﹣BN=10﹣2t,
∵三角形△AMN是等边三角形,
∴t=10﹣2t,
解得t=,
∴点M、N运动秒后,可得到等边三角形△AMN.
(3)当点M、N在BC边上运动时,可以得到以MN为底边的等腰三角形,
由(1)知10秒时M、N两点重合,恰好在C处,
如图②,假设△AMN是等腰三角形,
∴AN=AM,
∴∠AMN=∠ANM,
∴∠AMC=∠ANB,
∵AB=BC=AC,
∴△ACB是等边三角形,
∴∠C=∠B,
在△ACM和△ABN中,
∵,
∴△ACM≌△ABN(AAS),
∴CM=BN,
设当点M、N在BC边上运动时,M、N运动的时间y秒时,△AMN是等腰三角形,
∴CM=y﹣10,NB=30﹣2y,CM=NB,
y﹣10=30﹣2y,
解得:y=.故假设成立.
∴当点M、N在BC边上运动时,能得到以MN为底边的等腰△AMN,此时M、N运动的时间为秒.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
