黑龙江省哈尔滨市部分学校2020——2021学年九年级上学期期中数学试卷(五四学制)(Word版 含解析)
文档属性
| 名称 | 黑龙江省哈尔滨市部分学校2020——2021学年九年级上学期期中数学试卷(五四学制)(Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 452.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-20 00:00:00 | ||
图片预览




文档简介
2020-2021学年黑龙江省哈尔滨市部分学校九年级(上)期中数学试卷(五四学制)
一、选择题(每题3分,共计30分)
1.﹣3的倒数是( )
A. B.﹣ C.3 D.﹣3
2.下列运算正确的是( )
A.6a﹣5a=1 B.(a2)3=a5
C.3a2+2a3=5a5 D.a6?a2=a8
3.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
4.下列几何体各自的三视图中,只有两个视图相同的是( )
A.①③ B.②③ C.③④ D.②④
5.将抛物线y=x2向右平移3个单位长度,再向上平移2个单位长度,得到的抛物线的函数表达式为( )
A.y=(x+3)2﹣2 B.y=(x﹣3)2+2 C.y=(x+3)2+2 D.y=(x﹣3)2﹣2
6.如图,在地面上的点A处测得树顶B的仰角为α,AC=2,则树高BC为( )(用含α的代数式表示)
A.2sinα B.2tanα C.2cosα D.
7.如图,BM为⊙O的切线,点B为切点,点A、C在⊙O上,连接AB、AC、BC,若∠MBA=130°,则∠ACB的度数为( )
A.40° B.50° C.60° D.70°
8.抛物线y=x2+2x+1的对称轴是( )
A.直线x=1 B.直线x=﹣1 C.直线y=1 D.直线y=﹣1
9.某商品经过连续两次降价,售价由原来的每件25元降到每件16元,则平均每次降价的百分率为( )
A.20% B.40% C.18% D.36%
10.如图,四边形ABCD是平行四边形,点E在BA的延长线上,点F在BC的延长线上,连接EF,分别交AD,CD于点G,H,则下列结论错误的是( )
A.= B.= C.= D.=
二、填空题(每小题3分,共计30分)
11.将20300000用科学记数法表示为 .
12.在函数y=中,自变量x的取值范围是 .
13.计算2+的结果为 .
14.不等式组的解集是 .
15.反比例函数的图象在每个象限内,y随x的增大而增大,则a的值可以是 .(写出一个符合条件的实数即可)
16.一个扇形的圆心角是120°.它的半径是3cm.则扇形的弧长为 cm.
17.汽车刹车后行驶的距离s米与行驶的时间t秒的函数关系式是s=30t﹣6t2,汽车刹车后到停下来前进了 米.
18.如图,在平面直角坐标中,点O为坐标原点,直线y=kx﹣2k(k<0)交x轴的正半轴于点A,交y轴的正半轴于点B,若BC平分∠ABO交OA于点C,AC=2OC,则k的值为 .
19.如图,在矩形ABCD中,AB=6,BC=8,E、F分别是AD、BC的中点,G是对角线AC上的点,∠EGF=90°,则AG的长为 .
20.如图,△ABC中,CA=CB,点E在BC边上,点D在AC边上,连接AE、DE,若AB=AE,2∠AEB+∠ADE=180°,BE=8,CD=,则CE= .
三、解答题(21、22题每题7分,23、24题每题8分,25、26、27题每题10分)
21.先化简,再求值:(1﹣)÷,其中x=3tan30°+2cos60°.
22.如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点三角形ABC(顶点是网格线的交点).
(1)先将△ABC竖直向上平移6个单位,再水平向右平移3个单位得到△A1B1C1,点A、B、C对应点分别是A1、B1、C1,请画出△A1B1C1;
(2)将△A1B1C1绕B1点顺时针旋转90°,得△A2B1C2,点A1、C1对应点分别是A2、C2,请画出△A2B1C2;
(3)连接CA2,直接写出CA2的长 .
23.某社区为了调查居民对“物业管理”的满意度,随机抽取了部分居民作问卷调查:用“A”表示“相当满意”,“B”表示“满意”,“C”表示“比较满意”,“D”表示“不满意”,下图是工作人员根据问卷调查统计资料绘制的两幅不完整的统计图,请你根据统计图提供的信息解答以下问题:
(1)本次问卷调查,共调查了多少人.
(2)将图(2)中“B”部分的图形补充完整.
(3)如果该社区有居民2000人,请你估计该社区居民对“物业管理”感到“不满意”的约有多少人?
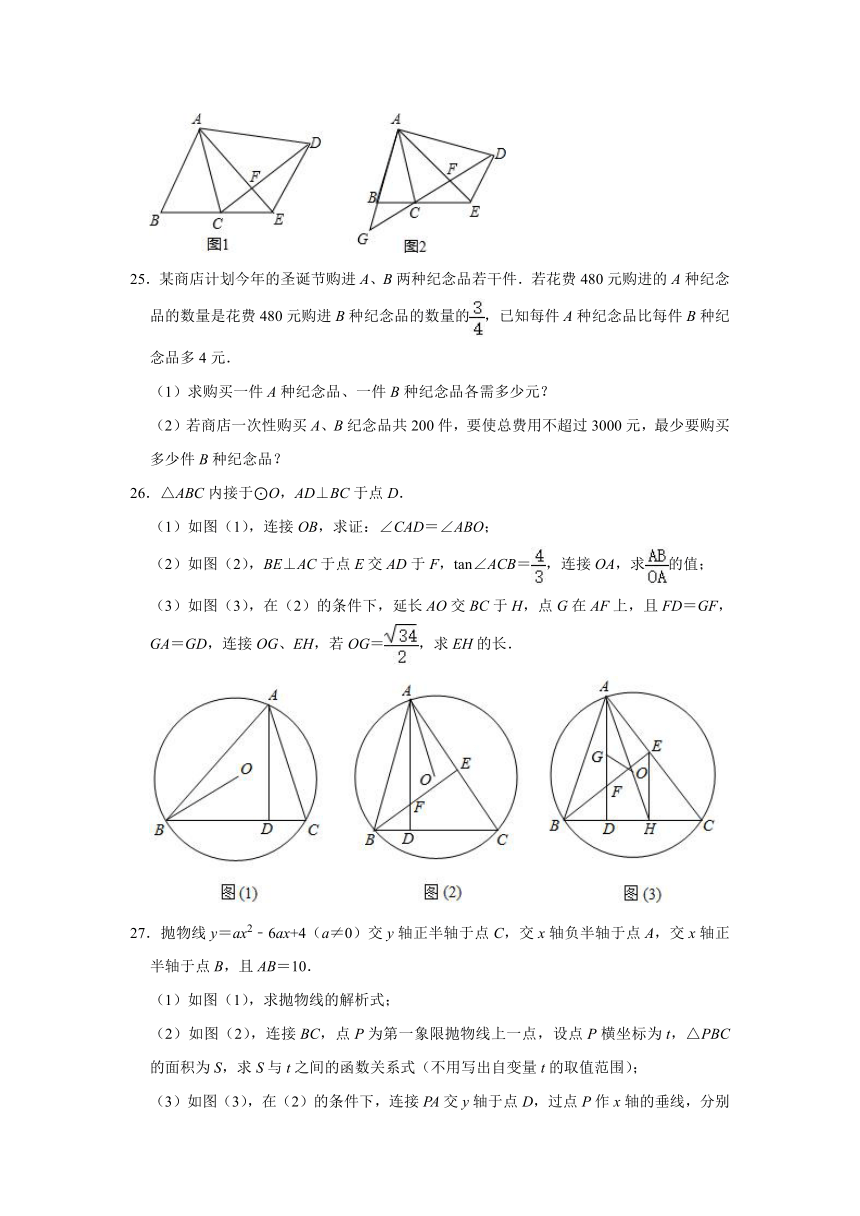
24.如图1,在△ABC和△ADE中,∠BAC=∠EAD,AB=AC,AD=AE,连接CD、AE交于点F.
(1)求证:∠DCE=∠BAC;
(2)当∠BAC=∠EAD=30°,AD⊥AB时(如图2),延长DC、AB交于点G,请直接写出图中除△ABC、△ADE以外的等腰三角形.
25.某商店计划今年的圣诞节购进A、B两种纪念品若干件.若花费480元购进的A种纪念品的数量是花费480元购进B种纪念品的数量的,已知每件A种纪念品比每件B种纪念品多4元.
(1)求购买一件A种纪念品、一件B种纪念品各需多少元?
(2)若商店一次性购买A、B纪念品共200件,要使总费用不超过3000元,最少要购买多少件B种纪念品?
26.△ABC内接于⊙O,AD⊥BC于点D.
(1)如图(1),连接OB,求证:∠CAD=∠ABO;
(2)如图(2),BE⊥AC于点E交AD于F,tan∠ACB=,连接OA,求的值;
(3)如图(3),在(2)的条件下,延长AO交BC于H,点G在AF上,且FD=GF,GA=GD,连接OG、EH,若OG=,求EH的长.
27.抛物线y=ax2﹣6ax+4(a≠0)交y轴正半轴于点C,交x轴负半轴于点A,交x轴正半轴于点B,且AB=10.
(1)如图(1),求抛物线的解析式;
(2)如图(2),连接BC,点P为第一象限抛物线上一点,设点P横坐标为t,△PBC的面积为S,求S与t之间的函数关系式(不用写出自变量t的取值范围);
(3)如图(3),在(2)的条件下,连接PA交y轴于点D,过点P作x轴的垂线,分别交x轴于点E,交BC于点F,连接DF,当∠APE+∠CFD=90°时,在抛物线上是否存在点Q,使得点Q、PE的中点N、点C、是构成以CN为斜边的等腰直角三角形,若存在,请求出点Q的坐标,若不存在,请说明理由.
2020-2021学年黑龙江省哈尔滨市部分学校九年级(上)期中数学试卷(五四学制)
参考答案与试题解析
一.选择题(共10小题)
1.﹣3的倒数是( )
A. B.﹣ C.3 D.﹣3
【分析】根据倒数的概念:乘积是1的两数互为倒数可得答案.
【解答】解:﹣3的倒数是﹣,
故选:B.
2.下列运算正确的是( )
A.6a﹣5a=1 B.(a2)3=a5
C.3a2+2a3=5a5 D.a6?a2=a8
【分析】结合幂的乘方与积的乘方的概念和运算法则进行求解即可.
【解答】解:A、6a﹣5a=a≠1,本选项错误;
B、(a2)3=a6≠a5,本选项错误;
C、3a2+2a3≠5a5,本选项错误;
D、a6?a2=a8,本选项正确.
故选:D.
3.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
【分析】根据轴对称图形与中心对称图形的概念求解.
【解答】解:A、是轴对称图形,也是中心对称图形,故此选项正确;
B、不是轴对称图形,也不是中心对称图形,故此选项错误;
C、是轴对称图形,不是中心对称图形,故此选项错误;
D、不是轴对称图形,是中心对称图形,故此选项错误;
故选:A.
4.下列几何体各自的三视图中,只有两个视图相同的是( )
A.①③ B.②③ C.③④ D.②④
【分析】分别分析四个几何体的三视图,从中找出只有两个视图相同的几何体,可得出结论.
【解答】解:①正方形的主、左和俯视图都是正方形;
②圆锥的主、左视图是三角形,俯视图是显示圆心的圆;
③球体的主、左和俯视图都是圆形;
④圆柱的主、左视图是长方形,俯视图是圆;
只有两个视图相同的几何体是圆锥和圆柱体.
故选:D.
5.将抛物线y=x2向右平移3个单位长度,再向上平移2个单位长度,得到的抛物线的函数表达式为( )
A.y=(x+3)2﹣2 B.y=(x﹣3)2+2 C.y=(x+3)2+2 D.y=(x﹣3)2﹣2
【分析】根据二次函数变化规律:左加右减,上加下减,进而得出变化后解析式.
【解答】解:∵抛物线y=x2向右平移3个单位长度,再向上平移2个单位长度,
∴平移后的解析式为:y=(x﹣3)2+2.
故选:B.
6.如图,在地面上的点A处测得树顶B的仰角为α,AC=2,则树高BC为( )(用含α的代数式表示)
A.2sinα B.2tanα C.2cosα D.
【分析】根据题意可知BC⊥AC,在Rt△ABC中,AC=7米,∠BAC=α,利用锐角三角函数的定义即可求出BC的高度.
【解答】解:∵BC⊥AC,AC=2,∠BAC=α,
∴tanα=,
∴BC=AC?tanα=2tanα,
故选:B.
7.如图,BM为⊙O的切线,点B为切点,点A、C在⊙O上,连接AB、AC、BC,若∠MBA=130°,则∠ACB的度数为( )
A.40° B.50° C.60° D.70°
【分析】直接利用切线的性质得出∠OBM=90°,求出∠AOB的度数,进而利用圆周角定理可得出答案.
【解答】解:如图,连接OA,OB,
∵BM为⊙O的切线,
∴∠OBM=90°,
∵∠MBA=130°,
∴∠ABO=40°,
∵OA=OB,
∴∠BAO=∠ABO=40°,
∴∠AOB=180°﹣40°﹣40°=100°,
∴∠ACB=∠AOB=50°,
故选:B.
8.抛物线y=x2+2x+1的对称轴是( )
A.直线x=1 B.直线x=﹣1 C.直线y=1 D.直线y=﹣1
【分析】由对称轴公式﹣可得对称轴.
【解答】解:∵对称轴x=﹣=﹣=﹣1,
∴对称轴是直线x=﹣1.
故选:B.
9.某商品经过连续两次降价,售价由原来的每件25元降到每件16元,则平均每次降价的百分率为( )
A.20% B.40% C.18% D.36%
【分析】设降价的百分率为x,根据降低率的公式a(1﹣x)2=b建立方程,求解即可.
【解答】解:设降价的百分率为x
根据题意可列方程为25(1﹣x)2=16
解方程得,(舍)
∴每次降价的百分率为20%
故选:A.
10.如图,四边形ABCD是平行四边形,点E在BA的延长线上,点F在BC的延长线上,连接EF,分别交AD,CD于点G,H,则下列结论错误的是( )
A.= B.= C.= D.=
【分析】根据相似三角形的判定和性质进行判断即可.
【解答】解:∵四边形ABCD是平行四边形,
∴AD∥BF,BE∥DC,AD=BC,
∴,,,
故选:C.
二.填空题
11.将20300000用科学记数法表示为 2.03×107 .
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数;当原数的绝对值<1时,n是负整数.
【解答】解:数字20300000科学记数法可表示为2.03×107.
故答案为:2.03×107.
12.在函数y=中,自变量x的取值范围是 x≠2 .
【分析】根据函数表达式是整式时,自变量可取全体实数解答.
【解答】解:当x﹣2≠0,即x≠2时,函数y=有意义.
故答案为:全x≠2.
13.计算2+的结果为 3 .
【分析】首先化简二次根式,进而合并求出答案.
【解答】解:原式=2×+2=3.
故答案为:3.
14.不等式组的解集是 x≤2 .
【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
【解答】解:解不等式6﹣3x≥0,得:x≤2,
解不等式2x<x+4,得:x<4,
则不等式组的解集为x≤2,
故答案为x≤2.
15.反比例函数的图象在每个象限内,y随x的增大而增大,则a的值可以是 ﹣4 .(写出一个符合条件的实数即可)
【分析】根据反比例函数的性质解答.
【解答】解:依题意有a+3<0,则a<﹣3.故a的值可以是﹣4.(答案不唯一,符合条件的实数即可.)
16.一个扇形的圆心角是120°.它的半径是3cm.则扇形的弧长为 2π cm.
【分析】根据弧长公式可得结论.
【解答】解:根据题意,扇形的弧长为=2π,
故答案为:2π
17.汽车刹车后行驶的距离s米与行驶的时间t秒的函数关系式是s=30t﹣6t2,汽车刹车后到停下来前进了 米.
【分析】利用配方法求二次函数最值的方法解答即可.
【解答】解:∵s=30t﹣6t2=﹣6(t﹣)2+,
∴汽车刹车后到停下来前进了m.
故答案为:.
18.如图,在平面直角坐标中,点O为坐标原点,直线y=kx﹣2k(k<0)交x轴的正半轴于点A,交y轴的正半轴于点B,若BC平分∠ABO交OA于点C,AC=2OC,则k的值为 ﹣ .
【分析】过点C作CD⊥AB于点D,则OC=CD,利用面积法结合AB=2OC,可得出AB=2OA,利用勾股定理可得出OA=OB,利用一次函数图象上点的坐标特征可求出OA,OB的长,结合OA=OB可求出k值.
【解答】解:过点C作CD⊥AB于点D,则OC=CD,如图所示.
∵S△BOC=OC?OB,S△ABC=AC?OB=AB?CD,
∴===2,
∴AB=2OB,
∴OA==OB.
当x=0时,直线y=kx﹣2k=﹣2k,
∴OB=﹣2k;
当y=0时,y=kx﹣2k=0,解得:x=2,
∴OA=2,
∴2=×(﹣2k),
∴k=﹣.
故答案为:﹣.
19.如图,在矩形ABCD中,AB=6,BC=8,E、F分别是AD、BC的中点,G是对角线AC上的点,∠EGF=90°,则AG的长为 2或8 .
【分析】连接EF交AC于O,先证四边形ABFE是矩形,得EF=AB=6,EF∥AB,再证OF是△ABC的中位线,得OA=OC=AC=5,然后由直角三角形的性质得OG=EF=3,分两种情况求出即可.
【解答】解:如图,连接EF交AC于点O,
∵四边形ABCD是矩形,
∴∠B=∠BAD=90°,AD=BC=8,AD∥BC,
∴AC===10,
∵E、F分别是AD、BC的中点,
∴AE=BF=4,AE∥BF,
∴四边形ABFE是平行四边形,
∵∠BAE=90°,
∴四边形ABFE是矩形,
∴EF=AB=6,EF∥AB,
∴OF是△ABC的中位线,
∴OA=OC=AC=5,
∵∠EGF=90°,
∴OG=EF=3,
当点G在线段OA上时,AG=OA﹣OG=2,
当点G在线段OC上时,AG′=OA+OG'=8;
故答案为:2或8.
20.如图,△ABC中,CA=CB,点E在BC边上,点D在AC边上,连接AE、DE,若AB=AE,2∠AEB+∠ADE=180°,BE=8,CD=,则CE= 12 .
【分析】过点A作AM⊥BE于E,过点D作DN⊥EC于N,由等腰三角形的性质和三角形内角和定理可求∠C=∠DEC,可得DE=DC=,通过证明△CDN∽△CAM,可得,即可求解.
【解答】解:如图,过点A作AM⊥BE于E,过点D作DN⊥EC于N,
∵CA=CB,AB=AE,
∴∠B=∠CAB,∠B=∠AEB,
∴∠B=∠CAB=∠AEB,
∵∠B+∠BAC+∠C=180°,∠B+∠AEB+∠BAE=180°,
∴∠C=∠BAE,
∴2∠AEB+∠C=180°,
又∵2∠AEB+∠ADE=180°,
∴∠C=∠ADE,
又∵∠ADE=∠C+∠DEC,
∴∠C=∠DEC,
∴DE=DC=,
∵AB=AE,AM⊥BE,DE=CC,DN⊥EC,
∴BM=ME=BE=4,EN=NC=EC,AM∥DN,
∴△CDN∽△CAM,
∴,
∴,
∴EC=12,EC=﹣5(不合题意舍去),
故答案为:12.
三.解答题(共7小题)
21.先化简,再求值:(1﹣)÷,其中x=3tan30°+2cos60°.
【分析】先根据分式混合运算的法则把原式进行化简,再求出x的值代入进行计算即可.
【解答】解:原式=?
=,
∵x=3×+2×=+1,
∴原式===.
22.如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点三角形ABC(顶点是网格线的交点).
(1)先将△ABC竖直向上平移6个单位,再水平向右平移3个单位得到△A1B1C1,点A、B、C对应点分别是A1、B1、C1,请画出△A1B1C1;
(2)将△A1B1C1绕B1点顺时针旋转90°,得△A2B1C2,点A1、C1对应点分别是A2、C2,请画出△A2B1C2;
(3)连接CA2,直接写出CA2的长 .
【分析】(1)将点A、B、C分别向上平移6个单位、向右平移3个单位得到平移后的对应点,再首尾顺次连接即可;
(2)将点A1、C1分别绕B1点顺时针旋转90得到对应点,再与点B1首尾顺次连接即可;
(3)利用勾股定理求解即可.
【解答】解:(1)如图所示,△A1B1C1即为所求.
(2)如图所示,△A2B1C2即为所求.
(3)CA2==,
故答案为:.
23.某社区为了调查居民对“物业管理”的满意度,随机抽取了部分居民作问卷调查:用“A”表示“相当满意”,“B”表示“满意”,“C”表示“比较满意”,“D”表示“不满意”,下图是工作人员根据问卷调查统计资料绘制的两幅不完整的统计图,请你根据统计图提供的信息解答以下问题:
(1)本次问卷调查,共调查了多少人.
(2)将图(2)中“B”部分的图形补充完整.
(3)如果该社区有居民2000人,请你估计该社区居民对“物业管理”感到“不满意”的约有多少人?
【分析】(1)根据条形图可得C人数为100人,根据扇形图可得C占总人数的20%,再用100除以20%可得答案;
(2)首先利用总数减去各条的纵坐标可得答案;
(3)利用样本估计总体的方法用2000乘以感到“不满意”的人数所占百分比.
【解答】解:(1)100÷20%=500(人),
本次问卷调查,共调查了500人.
(2)500﹣200﹣100﹣50=150(人),
如图.
(3)如果该校有学生2000人,则该校学生对教学感到“不满意”的约有:2000×10%=200(人).
24.如图1,在△ABC和△ADE中,∠BAC=∠EAD,AB=AC,AD=AE,连接CD、AE交于点F.
(1)求证:∠DCE=∠BAC;
(2)当∠BAC=∠EAD=30°,AD⊥AB时(如图2),延长DC、AB交于点G,请直接写出图中除△ABC、△ADE以外的等腰三角形.
【分析】(1)如图1,先证明△ACD≌△ABE,得∠ACD=∠ABC,根据三角形内角和与平角定义得出结论;
(2)如图2,图形中有四个等腰三角形:分别是①△ACF是等腰三角形,②△ADG是等腰直角三角形,③△DEF是等腰三角形;④△ECD是等腰三角形;根据已知角的度数依次计算各角的度数,根据两个角相等的三角形是等腰三角形得出结论.
【解答】证明:(1)如图1,∵∠BAC=∠EAD,
∴∠BAC+∠CAE=∠EAD+∠CAE,
即∠BAE=∠CAD,
∵AB=AC,AD=AE,
∴△ACD≌△ABE,
∴∠ACD=∠ABC,
∵∠BAC+∠ABC+∠ACB=180°,
∠ECD+∠ACD+∠ACB=180°,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠BAC+2∠ACB=180°,
∠ECD+2∠ACB=180°,
∴∠BAC=∠ECD;
(2)如图2,
①∵∠BAC=∠EAD=30°,
∴∠ABC=∠ACB=∠AED=∠ADE=75°,
由(1)得:∠ACD=∠ABC=75°,
∠DCE=∠BAC=30°,
∵AD⊥AB,
∴∠BAD=90°,
∴∠CAE=30°,
∴∠AFC=180°﹣30°﹣75°=75°,
∴∠ACF=∠AFC,
∴△ACF是等腰三角形,
②∵∠BCG=∠DCE=30°,∠ABC=75°,
∴∠G=45°,
在Rt△AGD中,∠ADG=45°,
∴△ADG是等腰直角三角形,
③∠EDF=75°﹣45°=30°,
∴∠DEF=∠DFE=75°,
∴△DEF是等腰三角形;
④∵∠ECD=∠EDC=30°,
∴△ECD是等腰三角形.
25.某商店计划今年的圣诞节购进A、B两种纪念品若干件.若花费480元购进的A种纪念品的数量是花费480元购进B种纪念品的数量的,已知每件A种纪念品比每件B种纪念品多4元.
(1)求购买一件A种纪念品、一件B种纪念品各需多少元?
(2)若商店一次性购买A、B纪念品共200件,要使总费用不超过3000元,最少要购买多少件B种纪念品?
【分析】(1)设购买一件B种纪念品需x元,则购买一件A种纪念品需(x+4)元,根据数量=总价÷单价结合花费480元购进的A种纪念品的数量是花费480元购进B种纪念品的数量的,即可得出关于x的分式方程,解之经检验后即可得出结论;
(2)设购买m件B种纪念品,则购买(200﹣m)件A种纪念品,根据总价=单价×数量结合要使总费用不超过3000元,即可得出关于m的一元一次不等式,解之取其中的最小值即可得出结论.
【解答】解:(1)设购买一件B种纪念品需x元,则购买一件A种纪念品需(x+4)元,
依题意,得:=×,
解得:x=12,
经检验,x=12是原方程的解,且符合题意,
∴x+4=16.
答:购买一件A种纪念品需16元,购买一件B种纪念品需12元.
(2)设购买m件B种纪念品,则购买(200﹣m)件A种纪念品,
依题意,得:16(200﹣m)+12m≤3000,
解得:m≥50.
答:最少要购买50件B种纪念品.
26.△ABC内接于⊙O,AD⊥BC于点D.
(1)如图(1),连接OB,求证:∠CAD=∠ABO;
(2)如图(2),BE⊥AC于点E交AD于F,tan∠ACB=,连接OA,求的值;
(3)如图(3),在(2)的条件下,延长AO交BC于H,点G在AF上,且FD=GF,GA=GD,连接OG、EH,若OG=,求EH的长.
【分析】(1)如图,延长BO交⊙O于E,连接AE.利用等角的余角相等解决问题即可.
(2)如图(2)中,过点O作OT⊥AC于T.证明△ADB∽△ATO,可得=,解决问题.
(3)如图3中,作OR⊥AD于R,延长AD交⊙O于K,延长AH交⊙O于W,连接BW,则OR∥CD,AR=KR=AK,AW是直径,由题意设AD=20x(x>0),则CD=15x,得出DG=AG=10x,DE=GE=5x,证出∠BED=∠ACD,由三角函数定义得出BD=DE=x,由勾股定理得出AB=x,得出∠ABW=90°,由相交线定理求出DK=5x,得出AK=AD+DK=25x,AR=x,求出GR=AR﹣AG=x,由三角函数定义求出AW=AB=x,由勾股定理得出KW=x,由三角形中位线定理得出OR=KW=x,在Rt△OGR中,由勾股定理得出方程:(x)2+(x)2=()2,解方程得出OR=,AR=,CD=15x=9,AD=20x=12,证明△AOR∽△AHD,得出=,得出DH=4,即可得出CH的长.
【解答】(1)证明:如图(1)中,延长BO交⊙O于E,连接AE.
∵BE是直径,
∴∠BAE=90°,
∴∠ABO+∠E=90°,
∵AD⊥BC,
∴∠ADC=90°,
∴∠DAC+∠C=90°,
∵∠E=∠C,
∴∠CAD=∠ABO.
(2)解:如图(2)中,过点O作OT⊥AC于T.
∵AD⊥BC,
由(1)可知,∠OAT=∠BAD,
∵∠ADB=∠ATO=90°,
∴△ADB∽△ATO,
∴=,
∵∠ADC=90°,
∴tan∠ACB==,
∴可以假设AD=4k,CD=3k,则AC=5k,
∵OT⊥AC,
∴AT=CT=k,
∴==.
(3)如图3中,作OR⊥AD于R,延长AD交⊙O于K,延长AH交⊙O于W,连接BW,则OR∥CD,AR=KR=AK,AW是直径,
由(1)得:∠ADC=90°,
∵tan∠ACB==,
∴设AD=20x(x>0),则CD=15x,
∵E是GD中点,G是AD中点,
∴DG=AG=10x,DE=GE=5x,
由(2)得:BM⊥AC,
∴∠CBF+∠AD=∠CBF+∠BED=90°,
∴∠BED=∠ACD,
∴tan∠BED==,
∴BD=DE=x,
∴AB===x,
∴∠ABW=90°,
由相交线定理得:AD×DK=BD×CD,
∴DK===5x,
∴AK=AD+DK=25x,AR=x,
∴GR=AR﹣AG=x,
∵∠ABW=90°,∠W=∠ACB,tan∠ACB=,
∴sinW==,
∴AW=AB=x,
∴KW===x,
∵AR=KR,OA=OW,
∴OR是△AKW的中位线,
∴OR=KW=x,
在Rt△OGR中,由勾股定理得:(x)2+(x)2=()2,
解得:x=,
∴OR=,AR=,CD=15x=9,AD=20x=12,
∵OR∥CD,
∴△AOR∽△AHD,
∴=,即=,
解得:DH=4,
∴CH=CD﹣DH=9﹣4=5.
27.抛物线y=ax2﹣6ax+4(a≠0)交y轴正半轴于点C,交x轴负半轴于点A,交x轴正半轴于点B,且AB=10.
(1)如图(1),求抛物线的解析式;
(2)如图(2),连接BC,点P为第一象限抛物线上一点,设点P横坐标为t,△PBC的面积为S,求S与t之间的函数关系式(不用写出自变量t的取值范围);
(3)如图(3),在(2)的条件下,连接PA交y轴于点D,过点P作x轴的垂线,分别交x轴于点E,交BC于点F,连接DF,当∠APE+∠CFD=90°时,在抛物线上是否存在点Q,使得点Q、PE的中点N、点C、是构成以CN为斜边的等腰直角三角形,若存在,请求出点Q的坐标,若不存在,请说明理由.
【分析】(1)设A(m,0),B(n,0),由题意:,求出点A的坐标,再利用待定系数法求出a即可.
(2)如图2中,连接OP.设P(t,﹣t2+t+4),根据S=S△POC+S△POB﹣S△OBC,求解即可.
(3)存在.如图3中,设P(m,﹣m2+m+4),首先证明DF∥AB,证明∠PAB=∠CFD=∠CBO,推出tan∠CBO=tan∠PAB==,求出点D的坐标,构建方程求出m的值,再求出点N的坐标,根据等腰直角三角形的性质,利用图象法求出满足条件的点Q的坐标,证明点Q在抛物线上,即可解决问题.
【解答】解:(1)如图1中,设A(m,0),B(n,0),
由题意:,
解得,
∴A(﹣2,0),B(8,0),
把A(﹣2,0)代入y=ax2﹣6ax+4,得到a=﹣,
∴抛物线的解析式为y=﹣x2+x+4.
(2)如图2中,连接OP.设P(t,﹣t2+t+4),
∵B(8,0),C(0,4),
∴OB=8,OC=4,
∴S=S△POC+S△POB﹣S△OBC=×4×t+×8×(﹣t2+t+4)﹣×4×8=﹣t2+8t(0<t<8).
(3)存在.
理由:如图3中,设P(m,﹣m2+m+4),
∵A(﹣2,0),B(8,0),C(0,4),
∴直线PA的解析式为y=﹣(m﹣8)x﹣m+4,直线BC的解析式为y=﹣x+4,
∵PE⊥x轴,
∴F(m,﹣m+4),
∵D(0,﹣m+4),
∴FD∥AB,
∴∠CFD=∠CBA,
∵∠APF+∠CFD=90°,∠APF+∠PAE=90°,
∴∠PAB=∠CFD=∠CBO,
∴tan∠CBO=tan∠PAB==,
∴=,
∵OA=2,
∴OD=1,
∴﹣m+4=1,
∴m=6,
∴P(6,4),E(6,0),
∵PN=NE,
∴N(6,2),
∵C(0,4),△CNQ是等腰直角三角形,CN是斜边,
当点Q在CN的上方时,如图3,过点Q作x轴的平行线交y轴于点G,交EP的延长线于点H,
设点Q(s,t),
易证△QGC≌△NHQ(AAS),
则GC=QH,GQ=HN,
即s=t﹣2,t﹣4=6﹣s,解得,
∴点Q的坐标为(4,6),
∵当x=4时,y=﹣×42+×4+4=6,
∴点Q在抛物线y=﹣x2+x+4上,
∴满足条件的点Q的坐标为(4,6).
一、选择题(每题3分,共计30分)
1.﹣3的倒数是( )
A. B.﹣ C.3 D.﹣3
2.下列运算正确的是( )
A.6a﹣5a=1 B.(a2)3=a5
C.3a2+2a3=5a5 D.a6?a2=a8
3.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
4.下列几何体各自的三视图中,只有两个视图相同的是( )
A.①③ B.②③ C.③④ D.②④
5.将抛物线y=x2向右平移3个单位长度,再向上平移2个单位长度,得到的抛物线的函数表达式为( )
A.y=(x+3)2﹣2 B.y=(x﹣3)2+2 C.y=(x+3)2+2 D.y=(x﹣3)2﹣2
6.如图,在地面上的点A处测得树顶B的仰角为α,AC=2,则树高BC为( )(用含α的代数式表示)
A.2sinα B.2tanα C.2cosα D.
7.如图,BM为⊙O的切线,点B为切点,点A、C在⊙O上,连接AB、AC、BC,若∠MBA=130°,则∠ACB的度数为( )
A.40° B.50° C.60° D.70°
8.抛物线y=x2+2x+1的对称轴是( )
A.直线x=1 B.直线x=﹣1 C.直线y=1 D.直线y=﹣1
9.某商品经过连续两次降价,售价由原来的每件25元降到每件16元,则平均每次降价的百分率为( )
A.20% B.40% C.18% D.36%
10.如图,四边形ABCD是平行四边形,点E在BA的延长线上,点F在BC的延长线上,连接EF,分别交AD,CD于点G,H,则下列结论错误的是( )
A.= B.= C.= D.=
二、填空题(每小题3分,共计30分)
11.将20300000用科学记数法表示为 .
12.在函数y=中,自变量x的取值范围是 .
13.计算2+的结果为 .
14.不等式组的解集是 .
15.反比例函数的图象在每个象限内,y随x的增大而增大,则a的值可以是 .(写出一个符合条件的实数即可)
16.一个扇形的圆心角是120°.它的半径是3cm.则扇形的弧长为 cm.
17.汽车刹车后行驶的距离s米与行驶的时间t秒的函数关系式是s=30t﹣6t2,汽车刹车后到停下来前进了 米.
18.如图,在平面直角坐标中,点O为坐标原点,直线y=kx﹣2k(k<0)交x轴的正半轴于点A,交y轴的正半轴于点B,若BC平分∠ABO交OA于点C,AC=2OC,则k的值为 .
19.如图,在矩形ABCD中,AB=6,BC=8,E、F分别是AD、BC的中点,G是对角线AC上的点,∠EGF=90°,则AG的长为 .
20.如图,△ABC中,CA=CB,点E在BC边上,点D在AC边上,连接AE、DE,若AB=AE,2∠AEB+∠ADE=180°,BE=8,CD=,则CE= .
三、解答题(21、22题每题7分,23、24题每题8分,25、26、27题每题10分)
21.先化简,再求值:(1﹣)÷,其中x=3tan30°+2cos60°.
22.如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点三角形ABC(顶点是网格线的交点).
(1)先将△ABC竖直向上平移6个单位,再水平向右平移3个单位得到△A1B1C1,点A、B、C对应点分别是A1、B1、C1,请画出△A1B1C1;
(2)将△A1B1C1绕B1点顺时针旋转90°,得△A2B1C2,点A1、C1对应点分别是A2、C2,请画出△A2B1C2;
(3)连接CA2,直接写出CA2的长 .
23.某社区为了调查居民对“物业管理”的满意度,随机抽取了部分居民作问卷调查:用“A”表示“相当满意”,“B”表示“满意”,“C”表示“比较满意”,“D”表示“不满意”,下图是工作人员根据问卷调查统计资料绘制的两幅不完整的统计图,请你根据统计图提供的信息解答以下问题:
(1)本次问卷调查,共调查了多少人.
(2)将图(2)中“B”部分的图形补充完整.
(3)如果该社区有居民2000人,请你估计该社区居民对“物业管理”感到“不满意”的约有多少人?
24.如图1,在△ABC和△ADE中,∠BAC=∠EAD,AB=AC,AD=AE,连接CD、AE交于点F.
(1)求证:∠DCE=∠BAC;
(2)当∠BAC=∠EAD=30°,AD⊥AB时(如图2),延长DC、AB交于点G,请直接写出图中除△ABC、△ADE以外的等腰三角形.
25.某商店计划今年的圣诞节购进A、B两种纪念品若干件.若花费480元购进的A种纪念品的数量是花费480元购进B种纪念品的数量的,已知每件A种纪念品比每件B种纪念品多4元.
(1)求购买一件A种纪念品、一件B种纪念品各需多少元?
(2)若商店一次性购买A、B纪念品共200件,要使总费用不超过3000元,最少要购买多少件B种纪念品?
26.△ABC内接于⊙O,AD⊥BC于点D.
(1)如图(1),连接OB,求证:∠CAD=∠ABO;
(2)如图(2),BE⊥AC于点E交AD于F,tan∠ACB=,连接OA,求的值;
(3)如图(3),在(2)的条件下,延长AO交BC于H,点G在AF上,且FD=GF,GA=GD,连接OG、EH,若OG=,求EH的长.
27.抛物线y=ax2﹣6ax+4(a≠0)交y轴正半轴于点C,交x轴负半轴于点A,交x轴正半轴于点B,且AB=10.
(1)如图(1),求抛物线的解析式;
(2)如图(2),连接BC,点P为第一象限抛物线上一点,设点P横坐标为t,△PBC的面积为S,求S与t之间的函数关系式(不用写出自变量t的取值范围);
(3)如图(3),在(2)的条件下,连接PA交y轴于点D,过点P作x轴的垂线,分别交x轴于点E,交BC于点F,连接DF,当∠APE+∠CFD=90°时,在抛物线上是否存在点Q,使得点Q、PE的中点N、点C、是构成以CN为斜边的等腰直角三角形,若存在,请求出点Q的坐标,若不存在,请说明理由.
2020-2021学年黑龙江省哈尔滨市部分学校九年级(上)期中数学试卷(五四学制)
参考答案与试题解析
一.选择题(共10小题)
1.﹣3的倒数是( )
A. B.﹣ C.3 D.﹣3
【分析】根据倒数的概念:乘积是1的两数互为倒数可得答案.
【解答】解:﹣3的倒数是﹣,
故选:B.
2.下列运算正确的是( )
A.6a﹣5a=1 B.(a2)3=a5
C.3a2+2a3=5a5 D.a6?a2=a8
【分析】结合幂的乘方与积的乘方的概念和运算法则进行求解即可.
【解答】解:A、6a﹣5a=a≠1,本选项错误;
B、(a2)3=a6≠a5,本选项错误;
C、3a2+2a3≠5a5,本选项错误;
D、a6?a2=a8,本选项正确.
故选:D.
3.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
【分析】根据轴对称图形与中心对称图形的概念求解.
【解答】解:A、是轴对称图形,也是中心对称图形,故此选项正确;
B、不是轴对称图形,也不是中心对称图形,故此选项错误;
C、是轴对称图形,不是中心对称图形,故此选项错误;
D、不是轴对称图形,是中心对称图形,故此选项错误;
故选:A.
4.下列几何体各自的三视图中,只有两个视图相同的是( )
A.①③ B.②③ C.③④ D.②④
【分析】分别分析四个几何体的三视图,从中找出只有两个视图相同的几何体,可得出结论.
【解答】解:①正方形的主、左和俯视图都是正方形;
②圆锥的主、左视图是三角形,俯视图是显示圆心的圆;
③球体的主、左和俯视图都是圆形;
④圆柱的主、左视图是长方形,俯视图是圆;
只有两个视图相同的几何体是圆锥和圆柱体.
故选:D.
5.将抛物线y=x2向右平移3个单位长度,再向上平移2个单位长度,得到的抛物线的函数表达式为( )
A.y=(x+3)2﹣2 B.y=(x﹣3)2+2 C.y=(x+3)2+2 D.y=(x﹣3)2﹣2
【分析】根据二次函数变化规律:左加右减,上加下减,进而得出变化后解析式.
【解答】解:∵抛物线y=x2向右平移3个单位长度,再向上平移2个单位长度,
∴平移后的解析式为:y=(x﹣3)2+2.
故选:B.
6.如图,在地面上的点A处测得树顶B的仰角为α,AC=2,则树高BC为( )(用含α的代数式表示)
A.2sinα B.2tanα C.2cosα D.
【分析】根据题意可知BC⊥AC,在Rt△ABC中,AC=7米,∠BAC=α,利用锐角三角函数的定义即可求出BC的高度.
【解答】解:∵BC⊥AC,AC=2,∠BAC=α,
∴tanα=,
∴BC=AC?tanα=2tanα,
故选:B.
7.如图,BM为⊙O的切线,点B为切点,点A、C在⊙O上,连接AB、AC、BC,若∠MBA=130°,则∠ACB的度数为( )
A.40° B.50° C.60° D.70°
【分析】直接利用切线的性质得出∠OBM=90°,求出∠AOB的度数,进而利用圆周角定理可得出答案.
【解答】解:如图,连接OA,OB,
∵BM为⊙O的切线,
∴∠OBM=90°,
∵∠MBA=130°,
∴∠ABO=40°,
∵OA=OB,
∴∠BAO=∠ABO=40°,
∴∠AOB=180°﹣40°﹣40°=100°,
∴∠ACB=∠AOB=50°,
故选:B.
8.抛物线y=x2+2x+1的对称轴是( )
A.直线x=1 B.直线x=﹣1 C.直线y=1 D.直线y=﹣1
【分析】由对称轴公式﹣可得对称轴.
【解答】解:∵对称轴x=﹣=﹣=﹣1,
∴对称轴是直线x=﹣1.
故选:B.
9.某商品经过连续两次降价,售价由原来的每件25元降到每件16元,则平均每次降价的百分率为( )
A.20% B.40% C.18% D.36%
【分析】设降价的百分率为x,根据降低率的公式a(1﹣x)2=b建立方程,求解即可.
【解答】解:设降价的百分率为x
根据题意可列方程为25(1﹣x)2=16
解方程得,(舍)
∴每次降价的百分率为20%
故选:A.
10.如图,四边形ABCD是平行四边形,点E在BA的延长线上,点F在BC的延长线上,连接EF,分别交AD,CD于点G,H,则下列结论错误的是( )
A.= B.= C.= D.=
【分析】根据相似三角形的判定和性质进行判断即可.
【解答】解:∵四边形ABCD是平行四边形,
∴AD∥BF,BE∥DC,AD=BC,
∴,,,
故选:C.
二.填空题
11.将20300000用科学记数法表示为 2.03×107 .
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数;当原数的绝对值<1时,n是负整数.
【解答】解:数字20300000科学记数法可表示为2.03×107.
故答案为:2.03×107.
12.在函数y=中,自变量x的取值范围是 x≠2 .
【分析】根据函数表达式是整式时,自变量可取全体实数解答.
【解答】解:当x﹣2≠0,即x≠2时,函数y=有意义.
故答案为:全x≠2.
13.计算2+的结果为 3 .
【分析】首先化简二次根式,进而合并求出答案.
【解答】解:原式=2×+2=3.
故答案为:3.
14.不等式组的解集是 x≤2 .
【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
【解答】解:解不等式6﹣3x≥0,得:x≤2,
解不等式2x<x+4,得:x<4,
则不等式组的解集为x≤2,
故答案为x≤2.
15.反比例函数的图象在每个象限内,y随x的增大而增大,则a的值可以是 ﹣4 .(写出一个符合条件的实数即可)
【分析】根据反比例函数的性质解答.
【解答】解:依题意有a+3<0,则a<﹣3.故a的值可以是﹣4.(答案不唯一,符合条件的实数即可.)
16.一个扇形的圆心角是120°.它的半径是3cm.则扇形的弧长为 2π cm.
【分析】根据弧长公式可得结论.
【解答】解:根据题意,扇形的弧长为=2π,
故答案为:2π
17.汽车刹车后行驶的距离s米与行驶的时间t秒的函数关系式是s=30t﹣6t2,汽车刹车后到停下来前进了 米.
【分析】利用配方法求二次函数最值的方法解答即可.
【解答】解:∵s=30t﹣6t2=﹣6(t﹣)2+,
∴汽车刹车后到停下来前进了m.
故答案为:.
18.如图,在平面直角坐标中,点O为坐标原点,直线y=kx﹣2k(k<0)交x轴的正半轴于点A,交y轴的正半轴于点B,若BC平分∠ABO交OA于点C,AC=2OC,则k的值为 ﹣ .
【分析】过点C作CD⊥AB于点D,则OC=CD,利用面积法结合AB=2OC,可得出AB=2OA,利用勾股定理可得出OA=OB,利用一次函数图象上点的坐标特征可求出OA,OB的长,结合OA=OB可求出k值.
【解答】解:过点C作CD⊥AB于点D,则OC=CD,如图所示.
∵S△BOC=OC?OB,S△ABC=AC?OB=AB?CD,
∴===2,
∴AB=2OB,
∴OA==OB.
当x=0时,直线y=kx﹣2k=﹣2k,
∴OB=﹣2k;
当y=0时,y=kx﹣2k=0,解得:x=2,
∴OA=2,
∴2=×(﹣2k),
∴k=﹣.
故答案为:﹣.
19.如图,在矩形ABCD中,AB=6,BC=8,E、F分别是AD、BC的中点,G是对角线AC上的点,∠EGF=90°,则AG的长为 2或8 .
【分析】连接EF交AC于O,先证四边形ABFE是矩形,得EF=AB=6,EF∥AB,再证OF是△ABC的中位线,得OA=OC=AC=5,然后由直角三角形的性质得OG=EF=3,分两种情况求出即可.
【解答】解:如图,连接EF交AC于点O,
∵四边形ABCD是矩形,
∴∠B=∠BAD=90°,AD=BC=8,AD∥BC,
∴AC===10,
∵E、F分别是AD、BC的中点,
∴AE=BF=4,AE∥BF,
∴四边形ABFE是平行四边形,
∵∠BAE=90°,
∴四边形ABFE是矩形,
∴EF=AB=6,EF∥AB,
∴OF是△ABC的中位线,
∴OA=OC=AC=5,
∵∠EGF=90°,
∴OG=EF=3,
当点G在线段OA上时,AG=OA﹣OG=2,
当点G在线段OC上时,AG′=OA+OG'=8;
故答案为:2或8.
20.如图,△ABC中,CA=CB,点E在BC边上,点D在AC边上,连接AE、DE,若AB=AE,2∠AEB+∠ADE=180°,BE=8,CD=,则CE= 12 .
【分析】过点A作AM⊥BE于E,过点D作DN⊥EC于N,由等腰三角形的性质和三角形内角和定理可求∠C=∠DEC,可得DE=DC=,通过证明△CDN∽△CAM,可得,即可求解.
【解答】解:如图,过点A作AM⊥BE于E,过点D作DN⊥EC于N,
∵CA=CB,AB=AE,
∴∠B=∠CAB,∠B=∠AEB,
∴∠B=∠CAB=∠AEB,
∵∠B+∠BAC+∠C=180°,∠B+∠AEB+∠BAE=180°,
∴∠C=∠BAE,
∴2∠AEB+∠C=180°,
又∵2∠AEB+∠ADE=180°,
∴∠C=∠ADE,
又∵∠ADE=∠C+∠DEC,
∴∠C=∠DEC,
∴DE=DC=,
∵AB=AE,AM⊥BE,DE=CC,DN⊥EC,
∴BM=ME=BE=4,EN=NC=EC,AM∥DN,
∴△CDN∽△CAM,
∴,
∴,
∴EC=12,EC=﹣5(不合题意舍去),
故答案为:12.
三.解答题(共7小题)
21.先化简,再求值:(1﹣)÷,其中x=3tan30°+2cos60°.
【分析】先根据分式混合运算的法则把原式进行化简,再求出x的值代入进行计算即可.
【解答】解:原式=?
=,
∵x=3×+2×=+1,
∴原式===.
22.如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点三角形ABC(顶点是网格线的交点).
(1)先将△ABC竖直向上平移6个单位,再水平向右平移3个单位得到△A1B1C1,点A、B、C对应点分别是A1、B1、C1,请画出△A1B1C1;
(2)将△A1B1C1绕B1点顺时针旋转90°,得△A2B1C2,点A1、C1对应点分别是A2、C2,请画出△A2B1C2;
(3)连接CA2,直接写出CA2的长 .
【分析】(1)将点A、B、C分别向上平移6个单位、向右平移3个单位得到平移后的对应点,再首尾顺次连接即可;
(2)将点A1、C1分别绕B1点顺时针旋转90得到对应点,再与点B1首尾顺次连接即可;
(3)利用勾股定理求解即可.
【解答】解:(1)如图所示,△A1B1C1即为所求.
(2)如图所示,△A2B1C2即为所求.
(3)CA2==,
故答案为:.
23.某社区为了调查居民对“物业管理”的满意度,随机抽取了部分居民作问卷调查:用“A”表示“相当满意”,“B”表示“满意”,“C”表示“比较满意”,“D”表示“不满意”,下图是工作人员根据问卷调查统计资料绘制的两幅不完整的统计图,请你根据统计图提供的信息解答以下问题:
(1)本次问卷调查,共调查了多少人.
(2)将图(2)中“B”部分的图形补充完整.
(3)如果该社区有居民2000人,请你估计该社区居民对“物业管理”感到“不满意”的约有多少人?
【分析】(1)根据条形图可得C人数为100人,根据扇形图可得C占总人数的20%,再用100除以20%可得答案;
(2)首先利用总数减去各条的纵坐标可得答案;
(3)利用样本估计总体的方法用2000乘以感到“不满意”的人数所占百分比.
【解答】解:(1)100÷20%=500(人),
本次问卷调查,共调查了500人.
(2)500﹣200﹣100﹣50=150(人),
如图.
(3)如果该校有学生2000人,则该校学生对教学感到“不满意”的约有:2000×10%=200(人).
24.如图1,在△ABC和△ADE中,∠BAC=∠EAD,AB=AC,AD=AE,连接CD、AE交于点F.
(1)求证:∠DCE=∠BAC;
(2)当∠BAC=∠EAD=30°,AD⊥AB时(如图2),延长DC、AB交于点G,请直接写出图中除△ABC、△ADE以外的等腰三角形.
【分析】(1)如图1,先证明△ACD≌△ABE,得∠ACD=∠ABC,根据三角形内角和与平角定义得出结论;
(2)如图2,图形中有四个等腰三角形:分别是①△ACF是等腰三角形,②△ADG是等腰直角三角形,③△DEF是等腰三角形;④△ECD是等腰三角形;根据已知角的度数依次计算各角的度数,根据两个角相等的三角形是等腰三角形得出结论.
【解答】证明:(1)如图1,∵∠BAC=∠EAD,
∴∠BAC+∠CAE=∠EAD+∠CAE,
即∠BAE=∠CAD,
∵AB=AC,AD=AE,
∴△ACD≌△ABE,
∴∠ACD=∠ABC,
∵∠BAC+∠ABC+∠ACB=180°,
∠ECD+∠ACD+∠ACB=180°,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠BAC+2∠ACB=180°,
∠ECD+2∠ACB=180°,
∴∠BAC=∠ECD;
(2)如图2,
①∵∠BAC=∠EAD=30°,
∴∠ABC=∠ACB=∠AED=∠ADE=75°,
由(1)得:∠ACD=∠ABC=75°,
∠DCE=∠BAC=30°,
∵AD⊥AB,
∴∠BAD=90°,
∴∠CAE=30°,
∴∠AFC=180°﹣30°﹣75°=75°,
∴∠ACF=∠AFC,
∴△ACF是等腰三角形,
②∵∠BCG=∠DCE=30°,∠ABC=75°,
∴∠G=45°,
在Rt△AGD中,∠ADG=45°,
∴△ADG是等腰直角三角形,
③∠EDF=75°﹣45°=30°,
∴∠DEF=∠DFE=75°,
∴△DEF是等腰三角形;
④∵∠ECD=∠EDC=30°,
∴△ECD是等腰三角形.
25.某商店计划今年的圣诞节购进A、B两种纪念品若干件.若花费480元购进的A种纪念品的数量是花费480元购进B种纪念品的数量的,已知每件A种纪念品比每件B种纪念品多4元.
(1)求购买一件A种纪念品、一件B种纪念品各需多少元?
(2)若商店一次性购买A、B纪念品共200件,要使总费用不超过3000元,最少要购买多少件B种纪念品?
【分析】(1)设购买一件B种纪念品需x元,则购买一件A种纪念品需(x+4)元,根据数量=总价÷单价结合花费480元购进的A种纪念品的数量是花费480元购进B种纪念品的数量的,即可得出关于x的分式方程,解之经检验后即可得出结论;
(2)设购买m件B种纪念品,则购买(200﹣m)件A种纪念品,根据总价=单价×数量结合要使总费用不超过3000元,即可得出关于m的一元一次不等式,解之取其中的最小值即可得出结论.
【解答】解:(1)设购买一件B种纪念品需x元,则购买一件A种纪念品需(x+4)元,
依题意,得:=×,
解得:x=12,
经检验,x=12是原方程的解,且符合题意,
∴x+4=16.
答:购买一件A种纪念品需16元,购买一件B种纪念品需12元.
(2)设购买m件B种纪念品,则购买(200﹣m)件A种纪念品,
依题意,得:16(200﹣m)+12m≤3000,
解得:m≥50.
答:最少要购买50件B种纪念品.
26.△ABC内接于⊙O,AD⊥BC于点D.
(1)如图(1),连接OB,求证:∠CAD=∠ABO;
(2)如图(2),BE⊥AC于点E交AD于F,tan∠ACB=,连接OA,求的值;
(3)如图(3),在(2)的条件下,延长AO交BC于H,点G在AF上,且FD=GF,GA=GD,连接OG、EH,若OG=,求EH的长.
【分析】(1)如图,延长BO交⊙O于E,连接AE.利用等角的余角相等解决问题即可.
(2)如图(2)中,过点O作OT⊥AC于T.证明△ADB∽△ATO,可得=,解决问题.
(3)如图3中,作OR⊥AD于R,延长AD交⊙O于K,延长AH交⊙O于W,连接BW,则OR∥CD,AR=KR=AK,AW是直径,由题意设AD=20x(x>0),则CD=15x,得出DG=AG=10x,DE=GE=5x,证出∠BED=∠ACD,由三角函数定义得出BD=DE=x,由勾股定理得出AB=x,得出∠ABW=90°,由相交线定理求出DK=5x,得出AK=AD+DK=25x,AR=x,求出GR=AR﹣AG=x,由三角函数定义求出AW=AB=x,由勾股定理得出KW=x,由三角形中位线定理得出OR=KW=x,在Rt△OGR中,由勾股定理得出方程:(x)2+(x)2=()2,解方程得出OR=,AR=,CD=15x=9,AD=20x=12,证明△AOR∽△AHD,得出=,得出DH=4,即可得出CH的长.
【解答】(1)证明:如图(1)中,延长BO交⊙O于E,连接AE.
∵BE是直径,
∴∠BAE=90°,
∴∠ABO+∠E=90°,
∵AD⊥BC,
∴∠ADC=90°,
∴∠DAC+∠C=90°,
∵∠E=∠C,
∴∠CAD=∠ABO.
(2)解:如图(2)中,过点O作OT⊥AC于T.
∵AD⊥BC,
由(1)可知,∠OAT=∠BAD,
∵∠ADB=∠ATO=90°,
∴△ADB∽△ATO,
∴=,
∵∠ADC=90°,
∴tan∠ACB==,
∴可以假设AD=4k,CD=3k,则AC=5k,
∵OT⊥AC,
∴AT=CT=k,
∴==.
(3)如图3中,作OR⊥AD于R,延长AD交⊙O于K,延长AH交⊙O于W,连接BW,则OR∥CD,AR=KR=AK,AW是直径,
由(1)得:∠ADC=90°,
∵tan∠ACB==,
∴设AD=20x(x>0),则CD=15x,
∵E是GD中点,G是AD中点,
∴DG=AG=10x,DE=GE=5x,
由(2)得:BM⊥AC,
∴∠CBF+∠AD=∠CBF+∠BED=90°,
∴∠BED=∠ACD,
∴tan∠BED==,
∴BD=DE=x,
∴AB===x,
∴∠ABW=90°,
由相交线定理得:AD×DK=BD×CD,
∴DK===5x,
∴AK=AD+DK=25x,AR=x,
∴GR=AR﹣AG=x,
∵∠ABW=90°,∠W=∠ACB,tan∠ACB=,
∴sinW==,
∴AW=AB=x,
∴KW===x,
∵AR=KR,OA=OW,
∴OR是△AKW的中位线,
∴OR=KW=x,
在Rt△OGR中,由勾股定理得:(x)2+(x)2=()2,
解得:x=,
∴OR=,AR=,CD=15x=9,AD=20x=12,
∵OR∥CD,
∴△AOR∽△AHD,
∴=,即=,
解得:DH=4,
∴CH=CD﹣DH=9﹣4=5.
27.抛物线y=ax2﹣6ax+4(a≠0)交y轴正半轴于点C,交x轴负半轴于点A,交x轴正半轴于点B,且AB=10.
(1)如图(1),求抛物线的解析式;
(2)如图(2),连接BC,点P为第一象限抛物线上一点,设点P横坐标为t,△PBC的面积为S,求S与t之间的函数关系式(不用写出自变量t的取值范围);
(3)如图(3),在(2)的条件下,连接PA交y轴于点D,过点P作x轴的垂线,分别交x轴于点E,交BC于点F,连接DF,当∠APE+∠CFD=90°时,在抛物线上是否存在点Q,使得点Q、PE的中点N、点C、是构成以CN为斜边的等腰直角三角形,若存在,请求出点Q的坐标,若不存在,请说明理由.
【分析】(1)设A(m,0),B(n,0),由题意:,求出点A的坐标,再利用待定系数法求出a即可.
(2)如图2中,连接OP.设P(t,﹣t2+t+4),根据S=S△POC+S△POB﹣S△OBC,求解即可.
(3)存在.如图3中,设P(m,﹣m2+m+4),首先证明DF∥AB,证明∠PAB=∠CFD=∠CBO,推出tan∠CBO=tan∠PAB==,求出点D的坐标,构建方程求出m的值,再求出点N的坐标,根据等腰直角三角形的性质,利用图象法求出满足条件的点Q的坐标,证明点Q在抛物线上,即可解决问题.
【解答】解:(1)如图1中,设A(m,0),B(n,0),
由题意:,
解得,
∴A(﹣2,0),B(8,0),
把A(﹣2,0)代入y=ax2﹣6ax+4,得到a=﹣,
∴抛物线的解析式为y=﹣x2+x+4.
(2)如图2中,连接OP.设P(t,﹣t2+t+4),
∵B(8,0),C(0,4),
∴OB=8,OC=4,
∴S=S△POC+S△POB﹣S△OBC=×4×t+×8×(﹣t2+t+4)﹣×4×8=﹣t2+8t(0<t<8).
(3)存在.
理由:如图3中,设P(m,﹣m2+m+4),
∵A(﹣2,0),B(8,0),C(0,4),
∴直线PA的解析式为y=﹣(m﹣8)x﹣m+4,直线BC的解析式为y=﹣x+4,
∵PE⊥x轴,
∴F(m,﹣m+4),
∵D(0,﹣m+4),
∴FD∥AB,
∴∠CFD=∠CBA,
∵∠APF+∠CFD=90°,∠APF+∠PAE=90°,
∴∠PAB=∠CFD=∠CBO,
∴tan∠CBO=tan∠PAB==,
∴=,
∵OA=2,
∴OD=1,
∴﹣m+4=1,
∴m=6,
∴P(6,4),E(6,0),
∵PN=NE,
∴N(6,2),
∵C(0,4),△CNQ是等腰直角三角形,CN是斜边,
当点Q在CN的上方时,如图3,过点Q作x轴的平行线交y轴于点G,交EP的延长线于点H,
设点Q(s,t),
易证△QGC≌△NHQ(AAS),
则GC=QH,GQ=HN,
即s=t﹣2,t﹣4=6﹣s,解得,
∴点Q的坐标为(4,6),
∵当x=4时,y=﹣×42+×4+4=6,
∴点Q在抛物线y=﹣x2+x+4上,
∴满足条件的点Q的坐标为(4,6).
同课章节目录
