2021年中考二轮复习数学《探索二次函数综合型压轴题解题技巧》分类训练五:与直角三角形相关的压轴题(附答案)
文档属性
| 名称 | 2021年中考二轮复习数学《探索二次函数综合型压轴题解题技巧》分类训练五:与直角三角形相关的压轴题(附答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 668.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-20 00:00:00 | ||
图片预览




文档简介
2021中考数学复习《探索二次函数综合型压轴题解题技巧》分类训练五:
与直角三角形相关的压轴题(附答案)
方法提炼(1):
1、利用坐标系中两点距离公式,得到所求三角形三边平方的代数式;
2、确定三角形中的直角顶点,若无法确定则分情况讨论;
3、根据勾股定理得到方程,然后解方程,若方程有解,此点存在;否则不存在;
方法提炼(2):
1、利用两直线垂直,K值互为负倒数(K1K2=-1),先确定点所在的直线表达式
2、将直线与抛物线的表达式联立方程组,若求出交点坐标,此点存在;否则不存在;
方法提炼(3):
1、利用特殊角45°构造直角三角形,易求点的坐标。
典例引领:
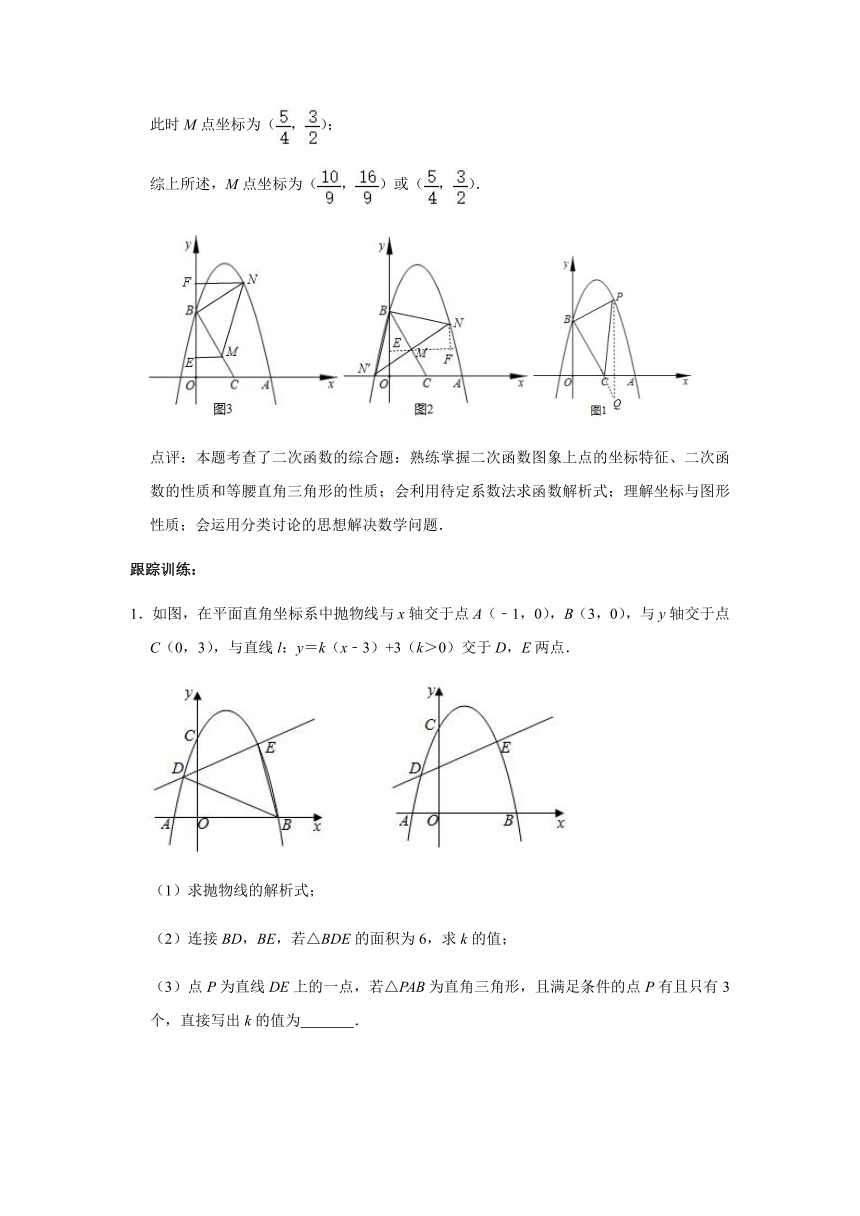
3.如图,抛物线y=﹣x2+bx+c经过A(4,0),B(0,4)两点,C为OA的中点,连接BC.
(1)求抛物线的解析式;
(2)P为第一象限抛物线上一点,连接PB,PC,当△PBC的面积为6时,求点P的坐标;
(3)M在线段BC上,在坐标平面内,以BM为直角边作等腰直角△BMN,当点N在抛物线上时,直接写出点M的坐标.
分析:(1)利用待定系数法求抛物线的解析式;
(2)作PQ∥y轴交直线BC于Q,如图1,先确定直线BC的解析式为y=﹣2x+4;设P(x,﹣x2+3x+4),则Q(x,﹣2x+4),所以PQ=﹣x2+5x,利用三角形面积公式得到S△PBC=S△PQB﹣S△PCQ=PQ,则﹣x2+5x=6,然后解方程求出x即可得到P点坐标;
(3)设M(t,﹣2t+4)(0<t≤2),当∠BMN=90°时,作ME⊥y轴于E,NF⊥EM于F,如图2,先证明△BME≌MNF得到ME=NF=t,BE=MF=2t,则N(3t,﹣t+4),接着把N(3t,﹣t+4)代入y=﹣x2+3x+4得﹣(3t)2+9t+4=﹣t+4;然后表示出点N关于点M的对称点N′的坐标为(﹣t,﹣3t+4),把N′(﹣t,﹣3t+4)代入y=﹣x2+3x+4得﹣(﹣t)2﹣3t+4=﹣3t+4;当∠MBN=90°时,作ME⊥y轴于E,NF⊥y轴于F,如图3,通过证明△BME≌NBF得到ME=BF=t,BE=NF=2t,则N(2t,t+4),然后把N(2t,t+4)代入y=﹣x2+3x+4得﹣(2t)2+6t+4=t+4,最后分别解关于t的方程可得到满足条件的M点坐标.
解:(1)解:根据题意得,解得:b=3,c=4,
抛物线的解析式为y=﹣x2+3x+4;
(2)∵C为OA的中点,
∴C点坐标是(2,0)
作PQ∥y轴交直线BC于Q,如图1,
设直线BC的解析式为y=mx+n,
把B(0,4),C(2,0)代入得,解得,
∴直线BC的解析式为y=﹣2x+4;
设P(x,﹣x2+3x+4),则Q(x,﹣2x+4),
∴PQ=﹣x2+3x+4﹣(﹣2x+4)=﹣x2+5x,
∵S△PBC=S△PQB﹣S△PCQ=PQ?2=PQ,
∴﹣x2+5x=6,
整理得x2﹣5x+6=0,解得x1=3,x2=2,
∴P点坐标为(3,4)或(2,6);
(3)设M(t,﹣2t+4)(0<t≤2),
当∠BMN=90°时,作ME⊥y轴于E,NF⊥EM于F,如图2,
∵△BMN为等腰直角三角形,
∴BM=MN,
易得△BME≌MNF(AAS),则ME=NF=t,BE=MF=4﹣(﹣2t+4)=2t,
∴N(3t,﹣t+4),
把N(3t,﹣t+4)代入y=﹣x2+3x+4得﹣(3t)2+9t+4=﹣t+4,解得t1=0(舍去),t2=,此时M点坐标为(,);
点N(3t,﹣t+4)关于点M(t,﹣2t+4)的对称点N′的坐标为(﹣t,﹣3t+4),
把N′(﹣t,﹣3t+4)代入y=﹣x2+3x+4得﹣(﹣t)2﹣3t+4=﹣3t+4,解得t1=t2=0(舍去);
当∠MBN=90°时,作ME⊥y轴于E,NF⊥y轴于F,如图3,
∵△BMN为等腰直角三角形,
∴BM=BN,
易得△BME≌NBF(AAS),则ME=BF=t,BE=NF=4﹣(﹣2t+4)=2t,
∴N(2t,t+4),
把N(2t,t+4)代入y=﹣x2+3x+4得﹣(2t)2+6t+4=t+4,解得t1=0(舍去),t2=,此时M点坐标为(,);
综上所述,M点坐标为(,)或(,).
点评:本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质和等腰直角三角形的性质;会利用待定系数法求函数解析式;理解坐标与图形性质;会运用分类讨论的思想解决数学问题.
跟踪训练:
1.如图,在平面直角坐标系中抛物线与x轴交于点A(﹣1,0),B(3,0),与y轴交于点C(0,3),与直线l:y=k(x﹣3)+3(k>0)交于D,E两点.
(1)求抛物线的解析式;
(2)连接BD,BE,若△BDE的面积为6,求k的值;
(3)点P为直线DE上的一点,若△PAB为直角三角形,且满足条件的点P有且只有3个,直接写出k的值为 .
2.如图1,二次函数y=ax2+bx﹣2(a≠0)的图象与x轴交于A(﹣4,0)、B(1,0)两点,与y轴交于点C.
(1)求这个二次函数的表达式:
(2)点M在该抛物线的对称轴上,当△ACM是直角三角形时,求点M的坐标;
(3)如图2,点D在y轴上,且CD=OA,连接AD,点E、F分别是线段OA,AD上的动点,求EF+OF的最小值.
3.如图,已知二次函数y=ax2+bx+4的图象与x轴交于点A(4,0)和点D(﹣1,0),与y轴交于点C,过点C作BC平行于x轴交抛物线于点B,连接AC
(1)求这个二次函数的表达式;
(2)点M从点O出发以每秒2个单位长度的速度向点A运动;点N从点B同时出发,以每秒1个单位长度的速度向点C运动,其中一个动点到达终点时,另一个动点也随之停动,过点N作NQ垂直于BC交AC于点Q,连结MQ
①求△AQM的面积S与运动时间t之间的函数关系式,写出自变量的取值范围;当t为何值时,S有最大值,并求出S的最大值;
②是否存在点M,使得△AQM为直角三角形?若存在,求出点M的坐标;若不存在,说明理由.
4.如图,二次函数y=ax2+4x+c(a≠0)的图象与x轴交A,B两点,与y轴交于点C,直线y=﹣2x﹣6经过点A,C.
(1)求该二次函数的解析式;
(2)点P为第三象限内抛物线上的一个动点,△APC的面积为S,试求S的最大值;
(3)若P为抛物线的顶点,且直角三角形APQ的直角顶点Q在y轴上,请直接写出点Q的坐标.
5.在平面直角坐标系中,抛物线y=+bx+c,经过点A(1,3)、B(0,1),过点A作x轴的平行线交抛物线于另一点C
(1)求抛物线的表达式及其顶点坐标;
(2)如图1,点G是BC上方抛物线上的一个动点,分别过点G作GH⊥BC于点H、作GE⊥x轴于点E,交BC于点F,在点G运动的过程中,△GFH的周长是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由;
(3)如图2,过A点的直线垂直x轴于点M,点N为直线AM上任意一点,当△BCN为直角三角形时,请直接写出点N的坐标.
6.二次函数y=ax2+bx+2的图象交x轴于点(﹣1,0),B(4,0)两点,交y轴于点C.动点M从点A出发,以每秒2个单位长度的速度沿AB方向运动,过点M作MN⊥x轴交直线BC于点N,交抛物线于点D,连接AC,设运动的时间为t秒.
(1)求二次函数y=ax2+bx+2的表达式;
(2)连接BD,当t=时,求△DNB的面积;
(3)在直线MN上存在一点P,当△PBC是以∠BPC为直角的等腰直角三角形时,求此时点D的坐标;
(4)当t=时,在直线MN上存在一点Q,使得∠AQC+∠OAC=90°,求点Q的坐标.
7.如图A(0,3),B(3,0),C(1,0)分别是抛物线:y=ax2+bx+c(a≠0)上的三点,点P为抛物线上一动点.
(1)求此抛物线的解析式.
(2)当△PAB是以AB为一直角边的直角三角形时,求此时点P的坐标.
(3)若点P在抛物线上A、B两点之间移动时,是否存在一个位置,使△PAB的面积最大?若存在,请求此时点P的坐标.若不存在,请说明理由.
8.如图,抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,3).
(1)求抛物线对应函数的关系式,及A点坐标.
(2)点D为抛物线对称轴上一点.
①当△BCD是以BC为直角边的直角三角形时,求点D的坐标;
②若△BCD是锐角三角形,求点D的纵坐标的取值范围.
9.已知抛物线经过点A(﹣1,0)、点B(3,0)、点C(0,3),点D为抛物线在第一象限内图象上一动点,连接AD,交y轴于点E,将点C关于线段AD作轴对称,对称点为C',连接AC'.
(1)求抛物线的解析式;
(2)如图1如果点C'落在x轴,求点E坐标;
(3)如图2,连接AC、BC,BC与AD交于点F,拖动点D,点C'落在第四象限,作FG∥AC,交x轴于点M,交AC'于点G,若∠AGF=90°,求点M的横坐标.
10.如图,抛物线y=ax2+bx+4交y轴于点A,并经过B(4,4)和C(6,0)两点,点D的坐标为(4,0),连接AD,BC,点F从点O出发,以每秒1个单位长度的速度沿线段OC方向运动,到达点C后停止运动:点M同时从点D出发以每秒1个单位长度的速度沿x轴正方向运动,当点F停止时点M也停止运动.设点F的运动时间为t秒,过点F作AB的垂线EF交直线AB于点E,交AD于点H.
(1)求抛物线的解析式;
(2)以线段EH为斜边向右作等腰直角△EHG,当点G落在第一象限内的抛物线上时,求出t的值;
(3)设△EFM与四边形ADCB重合时的面积为S,请直接写出S与t的函数关系式与相应的自变量t的取值范围.
11.如图,抛物线y=ax2+bx+2交x轴于点A(﹣3,0)和点B(1,0),交y轴于点C.
(1)求这个抛物线的函数表达式.
(2)点D的坐标为(﹣1,0),点P为第二象限内抛物线上的一个动点,求四边形ADCP面积的最大值.
(3)点M为抛物线对称轴上的点,问:在抛物线上是否存在点N,使△MNO为等腰直角三角形,且∠MNO为直角?若存在,请直接写出点N的坐标;若不存在,请说明理由.
12.如图①,已知抛物线y=ax2+bx+c的图象经过点A(0,3)、B(1,0),其对称轴为直线l:x=2,过点A作AC∥x轴交抛物线于点C,∠AOB的平分线交线段AC于点E,点P是抛物线上的一个动点,设其横坐标为m.
(1)若动点P在直线OE下方的抛物线上,连结PE、PO,当m为何值时,四边形AOPE面积最大?当四边形AOPE面积最大时,在抛物线对称轴直线上找一点M,使得MB+MP的值最小,求M的坐标;
(2)如图②,F是抛物线的对称轴l上的一点,在抛物线上是否存在点P使△POF成为以点P为直角顶点的等腰直角三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
13.已知直线y=x+4与x轴、y轴分别交于A、C两点,抛物线y=ax2+bx+c经过A、C两点,与x轴的另一个交点为B,且OC=2OB.
(1)求抛物线的解析式;
(2)点P在AO上,点Q在OC的延长线上,且AP=CQ,连接PQ交AC于点G,点D为第一象限内的一点,当△PDQ是以PQ为斜边的等腰直角三角形时,连接OD,设AP的长度为t,△POD的面积为S,请用含t的式子表示S,并写出自变量t的取值范围;
(3)在(2)的条件下,连接OG、DG,将△PGD沿PD翻折到PDK的位置(G与K对应),若OG=,求点K的坐标.
参考答案
1.解:(1)∵抛物线与x轴交于点A(﹣1,0),B(3,0),
∴设解析式为y=a(x+1)(x﹣3)
∵抛物线交y轴于点C(0,3)
∴﹣3a=3
∴a=﹣1
∴抛物线的解析式为y=﹣(x+1)(x﹣3)=﹣x2+2x+3
(2)直线l:y=k(x﹣3)+3,当x=3时,y=3
∴直线l过定点F(3,3)
如图1,连接BF,则BF⊥x轴,BF=3
设点D横坐标为x1,点E横坐标为x2,
∵ 整理得:x2+(k﹣2)x﹣3k=0
∴x1+x2=2﹣k,x1x2=﹣3k
∵S△BDE=S△BDF﹣S△BEF=BF?(3﹣x1)﹣BF?(3﹣x2)=BF?(x2﹣x1)=6
∴x2﹣x1=4
∵(x1+x2)2﹣4x1x2=(x2﹣x1)2
∴(2﹣k)2﹣4(﹣3k)=16
解得:k1=﹣﹣4(舍去) k2=﹣4
∴k的值为
(3)∵△PAB为直角三角形,且在直线DE上各有一个点P满足∠PAB=90°与∠PBA=90°
∴只有1个点P满足∠APB=90°
∴直线DE与以AB为直径的圆相切
如图2,取AB中点G(1,0),G为圆心,PG=BG=2
设P(p,kp﹣3k+3),
∴PG2=(p﹣1)2+(kp﹣3k+3)2=4
整理得:(k2+1)p2+(6k﹣6k2﹣2)p+9k2﹣18k+6=0
∵有一个且只有一个满足条件的点P
∴△=(6k﹣6k2﹣2)2﹣4(k2+1)(9k2﹣18k+6)=0
解得:k=
故答案为:
2.解:(1)将A(﹣4,0)、B(1,0)的坐标分别代入y=ax2+bx﹣2,得
,
解得,,
∴这个二次函数的函数表达式为y=x2+x﹣2.
(2)由x=0得y=﹣2,
∴C(0,﹣2).
抛物线的对称轴为直线x=,即直线x=﹣,
设点M的坐标为(﹣,m),
AM2=(﹣+4)2+m2=+m2,CM2=()2+(m+2)2=+(m+2)2,AC2=42+22=20,
①当∠CAM=90°时,AM2+AC2=CM2,
即+m2+20=+(m+2)2,
解得m=5,
∴M(﹣,5),
②当∠ACM=90°时,AC2+CM2=AM2,即20++(m+2)2=+m2.解得m=﹣5,
∴M(﹣,﹣5),
③当∠AMC=90°时,AM2+CM2=AC2,即+m2++(m+2)2=20,
解得m1=,m2=,
∴M(﹣,)或(﹣,).
综上可知:点M的坐标为(﹣,5)、(﹣,﹣5)、(﹣,)或(﹣,).
(3)如图,作点O关于直线AD的对称点O′,过O′作O′H⊥OA于点H,则EF+OF的最小值为线段O′H的长.
连接OO′交AD于点M,则OO′⊥AD,且M是线段OO′的中点,
∵CD=OA=4,OC=2,
∴OD=2,
即点D的坐标为(0,2),
在Rt△AOD中,AD=,
∴sin∠DAO=,
∴OM=OA?sin∠DAO=4×=,
∴OO′=,
∴OH=OO′?sin∠OO′H=OO′?sin∠DAO=?=,
∴O′H=,
∴点O′(﹣,),
∴EF+OF的最小值=O′H=.
3.解:(1)∵二次函数的图象经过A(4,0)和点D(﹣1,0),
∴,
解得,
所以,二次函数的解析式为y=﹣x2+3x+4.
(2)①延长NQ交x轴于点P,
∵BC平行于x轴,C(0,4)
∴B(3,4),NP⊥OA.
根据题意,经过t秒时,NB=t,OM=2t,
则CN=3﹣t,AM=4﹣2t.
∵∠BCA=∠MAQ=45°,
∴QN=CN=3﹣t,
∴PQ=NP﹣NQ=4﹣(3﹣t)=1+t,
∴
=﹣t2+t+2.
∴.
∵a=﹣1<0,且0≤t≤2,∴S有最大值.
当t=时,S最大值=.
②存在点M,使得△AQM为直角三角形.
设经过t秒时,NB=t,OM=2t,
则CN=3﹣t,AM=4﹣2t,
∴∵∠BCA=∠MAQ=45°.
Ⅰ.若∠AQM=90°,
则PQ是等腰Rt△MQA底边MA上的高.
∴PQ是底边MA的中线,
∴PQ=AP=MA,
∴1+t=(4﹣2t),
解得,t=,
∴M的坐标为(1,0).
Ⅱ.若∠QMA=90°,此时QM与QP重合.
∴QM=QP=MA,
∴1+t=4﹣2t,
∴t=1,
∴点M的坐标为(2,0).
所以,使得△AQM为直角三角形的点M的坐标分别为(1,0)和(2,0).
4.解:(1)当 x=0 时,y=﹣2x﹣6=﹣6,则 C(0,﹣6),
当 y=0 时,﹣2x﹣6=0,
解得 x=﹣3,则 A(﹣3,0),
把 A(﹣3,0),C(0,﹣6)代入y=ax2+4x+c,得,
解得:,
∴抛物线解析式为y=2x2+4x﹣6;
(2)如图1,过点P作x轴的垂线与AC交于点H.
设点P的横坐标为m,
由直线AC:y=﹣2x﹣6,可得H(m,﹣2m﹣6).
又因为P(m,2m2+4m﹣6),所以HP=﹣2m2﹣6m.
因为△PAH 与△PCH 有公共底边HP,高的和为A、C 两点间的水平距离3,
所以S=S△APC=S△APH+S△CPH=(﹣2m2﹣6m)=﹣3(m+)2+,
∴当m=﹣时,S取得最大值,最大值为;
(3)如图2,过点P作PD⊥y轴于点D,设OQ=m,
则∠AOQ=∠PDQ=90°,
∵y=2x2+4x﹣6=2(x+1)2﹣8,
∴P(﹣1,﹣8),
则OD=8,PD=1,QD=8﹣m,
∵A(﹣3,0),
∴OA=3,
∵∠AQP=90°,
∴∠AQO+∠PQD=90°,
∵∠AQO+∠QAO=90°,
∴∠QAO=∠PQD,
∴△AOQ∽△QDP,
∴=,即=,
解得:m=4±,
∴点Q的坐标为(0,﹣4+)或(0,﹣4﹣).
5.解:(1)∵抛物线y=+bx+c,经过点A(1,3)、B(0,1),
∴ 解得:,c=1
∴抛物线的表达式为:
∵,
∴顶点坐标为:;
(2)∵A(1,3),∴把y=3代入,可得x1=1,x,2=4
∴C(4,3)
由B(0,1)、C(4,3)
得直线BC的表达式为,BC=
延长CA与y轴交于点I,则I(0,3)
∵点G是BC上方抛物线上的一个动点,分别过点G作GH⊥BC于点H、作GE⊥x轴于点E,交BC于点F,
∴△BCI∽△FGH
∴∠BCI=∠FGH
∵tan∠BCI===,
∴tan∠FGH=
设,则
∴GF===
∴当x=2时,GF最长,此时△GFH周长最大.
∴GF=2
∵
∴==
∴GH=
△GFH的周长为:GF+FH+GH=2++=+2;
(3)如图2,由题意,设N(1,n)
∵B(0,1)、C(4,3)
∴BN2=12+(n﹣1)2=n2﹣2n+2,
CN2=32+(n﹣3)2=n2﹣6n+18,
BC2=42+22=20
当∠BNC=90°时,BN2+CN2=BC2,即(n2﹣2n+2)+(n2﹣6n+18)=20
得n1=0,n2=4;
当∠CBN=90°时,BN2+BC2=CN2,即(n2﹣2n+2)+20=n2﹣6n+18
得n3=﹣1
当∠BCN=90°时,BC2+CN2=BN2,即20+n2﹣6n+18=n2﹣2n+2
得n4=9
综上所述:N点的坐标为:(1,0)或(1,4)或(1,﹣1)或(1,9)
6.解:(1)将点(﹣1,0),B(4,0)代入y=ax2+bx+2,
∴a=﹣,b=,
∴y=﹣x2+x+2;
(2)C(0,2),
∴BC的直线解析式为y=﹣x+2,
当t=时,AM=3,
∵AB=5,
∴MB=2,
∴M(2,0),N(2,1),D(2,3),
∴△DNB的面积=△DMB的面积﹣△MNB的面积=MB×DM﹣MB×MN=×2×2=2;
(3)∵BM=5﹣2t,
∴M(2t﹣1,0),
设P(2t﹣1,m),
∵PC2=(2t﹣1)2+(m﹣2)2,PB2=(2t﹣5)2+m2,
∵PB=PC,
∴(2t﹣1)2+(m﹣2)2=(2t﹣5)2+m2,
∴m=4t﹣5,
∴P(2t﹣1,4t﹣5),
∵PC⊥PB,
∴?=﹣1
∴t=1或t=2,
∴M(1,0)或M(3,0),
∴D(1,3)或D(3,2);
(4)当t=时,M(,0),
∴点Q在抛物线对称轴x=上,
如图:过点A作AC的垂线,以M为圆心AB为直径构造圆,圆与x=的交点分别为Q1与Q2,
∵AB=5,
∴AM=,
∵∠AQ1C+∠OAC=90°,∠OAC+∠MAG=90°,
∴∠AQ1C=∠MAG,
又∵∠AQ1C=∠CGA=∠MAG,
∴Q1(,﹣),
∵Q1与Q2关于x轴对称,
∴Q2(,),
∴Q点坐标分别为(,﹣),(,);
7.解:(1)将A(0,3),B(3,0),C(1,0)代入y=ax2+bx+c,得:
,解得:,
∴抛物线的解析式为y=x2﹣4x+3.
(2)设点P的坐标为(m,m2﹣4m+3).
∵点A的坐标为(0,3),点B的坐标为(3,0),
∴AP2=(m﹣0)2+(m2﹣4m+3﹣3)2=m4﹣8m3+17m2,BP2=(m﹣3)2+(m2﹣4m+3)2=m4﹣8m3+23m2﹣30m+18,AB2=(3﹣0)2+(0﹣3)2=18.
分两种情况考虑:
①当∠BAP=90°时,AB2+AP2=BP2,即18+m4﹣8m3+17m2=m4﹣8m3+23m2﹣30m+18,
整理,得:m2﹣5m=0,
解得:m1=0(舍去),m2=5,
∴点P的坐标为(5,8);
②当∠ABP=90°时,AB2+BP2=AP2,即18+m4﹣8m3+23m2﹣30m+18=m4﹣8m3+17m2,
整理,得:m2﹣5m+6=0,
解得:m3=2,m3=3(舍去),
∴点P的坐标为(2,﹣1).
综上所述:当△PAB是以AB为一直角边的直角三角形时,点P的坐标为(5,8)或(2,﹣1).
(3)存在,如图过点P作PD∥y轴交直线AB于点D.
设直线AB的解析式为y=kx+d(k≠0),
将A(0,3),B(3,0)代入y=kx+d,得:
,解得:,
∴直线AB的解析式为y=﹣x+3.
设点P的坐标为(n,n2﹣4n+3)(0<n<3),则点D的坐标为(n,﹣n+3),
∴PD=(﹣n+3)﹣(n2﹣4n+3)=﹣n2+3n,
∴S△PAB=OB?PD=﹣n2+n=﹣(n﹣)2+.
∵﹣<0,
∴当n=时,S△PAB取得最大值,此时最大值为,
∴当△PAB的面积取最大值时,点P的坐标为(,﹣).
8.解:(1)把B(3,0),C(0,3)代入y=x2+bx+c得:
,解得,
∴抛物线的解析式为y=x2﹣4x+3;
(2)①如图,抛物线的对称轴为直线x=﹣=2,
设D(2,y),则BC2=32+32=18,DC2=4+(y﹣3)2,BD2=(3﹣2)2+y2=1+y2,
当△BCD是以BC为直角边,BD为斜边的直角三角形时,
BC2+DC2=BD2,即18+4+(y﹣3)2=1+y2,
解得y=5,
此时D点坐标为(2,5);
当△BCD是以BC为直角边,CD为斜边的直角三角形时,
BC2+DB2=DC2,即4+(y﹣3)2=1+y2+18,
解得y=﹣1,
此时D点坐标为(2,﹣1);
②当△BCD是以BC为斜边的直角三角形时,
DC2+DB2=BC2,即4+(y﹣3)2+1+y2=18,
解得y1=,y2=,
此时D点坐标为(2,)或(2,),
所以△BCD是锐角三角形,点D的纵坐标的取值范围为<y<5或﹣1<y<.
9.解:(1)设抛物线的解析式为y=ax2+bx+c(a≠0).
将A(﹣1,0),B(3,0),C(0,3)代入y=ax2+bx+c,得:
,解得:,
∴抛物线的解析式为y=﹣x2+2x+3.
(2)在Rt△AOC中,OA=1,OC=3,
∴AC==.
∵AC′=AC,点A的坐标为(﹣1,0),
∴点C′的坐标为(﹣1,0).
在图1中,连接CC′,交AD于点D′,
∵点C,C′关于AD对称,
∴点D′的坐标为(,).
设直线AD的解析式为y=kx+d(k≠0),
将A(﹣1,0),D′(,)代入y=kx+d,得:
,解得:,
∴直线AD的解析式为y=x+.
当x=0时,y=x+=,
∴点E的坐标为(0,).
(3)在图2中,过点C′P⊥x轴,垂足为P.
∵FG∥AC,FG⊥AC′,
∴AC⊥AC′,
∴∠CAC′=90°.
∵∠CAO+∠C′AP=90°,∠CAO+∠ACO=90°,
∴∠C′AP=∠ACO.
在△CAO和△AC′P中,,
∴△CAO≌△AC′P(AAS),
∴AP=CO=3,C′P=AO=1,
∴点C′的坐标为(2,﹣1).
同(2)可求出直线AD的解析式为y=x+.
∵点A的坐标为(﹣1,0),点B的坐标为(3,0),点C的坐标为(0,3),
∴直线AC的解析式为y=3x+3,直线BC的解析式为y=﹣x+3.
联立直线AD及直线BC的解析式成方程组,得:,
解得:,
∴点F的坐标为(,).
∵直线FG∥AC,
∴设直线FG的解析式为y=3x+m.
将F(,)代入y=3x+m,得:=×3+m,
解得:m=﹣,
∴直线FG的解析式为y=3x﹣.
当y=0时,3x﹣=0,
解得:x=,
∴点M的横坐标为.
10.解:(1)由题意得:函数的对称轴为:x=2,则函数与x轴的另外一个交点坐标为(﹣2,0),
则函数的表达式为:y=a(x+2)(x﹣6)=a(x2﹣4x﹣12),
则﹣12a=4,解得:a=﹣,
故抛物线的表达式为:y=﹣x2+x+4;
(2)将点A、D的坐标代入一次函数表达式并解得:
直线AD的表达式为:y=﹣x+4,
则点E、F的坐标分别为:(t,4)、(t,0),
则点H(t,4﹣t),则点G(,4﹣t),
将点G的坐标代入表达式得:4﹣t=﹣()2+()+4,
解得:t=;
(3)点M(t+4,0),点E(t,4)、点F(t,0),
①当0<t≤2时,设EF交AD于点N(t,4﹣t),
S=S△EFM﹣S△FND=8﹣×(4﹣t)2=﹣t2+4t,
②2<t≤4时,
设直线EM交BC于点R,EF交AD于点K(t,4﹣t),
同理可得:直线ME的表达式为:y=﹣x+t+4,
直线BC的表达式为:y=﹣2x+12,
联立上述两式并解得:x=8﹣t,
故点R(8﹣t,2t﹣4),
S=S△EFM﹣S△RCM﹣S△KFD=4×4﹣(t+4﹣6)(2t﹣4)﹣×(4﹣t)2=﹣t2+8t﹣4;
③4<t≤6时,
同理可得:S=(6﹣t)(6﹣t)×2=t2﹣12t+36;
故S=
11.解:(1)抛物线的表达式为:y=a(x+3)(x﹣1)=a(x2+2x﹣3)=ax2+2ax﹣3a,
即﹣3a=2,解得:a=﹣,
故抛物线的表达式为:y=﹣x2﹣x+2,
(2)连接OP,设点P(x,﹣x2﹣x+2),
则S=S四边形ADCP=S△APO+S△CPO﹣S△ODC=×AO×yP+×OC×|xP|﹣×CO×OD
=(﹣x2﹣x+2)×2×(﹣x)﹣=﹣x2﹣3x+2,
∵﹣1<0,故S有最大值,当x=﹣时,S的最大值为;
(3)存在,理由:
△MNO为等腰直角三角形,且∠MNO为直角时,点N的位置如下图所示:
①当点N在x轴上方时,点N的位置为N1、N2,
N1的情况(△M1N1O):
设点N1的坐标为(x,﹣x2﹣x+2),则M1E=x+1,
过点N1作x轴的垂线交x轴于点F,过点M1作x轴的平行线交N1F于点E,
∵∠FN1O+∠M1N1E=90°,∠M1N1E+∠EM1N1=90°,∴∠EM1N1=∠FN1O,
∠M1EN1=∠N1FO=90°,ON1=M1N1,
∴△M1N1E≌△N1OF(AAS),∴M1E=N1F,
即:x+1=﹣x2﹣x+2,解得:x=(舍去负值),
则点N1(,);
N2的情况(△M2N2O):
同理可得:点N2(,);
②当点N在x轴下方时,点N的位置为N3、N4,
同理可得:点N3、N4的坐标分别为:(,)、(,).
综上,点N的坐标为:(,)或(,)或(,)或(,).
12.解:(1)抛物线y=ax2+bx+c的图象经过点B(1,0),其对称轴为直线l:x=2,则与x轴另外一个交点坐标为(3,0),
则抛物线的表达式为:y=a(x﹣1)(x﹣3)=a(x2﹣4x+3),
即3a=3,解得a=1,
故抛物线的表达式为:y=x2﹣4x+3;
∠AOB的平分线交线段AC于点E,则OE=OA=3,故点E(3,3),
四边形AOPE面积=△AOE的面积+△OPE的面积,由于△AOE的面积是定值,
故四边形AOPE面积最大,只需要确定△OPE的面积最大即可,
过点P作y轴的平行线交OE于点H,设点P(m,m2﹣4m+3),则点H(m,m),
S△OPE=×PH×AE=×(m﹣m2+4m﹣3)=﹣(m2﹣5m+3),
∵﹣<0,故△OPE的面积有最大值,即四边形AOPE面积最大,此时,m=,
故点P(P′)(,﹣),
连接AP′交抛物线对称轴于点M,则点M为所求,
将点AP′的坐标代入一次函数表达式并解得:
直线AP′的表达式为:y=﹣x+3,
当x=2时,y=0,即点M(2,0);
(2)当点P在一、四象限时,如下图,
过点P作x轴的平行线分别交y轴和直线l于点R、S,
设:RP=a,PS=b,则a+b=2,
∵∠OPR+∠ROP=90°,∠OPR+∠FPS=90°,∴∠FPS=∠ROP,
∠PKO=∠FSP=90°,PO=PF,∴△PKO≌△FSP(AAS),
则FS=RP=a,OR=PS,
故点P(a,a﹣2),
将点P的坐标代入抛物线表达式并解得:x=,
故点P的坐标为:(,)或(,);
当点P在第二象限时,
同理可设:点P(2﹣m,m),
同理可得点P(,)(舍去);
综上,点P的坐标为:(,)或(,).
13.解:(1)解:当x=0时,y=4,∴C(0,4)当y=0时,x=﹣4,∴A(﹣4,0),
∵OC=2OB,∴OB=2,B(2,0),
将点A、B、C的坐标代入抛物线解析式得,
解得:,
∴抛物线的解析式为;
(2)过点D作DE⊥x轴于E,作QF⊥DE于F,
∴四边形QOEF为矩形,
∴QF=OE,QO=FE,设QF=m,
∵△QDF≌△DPE,
∴QF=DE=m,FD=EP,
∵FD=4+t﹣m,EP=4﹣t+m,
∴4﹣t+m=4+t﹣m,∴m=t,
∵OP=4﹣t,
∴(0<t<4);
(3)作PL∥OQ交AC于点L,作GM⊥AB于M,KN⊥AB于N,
∵OC=OA,∴PL=PA∵PA=CQ∴PL=CQ,
∴△PGL≌△QGC,∴GP=GQ,
∵OG=,∴PQ=,
在△OPQ中,由勾股定理得:(4﹣t)2+(4+t)2=,
∴t=2;
∵△PDG为等腰直角三角形,∴四边形PGDK为正方形,
∵OQ=6∴GM=3
∵GP=GO∴PM=MO=1,
∵△GMP≌△PNK(AAS),
∴GM=PN=3,PM=KN=1,
∴AN=5,ON=1,
∴K(1,﹣1)
与直角三角形相关的压轴题(附答案)
方法提炼(1):
1、利用坐标系中两点距离公式,得到所求三角形三边平方的代数式;
2、确定三角形中的直角顶点,若无法确定则分情况讨论;
3、根据勾股定理得到方程,然后解方程,若方程有解,此点存在;否则不存在;
方法提炼(2):
1、利用两直线垂直,K值互为负倒数(K1K2=-1),先确定点所在的直线表达式
2、将直线与抛物线的表达式联立方程组,若求出交点坐标,此点存在;否则不存在;
方法提炼(3):
1、利用特殊角45°构造直角三角形,易求点的坐标。
典例引领:
3.如图,抛物线y=﹣x2+bx+c经过A(4,0),B(0,4)两点,C为OA的中点,连接BC.
(1)求抛物线的解析式;
(2)P为第一象限抛物线上一点,连接PB,PC,当△PBC的面积为6时,求点P的坐标;
(3)M在线段BC上,在坐标平面内,以BM为直角边作等腰直角△BMN,当点N在抛物线上时,直接写出点M的坐标.
分析:(1)利用待定系数法求抛物线的解析式;
(2)作PQ∥y轴交直线BC于Q,如图1,先确定直线BC的解析式为y=﹣2x+4;设P(x,﹣x2+3x+4),则Q(x,﹣2x+4),所以PQ=﹣x2+5x,利用三角形面积公式得到S△PBC=S△PQB﹣S△PCQ=PQ,则﹣x2+5x=6,然后解方程求出x即可得到P点坐标;
(3)设M(t,﹣2t+4)(0<t≤2),当∠BMN=90°时,作ME⊥y轴于E,NF⊥EM于F,如图2,先证明△BME≌MNF得到ME=NF=t,BE=MF=2t,则N(3t,﹣t+4),接着把N(3t,﹣t+4)代入y=﹣x2+3x+4得﹣(3t)2+9t+4=﹣t+4;然后表示出点N关于点M的对称点N′的坐标为(﹣t,﹣3t+4),把N′(﹣t,﹣3t+4)代入y=﹣x2+3x+4得﹣(﹣t)2﹣3t+4=﹣3t+4;当∠MBN=90°时,作ME⊥y轴于E,NF⊥y轴于F,如图3,通过证明△BME≌NBF得到ME=BF=t,BE=NF=2t,则N(2t,t+4),然后把N(2t,t+4)代入y=﹣x2+3x+4得﹣(2t)2+6t+4=t+4,最后分别解关于t的方程可得到满足条件的M点坐标.
解:(1)解:根据题意得,解得:b=3,c=4,
抛物线的解析式为y=﹣x2+3x+4;
(2)∵C为OA的中点,
∴C点坐标是(2,0)
作PQ∥y轴交直线BC于Q,如图1,
设直线BC的解析式为y=mx+n,
把B(0,4),C(2,0)代入得,解得,
∴直线BC的解析式为y=﹣2x+4;
设P(x,﹣x2+3x+4),则Q(x,﹣2x+4),
∴PQ=﹣x2+3x+4﹣(﹣2x+4)=﹣x2+5x,
∵S△PBC=S△PQB﹣S△PCQ=PQ?2=PQ,
∴﹣x2+5x=6,
整理得x2﹣5x+6=0,解得x1=3,x2=2,
∴P点坐标为(3,4)或(2,6);
(3)设M(t,﹣2t+4)(0<t≤2),
当∠BMN=90°时,作ME⊥y轴于E,NF⊥EM于F,如图2,
∵△BMN为等腰直角三角形,
∴BM=MN,
易得△BME≌MNF(AAS),则ME=NF=t,BE=MF=4﹣(﹣2t+4)=2t,
∴N(3t,﹣t+4),
把N(3t,﹣t+4)代入y=﹣x2+3x+4得﹣(3t)2+9t+4=﹣t+4,解得t1=0(舍去),t2=,此时M点坐标为(,);
点N(3t,﹣t+4)关于点M(t,﹣2t+4)的对称点N′的坐标为(﹣t,﹣3t+4),
把N′(﹣t,﹣3t+4)代入y=﹣x2+3x+4得﹣(﹣t)2﹣3t+4=﹣3t+4,解得t1=t2=0(舍去);
当∠MBN=90°时,作ME⊥y轴于E,NF⊥y轴于F,如图3,
∵△BMN为等腰直角三角形,
∴BM=BN,
易得△BME≌NBF(AAS),则ME=BF=t,BE=NF=4﹣(﹣2t+4)=2t,
∴N(2t,t+4),
把N(2t,t+4)代入y=﹣x2+3x+4得﹣(2t)2+6t+4=t+4,解得t1=0(舍去),t2=,此时M点坐标为(,);
综上所述,M点坐标为(,)或(,).
点评:本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质和等腰直角三角形的性质;会利用待定系数法求函数解析式;理解坐标与图形性质;会运用分类讨论的思想解决数学问题.
跟踪训练:
1.如图,在平面直角坐标系中抛物线与x轴交于点A(﹣1,0),B(3,0),与y轴交于点C(0,3),与直线l:y=k(x﹣3)+3(k>0)交于D,E两点.
(1)求抛物线的解析式;
(2)连接BD,BE,若△BDE的面积为6,求k的值;
(3)点P为直线DE上的一点,若△PAB为直角三角形,且满足条件的点P有且只有3个,直接写出k的值为 .
2.如图1,二次函数y=ax2+bx﹣2(a≠0)的图象与x轴交于A(﹣4,0)、B(1,0)两点,与y轴交于点C.
(1)求这个二次函数的表达式:
(2)点M在该抛物线的对称轴上,当△ACM是直角三角形时,求点M的坐标;
(3)如图2,点D在y轴上,且CD=OA,连接AD,点E、F分别是线段OA,AD上的动点,求EF+OF的最小值.
3.如图,已知二次函数y=ax2+bx+4的图象与x轴交于点A(4,0)和点D(﹣1,0),与y轴交于点C,过点C作BC平行于x轴交抛物线于点B,连接AC
(1)求这个二次函数的表达式;
(2)点M从点O出发以每秒2个单位长度的速度向点A运动;点N从点B同时出发,以每秒1个单位长度的速度向点C运动,其中一个动点到达终点时,另一个动点也随之停动,过点N作NQ垂直于BC交AC于点Q,连结MQ
①求△AQM的面积S与运动时间t之间的函数关系式,写出自变量的取值范围;当t为何值时,S有最大值,并求出S的最大值;
②是否存在点M,使得△AQM为直角三角形?若存在,求出点M的坐标;若不存在,说明理由.
4.如图,二次函数y=ax2+4x+c(a≠0)的图象与x轴交A,B两点,与y轴交于点C,直线y=﹣2x﹣6经过点A,C.
(1)求该二次函数的解析式;
(2)点P为第三象限内抛物线上的一个动点,△APC的面积为S,试求S的最大值;
(3)若P为抛物线的顶点,且直角三角形APQ的直角顶点Q在y轴上,请直接写出点Q的坐标.
5.在平面直角坐标系中,抛物线y=+bx+c,经过点A(1,3)、B(0,1),过点A作x轴的平行线交抛物线于另一点C
(1)求抛物线的表达式及其顶点坐标;
(2)如图1,点G是BC上方抛物线上的一个动点,分别过点G作GH⊥BC于点H、作GE⊥x轴于点E,交BC于点F,在点G运动的过程中,△GFH的周长是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由;
(3)如图2,过A点的直线垂直x轴于点M,点N为直线AM上任意一点,当△BCN为直角三角形时,请直接写出点N的坐标.
6.二次函数y=ax2+bx+2的图象交x轴于点(﹣1,0),B(4,0)两点,交y轴于点C.动点M从点A出发,以每秒2个单位长度的速度沿AB方向运动,过点M作MN⊥x轴交直线BC于点N,交抛物线于点D,连接AC,设运动的时间为t秒.
(1)求二次函数y=ax2+bx+2的表达式;
(2)连接BD,当t=时,求△DNB的面积;
(3)在直线MN上存在一点P,当△PBC是以∠BPC为直角的等腰直角三角形时,求此时点D的坐标;
(4)当t=时,在直线MN上存在一点Q,使得∠AQC+∠OAC=90°,求点Q的坐标.
7.如图A(0,3),B(3,0),C(1,0)分别是抛物线:y=ax2+bx+c(a≠0)上的三点,点P为抛物线上一动点.
(1)求此抛物线的解析式.
(2)当△PAB是以AB为一直角边的直角三角形时,求此时点P的坐标.
(3)若点P在抛物线上A、B两点之间移动时,是否存在一个位置,使△PAB的面积最大?若存在,请求此时点P的坐标.若不存在,请说明理由.
8.如图,抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,3).
(1)求抛物线对应函数的关系式,及A点坐标.
(2)点D为抛物线对称轴上一点.
①当△BCD是以BC为直角边的直角三角形时,求点D的坐标;
②若△BCD是锐角三角形,求点D的纵坐标的取值范围.
9.已知抛物线经过点A(﹣1,0)、点B(3,0)、点C(0,3),点D为抛物线在第一象限内图象上一动点,连接AD,交y轴于点E,将点C关于线段AD作轴对称,对称点为C',连接AC'.
(1)求抛物线的解析式;
(2)如图1如果点C'落在x轴,求点E坐标;
(3)如图2,连接AC、BC,BC与AD交于点F,拖动点D,点C'落在第四象限,作FG∥AC,交x轴于点M,交AC'于点G,若∠AGF=90°,求点M的横坐标.
10.如图,抛物线y=ax2+bx+4交y轴于点A,并经过B(4,4)和C(6,0)两点,点D的坐标为(4,0),连接AD,BC,点F从点O出发,以每秒1个单位长度的速度沿线段OC方向运动,到达点C后停止运动:点M同时从点D出发以每秒1个单位长度的速度沿x轴正方向运动,当点F停止时点M也停止运动.设点F的运动时间为t秒,过点F作AB的垂线EF交直线AB于点E,交AD于点H.
(1)求抛物线的解析式;
(2)以线段EH为斜边向右作等腰直角△EHG,当点G落在第一象限内的抛物线上时,求出t的值;
(3)设△EFM与四边形ADCB重合时的面积为S,请直接写出S与t的函数关系式与相应的自变量t的取值范围.
11.如图,抛物线y=ax2+bx+2交x轴于点A(﹣3,0)和点B(1,0),交y轴于点C.
(1)求这个抛物线的函数表达式.
(2)点D的坐标为(﹣1,0),点P为第二象限内抛物线上的一个动点,求四边形ADCP面积的最大值.
(3)点M为抛物线对称轴上的点,问:在抛物线上是否存在点N,使△MNO为等腰直角三角形,且∠MNO为直角?若存在,请直接写出点N的坐标;若不存在,请说明理由.
12.如图①,已知抛物线y=ax2+bx+c的图象经过点A(0,3)、B(1,0),其对称轴为直线l:x=2,过点A作AC∥x轴交抛物线于点C,∠AOB的平分线交线段AC于点E,点P是抛物线上的一个动点,设其横坐标为m.
(1)若动点P在直线OE下方的抛物线上,连结PE、PO,当m为何值时,四边形AOPE面积最大?当四边形AOPE面积最大时,在抛物线对称轴直线上找一点M,使得MB+MP的值最小,求M的坐标;
(2)如图②,F是抛物线的对称轴l上的一点,在抛物线上是否存在点P使△POF成为以点P为直角顶点的等腰直角三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
13.已知直线y=x+4与x轴、y轴分别交于A、C两点,抛物线y=ax2+bx+c经过A、C两点,与x轴的另一个交点为B,且OC=2OB.
(1)求抛物线的解析式;
(2)点P在AO上,点Q在OC的延长线上,且AP=CQ,连接PQ交AC于点G,点D为第一象限内的一点,当△PDQ是以PQ为斜边的等腰直角三角形时,连接OD,设AP的长度为t,△POD的面积为S,请用含t的式子表示S,并写出自变量t的取值范围;
(3)在(2)的条件下,连接OG、DG,将△PGD沿PD翻折到PDK的位置(G与K对应),若OG=,求点K的坐标.
参考答案
1.解:(1)∵抛物线与x轴交于点A(﹣1,0),B(3,0),
∴设解析式为y=a(x+1)(x﹣3)
∵抛物线交y轴于点C(0,3)
∴﹣3a=3
∴a=﹣1
∴抛物线的解析式为y=﹣(x+1)(x﹣3)=﹣x2+2x+3
(2)直线l:y=k(x﹣3)+3,当x=3时,y=3
∴直线l过定点F(3,3)
如图1,连接BF,则BF⊥x轴,BF=3
设点D横坐标为x1,点E横坐标为x2,
∵ 整理得:x2+(k﹣2)x﹣3k=0
∴x1+x2=2﹣k,x1x2=﹣3k
∵S△BDE=S△BDF﹣S△BEF=BF?(3﹣x1)﹣BF?(3﹣x2)=BF?(x2﹣x1)=6
∴x2﹣x1=4
∵(x1+x2)2﹣4x1x2=(x2﹣x1)2
∴(2﹣k)2﹣4(﹣3k)=16
解得:k1=﹣﹣4(舍去) k2=﹣4
∴k的值为
(3)∵△PAB为直角三角形,且在直线DE上各有一个点P满足∠PAB=90°与∠PBA=90°
∴只有1个点P满足∠APB=90°
∴直线DE与以AB为直径的圆相切
如图2,取AB中点G(1,0),G为圆心,PG=BG=2
设P(p,kp﹣3k+3),
∴PG2=(p﹣1)2+(kp﹣3k+3)2=4
整理得:(k2+1)p2+(6k﹣6k2﹣2)p+9k2﹣18k+6=0
∵有一个且只有一个满足条件的点P
∴△=(6k﹣6k2﹣2)2﹣4(k2+1)(9k2﹣18k+6)=0
解得:k=
故答案为:
2.解:(1)将A(﹣4,0)、B(1,0)的坐标分别代入y=ax2+bx﹣2,得
,
解得,,
∴这个二次函数的函数表达式为y=x2+x﹣2.
(2)由x=0得y=﹣2,
∴C(0,﹣2).
抛物线的对称轴为直线x=,即直线x=﹣,
设点M的坐标为(﹣,m),
AM2=(﹣+4)2+m2=+m2,CM2=()2+(m+2)2=+(m+2)2,AC2=42+22=20,
①当∠CAM=90°时,AM2+AC2=CM2,
即+m2+20=+(m+2)2,
解得m=5,
∴M(﹣,5),
②当∠ACM=90°时,AC2+CM2=AM2,即20++(m+2)2=+m2.解得m=﹣5,
∴M(﹣,﹣5),
③当∠AMC=90°时,AM2+CM2=AC2,即+m2++(m+2)2=20,
解得m1=,m2=,
∴M(﹣,)或(﹣,).
综上可知:点M的坐标为(﹣,5)、(﹣,﹣5)、(﹣,)或(﹣,).
(3)如图,作点O关于直线AD的对称点O′,过O′作O′H⊥OA于点H,则EF+OF的最小值为线段O′H的长.
连接OO′交AD于点M,则OO′⊥AD,且M是线段OO′的中点,
∵CD=OA=4,OC=2,
∴OD=2,
即点D的坐标为(0,2),
在Rt△AOD中,AD=,
∴sin∠DAO=,
∴OM=OA?sin∠DAO=4×=,
∴OO′=,
∴OH=OO′?sin∠OO′H=OO′?sin∠DAO=?=,
∴O′H=,
∴点O′(﹣,),
∴EF+OF的最小值=O′H=.
3.解:(1)∵二次函数的图象经过A(4,0)和点D(﹣1,0),
∴,
解得,
所以,二次函数的解析式为y=﹣x2+3x+4.
(2)①延长NQ交x轴于点P,
∵BC平行于x轴,C(0,4)
∴B(3,4),NP⊥OA.
根据题意,经过t秒时,NB=t,OM=2t,
则CN=3﹣t,AM=4﹣2t.
∵∠BCA=∠MAQ=45°,
∴QN=CN=3﹣t,
∴PQ=NP﹣NQ=4﹣(3﹣t)=1+t,
∴
=﹣t2+t+2.
∴.
∵a=﹣1<0,且0≤t≤2,∴S有最大值.
当t=时,S最大值=.
②存在点M,使得△AQM为直角三角形.
设经过t秒时,NB=t,OM=2t,
则CN=3﹣t,AM=4﹣2t,
∴∵∠BCA=∠MAQ=45°.
Ⅰ.若∠AQM=90°,
则PQ是等腰Rt△MQA底边MA上的高.
∴PQ是底边MA的中线,
∴PQ=AP=MA,
∴1+t=(4﹣2t),
解得,t=,
∴M的坐标为(1,0).
Ⅱ.若∠QMA=90°,此时QM与QP重合.
∴QM=QP=MA,
∴1+t=4﹣2t,
∴t=1,
∴点M的坐标为(2,0).
所以,使得△AQM为直角三角形的点M的坐标分别为(1,0)和(2,0).
4.解:(1)当 x=0 时,y=﹣2x﹣6=﹣6,则 C(0,﹣6),
当 y=0 时,﹣2x﹣6=0,
解得 x=﹣3,则 A(﹣3,0),
把 A(﹣3,0),C(0,﹣6)代入y=ax2+4x+c,得,
解得:,
∴抛物线解析式为y=2x2+4x﹣6;
(2)如图1,过点P作x轴的垂线与AC交于点H.
设点P的横坐标为m,
由直线AC:y=﹣2x﹣6,可得H(m,﹣2m﹣6).
又因为P(m,2m2+4m﹣6),所以HP=﹣2m2﹣6m.
因为△PAH 与△PCH 有公共底边HP,高的和为A、C 两点间的水平距离3,
所以S=S△APC=S△APH+S△CPH=(﹣2m2﹣6m)=﹣3(m+)2+,
∴当m=﹣时,S取得最大值,最大值为;
(3)如图2,过点P作PD⊥y轴于点D,设OQ=m,
则∠AOQ=∠PDQ=90°,
∵y=2x2+4x﹣6=2(x+1)2﹣8,
∴P(﹣1,﹣8),
则OD=8,PD=1,QD=8﹣m,
∵A(﹣3,0),
∴OA=3,
∵∠AQP=90°,
∴∠AQO+∠PQD=90°,
∵∠AQO+∠QAO=90°,
∴∠QAO=∠PQD,
∴△AOQ∽△QDP,
∴=,即=,
解得:m=4±,
∴点Q的坐标为(0,﹣4+)或(0,﹣4﹣).
5.解:(1)∵抛物线y=+bx+c,经过点A(1,3)、B(0,1),
∴ 解得:,c=1
∴抛物线的表达式为:
∵,
∴顶点坐标为:;
(2)∵A(1,3),∴把y=3代入,可得x1=1,x,2=4
∴C(4,3)
由B(0,1)、C(4,3)
得直线BC的表达式为,BC=
延长CA与y轴交于点I,则I(0,3)
∵点G是BC上方抛物线上的一个动点,分别过点G作GH⊥BC于点H、作GE⊥x轴于点E,交BC于点F,
∴△BCI∽△FGH
∴∠BCI=∠FGH
∵tan∠BCI===,
∴tan∠FGH=
设,则
∴GF===
∴当x=2时,GF最长,此时△GFH周长最大.
∴GF=2
∵
∴==
∴GH=
△GFH的周长为:GF+FH+GH=2++=+2;
(3)如图2,由题意,设N(1,n)
∵B(0,1)、C(4,3)
∴BN2=12+(n﹣1)2=n2﹣2n+2,
CN2=32+(n﹣3)2=n2﹣6n+18,
BC2=42+22=20
当∠BNC=90°时,BN2+CN2=BC2,即(n2﹣2n+2)+(n2﹣6n+18)=20
得n1=0,n2=4;
当∠CBN=90°时,BN2+BC2=CN2,即(n2﹣2n+2)+20=n2﹣6n+18
得n3=﹣1
当∠BCN=90°时,BC2+CN2=BN2,即20+n2﹣6n+18=n2﹣2n+2
得n4=9
综上所述:N点的坐标为:(1,0)或(1,4)或(1,﹣1)或(1,9)
6.解:(1)将点(﹣1,0),B(4,0)代入y=ax2+bx+2,
∴a=﹣,b=,
∴y=﹣x2+x+2;
(2)C(0,2),
∴BC的直线解析式为y=﹣x+2,
当t=时,AM=3,
∵AB=5,
∴MB=2,
∴M(2,0),N(2,1),D(2,3),
∴△DNB的面积=△DMB的面积﹣△MNB的面积=MB×DM﹣MB×MN=×2×2=2;
(3)∵BM=5﹣2t,
∴M(2t﹣1,0),
设P(2t﹣1,m),
∵PC2=(2t﹣1)2+(m﹣2)2,PB2=(2t﹣5)2+m2,
∵PB=PC,
∴(2t﹣1)2+(m﹣2)2=(2t﹣5)2+m2,
∴m=4t﹣5,
∴P(2t﹣1,4t﹣5),
∵PC⊥PB,
∴?=﹣1
∴t=1或t=2,
∴M(1,0)或M(3,0),
∴D(1,3)或D(3,2);
(4)当t=时,M(,0),
∴点Q在抛物线对称轴x=上,
如图:过点A作AC的垂线,以M为圆心AB为直径构造圆,圆与x=的交点分别为Q1与Q2,
∵AB=5,
∴AM=,
∵∠AQ1C+∠OAC=90°,∠OAC+∠MAG=90°,
∴∠AQ1C=∠MAG,
又∵∠AQ1C=∠CGA=∠MAG,
∴Q1(,﹣),
∵Q1与Q2关于x轴对称,
∴Q2(,),
∴Q点坐标分别为(,﹣),(,);
7.解:(1)将A(0,3),B(3,0),C(1,0)代入y=ax2+bx+c,得:
,解得:,
∴抛物线的解析式为y=x2﹣4x+3.
(2)设点P的坐标为(m,m2﹣4m+3).
∵点A的坐标为(0,3),点B的坐标为(3,0),
∴AP2=(m﹣0)2+(m2﹣4m+3﹣3)2=m4﹣8m3+17m2,BP2=(m﹣3)2+(m2﹣4m+3)2=m4﹣8m3+23m2﹣30m+18,AB2=(3﹣0)2+(0﹣3)2=18.
分两种情况考虑:
①当∠BAP=90°时,AB2+AP2=BP2,即18+m4﹣8m3+17m2=m4﹣8m3+23m2﹣30m+18,
整理,得:m2﹣5m=0,
解得:m1=0(舍去),m2=5,
∴点P的坐标为(5,8);
②当∠ABP=90°时,AB2+BP2=AP2,即18+m4﹣8m3+23m2﹣30m+18=m4﹣8m3+17m2,
整理,得:m2﹣5m+6=0,
解得:m3=2,m3=3(舍去),
∴点P的坐标为(2,﹣1).
综上所述:当△PAB是以AB为一直角边的直角三角形时,点P的坐标为(5,8)或(2,﹣1).
(3)存在,如图过点P作PD∥y轴交直线AB于点D.
设直线AB的解析式为y=kx+d(k≠0),
将A(0,3),B(3,0)代入y=kx+d,得:
,解得:,
∴直线AB的解析式为y=﹣x+3.
设点P的坐标为(n,n2﹣4n+3)(0<n<3),则点D的坐标为(n,﹣n+3),
∴PD=(﹣n+3)﹣(n2﹣4n+3)=﹣n2+3n,
∴S△PAB=OB?PD=﹣n2+n=﹣(n﹣)2+.
∵﹣<0,
∴当n=时,S△PAB取得最大值,此时最大值为,
∴当△PAB的面积取最大值时,点P的坐标为(,﹣).
8.解:(1)把B(3,0),C(0,3)代入y=x2+bx+c得:
,解得,
∴抛物线的解析式为y=x2﹣4x+3;
(2)①如图,抛物线的对称轴为直线x=﹣=2,
设D(2,y),则BC2=32+32=18,DC2=4+(y﹣3)2,BD2=(3﹣2)2+y2=1+y2,
当△BCD是以BC为直角边,BD为斜边的直角三角形时,
BC2+DC2=BD2,即18+4+(y﹣3)2=1+y2,
解得y=5,
此时D点坐标为(2,5);
当△BCD是以BC为直角边,CD为斜边的直角三角形时,
BC2+DB2=DC2,即4+(y﹣3)2=1+y2+18,
解得y=﹣1,
此时D点坐标为(2,﹣1);
②当△BCD是以BC为斜边的直角三角形时,
DC2+DB2=BC2,即4+(y﹣3)2+1+y2=18,
解得y1=,y2=,
此时D点坐标为(2,)或(2,),
所以△BCD是锐角三角形,点D的纵坐标的取值范围为<y<5或﹣1<y<.
9.解:(1)设抛物线的解析式为y=ax2+bx+c(a≠0).
将A(﹣1,0),B(3,0),C(0,3)代入y=ax2+bx+c,得:
,解得:,
∴抛物线的解析式为y=﹣x2+2x+3.
(2)在Rt△AOC中,OA=1,OC=3,
∴AC==.
∵AC′=AC,点A的坐标为(﹣1,0),
∴点C′的坐标为(﹣1,0).
在图1中,连接CC′,交AD于点D′,
∵点C,C′关于AD对称,
∴点D′的坐标为(,).
设直线AD的解析式为y=kx+d(k≠0),
将A(﹣1,0),D′(,)代入y=kx+d,得:
,解得:,
∴直线AD的解析式为y=x+.
当x=0时,y=x+=,
∴点E的坐标为(0,).
(3)在图2中,过点C′P⊥x轴,垂足为P.
∵FG∥AC,FG⊥AC′,
∴AC⊥AC′,
∴∠CAC′=90°.
∵∠CAO+∠C′AP=90°,∠CAO+∠ACO=90°,
∴∠C′AP=∠ACO.
在△CAO和△AC′P中,,
∴△CAO≌△AC′P(AAS),
∴AP=CO=3,C′P=AO=1,
∴点C′的坐标为(2,﹣1).
同(2)可求出直线AD的解析式为y=x+.
∵点A的坐标为(﹣1,0),点B的坐标为(3,0),点C的坐标为(0,3),
∴直线AC的解析式为y=3x+3,直线BC的解析式为y=﹣x+3.
联立直线AD及直线BC的解析式成方程组,得:,
解得:,
∴点F的坐标为(,).
∵直线FG∥AC,
∴设直线FG的解析式为y=3x+m.
将F(,)代入y=3x+m,得:=×3+m,
解得:m=﹣,
∴直线FG的解析式为y=3x﹣.
当y=0时,3x﹣=0,
解得:x=,
∴点M的横坐标为.
10.解:(1)由题意得:函数的对称轴为:x=2,则函数与x轴的另外一个交点坐标为(﹣2,0),
则函数的表达式为:y=a(x+2)(x﹣6)=a(x2﹣4x﹣12),
则﹣12a=4,解得:a=﹣,
故抛物线的表达式为:y=﹣x2+x+4;
(2)将点A、D的坐标代入一次函数表达式并解得:
直线AD的表达式为:y=﹣x+4,
则点E、F的坐标分别为:(t,4)、(t,0),
则点H(t,4﹣t),则点G(,4﹣t),
将点G的坐标代入表达式得:4﹣t=﹣()2+()+4,
解得:t=;
(3)点M(t+4,0),点E(t,4)、点F(t,0),
①当0<t≤2时,设EF交AD于点N(t,4﹣t),
S=S△EFM﹣S△FND=8﹣×(4﹣t)2=﹣t2+4t,
②2<t≤4时,
设直线EM交BC于点R,EF交AD于点K(t,4﹣t),
同理可得:直线ME的表达式为:y=﹣x+t+4,
直线BC的表达式为:y=﹣2x+12,
联立上述两式并解得:x=8﹣t,
故点R(8﹣t,2t﹣4),
S=S△EFM﹣S△RCM﹣S△KFD=4×4﹣(t+4﹣6)(2t﹣4)﹣×(4﹣t)2=﹣t2+8t﹣4;
③4<t≤6时,
同理可得:S=(6﹣t)(6﹣t)×2=t2﹣12t+36;
故S=
11.解:(1)抛物线的表达式为:y=a(x+3)(x﹣1)=a(x2+2x﹣3)=ax2+2ax﹣3a,
即﹣3a=2,解得:a=﹣,
故抛物线的表达式为:y=﹣x2﹣x+2,
(2)连接OP,设点P(x,﹣x2﹣x+2),
则S=S四边形ADCP=S△APO+S△CPO﹣S△ODC=×AO×yP+×OC×|xP|﹣×CO×OD
=(﹣x2﹣x+2)×2×(﹣x)﹣=﹣x2﹣3x+2,
∵﹣1<0,故S有最大值,当x=﹣时,S的最大值为;
(3)存在,理由:
△MNO为等腰直角三角形,且∠MNO为直角时,点N的位置如下图所示:
①当点N在x轴上方时,点N的位置为N1、N2,
N1的情况(△M1N1O):
设点N1的坐标为(x,﹣x2﹣x+2),则M1E=x+1,
过点N1作x轴的垂线交x轴于点F,过点M1作x轴的平行线交N1F于点E,
∵∠FN1O+∠M1N1E=90°,∠M1N1E+∠EM1N1=90°,∴∠EM1N1=∠FN1O,
∠M1EN1=∠N1FO=90°,ON1=M1N1,
∴△M1N1E≌△N1OF(AAS),∴M1E=N1F,
即:x+1=﹣x2﹣x+2,解得:x=(舍去负值),
则点N1(,);
N2的情况(△M2N2O):
同理可得:点N2(,);
②当点N在x轴下方时,点N的位置为N3、N4,
同理可得:点N3、N4的坐标分别为:(,)、(,).
综上,点N的坐标为:(,)或(,)或(,)或(,).
12.解:(1)抛物线y=ax2+bx+c的图象经过点B(1,0),其对称轴为直线l:x=2,则与x轴另外一个交点坐标为(3,0),
则抛物线的表达式为:y=a(x﹣1)(x﹣3)=a(x2﹣4x+3),
即3a=3,解得a=1,
故抛物线的表达式为:y=x2﹣4x+3;
∠AOB的平分线交线段AC于点E,则OE=OA=3,故点E(3,3),
四边形AOPE面积=△AOE的面积+△OPE的面积,由于△AOE的面积是定值,
故四边形AOPE面积最大,只需要确定△OPE的面积最大即可,
过点P作y轴的平行线交OE于点H,设点P(m,m2﹣4m+3),则点H(m,m),
S△OPE=×PH×AE=×(m﹣m2+4m﹣3)=﹣(m2﹣5m+3),
∵﹣<0,故△OPE的面积有最大值,即四边形AOPE面积最大,此时,m=,
故点P(P′)(,﹣),
连接AP′交抛物线对称轴于点M,则点M为所求,
将点AP′的坐标代入一次函数表达式并解得:
直线AP′的表达式为:y=﹣x+3,
当x=2时,y=0,即点M(2,0);
(2)当点P在一、四象限时,如下图,
过点P作x轴的平行线分别交y轴和直线l于点R、S,
设:RP=a,PS=b,则a+b=2,
∵∠OPR+∠ROP=90°,∠OPR+∠FPS=90°,∴∠FPS=∠ROP,
∠PKO=∠FSP=90°,PO=PF,∴△PKO≌△FSP(AAS),
则FS=RP=a,OR=PS,
故点P(a,a﹣2),
将点P的坐标代入抛物线表达式并解得:x=,
故点P的坐标为:(,)或(,);
当点P在第二象限时,
同理可设:点P(2﹣m,m),
同理可得点P(,)(舍去);
综上,点P的坐标为:(,)或(,).
13.解:(1)解:当x=0时,y=4,∴C(0,4)当y=0时,x=﹣4,∴A(﹣4,0),
∵OC=2OB,∴OB=2,B(2,0),
将点A、B、C的坐标代入抛物线解析式得,
解得:,
∴抛物线的解析式为;
(2)过点D作DE⊥x轴于E,作QF⊥DE于F,
∴四边形QOEF为矩形,
∴QF=OE,QO=FE,设QF=m,
∵△QDF≌△DPE,
∴QF=DE=m,FD=EP,
∵FD=4+t﹣m,EP=4﹣t+m,
∴4﹣t+m=4+t﹣m,∴m=t,
∵OP=4﹣t,
∴(0<t<4);
(3)作PL∥OQ交AC于点L,作GM⊥AB于M,KN⊥AB于N,
∵OC=OA,∴PL=PA∵PA=CQ∴PL=CQ,
∴△PGL≌△QGC,∴GP=GQ,
∵OG=,∴PQ=,
在△OPQ中,由勾股定理得:(4﹣t)2+(4+t)2=,
∴t=2;
∵△PDG为等腰直角三角形,∴四边形PGDK为正方形,
∵OQ=6∴GM=3
∵GP=GO∴PM=MO=1,
∵△GMP≌△PNK(AAS),
∴GM=PN=3,PM=KN=1,
∴AN=5,ON=1,
∴K(1,﹣1)
同课章节目录
