2021年九年级中考数学复习《探索二次函数综合型压轴题解题技巧》分类训练四:与等腰三角形相关的压轴题(附答案)
文档属性
| 名称 | 2021年九年级中考数学复习《探索二次函数综合型压轴题解题技巧》分类训练四:与等腰三角形相关的压轴题(附答案) |  | |
| 格式 | doc | ||
| 文件大小 | 671.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-20 09:17:04 | ||
图片预览


文档简介
2021中考数学复习《探索二次函数综合型压轴题解题技巧》分类训练四:
与等腰三角形相关的压轴题(附答案)
方法提炼:
1、设出点坐标,利用等腰三角形的性质求边长;
2、当所给定长未说明是等腰三角形的底还是腰时,需分情况讨论:
①当定长为腰,找已知直线上满足条件的点时,以定长的某一端点为圆心,以定长为半径画弧,若所画弧与已知直线有交点且交点不是定长的另一端点时,交点即为所求的点;若所画弧与已知直线无交点或交点是定长的另一端点时,满足条件的点不存在;
②当定长为底边时,作出定长的垂直平分线,若作出的垂直平分线与已知直线有交点,则交点即为所求的点,若作出的垂直平分线与已知直线无交点,则满足条件的点不存在.用以上方法即可找出所有符合条件的点。
典例引领:
例:如图,直线y=3x+3交x轴于点A,交y轴于点B,过A、B两点的抛物线交x轴于另一点C(3,0)。
(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在点Q,使△ABQ是等腰三角形?若存在,求出符合条件的点Q的坐标;若不存在,请说明理由。
解:(1)抛物线的解析式为:y=-x2+2x+3
(2)该抛物线的对称轴为x= 1。设Q点坐标为(1,m)
当AB=AQ时 Q点坐标(1,?6),或(1,-?6);
当BA= BQ时 解得:m=0,m =6, Q点坐标为(1,0)或(1,6) 此点在直线AB上,不符合题意应舍去; 当QA=QB时 解得:m=1, Q点坐标为(1,1).
抛物线的对称轴上是存在着点Q(1,?6)、(1,-?6)、(1,0)、(1,1)
跟踪训练:
1.抛物线y=ax2﹣4ax+3a交x轴于点B、C两点,交y轴于点A,点D为抛物线的顶点,连接AB、AC,已知△ABC的面积为3.
(1)求抛物线的解析式;
(2)点P为抛物线对称轴右侧一点,点P的横坐标为m,过点P作PQ∥AC交y轴于点Q,AQ的长度为d,求d与m的函数关系式;
(3)在(2)的条件下,当d=4时,作DN⊥y轴于点N,点G为抛物线上一点,AG交线段PD于点M,连接MN,若△AMN是以MN为底的等腰三角形,求点G的坐标.
2.如图,抛物线y=﹣x2﹣x+c与x轴交于A,B两点,且点B的坐标为(3,0),与y轴交于点C,连接AC,BC,点P是抛物线上在第二象限内的一个动点,点P的横坐标为a,过点P作x轴的垂线,交AC于点Q.
(1)求A,C两点的坐标.
(2)请用含a的代数式表示线段PQ的长,并求出a为何值时PQ取得最大值.
(3)试探究在点P运动的过程中,是否存在这样的点Q,使得以B,C,Q为顶点的三角形是等腰三角形?若存在,请写出此时点Q的坐标;若不存在,请说明理由.
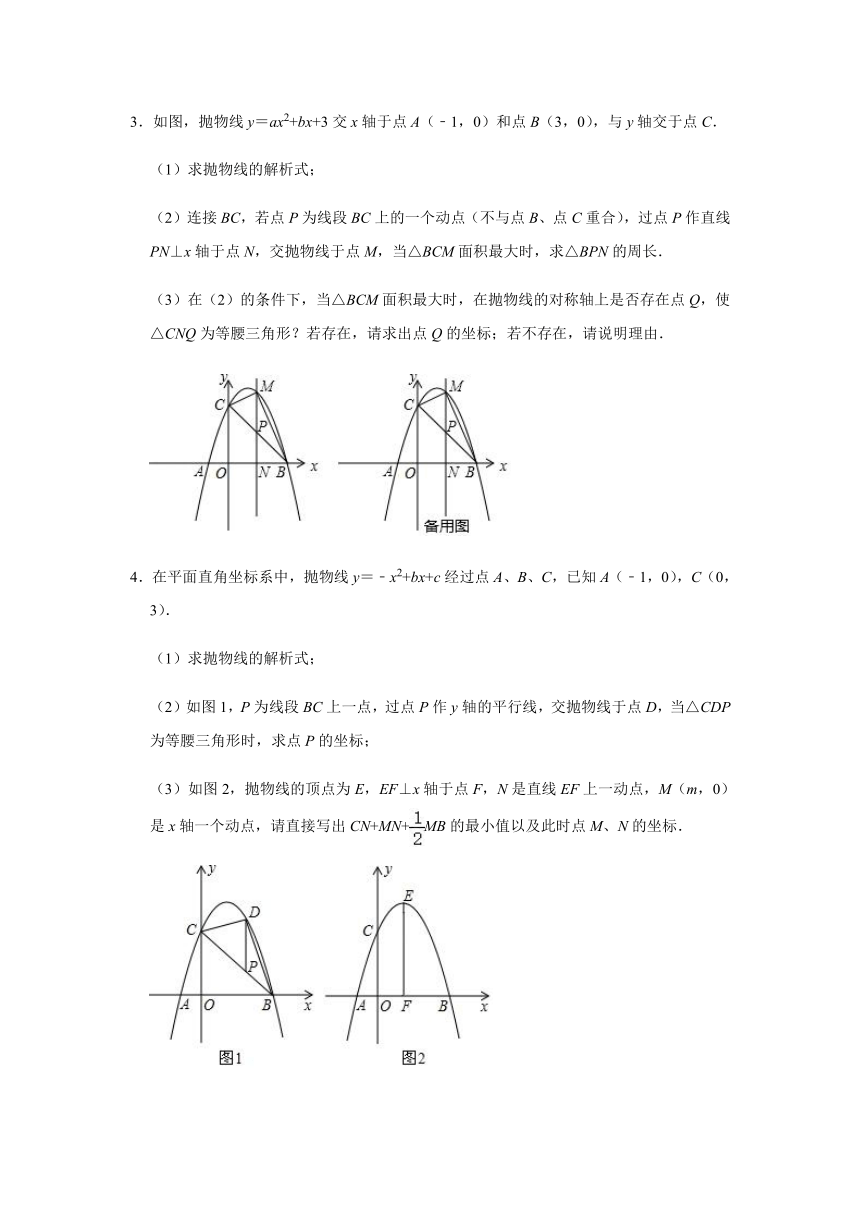
3.如图,抛物线y=ax2+bx+3交x轴于点A(﹣1,0)和点B(3,0),与y轴交于点C.
(1)求抛物线的解析式;
(2)连接BC,若点P为线段BC上的一个动点(不与点B、点C重合),过点P作直线PN⊥x轴于点N,交抛物线于点M,当△BCM面积最大时,求△BPN的周长.
(3)在(2)的条件下,当△BCM面积最大时,在抛物线的对称轴上是否存在点Q,使△CNQ为等腰三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.
4.在平面直角坐标系中,抛物线y=﹣x2+bx+c经过点A、B、C,已知A(﹣1,0),C(0,3).
(1)求抛物线的解析式;
(2)如图1,P为线段BC上一点,过点P作y轴的平行线,交抛物线于点D,当△CDP为等腰三角形时,求点P的坐标;
(3)如图2,抛物线的顶点为E,EF⊥x轴于点F,N是直线EF上一动点,M(m,0)是x轴一个动点,请直接写出CN+MN+MB的最小值以及此时点M、N的坐标.
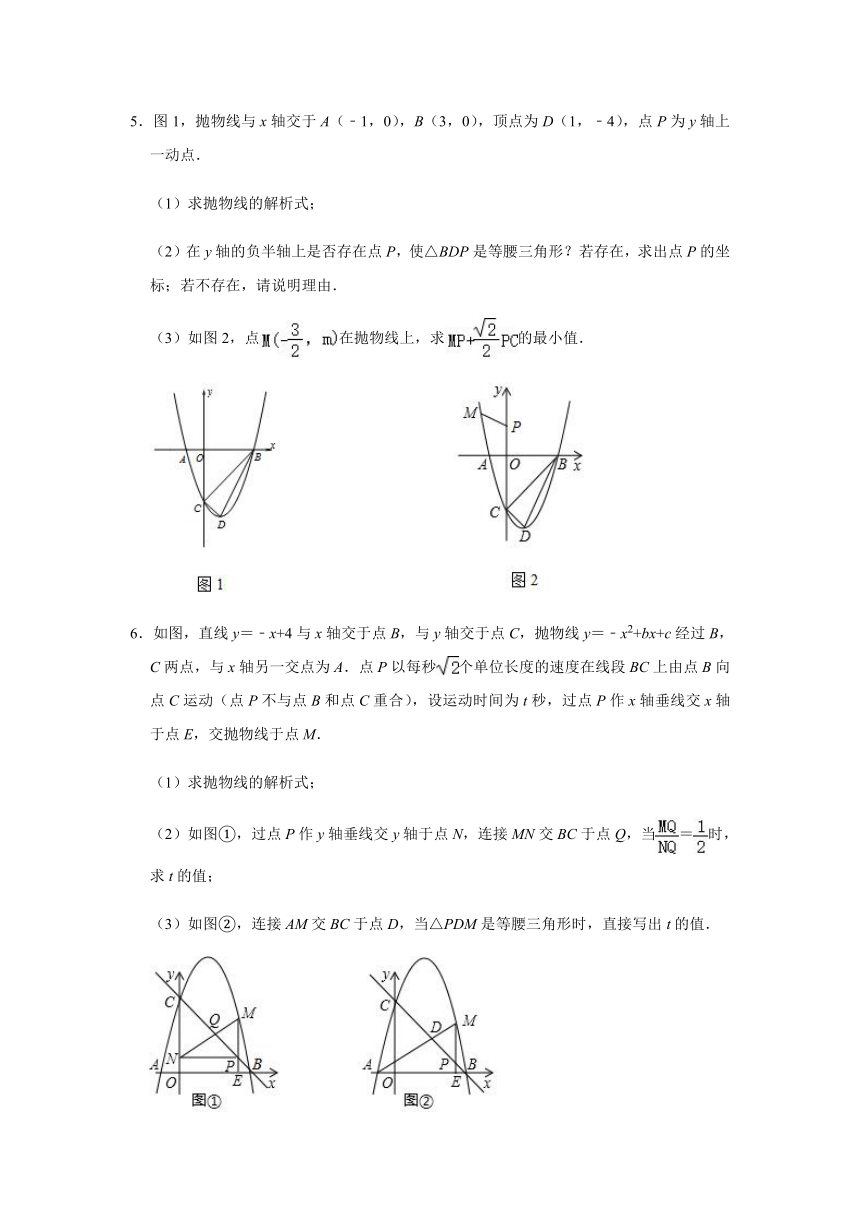
5.图1,抛物线与x轴交于A(﹣1,0),B(3,0),顶点为D(1,﹣4),点P为y轴上一动点.
(1)求抛物线的解析式;
(2)在y轴的负半轴上是否存在点P,使△BDP是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.
(3)如图2,点在抛物线上,求的最小值.
6.如图,直线y=﹣x+4与x轴交于点B,与y轴交于点C,抛物线y=﹣x2+bx+c经过B,C两点,与x轴另一交点为A.点P以每秒个单位长度的速度在线段BC上由点B向点C运动(点P不与点B和点C重合),设运动时间为t秒,过点P作x轴垂线交x轴于点E,交抛物线于点M.
(1)求抛物线的解析式;
(2)如图①,过点P作y轴垂线交y轴于点N,连接MN交BC于点Q,当=时,求t的值;
(3)如图②,连接AM交BC于点D,当△PDM是等腰三角形时,直接写出t的值.
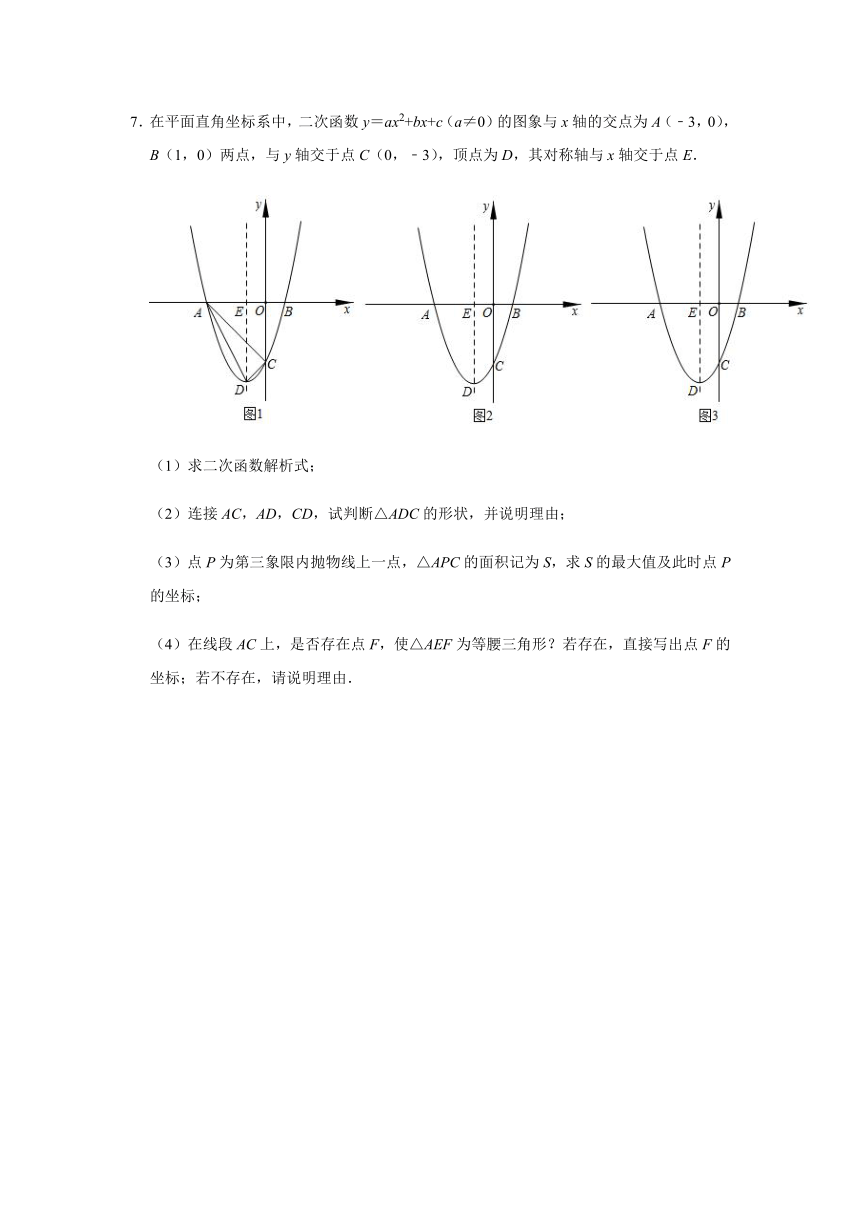
7.在平面直角坐标系中,二次函数y=ax2+bx+c(a≠0)的图象与x轴的交点为A(﹣3,0),B(1,0)两点,与y轴交于点C(0,﹣3),顶点为D,其对称轴与x轴交于点E.
(1)求二次函数解析式;
(2)连接AC,AD,CD,试判断△ADC的形状,并说明理由;
(3)点P为第三象限内抛物线上一点,△APC的面积记为S,求S的最大值及此时点P的坐标;
(4)在线段AC上,是否存在点F,使△AEF为等腰三角形?若存在,直接写出点F的坐标;若不存在,请说明理由.
8.抛物线y=ax2+bx+分别交x轴于点A(1,0),B(﹣3,0),交y轴于点C.抛物线的对称轴l与x轴相交于点D,直线AC与抛物线的对称轴l相交于点P.
(1)请直接写出抛物线的解析式和点D的坐标;
(2)如图1,点M为线段OC上的动点,点N为线段AC上的动点,且MN⊥AC,在点M,点N移动的过程中,DM+MC是否有最小值?如果有,请求出最小值;
(3)以点C为旋转中心,将直线AC绕点C逆时针旋转,旋转角为α(0°<α≤90°),直线AC旋转时,与抛物线的对称轴l相交于点E,与抛物线的另一个交点为点Q.
①如图2,当直线AC旋转到与直线BC重合时,判断线段PE、ED的数量关系?并说明理由;
②当△CPQ为等腰三角形时,请直接写出点Q的坐标.
9.如图,抛物线y=x2+bx+c与y轴交于点C,与x轴相交于A,B两点,点A的坐标为(2,0),点C的坐标为(0,﹣4).
(1)求该抛物线的解析式;
(2)点Q是线段BA上的一动点,点E为线段AC上一动点,若始终保持∠AQE=∠ABC,连接CQ,求△CQE的面积S关于点Q的横坐标m的函数关系式;
(3)若点D为OB的中点,点M是线段BC上一点,当△OMD为等腰三角形时,直接写出点M的坐标.
10.已知:如图,抛物线y=ax2+bx+3与坐标轴分别交于点A,B(﹣3,0),C(1,0),点P是线段AB上方抛物线上的一个动点.
(1)求抛物线解析式;
(2)当点P运动到什么位置时,△PAB的面积最大?
(3)过点P作x轴的垂线,交线段AB于点D,再过点P作PE∥x轴交抛物线于点E,连接DE,请问是否存在点P使△PDE为等腰直角三角形?若存在,求点P的坐标;若不存在,说明理由.
11.抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B(5,0)两点,顶点为C,对称轴交x轴于点D,点P为抛物线对称轴CD上的一动点(点P不与C,D重合).过点C作直线PB的垂线交PB于点E,交x轴于点F.
(1)求抛物线的解析式;
(2)当△PCF的面积为5时,求点P的坐标;
(3)当△PCF为等腰三角形时,请直接写出点P的坐标.
12.如图,在平面直角坐标系中,抛物线y=ax2+bx+c与x轴交于A(﹣1,0)、B(3,0)两点,且抛物线经过点D(2,3).
(1)求这条抛物线的表达式;
(2)将该抛物线向下平移,使得新抛物线的顶点G在x轴上.原抛物线上一点M平移后的对应点为点N,如果△AMN是以MN为底边的等腰三角形,求点N的坐标;
(3)若点P为抛物线上第一象限内的动点,过点B作BE⊥OP,垂足为E,点Q为y轴上的一个动点,连接QE、QD,试求QE+QD的最小值.
13.如图,菱形ABCD在平面直角坐标系中,边AB在x轴的负半轴上,点C在y轴的正半轴上,AB=10,tan∠DAB=,抛物线经过点B、C、D.
(1)求抛物线的解析式;
(2)直线EF与BC平行,与抛物线只有一个交点,求直线EF解析式;
(3)抛物线对称轴上是否存在点P,使△PBC是以BC为腰的等腰三角形?若存在直接写出P点坐标,若不存在说明理由.
参考答案
1.分析:(1)y=ax2﹣4ax+3a交x轴于点B、C两点,交y轴于点A,则点B、C的坐标分别为:(1,0)、(3,0),点A(0,3a),△ABC的面积=AB×OA=3a=3,即可求解;
(2)PQ平行线于AC直线,其表达式设为:y=﹣x+b,设点P(m,m2﹣4m+3)(m>2),将点P的坐标代入上式,即可求解;
(3)d=4时,点P(4,3),设点G(n,n2﹣4n+3),直线PD的函数表达式为:y=2x﹣5…①,直线AG的函数表达式为:y=(n﹣4)x+3…②,联立①②并解得:x=,故点M(,﹣5),AN=AM,即4+9=()2+(﹣8)2,即可求解.
解:(1)y=ax2﹣4ax+3a交x轴于点B、C两点,交y轴于点A,
则点B、C的坐标分别为:(1,0)、(3,0),点A(0,3a),
△ABC的面积=AB×OA=3a=3,解得:a=1,
故抛物线的表达式为:y=x2﹣4x+3;
(2)点A(0,3),点C(3,0),D(2,﹣1),
则PQ平行线于AC直线,其表达式设为:y=﹣x+b,
设点P(m,m2﹣4m+3)(m>2),
将点P的坐标代入上式并解得:b=m2﹣3m﹣3,
则d=AQ=|m2﹣3m|(m>2);
(3)当d=4时,|m2﹣3m|=4,
解得:m=4或﹣1(舍去﹣1),故点P(4,3),
设点G(n,n2﹣4n+3),点D(2,﹣1),则点N(0,﹣1)
同理可得:直线PD的函数表达式为:y=2x﹣5…①,
直线AG的函数表达式为:y=(n﹣4)x+3…②,
联立①②并解得:x=,故点M(,﹣5),
点A(0,3)、点N(0,﹣1),
AN=AM,即16=()2+(﹣8)2,
解得:n=或4,
故点G(,﹣)或(4,3).
点评:本题考查的是二次函数综合运用,涉及到一次函数、等腰三角形的性质、图形的面积计算等,其中(2),要注意分类求解,避免遗漏.
2.分析:(1)将点B的坐标(3,0)代入抛物线解析式可得出c=4,解方程,得x1=3,x2=﹣4,则A(﹣4,0);
(2)求出直线AC的解析式y=﹣x+4,设P(a,),则点Q(a,a+4),则PQ可用a表示,由二次函数的性质可求出PQ的最大值;
(3)分BC=BQ、BC=CQ、CQ=BQ三种情况,分别列得出方程求解即可.
解:(1)把点B的坐标(3,0)代入抛物线解析式得,
,
解得:c=4,
令y=0,则,
解得x1=3,x2=﹣4,
∴A(﹣4,0),C(0,4);
(2)∵A(﹣4,0),C(0,4),
设直线AC的解析式为y=kx+b,
∴,
∴,
∴直线AC的解析式y=x+4,
点P的横坐标为a,P(a,),则点Q(a,a+4),
∴PQ==,
∵,
∴a=﹣2时,PQ有最大值;
(3)存在,理由:
点A、B、C的坐标分别为(﹣4,0)、(3,0)、(0,4),
则BC=5,AB=7,AC=4,∠OAC=∠OCA=45°,
将点B、C的坐标代入一次函数表达式:y=mx+n并解得:,
∴直线BC的解析式为y=﹣x+4,
设BC的中点为H,由中点坐标公式可得H(),
∴过BC的中点H且与直线BC垂直直线的表达式为:y=,
①当BC=BQ时,如图1,
∴BC=BQ=5,
设:QM=AM=n,则BM=7﹣n,
由勾股定理得:(7﹣n)2+n2=25,
解得:n=3或4(舍去4),
故点Q1(﹣1,3);
②当BC=CQ时,如图1,
∴CQ=5,
则AQ=AC﹣CQ=4,
∴,
∴,
③当CQ=BQ时,
联立直线AC解析式y=x+4和y=,
解得x=﹣(不合题意,舍去),
综合以上可得点Q的坐标为:Q(﹣1,3)或().
点评:主要考查了二次函数的解析式的求法,等腰三角形的判定与性质,二次函数的性质等知识点,要会利用数形结合的思想把代数和几何图形结合起来,利用点的坐标的意义表示线段的长度,从而求出线段之间的关系.
3.分析:(1)由A、B两点的坐标,利用待定系数法即可求得抛物线解析式;
(2)先求出直线BC的解析式,设P(x,﹣x+3),则M(x,﹣x2+2x+3),求出△BCM面积的表达式,这是一个二次函数,求出其取最大值的条件;然后利用勾股定理可求出△BPN的周长;
(3)由(2)可知N(),设Q(1,a),由两点间的距离公式可分别表示出CQ2,QN2,CN2,若△CNQ为等腰三角形,可分CQ=QN、CQ=CN、QN=CN三种情况考虑,由此可得到关于a的方程,解方程求出符合题意的坐标即可.
解:(1)由题意可得:
,
解得,
∴抛物线解析式为y=﹣x2+2x+3;
(2)设直线BC的解析式为:y=kx+b,则有:
,
解得:,
∴直线BC的解析式为:y=﹣x+3.
设P(x,﹣x+3),则M(x,﹣x2+2x+3),
∴PM=(﹣x2+2x+3)﹣(﹣x+3)=﹣x2+3x.
∴S△BCM=S△PMC+S△PMB=(xB﹣xC)=,
∴S△BCM==,
∴当x=时,△BCM的面积最大.
此时P(),
∴PN=ON=,
∴BN=OB﹣ON=3﹣=,
在Rt△BPN中,由勾股定理得:PB=,
C△BCN=BN+PN+PB=3+,
∴当△BCM的面积最大时,△BPN的周长为3+;
(3)由(2)知P点坐标为(),
∴,
∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴抛物线的对称轴为x=1,
设Q(1,a),
∵C(0,3),N(),
∴CQ2=12+(3﹣a)2,,,
若△CNQ为等腰三角形,可分三种情况:
当CQ=QN时,1+,
解得:a=,
∴点Q的坐标为(1,),
当CQ=CN时,1+,
解得:a=3,
∴点Q的坐标为(1,3﹣),(1,3+),
当QN=CN时,,
解得:a=,
∴点Q的坐标为(1,),(1﹣),
综合以上可得点Q的坐标为(1,)或(1,3﹣)或(1,3+)或(1,)或(1,﹣).
点评:本题为二次函数的综合应用,涉及待定系数法、三角形的面积、二次函数的性质、等腰三角形的性质及分类讨论思想等知识.把代数和几何图形结合起来,利用点的坐标的意义表示线段的长度是解题的关键.
4.分析:(1)利用待定系数法即可求得此抛物线的解析式;
(2)由待定系数法即可求得直线BC的解析式,再设P(t,3﹣t),即可得D(t,﹣t2+2t+3),即可求得PD的长,然后分三种情况讨论,求点P的坐标;
(3)如图2,构造BG与x轴成30°角,将MB转化为线段M到BG的距离,从而可知C、M、N、B′在同一条直线上时,CN+MN+MB取最小值,根据CG的长和∠CGB=60°即可求出最小值.根据直线BG求出直线CB′解析式,即求出MN坐标.
解:(1)∵抛物线y=﹣x2+bx+c经过点A、B、C,把A(﹣1,0),C(0,3)代入解析式得,
∴,
解得b=2,c=3.
故该抛物线解析式为:y=﹣x2+2x+3.
(2)令﹣x2+2x+3=0,
解得x1=﹣1,x2=3,
即B(3,0),
设直线BC的解析式为y=kx+b′,
则,
解得:,
故直线BC的解析式为y=﹣x+3;
∴设P(t,3﹣t),
∴D(t,﹣t2+2t+3),
∴PD=(﹣t2+2t+3)﹣(3﹣t)=﹣t2+3t,
∵OB=OC=3,
∴△BOC是等腰直角三角形,
∴∠OCB=45°,
当CD=PC时,则∠CPD=∠CDP,
∵PD∥y轴,
∴∠CPD=∠OCB=45°,
∴∠CDP=45°,
∴∠PCD=90°,
∴直线CD的解析式为y=x+3,
解 得 或,
∴D(1,4),
此时P(1,2);
当CD=PD时,则∠DCP=∠CPD=45°,
∴∠CDP=90°,
∴CD∥x轴,
∴D点的纵坐标为3,
代入y=﹣x2+2x+3得,3=﹣x2+2x+3,
解得x=0或x=2,
此时P(2,1);
当PC=PD时,∵PC=t,
∴t=﹣t2+3t,
解得t=0或t=3﹣,
此时P(3﹣,);
综上,当△CDP为等腰三角形时,点P的坐标为(1,2)或(2,1)或(3﹣,).
(3)CN+MN+MB的最小值为,N坐标为(1,3﹣),M坐标为(,0).
理由如下:
如图,取G点坐标为(0,﹣),连接BG,
∵B(3,0),
∴直线BG解析式为:y=,
∴tan∠GBO=,∴∠GBO=30°,
过M点作MB′⊥BG,∴,
∴CN+MN+MB=CN+MN+B′M,
∴CN+MN+MB取最小值时,C、M、N、B′在同一条直线上,
即CB′⊥BG,
设直线CB′解析式为,∵C(0,3)
故直线CB′解析式为为,
∵抛物线的顶点为E坐标为(1,4),EF⊥x轴,N在EF、CB′上,
∴N坐标为(1,3﹣),
M(m,0)是x轴一个动点,也是CB′与x轴交点,
∴M(,0).
∵CG=3+,∠CGB=60°,
∴CB′=CGsin∠CGB=(3+)×=,
综上所述:CN+MN+MB的最小值为,N坐标为(1,3﹣),M坐标为(,0).
点评:此题考查了待定系数法求函数的解析式、平行线的性质、二次函数的最值问题、判别式的应用以及等腰直角三角形的性质等知识.此题综合性很强,难度较大,注意掌握数形结合思想、分类讨论思想与方程思想的应用.
5.分析:(1)由已知抛物线顶点D可设抛物线顶点式,再把点A代入即求得二次项系数a的值.
(2)由点B、D坐标可求BD的长.设点P坐标为(0,t),用t表示BP2,DP2.对BP=BD、DP=BD、BP=DP三种情况进行分类讨论计算,解方程求得t的值并讨论是否合理.
(3)由点B、C坐标可得∠BCO=45°,所以过点P作BC垂线段PQ即构造出等腰直角△PQC,可得PQ=PC,故有MP+PC=MP+PQ.过点M作BC的垂线段MH,根据垂线段最短性质,可知当点M、P、Q在同一直线上时,MP+PC=MP+PQ=MH最小,即需求MH的长.连接MB、MC构造△BCM,利用y轴分成△BCD与△CDM求面积和即得到△BCM面积,再由S△BCM=BC?MH即求得MH的长.
解:(1)∵抛物线顶点为D(1,﹣4)
∴设顶点式为y=a(x﹣1)2﹣4
∵A(﹣1,0)在抛物线上
∴4a﹣4=0,解得:a=1
∴抛物线的解析式为y=(x﹣1)2﹣4=x2﹣2x﹣3
(2)在y轴的负半轴上存在点P,使△BDP是等腰三角形.
∵B(3,0),D(1,﹣4)
∴BD2=(3﹣1)2+(0+4)2=20
设y轴负半轴的点P坐标为(0,t)(t<0)
∴BP2=32+t2,DP2=12+(t+4)2
①若BP=BD,则9+t2=20
解得:t1=(舍去),t2=﹣
②若DP=BD,则1+(t+4)2=20
解得:t1=(舍去),t2=﹣﹣4
③若BP=DP,则9+t2=1+(t+4)2
解得:t=﹣1
综上所述,点P坐标为(0,﹣)或(0,﹣﹣4)或(0,﹣1)
(3)连接MC、MB,MB交y轴于点D,过点P作PQ⊥BC于点Q,过点M作MH⊥BC于点H
∵x=0时,y=x2﹣2x﹣3=﹣3
∴C(0.﹣3)
∵B(3,0),∠BOC=90°
∴∠OBC=∠OCB=45°,BC=3
∵∠PQC=90°
∴Rt△PQC中,sin∠BCO==
∴PQ=PC
∴MP+PC=MP+PQ
∵MH⊥BC于点H
∴当点M、P、Q在同一直线上时,MP+PC=MP+PQ=MH最小
∵M(﹣,m)在抛物线上
∴m=(﹣)2﹣2×(﹣)﹣3=
∴M(﹣,)
设直线MB解析式为y=kx+b
∴ 解得:
∴直线MB:y=﹣x+
∴MB与y轴交点D(0,)
∴CD=﹣(﹣3)=
∴S△BCM=S△BCD+S△CDM=CD?BO+CD?|xM|=CD?(xB﹣xM)=××(3+)=
∵S△BCM=BC?MH
∴MH=
∴MP+PC的最小值为
点评:本题考查了二次函数的图象与性质,等腰三角形和等腰直角三角形的性质,解二元一次方程组和一元二次方程,垂线段最短定理.求线段和最小值时,一般利用特殊三角函数应用把含有系数的线段长进行转换,再利用三点成一直线或垂线段最短性质得到最短路径的位置,进而计算.
6.分析:(1)求直线y=﹣x+4与x轴交点B,与y轴交点C,用待定系数法即求得抛物线解析式.
(2)根据点B、C坐标求得∠OBC=45°,又PE⊥x轴于点E,得到△PEB是等腰直角三角形,由PB=t求得BE=PE=t,即可用t表示各线段,得到点M的横坐标,进而用m表示点M纵坐标,求得MP的长.根据MP∥CN可证△MPQ∽△NCQ,故有,把用t表示的MP、NC代入即得到关于t的方程,求解即得到t的值.
(3)因为不确定等腰△PDM的底和腰,故需分3种情况讨论:①若MD=MP,则∠MDP=∠MPD=45°,故有∠DMP=90°,不合题意;②若DM=DP,则∠DMP=∠MPD=45°,进而得AE=ME,把含t的式子代入并解方程即可;③若MP=DP,则∠PMD=∠PDM,由对顶角相等和两直线平行内错角相等可得∠CFD=∠PMD=∠PDM=∠CDF进而得CF=CD.用t表示M的坐标,求直线AM解析式,求得AM与y轴交点F的坐标,即能用t表示CF的长.把直线AM与直线BC解析式联立方程组,解得x的值即为点D横坐标.过D作y轴垂线段DG,得等腰直角△CDG,用DG即点D横坐标,进而可用t表示CD的长.把含t的式子代入CF=CD,解方程即得到t的值.
解:(1)直线y=﹣x+4中,当x=0时,y=4
∴C(0,4)
当y=﹣x+4=0时,解得:x=4
∴B(4,0)
∵抛物线y=﹣x2+bx+c经过B,C两点
∴ 解得:
∴抛物线解析式为y=﹣x2+3x+4
(2)∵B(4,0),C(0,4),∠BOC=90°
∴OB=OC
∴∠OBC=∠OCB=45°
∵ME⊥x轴于点E,PB=t
∴∠BEP=90°
∴Rt△BEP中,sin∠PBE=
∴BE=PE=PB=t
∴xM=xP=OE=OB﹣BE=4﹣t,yP=PE=t
∵点M在抛物线上
∴yM=﹣(4﹣t)2+3(4﹣t)+4=﹣t2+5t
∴MP=yM﹣yP=﹣t2+4t
∵PN⊥y轴于点N
∴∠PNO=∠NOE=∠PEO=90°
∴四边形ONPE是矩形
∴ON=PE=t
∴NC=OC﹣ON=4﹣t
∵MP∥CN
∴△MPQ∽△NCQ
∴
∴
解得:t1=,t2=4(点P不与点C重合,故舍去)
∴t的值为
(3)∵∠PEB=90°,BE=PE
∴∠BPE=∠PBE=45°
∴∠MPD=∠BPE=45°
①若MD=MP,则∠MDP=∠MPD=45°
∴∠DMP=90°,即DM∥x轴,与题意矛盾
②若DM=DP,则∠DMP=∠MPD=45°
∵∠AEM=90°
∴AE=ME
∵y=﹣x2+3x+4=0时,解得:x1=﹣1,x2=4
∴A(﹣1,0)
∵由(2)得,xM=4﹣t,ME=yM=﹣t2+5t
∴AE=4﹣t﹣(﹣1)=5﹣t
∴5﹣t=﹣t2+5t
解得:t1=1,t2=5(0<t<4,舍去)
③若MP=DP,则∠PMD=∠PDM
如图,记AM与y轴交点为F,过点D作DG⊥y轴于点G
∴∠CFD=∠PMD=∠PDM=∠CDF
∴CF=CD
∵A(﹣1,0),M(4﹣t,﹣t2+5t),设直线AM解析式为y=ax+m
∴ 解得:
∴直线AM:y=tx+t
∴F(0,t)
∴CF=OC﹣OF=4﹣t
∵tx+t=﹣x+4,解得:x=
∴DG=xD=
∵∠CGD=90°,∠DCG=45°
∴CD=DG=
∴4﹣t=
解得:t=﹣1
综上所述,当△PDM是等腰三角形时,t=1或t=﹣1.
点评:本题考查了二次函数的图象与性质,解二元一次方程组和一元二次方程,等腰直角三角形的性质,相似三角形的判定和性质,涉及等腰三角形的分类讨论,要充分利用等腰的性质作为列方程的依据.
7.分析:(1)二次函数表达式为:y=a(x+3)(x﹣1)=a(x2+2x﹣3),则﹣3a=﹣3,解得:a=1,即可求解;
(2)由AD2=AC2+CD2,故△ADC为直角三角形;
(3)S=PH×OA=(﹣x﹣3﹣x2﹣2x+3)=﹣(x+)2+,即可求解;
(4)分AE=EF、AE=AF、AF=EF三种情况分别求解即可.
解:(1)二次函数表达式为:y=a(x+3)(x﹣1)=a(x2+2x﹣3),
则﹣3a=﹣3,解得:a=1,
函数的表达式为:y=x2+2x﹣3;
(2)由(1)知,点D(﹣1,﹣4),
AC=3,CD=,AD==,
∴AD2=AC2+CD2,
故△ADC为直角三角形;
(3)过点P作PH∥y轴交AC于点H,
将点A、C的坐标代入一次函数表达式并解得:
直线AC的表达式为:y=﹣x﹣3,
设点P(x,x2+2x﹣3),则点H(x,﹣x﹣3),
S=PH×OA=(﹣x﹣3﹣x2﹣2x+3)=﹣(x+)2+,
当x=﹣时,S最大值为,此时点P(﹣,﹣);
(4)∵OA=OC=3,∴∠OAC=∠OCA=45°,
①当AE=EF时,如下图,
△AEF为等腰直角三角形,AE=2=EF,
∴点F(﹣1,﹣2);
②当AE=AF时,
同理可得:点F(﹣3+,﹣);
③当AF=EF时,
同理可得:点F(﹣2,﹣1);
故点F的坐标为:(﹣1,﹣2)或(﹣3+,﹣)或(﹣2,﹣1).
点评:本题考查的是二次函数综合运用,涉及到等腰三角形的性质、勾股定理的运用、面积的计算等,其中(3),要注意分类求解,避免遗漏.
8.分析:(1)用待定系数法即求得抛物线解析式;用顶点坐标公式即求得对称轴直线,得到点D坐标.
(2)求点C坐标,利用三角函数求得∠OCA的度数.由MN垂直AC可把MC转化为MN,所以当点D、M、N在同一直线上时DM+MC=DM+MN,根据垂线段最短,可知过点D作DF⊥AC于点F,此时为DM+MN最短.求∠OAC的度数,利用三角函数即求得DF的长.
(3)①求直线BC解析式,把x=1代入即求得点E坐标,进而得DE的长.由∠PDA=90°,∠PAD=60°利用三角函数求得PD的长,进而得PE的长,求得PE=2ED.
②求直线AC解析式,求点P坐标,进而求PC的长.设抛物线上的点Q坐标为(t,﹣t2﹣t+)(t≠0),根据两点间距离公式即能用t表示PQ2,CQ2.由△CPQ为等腰三角形分三种情况讨论两腰相等,即列得关于t的方程,求解得t的值即得到点Q坐标.
解:(1)∵抛物线y=ax2+bx+经过点A(1,0),B(﹣3,0)
∴ 解得:
∴抛物线的解析式为:y=﹣x2﹣x+
∵对称轴为直线:x=﹣=﹣1
∴D(﹣1,0)
(2)在M,N移动的过程中,DM+MC有最小值.
如图1,过点D作DF⊥AC于点F
∵当x=0时,y=﹣x2﹣x+=
∴C(0,)
∵A(1,0)
∴在Rt△AOC中,tan∠OCA===
∴∠OCA=30°
∵MN⊥AC,即∠MNC=90°
∴MN=MC
∴DM+MC=DM+MN
∴当点D、M、N在同一直线上时,DM+MC=DM+MN=DF最小
∵∠OAC=90°﹣∠OCA=60°
∴在Rt△DAF中,sin∠OAC=
∴DF=AD=×(1+1)=
∴DM+MC的最小值为
(3)①PE=2ED,理由如下:
设直线BC的解析式为y=kx+b
∴ 解得:
∴直线BC的解析式为y=x+,
∵对称轴为直线:x=﹣1,点E在对称轴上
∴点E(﹣1,)
∴DE=
∵∠PDA=90°,∠PAD=60°
∴在Rt△PAD中,tan∠OAC=
∴PD=2
∴PE=PD﹣DE=2﹣=
∴PE=2ED
②设直线AC解析式为y=cx+
把点A(1,0)代入得:c+=0,解得:c=﹣
∴直线AC:y=﹣x+
∵直线AC与对称轴:直线x=﹣1的交点为P
∴P(﹣1,2)
∴PC==2
∵点Q在抛物线上
∴设点Q坐标为(t,﹣t2﹣t+)(t≠0)
∴PQ2=(t+1)2+(﹣t2﹣t+﹣2)2,CQ2=t2+(﹣t2﹣t+﹣)2
i)若PQ=PC,如图2
∴PE垂直平分CQ
∴QE=CE=1,yQ=yC=
∴Q(﹣2,)
ii)若PQ=CQ,则(t+1)2+(﹣t2﹣t+﹣2)2=t2+(﹣t2﹣t+﹣)2
解得:t1=﹣2,t2=﹣1
∴Q(﹣2,)或(﹣1,)
iii)若PC=CQ,则t2+(﹣t2﹣t+﹣)2=4
解得:t=﹣2
∴Q(﹣2,)
综上所述,当△CPQ为等腰三角形时点Q的坐标分别为(﹣2,),(﹣1,).
点评:本题考查了二次函数的图象与性质,求一次函数解析式,特殊角三角函数,垂线段最短,两点间距离公式,等腰三角形的性质.求线段与线段的几分之一的和的最小值,通常需要对几分之一线段长进行转换,再利用三点共线或垂线段最短等相关定理找到最小值时的位置.
9.分析:(1)将点A、C的坐标代入抛物线,利用待定系数法求二次函数解析式解答;
(2)先求出点B的坐标,再根据三角形的面积公式求出S△ABC,设Q(m,0),表示出QA,再判断出△AQE∽△ABC,然后根据相似三角形面积的比等于相似比的平方表示出S△AQE,再根据S△QCE=S△AQC﹣S△AQE整理得到关于m的函数关系;
(3)分①当DM=DO时,DO=DM=DB=2,∠OBC=∠BMD=45°,再求出∠BDM=90°,然后写出M点的坐标;
②当MD=MO时,过点M作MN⊥OD于点N,根据等腰三角形三线合一的性质可得点N为OD的中点,求出DN=ON=1,BN=BD+DN=3,再根据△BMN为等腰直角三角形求出MN=BN=3,然后写出M点的坐标;③当OD=OM时,根据△OBC为等腰直角三角形求出点O到BC的距离,然后与OD相比较判断出不存在.
解:(1)将点A(2,0),C(0,﹣4),分别代入y=x2+bx+c,
,
解得:,
∴抛物线的解析式为y=;
(2)令y=0,即x2+x﹣4=0,解得x1=﹣4,x2=2,
∴点B(﹣4,0),
AB=2﹣(﹣4)=2+4=6,
S△ABC=AB?OC==12,
设Q点坐标为(m,0),则QA=2﹣m.
∵∠AQE=∠ABC,
∴QE∥BC,
∴△AQE∽△ABC,
∴,
∴,
S△QCE=S△AQC﹣S△AQE=,
=﹣.
(3)△OMD为等腰三角形,可能有三种情形:
①当DM=DO时,DO=DM=DA=2,
所以,∠OBC=∠BMD=45°,
所以,∠BDM=90°,
所以,M点的坐标为(﹣2,﹣2);
②当MD=MO时,如图,过点M作MN⊥OD于点N,则点N为OD的中点,
∴DN=ON=1,BN=BD+DN=3,
又△BMN为等腰直角三角形,
∴MN=BN=3,
∴M点的坐标为(﹣1,﹣3);
③当OD=OM时,
∵△OBC为等腰直角三角形,
∴点O到BC的距离为×4=2,
即BC上的点与点O之间的最小距离为2,
∵2>2,
∴OD=OM的情况不存在,
综上所述,点M的坐标为(﹣2,﹣2)或(﹣1,﹣3).
点评:本题是二次函数综合题,主要考查了待定系数法求二次函数解析式,抛物线与x轴的交点问题,三角形的面积,相似三角形面积的比等于相似比的平方的性质,等腰三角形的性质,等腰直角三角形的性质,注意等腰三角形根据腰长的不同分情况讨论.
10.分析:(1)用待定系数法即可求抛物线解析式.
(2)设点P横坐标为t,过点P作PF∥y轴交AB于点F,求直线AB解析式,即能用t表示点F坐标,进而表示PF的长.把△PAB分成△PAF与△PBF求面积和,即得到△PAB面积与t的函数关系,配方即得到t为何值时,△PAB面积最大,进而求得此时点P坐标.
(3)设点P横坐标为t,即能用t表示PD的长.根据对称性可知点P、E关于抛物线对称轴对称,用中点坐标公式可得用t表示点E横坐标,进而用t表示PE的长(注意点P、E左右位置不确定,需分类讨论).由于△PDE要成为等腰直角三角形,∠DPE=90°,所以PD=PE,把含t的式子代入求值即得到点P坐标.
解:(1)∵抛物线y=ax2+bx+3过点B(﹣3,0),C(1,0)
∴ 解得:
∴抛物线解析式为y=﹣x2﹣2x+3
(2)过点P作PH⊥x轴于点H,交AB于点F
∵x=0时,y=﹣x2﹣2x+3=3
∴A(0,3)
∴直线AB解析式为y=x+3
∵点P在线段AB上方抛物线上
∴设P(t,﹣t2﹣2t+3)(﹣3<t<0)
∴F(t,t+3)
∴PF=﹣t2﹣2t+3﹣(t+3)=﹣t2﹣3t
∴S△PAB=S△PAF+S△PBF=PF?OH+PF?BH=PF?OB=(﹣t2﹣3t)=﹣(t+)2+
∴点P运动到坐标为(﹣,),△PAB面积最大
(3)存在点P使△PDE为等腰直角三角形
设P(t,﹣t2﹣2t+3)(﹣3<t<0),则D(t,t+3)
∴PD=﹣t2﹣2t+3﹣(t+3)=﹣t2﹣3t
∵抛物线y=﹣x2﹣2x+3=﹣(x+1)2+4
∴对称轴为直线x=﹣1
∵PE∥x轴交抛物线于点E
∴yE=yP,即点E、P关于对称轴对称
∴=﹣1
∴xE=﹣2﹣xP=﹣2﹣t
∴PE=|xE﹣xP|=|﹣2﹣2t|
∵△PDE为等腰直角三角形,∠DPE=90°
∴PD=PE
①当﹣3<t≤﹣1时,PE=﹣2﹣2t
∴﹣t2﹣3t=﹣2﹣2t
解得:t1=1(舍去),t2=﹣2
∴P(﹣2,3)
②当﹣1<t<0时,PE=2+2t
∴﹣t2﹣3t=2+2t
解得:t1=,t2=(舍去)
∴P(,)
综上所述,点P坐标为(﹣2,3)或(,)时使△PDE为等腰直角三角形.
点评:本题考查了二次函数的图象与性质,求二次函数最值,等腰直角三角形的性质,中点坐标公式,一元二次方程的解法.分类讨论进行计算时,要注意讨论求得的解是否符合分类条件,是否需要舍去.
11.分析:(1)函数的表达式为:y=﹣(x+1)(x﹣5),即可求解;
(2)确定PB、CE的表达式,联立求得点F(2﹣,0),S△PCF=×PC×DF=(2﹣m)(2﹣﹣2)=5,即可求解;
(3)分当CP=CF、CP=PF、CF=PF三种情况,分别求解即可.
解:(1)函数的表达式为:y=﹣(x+1)(x﹣5)=﹣x2+x+;
(2)抛物线的对称轴为x=2,则点C(2,2),
设点P(2,m),
将点P、B的坐标代入一次函数表达式:y=sx+t并解得:
函数PB的表达式为:y=﹣mx+,
∵CE⊥PB,故直线CE表达式中的k值为,
将点C的坐标代入一次函数表达式,
同理可得直线CE的表达式为:y=,
解得:x=2﹣,
故点F(2﹣,0),
S△PCF=×PC×DF=(2﹣m)(2﹣﹣2)=5,
解得:m=5或﹣3,
故点P(2,﹣3)或(2,5);
(3)由(2)确定的点F的坐标得:
CP2=(2﹣m)2,CF2=()2+4,PF2=()2+m2,
①当CP=CF时,即:(2﹣m)2=()2+4,解得:m=0或(0舍去),
②当CP=PF时,同理可得:m=,
③当CF=PF时,同理可得:m=±2(舍去2),
故点P(2,)或(2,﹣2)或(2,)或(2,)
点评:本题考查的是二次函数综合运用,涉及到一次函数、等腰三角形性质、图形的面积计算等,其中(3),要注意分类求解,避免遗漏.
12.分析:(1)由抛物线与x轴两交点设交点式,把点D代入即求得抛物线表达式.
(2)由原抛物线顶点式可知,向下平移4个单位后顶点落在x轴上,故MN=4且MN⊥x轴.由于△AMN为等腰三角形且MN为底边,故有x轴垂直平分MN,得到点N纵坐标为﹣2,代入新抛物线解析式解方程即求得点N横坐标.
(3)作点D关于y轴的对称点D',根据轴对称性质即有QD=QD',易得当点D'、Q、E在同一直线上时,QE+QD=QE+QD'=ED'最小.由于点E随点P运动也是一个动点,由∠OEB=90°且O、B是定点可得点E的运动轨迹为圆弧.故当点E运动到点D'与圆心所连线段上时,D'E最小.求出圆心F的坐标,即求出D'F和半径r,所以D'E=D'F﹣r,所求即为QE+QD的最小值.
解:(1)抛物线与x轴交于A(﹣1,0)、B(3,0)
∴设交点式为y=a(x+1)(x﹣3)
∵抛物线经过点D(2,3)
∴a(x+1)(x﹣3)=3
解得:a=﹣1
∴抛物线表达式为y=﹣(x+1)(x﹣3)=﹣x2+2x+3
(2)∵y=﹣x2+2x+3=﹣(x﹣1)2+4
∴向下平移后新抛物线为y=﹣(x﹣1)2,顶点G(1,0),即抛物线向下平移4个单位
∵原抛物线上一点M平移后的对应点为点N
∴MN=4,MN⊥x轴
∵△AMN是以MN为底边的等腰三角形,且点A在x轴上
∴x轴垂直平分MN
∴N的纵坐标为﹣2
∴﹣(x﹣1)2=﹣2
解得:x1=1+,x2=1﹣
∴点N坐标为(1+,﹣2)或(1﹣,﹣2)
(3)作点D关于y轴的对称点点D',连接D'Q,取OB中点F,连接D'F
∵D(2,3),点Q为y轴上的动点
∴D'(﹣2,3),QD=QD'
∴当点D'、Q、E在同一直线上时,QE+QD=QE+QD'=ED'最小
∵BE⊥OP于点E,P为抛物线上第一象限内的动点
∴∠OEB=90°
∴点E在以OB为直径的圆在第一象限内的弧上运动
∵圆心F(,0),r=
∴当点E在线段D'F上时,D'E=D'F﹣EF=﹣=最小
∴QE+QD的最小值为.
点评:本题考查了二次函数的图象与性质,平移的性质,等腰三角形的性质,解一元二次方程,轴对称求最短路径,圆周角定理,勾股定理.第(3)题求线段和最小值涉及的两条线段有2个动点,先由常规的轴对称求最短路径问题确定点D'、Q、E必须共线,再找出点E运动轨迹为圆弧而得到点E在D'与圆心连线上时D'E最小.
13.分析:(1)由菱形的性质可得AD∥BC,BC=AB=10,那么∠DAB=∠CBO,根据tan∠DAB=tan∠CBO==,求出B、C、D三点的坐标,利用待定系数法求出抛物线的解析式;
(2)利用待定系数法求出直线BC的解析式为y=x+8.根据EF∥BC,可设直线EF解析式为y=x+t,根据直线EF与抛物线只有一个交点,得出方程x2+x+8=x+t只有一个解,即△=0,求出t的值,得到直线EF的解析式;
(3)分别利用当CP=CB时,△PCB为等腰三角形;当BP=BC时,△PCB为等腰三角形,利用勾股定理列方程即可.
解:(1)∵四边形ABCD是菱形,
∴AD∥BC,BC=AB=10,
∴∠DAB=∠CBO,
∴tan∠DAB=tan∠CBO==,
∵BC=10,
∴CO=8,BO=6,
∴B(﹣6,0),C(0,8),D(﹣10,8).
设抛物线的解析式为y=ax2+bx+c,
∵抛物线经过点B、C、D,
∴,解得:,
∴抛物线的解析式为y=x2+x+8;
(2)设直线BC的解析式为y=mx+n,
代入B、C点,解得:,
∴y=x+8.
∵EF∥BC,
∴设直线EF解析式为y=x+t,
又∵直线EF与抛物线只有一个交点,
∴x2+x+8=x+t只有一个解,△=0,
解得:t=5,
∴直线EF解析式为x+5;
(3)∵y=x2+x+8=(x+5)2﹣,
∴对称轴为直线x=﹣5.
设抛物线的对称轴上存在点P(﹣5,y),使△PBC是以BC为腰的等腰三角形.
B(﹣6,0),C(0,8),BC=10.
分两种情况:
①如果CP=CB,那么52+(y﹣8)2=100,解得y=8±5;
②如果BP=BC时,那么(﹣5+6)2+(y﹣0)2=100,解得y=±3.
故抛物线对称轴上存在点P,使△PBC是以BC为腰的等腰三角形,此时P点坐标为(﹣5,8+5)或(﹣5,8﹣5)或(﹣5,3)或(﹣5,﹣3).
点评:本题是二次函数综合题,涉及到利用待定系数法求函数的解析式,菱形的性质,正切函数定义,一次函数图象与几何变换,直线与抛物线的交点,等腰三角形的判定,勾股定理等知识,综合性较强,难度适中.利用方程思想与分类讨论是解题的关键
与等腰三角形相关的压轴题(附答案)
方法提炼:
1、设出点坐标,利用等腰三角形的性质求边长;
2、当所给定长未说明是等腰三角形的底还是腰时,需分情况讨论:
①当定长为腰,找已知直线上满足条件的点时,以定长的某一端点为圆心,以定长为半径画弧,若所画弧与已知直线有交点且交点不是定长的另一端点时,交点即为所求的点;若所画弧与已知直线无交点或交点是定长的另一端点时,满足条件的点不存在;
②当定长为底边时,作出定长的垂直平分线,若作出的垂直平分线与已知直线有交点,则交点即为所求的点,若作出的垂直平分线与已知直线无交点,则满足条件的点不存在.用以上方法即可找出所有符合条件的点。
典例引领:
例:如图,直线y=3x+3交x轴于点A,交y轴于点B,过A、B两点的抛物线交x轴于另一点C(3,0)。
(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在点Q,使△ABQ是等腰三角形?若存在,求出符合条件的点Q的坐标;若不存在,请说明理由。
解:(1)抛物线的解析式为:y=-x2+2x+3
(2)该抛物线的对称轴为x= 1。设Q点坐标为(1,m)
当AB=AQ时 Q点坐标(1,?6),或(1,-?6);
当BA= BQ时 解得:m=0,m =6, Q点坐标为(1,0)或(1,6) 此点在直线AB上,不符合题意应舍去; 当QA=QB时 解得:m=1, Q点坐标为(1,1).
抛物线的对称轴上是存在着点Q(1,?6)、(1,-?6)、(1,0)、(1,1)
跟踪训练:
1.抛物线y=ax2﹣4ax+3a交x轴于点B、C两点,交y轴于点A,点D为抛物线的顶点,连接AB、AC,已知△ABC的面积为3.
(1)求抛物线的解析式;
(2)点P为抛物线对称轴右侧一点,点P的横坐标为m,过点P作PQ∥AC交y轴于点Q,AQ的长度为d,求d与m的函数关系式;
(3)在(2)的条件下,当d=4时,作DN⊥y轴于点N,点G为抛物线上一点,AG交线段PD于点M,连接MN,若△AMN是以MN为底的等腰三角形,求点G的坐标.
2.如图,抛物线y=﹣x2﹣x+c与x轴交于A,B两点,且点B的坐标为(3,0),与y轴交于点C,连接AC,BC,点P是抛物线上在第二象限内的一个动点,点P的横坐标为a,过点P作x轴的垂线,交AC于点Q.
(1)求A,C两点的坐标.
(2)请用含a的代数式表示线段PQ的长,并求出a为何值时PQ取得最大值.
(3)试探究在点P运动的过程中,是否存在这样的点Q,使得以B,C,Q为顶点的三角形是等腰三角形?若存在,请写出此时点Q的坐标;若不存在,请说明理由.
3.如图,抛物线y=ax2+bx+3交x轴于点A(﹣1,0)和点B(3,0),与y轴交于点C.
(1)求抛物线的解析式;
(2)连接BC,若点P为线段BC上的一个动点(不与点B、点C重合),过点P作直线PN⊥x轴于点N,交抛物线于点M,当△BCM面积最大时,求△BPN的周长.
(3)在(2)的条件下,当△BCM面积最大时,在抛物线的对称轴上是否存在点Q,使△CNQ为等腰三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.
4.在平面直角坐标系中,抛物线y=﹣x2+bx+c经过点A、B、C,已知A(﹣1,0),C(0,3).
(1)求抛物线的解析式;
(2)如图1,P为线段BC上一点,过点P作y轴的平行线,交抛物线于点D,当△CDP为等腰三角形时,求点P的坐标;
(3)如图2,抛物线的顶点为E,EF⊥x轴于点F,N是直线EF上一动点,M(m,0)是x轴一个动点,请直接写出CN+MN+MB的最小值以及此时点M、N的坐标.
5.图1,抛物线与x轴交于A(﹣1,0),B(3,0),顶点为D(1,﹣4),点P为y轴上一动点.
(1)求抛物线的解析式;
(2)在y轴的负半轴上是否存在点P,使△BDP是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.
(3)如图2,点在抛物线上,求的最小值.
6.如图,直线y=﹣x+4与x轴交于点B,与y轴交于点C,抛物线y=﹣x2+bx+c经过B,C两点,与x轴另一交点为A.点P以每秒个单位长度的速度在线段BC上由点B向点C运动(点P不与点B和点C重合),设运动时间为t秒,过点P作x轴垂线交x轴于点E,交抛物线于点M.
(1)求抛物线的解析式;
(2)如图①,过点P作y轴垂线交y轴于点N,连接MN交BC于点Q,当=时,求t的值;
(3)如图②,连接AM交BC于点D,当△PDM是等腰三角形时,直接写出t的值.
7.在平面直角坐标系中,二次函数y=ax2+bx+c(a≠0)的图象与x轴的交点为A(﹣3,0),B(1,0)两点,与y轴交于点C(0,﹣3),顶点为D,其对称轴与x轴交于点E.
(1)求二次函数解析式;
(2)连接AC,AD,CD,试判断△ADC的形状,并说明理由;
(3)点P为第三象限内抛物线上一点,△APC的面积记为S,求S的最大值及此时点P的坐标;
(4)在线段AC上,是否存在点F,使△AEF为等腰三角形?若存在,直接写出点F的坐标;若不存在,请说明理由.
8.抛物线y=ax2+bx+分别交x轴于点A(1,0),B(﹣3,0),交y轴于点C.抛物线的对称轴l与x轴相交于点D,直线AC与抛物线的对称轴l相交于点P.
(1)请直接写出抛物线的解析式和点D的坐标;
(2)如图1,点M为线段OC上的动点,点N为线段AC上的动点,且MN⊥AC,在点M,点N移动的过程中,DM+MC是否有最小值?如果有,请求出最小值;
(3)以点C为旋转中心,将直线AC绕点C逆时针旋转,旋转角为α(0°<α≤90°),直线AC旋转时,与抛物线的对称轴l相交于点E,与抛物线的另一个交点为点Q.
①如图2,当直线AC旋转到与直线BC重合时,判断线段PE、ED的数量关系?并说明理由;
②当△CPQ为等腰三角形时,请直接写出点Q的坐标.
9.如图,抛物线y=x2+bx+c与y轴交于点C,与x轴相交于A,B两点,点A的坐标为(2,0),点C的坐标为(0,﹣4).
(1)求该抛物线的解析式;
(2)点Q是线段BA上的一动点,点E为线段AC上一动点,若始终保持∠AQE=∠ABC,连接CQ,求△CQE的面积S关于点Q的横坐标m的函数关系式;
(3)若点D为OB的中点,点M是线段BC上一点,当△OMD为等腰三角形时,直接写出点M的坐标.
10.已知:如图,抛物线y=ax2+bx+3与坐标轴分别交于点A,B(﹣3,0),C(1,0),点P是线段AB上方抛物线上的一个动点.
(1)求抛物线解析式;
(2)当点P运动到什么位置时,△PAB的面积最大?
(3)过点P作x轴的垂线,交线段AB于点D,再过点P作PE∥x轴交抛物线于点E,连接DE,请问是否存在点P使△PDE为等腰直角三角形?若存在,求点P的坐标;若不存在,说明理由.
11.抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B(5,0)两点,顶点为C,对称轴交x轴于点D,点P为抛物线对称轴CD上的一动点(点P不与C,D重合).过点C作直线PB的垂线交PB于点E,交x轴于点F.
(1)求抛物线的解析式;
(2)当△PCF的面积为5时,求点P的坐标;
(3)当△PCF为等腰三角形时,请直接写出点P的坐标.
12.如图,在平面直角坐标系中,抛物线y=ax2+bx+c与x轴交于A(﹣1,0)、B(3,0)两点,且抛物线经过点D(2,3).
(1)求这条抛物线的表达式;
(2)将该抛物线向下平移,使得新抛物线的顶点G在x轴上.原抛物线上一点M平移后的对应点为点N,如果△AMN是以MN为底边的等腰三角形,求点N的坐标;
(3)若点P为抛物线上第一象限内的动点,过点B作BE⊥OP,垂足为E,点Q为y轴上的一个动点,连接QE、QD,试求QE+QD的最小值.
13.如图,菱形ABCD在平面直角坐标系中,边AB在x轴的负半轴上,点C在y轴的正半轴上,AB=10,tan∠DAB=,抛物线经过点B、C、D.
(1)求抛物线的解析式;
(2)直线EF与BC平行,与抛物线只有一个交点,求直线EF解析式;
(3)抛物线对称轴上是否存在点P,使△PBC是以BC为腰的等腰三角形?若存在直接写出P点坐标,若不存在说明理由.
参考答案
1.分析:(1)y=ax2﹣4ax+3a交x轴于点B、C两点,交y轴于点A,则点B、C的坐标分别为:(1,0)、(3,0),点A(0,3a),△ABC的面积=AB×OA=3a=3,即可求解;
(2)PQ平行线于AC直线,其表达式设为:y=﹣x+b,设点P(m,m2﹣4m+3)(m>2),将点P的坐标代入上式,即可求解;
(3)d=4时,点P(4,3),设点G(n,n2﹣4n+3),直线PD的函数表达式为:y=2x﹣5…①,直线AG的函数表达式为:y=(n﹣4)x+3…②,联立①②并解得:x=,故点M(,﹣5),AN=AM,即4+9=()2+(﹣8)2,即可求解.
解:(1)y=ax2﹣4ax+3a交x轴于点B、C两点,交y轴于点A,
则点B、C的坐标分别为:(1,0)、(3,0),点A(0,3a),
△ABC的面积=AB×OA=3a=3,解得:a=1,
故抛物线的表达式为:y=x2﹣4x+3;
(2)点A(0,3),点C(3,0),D(2,﹣1),
则PQ平行线于AC直线,其表达式设为:y=﹣x+b,
设点P(m,m2﹣4m+3)(m>2),
将点P的坐标代入上式并解得:b=m2﹣3m﹣3,
则d=AQ=|m2﹣3m|(m>2);
(3)当d=4时,|m2﹣3m|=4,
解得:m=4或﹣1(舍去﹣1),故点P(4,3),
设点G(n,n2﹣4n+3),点D(2,﹣1),则点N(0,﹣1)
同理可得:直线PD的函数表达式为:y=2x﹣5…①,
直线AG的函数表达式为:y=(n﹣4)x+3…②,
联立①②并解得:x=,故点M(,﹣5),
点A(0,3)、点N(0,﹣1),
AN=AM,即16=()2+(﹣8)2,
解得:n=或4,
故点G(,﹣)或(4,3).
点评:本题考查的是二次函数综合运用,涉及到一次函数、等腰三角形的性质、图形的面积计算等,其中(2),要注意分类求解,避免遗漏.
2.分析:(1)将点B的坐标(3,0)代入抛物线解析式可得出c=4,解方程,得x1=3,x2=﹣4,则A(﹣4,0);
(2)求出直线AC的解析式y=﹣x+4,设P(a,),则点Q(a,a+4),则PQ可用a表示,由二次函数的性质可求出PQ的最大值;
(3)分BC=BQ、BC=CQ、CQ=BQ三种情况,分别列得出方程求解即可.
解:(1)把点B的坐标(3,0)代入抛物线解析式得,
,
解得:c=4,
令y=0,则,
解得x1=3,x2=﹣4,
∴A(﹣4,0),C(0,4);
(2)∵A(﹣4,0),C(0,4),
设直线AC的解析式为y=kx+b,
∴,
∴,
∴直线AC的解析式y=x+4,
点P的横坐标为a,P(a,),则点Q(a,a+4),
∴PQ==,
∵,
∴a=﹣2时,PQ有最大值;
(3)存在,理由:
点A、B、C的坐标分别为(﹣4,0)、(3,0)、(0,4),
则BC=5,AB=7,AC=4,∠OAC=∠OCA=45°,
将点B、C的坐标代入一次函数表达式:y=mx+n并解得:,
∴直线BC的解析式为y=﹣x+4,
设BC的中点为H,由中点坐标公式可得H(),
∴过BC的中点H且与直线BC垂直直线的表达式为:y=,
①当BC=BQ时,如图1,
∴BC=BQ=5,
设:QM=AM=n,则BM=7﹣n,
由勾股定理得:(7﹣n)2+n2=25,
解得:n=3或4(舍去4),
故点Q1(﹣1,3);
②当BC=CQ时,如图1,
∴CQ=5,
则AQ=AC﹣CQ=4,
∴,
∴,
③当CQ=BQ时,
联立直线AC解析式y=x+4和y=,
解得x=﹣(不合题意,舍去),
综合以上可得点Q的坐标为:Q(﹣1,3)或().
点评:主要考查了二次函数的解析式的求法,等腰三角形的判定与性质,二次函数的性质等知识点,要会利用数形结合的思想把代数和几何图形结合起来,利用点的坐标的意义表示线段的长度,从而求出线段之间的关系.
3.分析:(1)由A、B两点的坐标,利用待定系数法即可求得抛物线解析式;
(2)先求出直线BC的解析式,设P(x,﹣x+3),则M(x,﹣x2+2x+3),求出△BCM面积的表达式,这是一个二次函数,求出其取最大值的条件;然后利用勾股定理可求出△BPN的周长;
(3)由(2)可知N(),设Q(1,a),由两点间的距离公式可分别表示出CQ2,QN2,CN2,若△CNQ为等腰三角形,可分CQ=QN、CQ=CN、QN=CN三种情况考虑,由此可得到关于a的方程,解方程求出符合题意的坐标即可.
解:(1)由题意可得:
,
解得,
∴抛物线解析式为y=﹣x2+2x+3;
(2)设直线BC的解析式为:y=kx+b,则有:
,
解得:,
∴直线BC的解析式为:y=﹣x+3.
设P(x,﹣x+3),则M(x,﹣x2+2x+3),
∴PM=(﹣x2+2x+3)﹣(﹣x+3)=﹣x2+3x.
∴S△BCM=S△PMC+S△PMB=(xB﹣xC)=,
∴S△BCM==,
∴当x=时,△BCM的面积最大.
此时P(),
∴PN=ON=,
∴BN=OB﹣ON=3﹣=,
在Rt△BPN中,由勾股定理得:PB=,
C△BCN=BN+PN+PB=3+,
∴当△BCM的面积最大时,△BPN的周长为3+;
(3)由(2)知P点坐标为(),
∴,
∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴抛物线的对称轴为x=1,
设Q(1,a),
∵C(0,3),N(),
∴CQ2=12+(3﹣a)2,,,
若△CNQ为等腰三角形,可分三种情况:
当CQ=QN时,1+,
解得:a=,
∴点Q的坐标为(1,),
当CQ=CN时,1+,
解得:a=3,
∴点Q的坐标为(1,3﹣),(1,3+),
当QN=CN时,,
解得:a=,
∴点Q的坐标为(1,),(1﹣),
综合以上可得点Q的坐标为(1,)或(1,3﹣)或(1,3+)或(1,)或(1,﹣).
点评:本题为二次函数的综合应用,涉及待定系数法、三角形的面积、二次函数的性质、等腰三角形的性质及分类讨论思想等知识.把代数和几何图形结合起来,利用点的坐标的意义表示线段的长度是解题的关键.
4.分析:(1)利用待定系数法即可求得此抛物线的解析式;
(2)由待定系数法即可求得直线BC的解析式,再设P(t,3﹣t),即可得D(t,﹣t2+2t+3),即可求得PD的长,然后分三种情况讨论,求点P的坐标;
(3)如图2,构造BG与x轴成30°角,将MB转化为线段M到BG的距离,从而可知C、M、N、B′在同一条直线上时,CN+MN+MB取最小值,根据CG的长和∠CGB=60°即可求出最小值.根据直线BG求出直线CB′解析式,即求出MN坐标.
解:(1)∵抛物线y=﹣x2+bx+c经过点A、B、C,把A(﹣1,0),C(0,3)代入解析式得,
∴,
解得b=2,c=3.
故该抛物线解析式为:y=﹣x2+2x+3.
(2)令﹣x2+2x+3=0,
解得x1=﹣1,x2=3,
即B(3,0),
设直线BC的解析式为y=kx+b′,
则,
解得:,
故直线BC的解析式为y=﹣x+3;
∴设P(t,3﹣t),
∴D(t,﹣t2+2t+3),
∴PD=(﹣t2+2t+3)﹣(3﹣t)=﹣t2+3t,
∵OB=OC=3,
∴△BOC是等腰直角三角形,
∴∠OCB=45°,
当CD=PC时,则∠CPD=∠CDP,
∵PD∥y轴,
∴∠CPD=∠OCB=45°,
∴∠CDP=45°,
∴∠PCD=90°,
∴直线CD的解析式为y=x+3,
解 得 或,
∴D(1,4),
此时P(1,2);
当CD=PD时,则∠DCP=∠CPD=45°,
∴∠CDP=90°,
∴CD∥x轴,
∴D点的纵坐标为3,
代入y=﹣x2+2x+3得,3=﹣x2+2x+3,
解得x=0或x=2,
此时P(2,1);
当PC=PD时,∵PC=t,
∴t=﹣t2+3t,
解得t=0或t=3﹣,
此时P(3﹣,);
综上,当△CDP为等腰三角形时,点P的坐标为(1,2)或(2,1)或(3﹣,).
(3)CN+MN+MB的最小值为,N坐标为(1,3﹣),M坐标为(,0).
理由如下:
如图,取G点坐标为(0,﹣),连接BG,
∵B(3,0),
∴直线BG解析式为:y=,
∴tan∠GBO=,∴∠GBO=30°,
过M点作MB′⊥BG,∴,
∴CN+MN+MB=CN+MN+B′M,
∴CN+MN+MB取最小值时,C、M、N、B′在同一条直线上,
即CB′⊥BG,
设直线CB′解析式为,∵C(0,3)
故直线CB′解析式为为,
∵抛物线的顶点为E坐标为(1,4),EF⊥x轴,N在EF、CB′上,
∴N坐标为(1,3﹣),
M(m,0)是x轴一个动点,也是CB′与x轴交点,
∴M(,0).
∵CG=3+,∠CGB=60°,
∴CB′=CGsin∠CGB=(3+)×=,
综上所述:CN+MN+MB的最小值为,N坐标为(1,3﹣),M坐标为(,0).
点评:此题考查了待定系数法求函数的解析式、平行线的性质、二次函数的最值问题、判别式的应用以及等腰直角三角形的性质等知识.此题综合性很强,难度较大,注意掌握数形结合思想、分类讨论思想与方程思想的应用.
5.分析:(1)由已知抛物线顶点D可设抛物线顶点式,再把点A代入即求得二次项系数a的值.
(2)由点B、D坐标可求BD的长.设点P坐标为(0,t),用t表示BP2,DP2.对BP=BD、DP=BD、BP=DP三种情况进行分类讨论计算,解方程求得t的值并讨论是否合理.
(3)由点B、C坐标可得∠BCO=45°,所以过点P作BC垂线段PQ即构造出等腰直角△PQC,可得PQ=PC,故有MP+PC=MP+PQ.过点M作BC的垂线段MH,根据垂线段最短性质,可知当点M、P、Q在同一直线上时,MP+PC=MP+PQ=MH最小,即需求MH的长.连接MB、MC构造△BCM,利用y轴分成△BCD与△CDM求面积和即得到△BCM面积,再由S△BCM=BC?MH即求得MH的长.
解:(1)∵抛物线顶点为D(1,﹣4)
∴设顶点式为y=a(x﹣1)2﹣4
∵A(﹣1,0)在抛物线上
∴4a﹣4=0,解得:a=1
∴抛物线的解析式为y=(x﹣1)2﹣4=x2﹣2x﹣3
(2)在y轴的负半轴上存在点P,使△BDP是等腰三角形.
∵B(3,0),D(1,﹣4)
∴BD2=(3﹣1)2+(0+4)2=20
设y轴负半轴的点P坐标为(0,t)(t<0)
∴BP2=32+t2,DP2=12+(t+4)2
①若BP=BD,则9+t2=20
解得:t1=(舍去),t2=﹣
②若DP=BD,则1+(t+4)2=20
解得:t1=(舍去),t2=﹣﹣4
③若BP=DP,则9+t2=1+(t+4)2
解得:t=﹣1
综上所述,点P坐标为(0,﹣)或(0,﹣﹣4)或(0,﹣1)
(3)连接MC、MB,MB交y轴于点D,过点P作PQ⊥BC于点Q,过点M作MH⊥BC于点H
∵x=0时,y=x2﹣2x﹣3=﹣3
∴C(0.﹣3)
∵B(3,0),∠BOC=90°
∴∠OBC=∠OCB=45°,BC=3
∵∠PQC=90°
∴Rt△PQC中,sin∠BCO==
∴PQ=PC
∴MP+PC=MP+PQ
∵MH⊥BC于点H
∴当点M、P、Q在同一直线上时,MP+PC=MP+PQ=MH最小
∵M(﹣,m)在抛物线上
∴m=(﹣)2﹣2×(﹣)﹣3=
∴M(﹣,)
设直线MB解析式为y=kx+b
∴ 解得:
∴直线MB:y=﹣x+
∴MB与y轴交点D(0,)
∴CD=﹣(﹣3)=
∴S△BCM=S△BCD+S△CDM=CD?BO+CD?|xM|=CD?(xB﹣xM)=××(3+)=
∵S△BCM=BC?MH
∴MH=
∴MP+PC的最小值为
点评:本题考查了二次函数的图象与性质,等腰三角形和等腰直角三角形的性质,解二元一次方程组和一元二次方程,垂线段最短定理.求线段和最小值时,一般利用特殊三角函数应用把含有系数的线段长进行转换,再利用三点成一直线或垂线段最短性质得到最短路径的位置,进而计算.
6.分析:(1)求直线y=﹣x+4与x轴交点B,与y轴交点C,用待定系数法即求得抛物线解析式.
(2)根据点B、C坐标求得∠OBC=45°,又PE⊥x轴于点E,得到△PEB是等腰直角三角形,由PB=t求得BE=PE=t,即可用t表示各线段,得到点M的横坐标,进而用m表示点M纵坐标,求得MP的长.根据MP∥CN可证△MPQ∽△NCQ,故有,把用t表示的MP、NC代入即得到关于t的方程,求解即得到t的值.
(3)因为不确定等腰△PDM的底和腰,故需分3种情况讨论:①若MD=MP,则∠MDP=∠MPD=45°,故有∠DMP=90°,不合题意;②若DM=DP,则∠DMP=∠MPD=45°,进而得AE=ME,把含t的式子代入并解方程即可;③若MP=DP,则∠PMD=∠PDM,由对顶角相等和两直线平行内错角相等可得∠CFD=∠PMD=∠PDM=∠CDF进而得CF=CD.用t表示M的坐标,求直线AM解析式,求得AM与y轴交点F的坐标,即能用t表示CF的长.把直线AM与直线BC解析式联立方程组,解得x的值即为点D横坐标.过D作y轴垂线段DG,得等腰直角△CDG,用DG即点D横坐标,进而可用t表示CD的长.把含t的式子代入CF=CD,解方程即得到t的值.
解:(1)直线y=﹣x+4中,当x=0时,y=4
∴C(0,4)
当y=﹣x+4=0时,解得:x=4
∴B(4,0)
∵抛物线y=﹣x2+bx+c经过B,C两点
∴ 解得:
∴抛物线解析式为y=﹣x2+3x+4
(2)∵B(4,0),C(0,4),∠BOC=90°
∴OB=OC
∴∠OBC=∠OCB=45°
∵ME⊥x轴于点E,PB=t
∴∠BEP=90°
∴Rt△BEP中,sin∠PBE=
∴BE=PE=PB=t
∴xM=xP=OE=OB﹣BE=4﹣t,yP=PE=t
∵点M在抛物线上
∴yM=﹣(4﹣t)2+3(4﹣t)+4=﹣t2+5t
∴MP=yM﹣yP=﹣t2+4t
∵PN⊥y轴于点N
∴∠PNO=∠NOE=∠PEO=90°
∴四边形ONPE是矩形
∴ON=PE=t
∴NC=OC﹣ON=4﹣t
∵MP∥CN
∴△MPQ∽△NCQ
∴
∴
解得:t1=,t2=4(点P不与点C重合,故舍去)
∴t的值为
(3)∵∠PEB=90°,BE=PE
∴∠BPE=∠PBE=45°
∴∠MPD=∠BPE=45°
①若MD=MP,则∠MDP=∠MPD=45°
∴∠DMP=90°,即DM∥x轴,与题意矛盾
②若DM=DP,则∠DMP=∠MPD=45°
∵∠AEM=90°
∴AE=ME
∵y=﹣x2+3x+4=0时,解得:x1=﹣1,x2=4
∴A(﹣1,0)
∵由(2)得,xM=4﹣t,ME=yM=﹣t2+5t
∴AE=4﹣t﹣(﹣1)=5﹣t
∴5﹣t=﹣t2+5t
解得:t1=1,t2=5(0<t<4,舍去)
③若MP=DP,则∠PMD=∠PDM
如图,记AM与y轴交点为F,过点D作DG⊥y轴于点G
∴∠CFD=∠PMD=∠PDM=∠CDF
∴CF=CD
∵A(﹣1,0),M(4﹣t,﹣t2+5t),设直线AM解析式为y=ax+m
∴ 解得:
∴直线AM:y=tx+t
∴F(0,t)
∴CF=OC﹣OF=4﹣t
∵tx+t=﹣x+4,解得:x=
∴DG=xD=
∵∠CGD=90°,∠DCG=45°
∴CD=DG=
∴4﹣t=
解得:t=﹣1
综上所述,当△PDM是等腰三角形时,t=1或t=﹣1.
点评:本题考查了二次函数的图象与性质,解二元一次方程组和一元二次方程,等腰直角三角形的性质,相似三角形的判定和性质,涉及等腰三角形的分类讨论,要充分利用等腰的性质作为列方程的依据.
7.分析:(1)二次函数表达式为:y=a(x+3)(x﹣1)=a(x2+2x﹣3),则﹣3a=﹣3,解得:a=1,即可求解;
(2)由AD2=AC2+CD2,故△ADC为直角三角形;
(3)S=PH×OA=(﹣x﹣3﹣x2﹣2x+3)=﹣(x+)2+,即可求解;
(4)分AE=EF、AE=AF、AF=EF三种情况分别求解即可.
解:(1)二次函数表达式为:y=a(x+3)(x﹣1)=a(x2+2x﹣3),
则﹣3a=﹣3,解得:a=1,
函数的表达式为:y=x2+2x﹣3;
(2)由(1)知,点D(﹣1,﹣4),
AC=3,CD=,AD==,
∴AD2=AC2+CD2,
故△ADC为直角三角形;
(3)过点P作PH∥y轴交AC于点H,
将点A、C的坐标代入一次函数表达式并解得:
直线AC的表达式为:y=﹣x﹣3,
设点P(x,x2+2x﹣3),则点H(x,﹣x﹣3),
S=PH×OA=(﹣x﹣3﹣x2﹣2x+3)=﹣(x+)2+,
当x=﹣时,S最大值为,此时点P(﹣,﹣);
(4)∵OA=OC=3,∴∠OAC=∠OCA=45°,
①当AE=EF时,如下图,
△AEF为等腰直角三角形,AE=2=EF,
∴点F(﹣1,﹣2);
②当AE=AF时,
同理可得:点F(﹣3+,﹣);
③当AF=EF时,
同理可得:点F(﹣2,﹣1);
故点F的坐标为:(﹣1,﹣2)或(﹣3+,﹣)或(﹣2,﹣1).
点评:本题考查的是二次函数综合运用,涉及到等腰三角形的性质、勾股定理的运用、面积的计算等,其中(3),要注意分类求解,避免遗漏.
8.分析:(1)用待定系数法即求得抛物线解析式;用顶点坐标公式即求得对称轴直线,得到点D坐标.
(2)求点C坐标,利用三角函数求得∠OCA的度数.由MN垂直AC可把MC转化为MN,所以当点D、M、N在同一直线上时DM+MC=DM+MN,根据垂线段最短,可知过点D作DF⊥AC于点F,此时为DM+MN最短.求∠OAC的度数,利用三角函数即求得DF的长.
(3)①求直线BC解析式,把x=1代入即求得点E坐标,进而得DE的长.由∠PDA=90°,∠PAD=60°利用三角函数求得PD的长,进而得PE的长,求得PE=2ED.
②求直线AC解析式,求点P坐标,进而求PC的长.设抛物线上的点Q坐标为(t,﹣t2﹣t+)(t≠0),根据两点间距离公式即能用t表示PQ2,CQ2.由△CPQ为等腰三角形分三种情况讨论两腰相等,即列得关于t的方程,求解得t的值即得到点Q坐标.
解:(1)∵抛物线y=ax2+bx+经过点A(1,0),B(﹣3,0)
∴ 解得:
∴抛物线的解析式为:y=﹣x2﹣x+
∵对称轴为直线:x=﹣=﹣1
∴D(﹣1,0)
(2)在M,N移动的过程中,DM+MC有最小值.
如图1,过点D作DF⊥AC于点F
∵当x=0时,y=﹣x2﹣x+=
∴C(0,)
∵A(1,0)
∴在Rt△AOC中,tan∠OCA===
∴∠OCA=30°
∵MN⊥AC,即∠MNC=90°
∴MN=MC
∴DM+MC=DM+MN
∴当点D、M、N在同一直线上时,DM+MC=DM+MN=DF最小
∵∠OAC=90°﹣∠OCA=60°
∴在Rt△DAF中,sin∠OAC=
∴DF=AD=×(1+1)=
∴DM+MC的最小值为
(3)①PE=2ED,理由如下:
设直线BC的解析式为y=kx+b
∴ 解得:
∴直线BC的解析式为y=x+,
∵对称轴为直线:x=﹣1,点E在对称轴上
∴点E(﹣1,)
∴DE=
∵∠PDA=90°,∠PAD=60°
∴在Rt△PAD中,tan∠OAC=
∴PD=2
∴PE=PD﹣DE=2﹣=
∴PE=2ED
②设直线AC解析式为y=cx+
把点A(1,0)代入得:c+=0,解得:c=﹣
∴直线AC:y=﹣x+
∵直线AC与对称轴:直线x=﹣1的交点为P
∴P(﹣1,2)
∴PC==2
∵点Q在抛物线上
∴设点Q坐标为(t,﹣t2﹣t+)(t≠0)
∴PQ2=(t+1)2+(﹣t2﹣t+﹣2)2,CQ2=t2+(﹣t2﹣t+﹣)2
i)若PQ=PC,如图2
∴PE垂直平分CQ
∴QE=CE=1,yQ=yC=
∴Q(﹣2,)
ii)若PQ=CQ,则(t+1)2+(﹣t2﹣t+﹣2)2=t2+(﹣t2﹣t+﹣)2
解得:t1=﹣2,t2=﹣1
∴Q(﹣2,)或(﹣1,)
iii)若PC=CQ,则t2+(﹣t2﹣t+﹣)2=4
解得:t=﹣2
∴Q(﹣2,)
综上所述,当△CPQ为等腰三角形时点Q的坐标分别为(﹣2,),(﹣1,).
点评:本题考查了二次函数的图象与性质,求一次函数解析式,特殊角三角函数,垂线段最短,两点间距离公式,等腰三角形的性质.求线段与线段的几分之一的和的最小值,通常需要对几分之一线段长进行转换,再利用三点共线或垂线段最短等相关定理找到最小值时的位置.
9.分析:(1)将点A、C的坐标代入抛物线,利用待定系数法求二次函数解析式解答;
(2)先求出点B的坐标,再根据三角形的面积公式求出S△ABC,设Q(m,0),表示出QA,再判断出△AQE∽△ABC,然后根据相似三角形面积的比等于相似比的平方表示出S△AQE,再根据S△QCE=S△AQC﹣S△AQE整理得到关于m的函数关系;
(3)分①当DM=DO时,DO=DM=DB=2,∠OBC=∠BMD=45°,再求出∠BDM=90°,然后写出M点的坐标;
②当MD=MO时,过点M作MN⊥OD于点N,根据等腰三角形三线合一的性质可得点N为OD的中点,求出DN=ON=1,BN=BD+DN=3,再根据△BMN为等腰直角三角形求出MN=BN=3,然后写出M点的坐标;③当OD=OM时,根据△OBC为等腰直角三角形求出点O到BC的距离,然后与OD相比较判断出不存在.
解:(1)将点A(2,0),C(0,﹣4),分别代入y=x2+bx+c,
,
解得:,
∴抛物线的解析式为y=;
(2)令y=0,即x2+x﹣4=0,解得x1=﹣4,x2=2,
∴点B(﹣4,0),
AB=2﹣(﹣4)=2+4=6,
S△ABC=AB?OC==12,
设Q点坐标为(m,0),则QA=2﹣m.
∵∠AQE=∠ABC,
∴QE∥BC,
∴△AQE∽△ABC,
∴,
∴,
S△QCE=S△AQC﹣S△AQE=,
=﹣.
(3)△OMD为等腰三角形,可能有三种情形:
①当DM=DO时,DO=DM=DA=2,
所以,∠OBC=∠BMD=45°,
所以,∠BDM=90°,
所以,M点的坐标为(﹣2,﹣2);
②当MD=MO时,如图,过点M作MN⊥OD于点N,则点N为OD的中点,
∴DN=ON=1,BN=BD+DN=3,
又△BMN为等腰直角三角形,
∴MN=BN=3,
∴M点的坐标为(﹣1,﹣3);
③当OD=OM时,
∵△OBC为等腰直角三角形,
∴点O到BC的距离为×4=2,
即BC上的点与点O之间的最小距离为2,
∵2>2,
∴OD=OM的情况不存在,
综上所述,点M的坐标为(﹣2,﹣2)或(﹣1,﹣3).
点评:本题是二次函数综合题,主要考查了待定系数法求二次函数解析式,抛物线与x轴的交点问题,三角形的面积,相似三角形面积的比等于相似比的平方的性质,等腰三角形的性质,等腰直角三角形的性质,注意等腰三角形根据腰长的不同分情况讨论.
10.分析:(1)用待定系数法即可求抛物线解析式.
(2)设点P横坐标为t,过点P作PF∥y轴交AB于点F,求直线AB解析式,即能用t表示点F坐标,进而表示PF的长.把△PAB分成△PAF与△PBF求面积和,即得到△PAB面积与t的函数关系,配方即得到t为何值时,△PAB面积最大,进而求得此时点P坐标.
(3)设点P横坐标为t,即能用t表示PD的长.根据对称性可知点P、E关于抛物线对称轴对称,用中点坐标公式可得用t表示点E横坐标,进而用t表示PE的长(注意点P、E左右位置不确定,需分类讨论).由于△PDE要成为等腰直角三角形,∠DPE=90°,所以PD=PE,把含t的式子代入求值即得到点P坐标.
解:(1)∵抛物线y=ax2+bx+3过点B(﹣3,0),C(1,0)
∴ 解得:
∴抛物线解析式为y=﹣x2﹣2x+3
(2)过点P作PH⊥x轴于点H,交AB于点F
∵x=0时,y=﹣x2﹣2x+3=3
∴A(0,3)
∴直线AB解析式为y=x+3
∵点P在线段AB上方抛物线上
∴设P(t,﹣t2﹣2t+3)(﹣3<t<0)
∴F(t,t+3)
∴PF=﹣t2﹣2t+3﹣(t+3)=﹣t2﹣3t
∴S△PAB=S△PAF+S△PBF=PF?OH+PF?BH=PF?OB=(﹣t2﹣3t)=﹣(t+)2+
∴点P运动到坐标为(﹣,),△PAB面积最大
(3)存在点P使△PDE为等腰直角三角形
设P(t,﹣t2﹣2t+3)(﹣3<t<0),则D(t,t+3)
∴PD=﹣t2﹣2t+3﹣(t+3)=﹣t2﹣3t
∵抛物线y=﹣x2﹣2x+3=﹣(x+1)2+4
∴对称轴为直线x=﹣1
∵PE∥x轴交抛物线于点E
∴yE=yP,即点E、P关于对称轴对称
∴=﹣1
∴xE=﹣2﹣xP=﹣2﹣t
∴PE=|xE﹣xP|=|﹣2﹣2t|
∵△PDE为等腰直角三角形,∠DPE=90°
∴PD=PE
①当﹣3<t≤﹣1时,PE=﹣2﹣2t
∴﹣t2﹣3t=﹣2﹣2t
解得:t1=1(舍去),t2=﹣2
∴P(﹣2,3)
②当﹣1<t<0时,PE=2+2t
∴﹣t2﹣3t=2+2t
解得:t1=,t2=(舍去)
∴P(,)
综上所述,点P坐标为(﹣2,3)或(,)时使△PDE为等腰直角三角形.
点评:本题考查了二次函数的图象与性质,求二次函数最值,等腰直角三角形的性质,中点坐标公式,一元二次方程的解法.分类讨论进行计算时,要注意讨论求得的解是否符合分类条件,是否需要舍去.
11.分析:(1)函数的表达式为:y=﹣(x+1)(x﹣5),即可求解;
(2)确定PB、CE的表达式,联立求得点F(2﹣,0),S△PCF=×PC×DF=(2﹣m)(2﹣﹣2)=5,即可求解;
(3)分当CP=CF、CP=PF、CF=PF三种情况,分别求解即可.
解:(1)函数的表达式为:y=﹣(x+1)(x﹣5)=﹣x2+x+;
(2)抛物线的对称轴为x=2,则点C(2,2),
设点P(2,m),
将点P、B的坐标代入一次函数表达式:y=sx+t并解得:
函数PB的表达式为:y=﹣mx+,
∵CE⊥PB,故直线CE表达式中的k值为,
将点C的坐标代入一次函数表达式,
同理可得直线CE的表达式为:y=,
解得:x=2﹣,
故点F(2﹣,0),
S△PCF=×PC×DF=(2﹣m)(2﹣﹣2)=5,
解得:m=5或﹣3,
故点P(2,﹣3)或(2,5);
(3)由(2)确定的点F的坐标得:
CP2=(2﹣m)2,CF2=()2+4,PF2=()2+m2,
①当CP=CF时,即:(2﹣m)2=()2+4,解得:m=0或(0舍去),
②当CP=PF时,同理可得:m=,
③当CF=PF时,同理可得:m=±2(舍去2),
故点P(2,)或(2,﹣2)或(2,)或(2,)
点评:本题考查的是二次函数综合运用,涉及到一次函数、等腰三角形性质、图形的面积计算等,其中(3),要注意分类求解,避免遗漏.
12.分析:(1)由抛物线与x轴两交点设交点式,把点D代入即求得抛物线表达式.
(2)由原抛物线顶点式可知,向下平移4个单位后顶点落在x轴上,故MN=4且MN⊥x轴.由于△AMN为等腰三角形且MN为底边,故有x轴垂直平分MN,得到点N纵坐标为﹣2,代入新抛物线解析式解方程即求得点N横坐标.
(3)作点D关于y轴的对称点D',根据轴对称性质即有QD=QD',易得当点D'、Q、E在同一直线上时,QE+QD=QE+QD'=ED'最小.由于点E随点P运动也是一个动点,由∠OEB=90°且O、B是定点可得点E的运动轨迹为圆弧.故当点E运动到点D'与圆心所连线段上时,D'E最小.求出圆心F的坐标,即求出D'F和半径r,所以D'E=D'F﹣r,所求即为QE+QD的最小值.
解:(1)抛物线与x轴交于A(﹣1,0)、B(3,0)
∴设交点式为y=a(x+1)(x﹣3)
∵抛物线经过点D(2,3)
∴a(x+1)(x﹣3)=3
解得:a=﹣1
∴抛物线表达式为y=﹣(x+1)(x﹣3)=﹣x2+2x+3
(2)∵y=﹣x2+2x+3=﹣(x﹣1)2+4
∴向下平移后新抛物线为y=﹣(x﹣1)2,顶点G(1,0),即抛物线向下平移4个单位
∵原抛物线上一点M平移后的对应点为点N
∴MN=4,MN⊥x轴
∵△AMN是以MN为底边的等腰三角形,且点A在x轴上
∴x轴垂直平分MN
∴N的纵坐标为﹣2
∴﹣(x﹣1)2=﹣2
解得:x1=1+,x2=1﹣
∴点N坐标为(1+,﹣2)或(1﹣,﹣2)
(3)作点D关于y轴的对称点点D',连接D'Q,取OB中点F,连接D'F
∵D(2,3),点Q为y轴上的动点
∴D'(﹣2,3),QD=QD'
∴当点D'、Q、E在同一直线上时,QE+QD=QE+QD'=ED'最小
∵BE⊥OP于点E,P为抛物线上第一象限内的动点
∴∠OEB=90°
∴点E在以OB为直径的圆在第一象限内的弧上运动
∵圆心F(,0),r=
∴当点E在线段D'F上时,D'E=D'F﹣EF=﹣=最小
∴QE+QD的最小值为.
点评:本题考查了二次函数的图象与性质,平移的性质,等腰三角形的性质,解一元二次方程,轴对称求最短路径,圆周角定理,勾股定理.第(3)题求线段和最小值涉及的两条线段有2个动点,先由常规的轴对称求最短路径问题确定点D'、Q、E必须共线,再找出点E运动轨迹为圆弧而得到点E在D'与圆心连线上时D'E最小.
13.分析:(1)由菱形的性质可得AD∥BC,BC=AB=10,那么∠DAB=∠CBO,根据tan∠DAB=tan∠CBO==,求出B、C、D三点的坐标,利用待定系数法求出抛物线的解析式;
(2)利用待定系数法求出直线BC的解析式为y=x+8.根据EF∥BC,可设直线EF解析式为y=x+t,根据直线EF与抛物线只有一个交点,得出方程x2+x+8=x+t只有一个解,即△=0,求出t的值,得到直线EF的解析式;
(3)分别利用当CP=CB时,△PCB为等腰三角形;当BP=BC时,△PCB为等腰三角形,利用勾股定理列方程即可.
解:(1)∵四边形ABCD是菱形,
∴AD∥BC,BC=AB=10,
∴∠DAB=∠CBO,
∴tan∠DAB=tan∠CBO==,
∵BC=10,
∴CO=8,BO=6,
∴B(﹣6,0),C(0,8),D(﹣10,8).
设抛物线的解析式为y=ax2+bx+c,
∵抛物线经过点B、C、D,
∴,解得:,
∴抛物线的解析式为y=x2+x+8;
(2)设直线BC的解析式为y=mx+n,
代入B、C点,解得:,
∴y=x+8.
∵EF∥BC,
∴设直线EF解析式为y=x+t,
又∵直线EF与抛物线只有一个交点,
∴x2+x+8=x+t只有一个解,△=0,
解得:t=5,
∴直线EF解析式为x+5;
(3)∵y=x2+x+8=(x+5)2﹣,
∴对称轴为直线x=﹣5.
设抛物线的对称轴上存在点P(﹣5,y),使△PBC是以BC为腰的等腰三角形.
B(﹣6,0),C(0,8),BC=10.
分两种情况:
①如果CP=CB,那么52+(y﹣8)2=100,解得y=8±5;
②如果BP=BC时,那么(﹣5+6)2+(y﹣0)2=100,解得y=±3.
故抛物线对称轴上存在点P,使△PBC是以BC为腰的等腰三角形,此时P点坐标为(﹣5,8+5)或(﹣5,8﹣5)或(﹣5,3)或(﹣5,﹣3).
点评:本题是二次函数综合题,涉及到利用待定系数法求函数的解析式,菱形的性质,正切函数定义,一次函数图象与几何变换,直线与抛物线的交点,等腰三角形的判定,勾股定理等知识,综合性较强,难度适中.利用方程思想与分类讨论是解题的关键
同课章节目录
