2021中考二轮复习数学《探索二次函数综合型压轴题解题技巧》分类训练三:与图形面积最值相关的压轴题(附答案)
文档属性
| 名称 | 2021中考二轮复习数学《探索二次函数综合型压轴题解题技巧》分类训练三:与图形面积最值相关的压轴题(附答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 475.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-20 00:00:00 | ||
图片预览




文档简介
2021中考数学复习《探索二次函数综合型压轴题解题技巧》分类训练三:
与图形面积最值相关的压轴题(附答案)
方法提炼:
1、三角形面积最值。分规则与不规则。有底或者高落在坐标轴上或者与坐标轴平行属于规则,直接用面积公式求解。没有底或者高落在坐标轴或平行于坐标轴属于不规则,用割补法或S△=?水平宽?铅垂高。
2、四边形面积最值。常用到的方法是利用割补法将四边形分成两个三角形(常作平行于坐标轴的直线来分割四边形面积),其求法同三角形。
典例引领:
例2:如图,抛物线y=ax2+bx+c与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴I为x=﹣1.
(1)求抛物线的解析式并写出其顶点坐标;
(2)若动点P在第二象限内的抛物线上,动点N在对称轴I上。
①当PA⊥NA,且PA=NA时,求此时点P的坐标。
②当四边形PABC的面积最大时,求四边形PABC面积的最大值及此时点P的坐标.
②方法1:
当P位于第二象限即-3<x<0时,S△AOC=,S△OCP=-x,S△OAP=?3?|yP|=-x2-3x+,
∴S△APC=S△OAP+S△OCP-S△AOC=-x2+x-9=-(x+)2+,当x=-时取得最大值;
∴当x=-时,S△APC最大值,
此时P(-,)
∵S四边PA= S△ABC+S△APC,S四边形PABC最大=.
方法2:
可求直线AC:YAC=x+3,设PD与AC的交点为E,则点E(x,x+3)
PE=-x2-2x+3-(x+3)=-x2-3x
当P位于第二象限即-3<x<0时,S△APC=?3?PE=(-x2-3x) =-(x+)2+,当x=-时取得最大值;
∴当x=-时,S△APC最大值,
此时P(-,)
∵S四边PA= S△ABC+S△APC,S四边形PABC最大=.
跟踪训练:
1.如图,已知抛物线经过两点A(﹣3,0),B(0,3),且其对称轴为直线x=﹣1.
(1)求此抛物线的解析式;
(2)直线x=m(在A、B之间)交抛物线于M点,交直线AB于N,用m表示线段MN的长.
(3)若点P是抛物线上点A与点B之间的动点(不包括点A,点B),求△PAB的面积的最大值,并求出此时点P的坐标.
2.如图,在平面直角坐标系中,抛物线y=﹣x2+4x+5与y轴交于点A,与x轴的正半轴交于点C.
(1)求直线AC解析式;
(2)过点A作AD平行于x轴,交抛物线于点D,点F为抛物线上的一点(点F在AD上方),作EF平行于y轴交AC于点E,当四边形AFDE的面积最大时?求点F的坐标,并求出最大面积;
(3)若动点P先从(2)中的点F出发沿适当的路径运动到抛物线对称轴上点M处,再沿垂直于y轴的方向运动到y轴上的点N处,然后沿适当的路径运动到点C停止,当动点P的运动路径最短时,求点N的坐标,并求最短路径长.
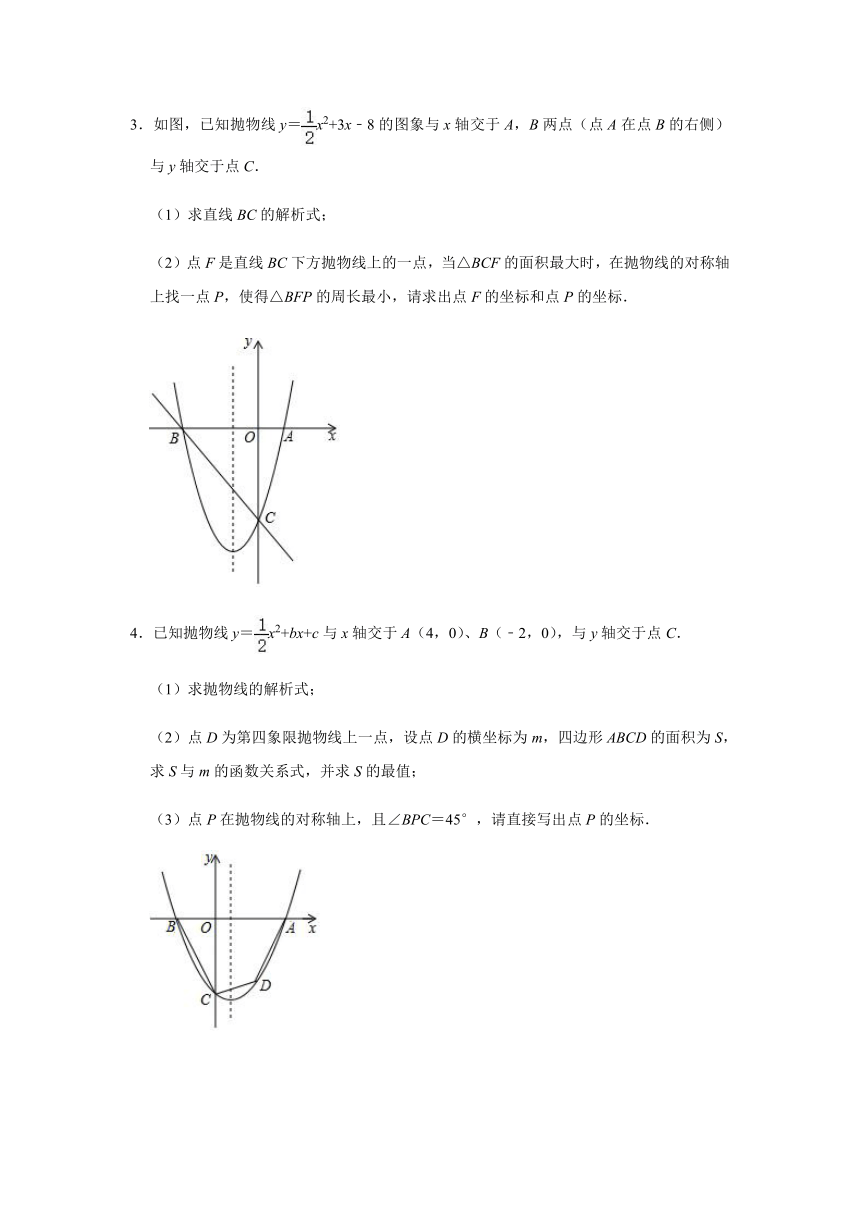
3.如图,已知抛物线y=x2+3x﹣8的图象与x轴交于A,B两点(点A在点B的右侧)与y轴交于点C.
(1)求直线BC的解析式;
(2)点F是直线BC下方抛物线上的一点,当△BCF的面积最大时,在抛物线的对称轴上找一点P,使得△BFP的周长最小,请求出点F的坐标和点P的坐标.
4.已知抛物线y=x2+bx+c与x轴交于A(4,0)、B(﹣2,0),与y轴交于点C.
(1)求抛物线的解析式;
(2)点D为第四象限抛物线上一点,设点D的横坐标为m,四边形ABCD的面积为S,求S与m的函数关系式,并求S的最值;
(3)点P在抛物线的对称轴上,且∠BPC=45°,请直接写出点P的坐标.
5.如图,直线l:y=﹣3x+8与x轴、y轴分别相交于A、B两点,抛物线y=ax2﹣2ax+a+9(a<0)经过点B.
(1)求a的值,并写出抛物线的表达式;
(2)已知点M是抛物线上的一个动点,并且点M在第一象限内,连接AM、BM,
①当点M(2,n)时,求n,并求△ABM的面积.
②当点M的横坐标为m,△ABM的面积为S,求S与m的函数表达式,并求出S的最大值和此时点M的坐标.
6.如图,已知抛物线y=﹣x2+bx+c交x轴于A(5,0),B(﹣1,0)两点,交y轴于点C.点P是线段AC上一动点.
(1)求该抛物线解析式;
(2)连接OP并延长交抛物线于点D,连接AD,是否存在点P,使S△AOP=S△APD.若存在,请求出点P坐标;若不存在,请说明理由;
(3)连结BC,过点P作PE∥CB交x轴于点E.将△CEP沿CE翻折,当点P的对应点P′恰好落在x轴上时,则E的坐标为 .
7.如图,在平面直角坐标系中,抛物线y=ax2+bx+3与x轴交于点A(3,0),B(﹣1,0),与y轴交于点C.
(1)求抛物线的解析式;
(2)点P是直线AC上方的抛物线上一动点(异于点A、C),连接BC,AC,PA,PB,PB与AC交于点D,设点P的横坐标为m.
①若△CBD,△DAP的面积分别为S1和S2,当S1﹣S2最小时,求点P的坐标;
②过点P作x轴的垂线,交AC于点E.以原点O为旋转中心,将线段PE顺时针旋转90°,得到线段P′E′.当线段P′E′与直线PE有交点时,设交点为F,求交点F的路径长.
8.如图,在平面直角坐标系中,二次函数y=x2+6x+5的图象与x轴交于A、B两点,与y轴交于点C,其顶点为P,连接PA、AC、CP,过点C作y轴的垂线l.
(1)求点P,C的坐标;
(2)直线l上是否存在点D,使△PBD的面积等于△PAC的面积的3倍?若存在,求出点D的坐标;若不存在,请说明理由.
9.如图,抛物线y=ax2+bx+6经过点A(﹣2,0),B(4,0),与y轴交于点C.点D是抛物线上的一个动点,点D的横坐标为m(1<m<4),连接AC,BC,DB,DC.
(1)求抛物线的解析式;
(2)当△BCD的面积等于△AOC的面积的时,求m的值;
(3)在抛物线的对称轴上是否存在一点Q,使得△QAC的周长最小,若存在,求出点Q的坐标.
10.如图,在平面直角坐标系中抛物线y=ax2+bx+c交x轴于点A、B,交y轴于点C,A、B两点横坐标为﹣1和3,C点纵坐标为﹣4.
(1)求抛物线的解析式;
(2)动点D在第四象限且在抛物线上,当△BCD面积最大时,求D点坐标,并求△BCD面积的最大值;
(3)抛物线的对称轴上是否存在一点Q,使得∠QBC=45°,如果存在,求出点Q的坐标,不存在说明理由.
11.综合与探究:
如图,二次函数y=ax2+bx﹣6的图象与x轴交于A,B两点,并经过点C(8,﹣6),对称轴交x轴于点D.已知点A坐标是(2,0).
(1)求点B和点D的坐标;
(2)连接并延长CD交抛物线于点E,连接BC,BE,求△EBC的面积;
(3)抛物线上有一个动点P,与A,B两点构成△ABP,是否存在S△ABP=S△DBC?若存在,请求出点P的坐标;若不存在,请说明理由.
12.如图,已知抛物线y=x2+bx+c与x轴交于点A(﹣4,0)和点B(1,0),与y轴交于点C,过点A的直线y=mx+n交抛物线的另一个点为点E,点E的横坐标为2.
(1)求b和c的值;
(2)点P在直线AE下方的抛物线上任一点,点P的横坐标为t,过点P作PF∥y轴,交AE于点F,设PF=d,求出d与t的函数关系式,并直接写出t的取值范围;
(3)在(2)问的条件下,过点P作PK⊥AE,垂足为点K,连接PE,若PF把△PKE分成面积比为11:12的两个三角形,求出此时t的值.
参考答案
1.分析:(1)抛物线经过两点A(﹣3,0),对称轴为直线x=﹣1,则抛物线与x轴另外一个交点坐标为:(1,0),即可求解;
(2)利用两点间的距离公式解答;
(3)S△PAB=PH×OA=(﹣x2﹣2x+3﹣x﹣3)×3=﹣x2﹣x,即可求解.
(1)解:∵抛物线对称轴是直线x=﹣1且经过点A(﹣3,0),
∴由抛物线的对称性可知:抛物线还经过点(1,0).
设抛物线的解析式为y=a(x﹣x1)(x﹣x2)(a≠0),即:y=a(x﹣1)(x+3).
把B(0,3)代入得:3=﹣3a.
∴a=﹣1.
∴抛物线的解析式为:y=﹣x2﹣2x+3;
(2)解:设直线AB的解析式为y=kx+b,
∵A(﹣3,0),B(0,3),
∴,
∴直线AB为y=x+3,
由题意,得M(m,﹣m2﹣2m+3),N(m,m+3)
∴MN=﹣m2﹣2m+3﹣(m+3)=﹣m2﹣3m;
(3)解:由(2)知,直线AB为y=x+3.
作PH⊥x轴于Q,交直线AB于H,
设P(x,﹣x2﹣2x+3),则H(x,x+3),
∴PH=﹣x2﹣2x+3﹣(x+3)=﹣x2﹣3x,
∴S=(﹣x2﹣3x)×3=(x+)2+,
当 x=时,S最大=,y=﹣()2﹣2×()+3=,
∴△PAB的面积的最大值为 ,此时点P的坐标为(,).
点评:考查了二次函数综合题,利用待定系数法求函数解析式的方法,利用面积的和得出二次函数是解题关键,又利用了二次函数的性质.
2.分析:(1)先求出点A,点C坐标,用待定系数法可求解析式;
(2)先求出点D坐标,设点F(x,﹣x2+4x+5),则点E坐标为(x,﹣x+5),即可求EF=﹣x2+5x,可求四边形AFDE的面积,由二次函数的性质可求解;
(3)由动点P的运动路径=FM+MN+NC=GM+2+MH,则当点G,点M,点H三点共线时,动点P的运动路径最小,由两点距离公式可求解.
解:(1)∵抛物线y=﹣x2+4x+5与y轴交于点A,与x轴的正半轴交于点C.
∴当x=0时,y=5,则点A(0,5)
当y=0时,0=﹣x2+4x+5,
∴x1=5,x2=﹣1,
∴点B(﹣1,0),点 C(5,0)
设直线AC解析式为:y=kx+b,
∴
解得:
∴直线AC解析式为:y=﹣x+5,
(2)∵过点A作AD平行于x轴,
∴点D纵坐标为5,
∴5=﹣x2+4x+5,
∴x1=0,x2=4,
∴点D(4,5),
∴AD=4
设点F(x,﹣x2+4x+5),则点E坐标为(x,﹣x+5)
∴EF=﹣x2+4x+5﹣(﹣x+5)=﹣x2+5x,
∵四边形AFDE的面积=AD×EF=2EF=﹣2x2+10x=﹣2(x﹣)2+
∴当x=时,四边形AFDE的面积的最大值为,
∴点F(,);
(3)∵抛物线y=﹣x2+4x+5=﹣(x﹣2)2+9,
∴对称轴为x=2,
∴MN=2,
如图,将点C向右平移2个单位到点H(7,0),过点F作对称轴x=2的对称点G(,),连接GH,交直线x=2于点M,
∵MN∥CH,MN=CH=2,
∴四边形MNCH是平行四边形,
∴NC=MH,
∵动点P的运动路径=FM+MN+NC=GM+2+MH,
∴当点G,点M,点H三点共线时,动点P的运动路径最小,
∴动点P的运动路径最短距离=2+=2+
设直线GH解析式为:y=mx+n,
∴
解得
∴直线GH解析式为:y=﹣x+,
当x=2时,y=,
∴点N(0,)
点评:此题是二次函数综合题,主要考查了待定系数法求解析式,函数极值的确定方法,两点距离公式等知识,解题的关键是学会利用对称解决最短问题,
3.分析:(1)利用待定系数法求出B、C两点坐标即可解决问题;
(2)如图,作FN∥y轴交BC于N.设F(m,m2+3m﹣8),则N(m,﹣m﹣8),构建二次函数,利用二次函数的性质求出点F坐标,因为点B关于对称轴的对称点是A,连接AF交对称轴于P,此时△BFP的周长最小,求出直线AF的解析式即可解决问题.
解:(1)对于抛物线y=x2+3x﹣8,
令y=0,得到x2+3x﹣8=0,解得x=﹣8或2,
∴B(﹣8,0),A(2,0),
令x=0,得到y=﹣8,
∴A(2,0),B(﹣8,0),C(0,﹣8),
设直线BC的解析式为y=kx+b,则有,
解得,
∴直线BC的解析式为y=﹣x﹣8.
(2)如图,作FN∥y轴交BC于N.设F(m,m2+3m﹣8),则N(m,﹣m﹣8)
∴S△FBC=S△FNB+S△FNC=?FN×8=4FN=4[(﹣m﹣8)﹣(m2+3m﹣8)]=﹣2m2﹣16m=﹣2(m+4)2+32,
∴当m=﹣4时,△FBC的面积有最大值,
此时F(﹣4,﹣12),
∵抛物线的对称轴x=﹣3,
点B关于对称轴的对称点是A,连接AF交对称轴于P,此时△BFP的周长最小,
设直线AF的解析式为y=ax+b(a≠0),则有,
解得,
∴直线AF的解析式为y=2x﹣4,
∴P(﹣3,﹣10),
∴点F的坐标和点P的坐标分别是F(﹣4,﹣12),P(﹣3,﹣10).
点评:本题考查二次函数综合题、一次函数的应用、待定系数法、轴对称最短问题等知识,解题的关键是学会构建二次函数,利用二次函数的性质解决问题,学会利用轴对称解决最短问题,属于中考压轴题.
4.分析:(1)抛物线的了表达式为:y=(x﹣4)(x+2)=x2﹣x﹣4;
(2)S=S△OBC+S△OCD+S△ODA=,即可求解;
(3)∠BPC=45°,则BC对应的圆心角为90°,如图作圆R,则∠BRC=90°,圆R交函数对称轴为点P,过点R作y轴的平行线交过点C与x轴的平行线于点N、交x轴于点M,证明△BMR≌△RNC(AAS),求出即点R(1,﹣1),即点R在函数对称轴上,即可求解.
解:(1)抛物线的了表达式为:y=(x﹣4)(x+2)=x2﹣x﹣4;
(2)设点D(m,m2﹣m﹣4),
S=S△OBC+S△OCD+S△ODA=AO×yD=+=[﹣(m2﹣m﹣4)]=﹣(m﹣2)2+16,
当m=2时,S的最大值为16;
(3)∠BPC=45°,则BC对应的圆心角为90°,如图作圆R,则∠BRC=90°,
圆R交函数对称轴为点P,过点R作y轴的平行线交过点C与x轴的平行线于点N、交x轴于点M,设点R(m,n).
∵∠BMR+∠MRB=90°,∠MRB+∠CRN=90°,
∴∠CRN=∠MBR,
∠BMR=∠RNC=90°,BR=RC,
∴△BMR≌△RNC(AAS),
∴CN=RM,RN=BM,
即m+2=n+4,﹣n=m,解得:m=1,n=﹣1,
即点R(1,﹣1),即点R在函数对称轴上,
圆的半径为:=,
则点P的坐标为:(1,﹣1+)或(1,﹣1﹣).
点评:本题考查的是二次函数综合运用,涉及到一次函数、圆的基本知识、图形的面积计算等,其中(3),要注意分类求解,避免遗漏.
5.分析:(1)根据题意可以求得点B的坐标,从而可以求得抛物线的解析式;
(2)根据题意可以求得点A的坐标.
①把x=2代入二次函数解析式,求得相应的y值,易得M(2,8)即n=8,所以此时MB∥x轴,根据三角形的面积公式解答即可.
②根据题意和图形可以用含m的代数式表示出S,然后将其化为顶点式,再根据二次函数的性质即可解答本题.
解:(1)把x=0代入y=﹣3x+8得y=8,
∴B(0,8).
把B(0,8)代入y=ax2﹣2ax+a+9,
∴8=a+9,
∴a=﹣1,
∴y=﹣x2+2x+8.
(2)令y=0代入得:0=﹣x2+2x+8,
∴x=﹣2或4,
∴抛物线与x轴的交点横坐标为﹣2和4.
∵M在抛物线上,且在第一象限内,
∴0<m<4,
令y=0代入y=﹣3x+8,
∴x=,
∴A的坐标为(,0).
①当x=2时,代入﹣x2+2x+8=8,则M(2,8)即n=8.
此时MB∥x轴,S△ABM=×2×8=8.
②由题意知:M的坐标为(m,﹣m2+2m+8).
S=S四边形OAMB﹣S△AOB=S△OBM+S△OAM﹣S△AOB
=×m×8+××(﹣m2+2m+8)﹣××8
=m2+m.
=
∴当m=时,S取得最大值.
当m=时,y=﹣()2+2×+8=.
∴M的坐标为(,).
点评:这是一道二次函数综合题,主要考查二次函数的最值、最短路径、待定系数法求二次函数解析式,解答本题的关键是明确题意,找出所求问题需要的条件,作出合适的辅助线,利用数形结合的思想和转化的数学思想解答.
6.分析:(1)由待定系数法可求解析式;
(2)先求出AC解析式,由S△AOP=S△APD,可得点P是OD的中点,可得P(m,(﹣m2+m+3)),代入AC解析式可求解;
(3)由勾股定理可求BC的长,由平行线的性质和折叠的性质可求BC=BE,即可求解.
解:(1)将A(5,0),B(﹣1,0)代入抛物线y=﹣x2+bx+c中,
得,
∴,
∴抛物线的解析式为y=﹣x2+x+3;
(2)由(1)知,抛物线的解析式为y=﹣x2+x+3①,
令x=0,则y=3,
∴C(0,3),
∵A(5,0),
∴直线AC的解析式为y=﹣x+3,
设点D坐标为(m,﹣m2+m+3),
∵S△AOP=S△APD.
∴点P是OD的中点,
∴P(m,(﹣m2+m+3)),
∵点P在线段AC上,
∴﹣?m+3=(﹣m2+m+3),
∴m=,
∴P(,)或(,);
(3)如图,
∵C(0,3),B(﹣1,0)
∴CO=3,BO=1,
∴BC===
∵将△CEP沿CE翻折,当点P的对应点P′恰好落在x轴上
∴∠PEC=∠BEC,
∵PE∥BC,
∴∠BCE=∠PEC,
∴∠BCE=∠BEC,
∴BC=BE=,且点B(﹣1,0)
∴E(﹣1+,0)
故答案为:E(﹣1+,0).
点评:本题是二次函数综合题,考查了待定系数法求解析式,中点坐标公式,折叠的性质,等腰三角形的性质,灵活运用这些性质进行推理是本题的关键.
7.分析:(1)抛物线的表达式为:y=a(x﹣3)(x+1)=a(x2﹣2x﹣3),即可求解;
(2)①S1﹣S2=S△BAC﹣S△BAP=×AB×(3+m2﹣2m﹣3)=2(m2﹣2m),即可求解;
②将线段PE顺时针旋转90°,得到线段P′E′,则点E′、P′的坐标分别为:(﹣m+3,﹣m)、(﹣m2+2m+3,﹣m),当线段P′E′与直线PE有交点时,即点F在E′P′之间,即可求解.
解:(1)抛物线的表达式为:y=a(x﹣3)(x+1)=a(x2﹣2x﹣3),
故﹣3a=3,解得:a=﹣1,
故抛物线的表达式为:y=﹣x2+2x+3;
(2)将点A、C(0,3)的坐标代入一次函数表达式得:
直线AC的表达式为:y=﹣x+3,
设点P(m,﹣m2+2m+3),则点E(m,﹣m+3),
①S1﹣S2=S△BAC﹣S△BAP=×AB×(3+m2﹣2m﹣3)=2(m2﹣2m),
∴当m=1时,S1﹣S2最小,此时点P(1,4);
②将线段PE顺时针旋转90°,得到线段P′E′,
则点E′、P′的坐标分别为:(﹣m+3,﹣m)、(﹣m2+2m+3,﹣m),
当线段P′E′与直线PE有交点时,即点F在E′P′之间,
即﹣m+3≤m≤﹣m2+2m+3,
解得:≤m≤,
故交点F的路径长为:(﹣)==.
点评:本题考查的是二次函数综合运用,涉及到一次函数、图形旋转、图形的面积计算等,其中(2)②,关键是求出旋转后对应点的坐标,进而求解.
8.分析:(1)利用配方法求出顶点坐标,令x=0,可得y=﹣5,推出C(0,5);
(2)直线PC的解析式为y=3x+5,设直线交x轴于E,则E(﹣,0),设直线PQ交x轴于F,当BD=3AF时,△PBD的面积等于△PAC的面积的3倍,分两种情形分别求解即可解决问题.
解:(1)∵y=x2+6x+5=(x+3)2﹣4,
∴顶点P(﹣3,﹣4).
令x=0得到y=5,
∴C(0,5);
(2)令y=0,x2+6x+5=0,解得x=﹣1或﹣5,
∴A(﹣1,0),B(﹣5,0).
设直线PC的解析式为y=kx+b,则有.
解得 .
∴直线PC的解析式y=3x+5,
设直线PC交x轴于E,则E(,0),
设直线PD交x轴于F,当BF=3AE时,△PBD的面积等于△PAC的面积的3倍,
∵AE=,
∴BF=2.
∴F(﹣3,0)或F'(﹣7,0).
当F(﹣3,0)时,直线PF垂直于x轴,
∴D(﹣3,5).
当F'(﹣7,0)时,直线PF'的解析式为y=﹣x﹣7,
∴D'(﹣12,5).
综上所述,满足条件的点D(﹣3,5),D'(﹣12,5).
点评:本题综合考查了抛物线与x轴的交点、二次函数的性质等知识,解题的关键是熟练掌握待定系数法,学会用转化的思想思考问题,属于中考常考题型.
9.分析:(1)由抛物线交点式表达,即可求解;
(2)利用S△BDC=HD×OB,即可求解;
(3)在抛物线的对称轴上存在一点Q,使得△QAC的周长最小,如图2,求得抛物线y=﹣x2+x+6的轴对称为x=1,把x=1代入直线BC的表达式y=﹣x+6即可得到结论.
解:(1)由抛物线交点式得:y=a(x+2)(x﹣4)=a(x2﹣2x﹣8)=ax2﹣2ax﹣8a,
即﹣8a=6,解得:a=﹣,
故抛物线的表达式为:y=﹣x2+x+6;
(2)点C(0,6),将点B、C的坐标代入一次函数表达式并解得:
直线BC的表达式为:y=﹣x+6,
如图所示,过点D作y轴的平行线交直线BC与点H,
设点D(m,﹣m2+m+6),则点H(m,﹣m+6)
S△BDC=HD×OB=2(﹣m2+m+6+m﹣6)=2(﹣m2+3m)=S△ACO=××6×2=,
即:2(﹣m2+3m)=,
解得:m=1或3(舍去1),
故m=3;
(3)在抛物线的对称轴上存在一点Q,使得△QAC的周长最小,如图2,
抛物线y=﹣x2+x+6的轴对称与BC 的交点即为点Q,
∵抛物线y=﹣x2+x+6的轴对称为x=1,
∴把x=1代入直线BC的表达式y=﹣x+6得y=,
∴点Q的坐标为(1,).
点评:本题考查的是二次函数综合运用,待定系数法求函数的解析式,图象的面积计算,轴对称﹣最短路线问题等,正确理解题意是解题的关键.
10.分析:(1)抛物线的表达式为:y=a(x+1)(x﹣3)=a(x2﹣2x﹣3),即可求解;
(2)S△BCD=×OB×ND=3×(x﹣4﹣x2+x+4)=﹣2x2+6x,即可求解;
(3)设QM=3x,则HM=4x,MB=3x,BH=HM+MB=7x==,解得:x=,即可求解.
解:(1)抛物线的表达式为:y=a(x+1)(x﹣3)=a(x2﹣2x﹣3),
故﹣3a=﹣4,解得:a=,
故抛物线的表达式为:y=x2﹣x﹣4;
(2)过点D作y轴的平行线交BC于点N,
由B、C的坐标可得直线BC的表达式为:y=x﹣4,
设点D(x,x2﹣x﹣4),点N(x,x﹣4),
S△BCD=×OB×ND=3×(x﹣4﹣x2+x+4)=﹣2x2+6x,
∵﹣2<0,故S有最大值,
此时,x=,点D(,﹣5);
(3)存在,理由:
直线BC的表达式为:y=x﹣4,抛物线的对称轴为:x=1,故点H(1,﹣),
过点Q作QM⊥BC于点M,tan∠OCB==tanα,∠QBC=45°,
设QM=3x,则HM=4x,MB=3x,
BH=HM+MB=7x==,解得:x=,
QH=5x=,
则yQ=yH+=﹣,
故点Q(1,).
点评:本题考查的是二次函数综合运用,涉及到一次函数、解直角三角形、图形的面积计算等,其中(3),用解直角三角形的方法求解点Q的坐标,是本题的亮点.
11.分析:(1)利用待定系数法求出抛物线解析式,进而求出抛物线对称轴,求出点D的坐标,再令y=0,进而求出点B坐标;
(2)先利用待定系数法求出直线CD的解析式,进而求出点E的坐标,再求出点F的坐标,即可得出结论;
(3)先求出△DBC的面积,进而求出△ABP,求出点P的纵坐标,即可得出结论.
解:(1)二次函数y=ax2+bx﹣6的图象经过点C(8,﹣6),点A(2,0),
∴,
∴,
∴二次函数的解析式为y=﹣x2+4x﹣6,
∴抛物线的对称轴为x=﹣=4,
∴D(4,0);
当y=0时,则﹣x2+4x﹣6=0,
∴x=2(点A的横坐标)或x=6,
∴B(6,0);
(2)由(1)知,D(4,0),
∵C(8,﹣6),
∴直线CD的解析式为y=﹣x+6①,
由(1)知,二次函数的解析式为y=﹣x2+4x﹣6②,
联立①②解得,或(点C的纵横坐标),
∴点E(3,),
如图1,过点B作BF∥y轴交CD于F,
由(1)知,B(6,0),
∴F(6,﹣3),
∴S△EBC=BF?|xC﹣xE|=×3×|8﹣3|=;
(3)设点P的纵坐标为m,由(1)知,B(6,0),D(4,0),
∵C(8,﹣6),
∴S△DBC=BD?|yC|=(6﹣4)×6=6,
∵S△ABP=S△DBC,
∴S△ABP=×6=3,
∵A(2,0),B(6,0),
∴S△ABP=AB?|yP|=(6﹣2)|m|=2|m|=3,
∴m=±,
当m=时,﹣x2+4x﹣6=,x=3或x=5,
∴P(3,)或(5,),
当m=﹣时,﹣x2+4x﹣6=﹣,x=4﹣或x=4+,
∴P(4﹣,﹣)或(4+,﹣),即:P(3,)或(5,)或(4﹣,﹣)或(4+,﹣).
点评:此题是二次函数综合题,主要考查了待定系数法,三角形面积的求法,用方程的思想解决问题是解本题的关键.
12.分析:(1)抛物线的表达式为:y=(x+4)(x﹣1),即可求解;
(2)直线AE的表达式为:y=x+2,点P(t,t2+t﹣2),则点F(t,t+2),d=PF=t+2﹣(t2+t﹣2)=﹣t2﹣t+4(﹣4<t<2);
(3)PF把△PKE分成面积比为11:12的两个三角形,则ER:KH=12:11,即:(2﹣t):(t﹣xK)=12:11,解得:xK=,则点K(,),直线PK的表达式为:y=﹣2x+,将点P的坐标代入上式并化简得:12t2﹣31t+14=0,即可求解.
解:(1)抛物线的表达式为:y=(x+4)(x﹣1)=x2+x﹣2,
则b=,c=﹣2;
(2)点E的横坐标为2,而点E在抛物线上,则点E(2,3),
将A、E的坐标代入y=mx+n得:,解得:,
故直线AE的表达式为:y=x+2,
点P(t,t2+t﹣2),则点F(t,t+2),
d=PF=t+2﹣(t2+t﹣2)=﹣t2﹣t+4(﹣4<t<2);
(3)点P(t,t2+t﹣2),分别过点E、K作PF的垂线交于点R、H,
PF把△PKE分成面积比为11:12的两个三角形,当ER:KH=12:11时,
即:(2﹣t):(t﹣xK)=12:11,
解得:xK=,
则yK=,点K在直线AE上,则点K(,),
∵PK⊥AE,则直线PK的表达式可设为:y=﹣2x+s,
将点K的坐标代入上式并解得:
直线PK的表达式为:y=﹣2x+,
将点P的坐标代入上式并化简得:12t2﹣31t+14=0,
解得:t=或2(舍去2);
PF把△PKE分成面积比为11:12的两个三角形,当ER:KH=11:12时,
同理可得:t=;
综上,t=或
与图形面积最值相关的压轴题(附答案)
方法提炼:
1、三角形面积最值。分规则与不规则。有底或者高落在坐标轴上或者与坐标轴平行属于规则,直接用面积公式求解。没有底或者高落在坐标轴或平行于坐标轴属于不规则,用割补法或S△=?水平宽?铅垂高。
2、四边形面积最值。常用到的方法是利用割补法将四边形分成两个三角形(常作平行于坐标轴的直线来分割四边形面积),其求法同三角形。
典例引领:
例2:如图,抛物线y=ax2+bx+c与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴I为x=﹣1.
(1)求抛物线的解析式并写出其顶点坐标;
(2)若动点P在第二象限内的抛物线上,动点N在对称轴I上。
①当PA⊥NA,且PA=NA时,求此时点P的坐标。
②当四边形PABC的面积最大时,求四边形PABC面积的最大值及此时点P的坐标.
②方法1:
当P位于第二象限即-3<x<0时,S△AOC=,S△OCP=-x,S△OAP=?3?|yP|=-x2-3x+,
∴S△APC=S△OAP+S△OCP-S△AOC=-x2+x-9=-(x+)2+,当x=-时取得最大值;
∴当x=-时,S△APC最大值,
此时P(-,)
∵S四边PA= S△ABC+S△APC,S四边形PABC最大=.
方法2:
可求直线AC:YAC=x+3,设PD与AC的交点为E,则点E(x,x+3)
PE=-x2-2x+3-(x+3)=-x2-3x
当P位于第二象限即-3<x<0时,S△APC=?3?PE=(-x2-3x) =-(x+)2+,当x=-时取得最大值;
∴当x=-时,S△APC最大值,
此时P(-,)
∵S四边PA= S△ABC+S△APC,S四边形PABC最大=.
跟踪训练:
1.如图,已知抛物线经过两点A(﹣3,0),B(0,3),且其对称轴为直线x=﹣1.
(1)求此抛物线的解析式;
(2)直线x=m(在A、B之间)交抛物线于M点,交直线AB于N,用m表示线段MN的长.
(3)若点P是抛物线上点A与点B之间的动点(不包括点A,点B),求△PAB的面积的最大值,并求出此时点P的坐标.
2.如图,在平面直角坐标系中,抛物线y=﹣x2+4x+5与y轴交于点A,与x轴的正半轴交于点C.
(1)求直线AC解析式;
(2)过点A作AD平行于x轴,交抛物线于点D,点F为抛物线上的一点(点F在AD上方),作EF平行于y轴交AC于点E,当四边形AFDE的面积最大时?求点F的坐标,并求出最大面积;
(3)若动点P先从(2)中的点F出发沿适当的路径运动到抛物线对称轴上点M处,再沿垂直于y轴的方向运动到y轴上的点N处,然后沿适当的路径运动到点C停止,当动点P的运动路径最短时,求点N的坐标,并求最短路径长.
3.如图,已知抛物线y=x2+3x﹣8的图象与x轴交于A,B两点(点A在点B的右侧)与y轴交于点C.
(1)求直线BC的解析式;
(2)点F是直线BC下方抛物线上的一点,当△BCF的面积最大时,在抛物线的对称轴上找一点P,使得△BFP的周长最小,请求出点F的坐标和点P的坐标.
4.已知抛物线y=x2+bx+c与x轴交于A(4,0)、B(﹣2,0),与y轴交于点C.
(1)求抛物线的解析式;
(2)点D为第四象限抛物线上一点,设点D的横坐标为m,四边形ABCD的面积为S,求S与m的函数关系式,并求S的最值;
(3)点P在抛物线的对称轴上,且∠BPC=45°,请直接写出点P的坐标.
5.如图,直线l:y=﹣3x+8与x轴、y轴分别相交于A、B两点,抛物线y=ax2﹣2ax+a+9(a<0)经过点B.
(1)求a的值,并写出抛物线的表达式;
(2)已知点M是抛物线上的一个动点,并且点M在第一象限内,连接AM、BM,
①当点M(2,n)时,求n,并求△ABM的面积.
②当点M的横坐标为m,△ABM的面积为S,求S与m的函数表达式,并求出S的最大值和此时点M的坐标.
6.如图,已知抛物线y=﹣x2+bx+c交x轴于A(5,0),B(﹣1,0)两点,交y轴于点C.点P是线段AC上一动点.
(1)求该抛物线解析式;
(2)连接OP并延长交抛物线于点D,连接AD,是否存在点P,使S△AOP=S△APD.若存在,请求出点P坐标;若不存在,请说明理由;
(3)连结BC,过点P作PE∥CB交x轴于点E.将△CEP沿CE翻折,当点P的对应点P′恰好落在x轴上时,则E的坐标为 .
7.如图,在平面直角坐标系中,抛物线y=ax2+bx+3与x轴交于点A(3,0),B(﹣1,0),与y轴交于点C.
(1)求抛物线的解析式;
(2)点P是直线AC上方的抛物线上一动点(异于点A、C),连接BC,AC,PA,PB,PB与AC交于点D,设点P的横坐标为m.
①若△CBD,△DAP的面积分别为S1和S2,当S1﹣S2最小时,求点P的坐标;
②过点P作x轴的垂线,交AC于点E.以原点O为旋转中心,将线段PE顺时针旋转90°,得到线段P′E′.当线段P′E′与直线PE有交点时,设交点为F,求交点F的路径长.
8.如图,在平面直角坐标系中,二次函数y=x2+6x+5的图象与x轴交于A、B两点,与y轴交于点C,其顶点为P,连接PA、AC、CP,过点C作y轴的垂线l.
(1)求点P,C的坐标;
(2)直线l上是否存在点D,使△PBD的面积等于△PAC的面积的3倍?若存在,求出点D的坐标;若不存在,请说明理由.
9.如图,抛物线y=ax2+bx+6经过点A(﹣2,0),B(4,0),与y轴交于点C.点D是抛物线上的一个动点,点D的横坐标为m(1<m<4),连接AC,BC,DB,DC.
(1)求抛物线的解析式;
(2)当△BCD的面积等于△AOC的面积的时,求m的值;
(3)在抛物线的对称轴上是否存在一点Q,使得△QAC的周长最小,若存在,求出点Q的坐标.
10.如图,在平面直角坐标系中抛物线y=ax2+bx+c交x轴于点A、B,交y轴于点C,A、B两点横坐标为﹣1和3,C点纵坐标为﹣4.
(1)求抛物线的解析式;
(2)动点D在第四象限且在抛物线上,当△BCD面积最大时,求D点坐标,并求△BCD面积的最大值;
(3)抛物线的对称轴上是否存在一点Q,使得∠QBC=45°,如果存在,求出点Q的坐标,不存在说明理由.
11.综合与探究:
如图,二次函数y=ax2+bx﹣6的图象与x轴交于A,B两点,并经过点C(8,﹣6),对称轴交x轴于点D.已知点A坐标是(2,0).
(1)求点B和点D的坐标;
(2)连接并延长CD交抛物线于点E,连接BC,BE,求△EBC的面积;
(3)抛物线上有一个动点P,与A,B两点构成△ABP,是否存在S△ABP=S△DBC?若存在,请求出点P的坐标;若不存在,请说明理由.
12.如图,已知抛物线y=x2+bx+c与x轴交于点A(﹣4,0)和点B(1,0),与y轴交于点C,过点A的直线y=mx+n交抛物线的另一个点为点E,点E的横坐标为2.
(1)求b和c的值;
(2)点P在直线AE下方的抛物线上任一点,点P的横坐标为t,过点P作PF∥y轴,交AE于点F,设PF=d,求出d与t的函数关系式,并直接写出t的取值范围;
(3)在(2)问的条件下,过点P作PK⊥AE,垂足为点K,连接PE,若PF把△PKE分成面积比为11:12的两个三角形,求出此时t的值.
参考答案
1.分析:(1)抛物线经过两点A(﹣3,0),对称轴为直线x=﹣1,则抛物线与x轴另外一个交点坐标为:(1,0),即可求解;
(2)利用两点间的距离公式解答;
(3)S△PAB=PH×OA=(﹣x2﹣2x+3﹣x﹣3)×3=﹣x2﹣x,即可求解.
(1)解:∵抛物线对称轴是直线x=﹣1且经过点A(﹣3,0),
∴由抛物线的对称性可知:抛物线还经过点(1,0).
设抛物线的解析式为y=a(x﹣x1)(x﹣x2)(a≠0),即:y=a(x﹣1)(x+3).
把B(0,3)代入得:3=﹣3a.
∴a=﹣1.
∴抛物线的解析式为:y=﹣x2﹣2x+3;
(2)解:设直线AB的解析式为y=kx+b,
∵A(﹣3,0),B(0,3),
∴,
∴直线AB为y=x+3,
由题意,得M(m,﹣m2﹣2m+3),N(m,m+3)
∴MN=﹣m2﹣2m+3﹣(m+3)=﹣m2﹣3m;
(3)解:由(2)知,直线AB为y=x+3.
作PH⊥x轴于Q,交直线AB于H,
设P(x,﹣x2﹣2x+3),则H(x,x+3),
∴PH=﹣x2﹣2x+3﹣(x+3)=﹣x2﹣3x,
∴S=(﹣x2﹣3x)×3=(x+)2+,
当 x=时,S最大=,y=﹣()2﹣2×()+3=,
∴△PAB的面积的最大值为 ,此时点P的坐标为(,).
点评:考查了二次函数综合题,利用待定系数法求函数解析式的方法,利用面积的和得出二次函数是解题关键,又利用了二次函数的性质.
2.分析:(1)先求出点A,点C坐标,用待定系数法可求解析式;
(2)先求出点D坐标,设点F(x,﹣x2+4x+5),则点E坐标为(x,﹣x+5),即可求EF=﹣x2+5x,可求四边形AFDE的面积,由二次函数的性质可求解;
(3)由动点P的运动路径=FM+MN+NC=GM+2+MH,则当点G,点M,点H三点共线时,动点P的运动路径最小,由两点距离公式可求解.
解:(1)∵抛物线y=﹣x2+4x+5与y轴交于点A,与x轴的正半轴交于点C.
∴当x=0时,y=5,则点A(0,5)
当y=0时,0=﹣x2+4x+5,
∴x1=5,x2=﹣1,
∴点B(﹣1,0),点 C(5,0)
设直线AC解析式为:y=kx+b,
∴
解得:
∴直线AC解析式为:y=﹣x+5,
(2)∵过点A作AD平行于x轴,
∴点D纵坐标为5,
∴5=﹣x2+4x+5,
∴x1=0,x2=4,
∴点D(4,5),
∴AD=4
设点F(x,﹣x2+4x+5),则点E坐标为(x,﹣x+5)
∴EF=﹣x2+4x+5﹣(﹣x+5)=﹣x2+5x,
∵四边形AFDE的面积=AD×EF=2EF=﹣2x2+10x=﹣2(x﹣)2+
∴当x=时,四边形AFDE的面积的最大值为,
∴点F(,);
(3)∵抛物线y=﹣x2+4x+5=﹣(x﹣2)2+9,
∴对称轴为x=2,
∴MN=2,
如图,将点C向右平移2个单位到点H(7,0),过点F作对称轴x=2的对称点G(,),连接GH,交直线x=2于点M,
∵MN∥CH,MN=CH=2,
∴四边形MNCH是平行四边形,
∴NC=MH,
∵动点P的运动路径=FM+MN+NC=GM+2+MH,
∴当点G,点M,点H三点共线时,动点P的运动路径最小,
∴动点P的运动路径最短距离=2+=2+
设直线GH解析式为:y=mx+n,
∴
解得
∴直线GH解析式为:y=﹣x+,
当x=2时,y=,
∴点N(0,)
点评:此题是二次函数综合题,主要考查了待定系数法求解析式,函数极值的确定方法,两点距离公式等知识,解题的关键是学会利用对称解决最短问题,
3.分析:(1)利用待定系数法求出B、C两点坐标即可解决问题;
(2)如图,作FN∥y轴交BC于N.设F(m,m2+3m﹣8),则N(m,﹣m﹣8),构建二次函数,利用二次函数的性质求出点F坐标,因为点B关于对称轴的对称点是A,连接AF交对称轴于P,此时△BFP的周长最小,求出直线AF的解析式即可解决问题.
解:(1)对于抛物线y=x2+3x﹣8,
令y=0,得到x2+3x﹣8=0,解得x=﹣8或2,
∴B(﹣8,0),A(2,0),
令x=0,得到y=﹣8,
∴A(2,0),B(﹣8,0),C(0,﹣8),
设直线BC的解析式为y=kx+b,则有,
解得,
∴直线BC的解析式为y=﹣x﹣8.
(2)如图,作FN∥y轴交BC于N.设F(m,m2+3m﹣8),则N(m,﹣m﹣8)
∴S△FBC=S△FNB+S△FNC=?FN×8=4FN=4[(﹣m﹣8)﹣(m2+3m﹣8)]=﹣2m2﹣16m=﹣2(m+4)2+32,
∴当m=﹣4时,△FBC的面积有最大值,
此时F(﹣4,﹣12),
∵抛物线的对称轴x=﹣3,
点B关于对称轴的对称点是A,连接AF交对称轴于P,此时△BFP的周长最小,
设直线AF的解析式为y=ax+b(a≠0),则有,
解得,
∴直线AF的解析式为y=2x﹣4,
∴P(﹣3,﹣10),
∴点F的坐标和点P的坐标分别是F(﹣4,﹣12),P(﹣3,﹣10).
点评:本题考查二次函数综合题、一次函数的应用、待定系数法、轴对称最短问题等知识,解题的关键是学会构建二次函数,利用二次函数的性质解决问题,学会利用轴对称解决最短问题,属于中考压轴题.
4.分析:(1)抛物线的了表达式为:y=(x﹣4)(x+2)=x2﹣x﹣4;
(2)S=S△OBC+S△OCD+S△ODA=,即可求解;
(3)∠BPC=45°,则BC对应的圆心角为90°,如图作圆R,则∠BRC=90°,圆R交函数对称轴为点P,过点R作y轴的平行线交过点C与x轴的平行线于点N、交x轴于点M,证明△BMR≌△RNC(AAS),求出即点R(1,﹣1),即点R在函数对称轴上,即可求解.
解:(1)抛物线的了表达式为:y=(x﹣4)(x+2)=x2﹣x﹣4;
(2)设点D(m,m2﹣m﹣4),
S=S△OBC+S△OCD+S△ODA=AO×yD=+=[﹣(m2﹣m﹣4)]=﹣(m﹣2)2+16,
当m=2时,S的最大值为16;
(3)∠BPC=45°,则BC对应的圆心角为90°,如图作圆R,则∠BRC=90°,
圆R交函数对称轴为点P,过点R作y轴的平行线交过点C与x轴的平行线于点N、交x轴于点M,设点R(m,n).
∵∠BMR+∠MRB=90°,∠MRB+∠CRN=90°,
∴∠CRN=∠MBR,
∠BMR=∠RNC=90°,BR=RC,
∴△BMR≌△RNC(AAS),
∴CN=RM,RN=BM,
即m+2=n+4,﹣n=m,解得:m=1,n=﹣1,
即点R(1,﹣1),即点R在函数对称轴上,
圆的半径为:=,
则点P的坐标为:(1,﹣1+)或(1,﹣1﹣).
点评:本题考查的是二次函数综合运用,涉及到一次函数、圆的基本知识、图形的面积计算等,其中(3),要注意分类求解,避免遗漏.
5.分析:(1)根据题意可以求得点B的坐标,从而可以求得抛物线的解析式;
(2)根据题意可以求得点A的坐标.
①把x=2代入二次函数解析式,求得相应的y值,易得M(2,8)即n=8,所以此时MB∥x轴,根据三角形的面积公式解答即可.
②根据题意和图形可以用含m的代数式表示出S,然后将其化为顶点式,再根据二次函数的性质即可解答本题.
解:(1)把x=0代入y=﹣3x+8得y=8,
∴B(0,8).
把B(0,8)代入y=ax2﹣2ax+a+9,
∴8=a+9,
∴a=﹣1,
∴y=﹣x2+2x+8.
(2)令y=0代入得:0=﹣x2+2x+8,
∴x=﹣2或4,
∴抛物线与x轴的交点横坐标为﹣2和4.
∵M在抛物线上,且在第一象限内,
∴0<m<4,
令y=0代入y=﹣3x+8,
∴x=,
∴A的坐标为(,0).
①当x=2时,代入﹣x2+2x+8=8,则M(2,8)即n=8.
此时MB∥x轴,S△ABM=×2×8=8.
②由题意知:M的坐标为(m,﹣m2+2m+8).
S=S四边形OAMB﹣S△AOB=S△OBM+S△OAM﹣S△AOB
=×m×8+××(﹣m2+2m+8)﹣××8
=m2+m.
=
∴当m=时,S取得最大值.
当m=时,y=﹣()2+2×+8=.
∴M的坐标为(,).
点评:这是一道二次函数综合题,主要考查二次函数的最值、最短路径、待定系数法求二次函数解析式,解答本题的关键是明确题意,找出所求问题需要的条件,作出合适的辅助线,利用数形结合的思想和转化的数学思想解答.
6.分析:(1)由待定系数法可求解析式;
(2)先求出AC解析式,由S△AOP=S△APD,可得点P是OD的中点,可得P(m,(﹣m2+m+3)),代入AC解析式可求解;
(3)由勾股定理可求BC的长,由平行线的性质和折叠的性质可求BC=BE,即可求解.
解:(1)将A(5,0),B(﹣1,0)代入抛物线y=﹣x2+bx+c中,
得,
∴,
∴抛物线的解析式为y=﹣x2+x+3;
(2)由(1)知,抛物线的解析式为y=﹣x2+x+3①,
令x=0,则y=3,
∴C(0,3),
∵A(5,0),
∴直线AC的解析式为y=﹣x+3,
设点D坐标为(m,﹣m2+m+3),
∵S△AOP=S△APD.
∴点P是OD的中点,
∴P(m,(﹣m2+m+3)),
∵点P在线段AC上,
∴﹣?m+3=(﹣m2+m+3),
∴m=,
∴P(,)或(,);
(3)如图,
∵C(0,3),B(﹣1,0)
∴CO=3,BO=1,
∴BC===
∵将△CEP沿CE翻折,当点P的对应点P′恰好落在x轴上
∴∠PEC=∠BEC,
∵PE∥BC,
∴∠BCE=∠PEC,
∴∠BCE=∠BEC,
∴BC=BE=,且点B(﹣1,0)
∴E(﹣1+,0)
故答案为:E(﹣1+,0).
点评:本题是二次函数综合题,考查了待定系数法求解析式,中点坐标公式,折叠的性质,等腰三角形的性质,灵活运用这些性质进行推理是本题的关键.
7.分析:(1)抛物线的表达式为:y=a(x﹣3)(x+1)=a(x2﹣2x﹣3),即可求解;
(2)①S1﹣S2=S△BAC﹣S△BAP=×AB×(3+m2﹣2m﹣3)=2(m2﹣2m),即可求解;
②将线段PE顺时针旋转90°,得到线段P′E′,则点E′、P′的坐标分别为:(﹣m+3,﹣m)、(﹣m2+2m+3,﹣m),当线段P′E′与直线PE有交点时,即点F在E′P′之间,即可求解.
解:(1)抛物线的表达式为:y=a(x﹣3)(x+1)=a(x2﹣2x﹣3),
故﹣3a=3,解得:a=﹣1,
故抛物线的表达式为:y=﹣x2+2x+3;
(2)将点A、C(0,3)的坐标代入一次函数表达式得:
直线AC的表达式为:y=﹣x+3,
设点P(m,﹣m2+2m+3),则点E(m,﹣m+3),
①S1﹣S2=S△BAC﹣S△BAP=×AB×(3+m2﹣2m﹣3)=2(m2﹣2m),
∴当m=1时,S1﹣S2最小,此时点P(1,4);
②将线段PE顺时针旋转90°,得到线段P′E′,
则点E′、P′的坐标分别为:(﹣m+3,﹣m)、(﹣m2+2m+3,﹣m),
当线段P′E′与直线PE有交点时,即点F在E′P′之间,
即﹣m+3≤m≤﹣m2+2m+3,
解得:≤m≤,
故交点F的路径长为:(﹣)==.
点评:本题考查的是二次函数综合运用,涉及到一次函数、图形旋转、图形的面积计算等,其中(2)②,关键是求出旋转后对应点的坐标,进而求解.
8.分析:(1)利用配方法求出顶点坐标,令x=0,可得y=﹣5,推出C(0,5);
(2)直线PC的解析式为y=3x+5,设直线交x轴于E,则E(﹣,0),设直线PQ交x轴于F,当BD=3AF时,△PBD的面积等于△PAC的面积的3倍,分两种情形分别求解即可解决问题.
解:(1)∵y=x2+6x+5=(x+3)2﹣4,
∴顶点P(﹣3,﹣4).
令x=0得到y=5,
∴C(0,5);
(2)令y=0,x2+6x+5=0,解得x=﹣1或﹣5,
∴A(﹣1,0),B(﹣5,0).
设直线PC的解析式为y=kx+b,则有.
解得 .
∴直线PC的解析式y=3x+5,
设直线PC交x轴于E,则E(,0),
设直线PD交x轴于F,当BF=3AE时,△PBD的面积等于△PAC的面积的3倍,
∵AE=,
∴BF=2.
∴F(﹣3,0)或F'(﹣7,0).
当F(﹣3,0)时,直线PF垂直于x轴,
∴D(﹣3,5).
当F'(﹣7,0)时,直线PF'的解析式为y=﹣x﹣7,
∴D'(﹣12,5).
综上所述,满足条件的点D(﹣3,5),D'(﹣12,5).
点评:本题综合考查了抛物线与x轴的交点、二次函数的性质等知识,解题的关键是熟练掌握待定系数法,学会用转化的思想思考问题,属于中考常考题型.
9.分析:(1)由抛物线交点式表达,即可求解;
(2)利用S△BDC=HD×OB,即可求解;
(3)在抛物线的对称轴上存在一点Q,使得△QAC的周长最小,如图2,求得抛物线y=﹣x2+x+6的轴对称为x=1,把x=1代入直线BC的表达式y=﹣x+6即可得到结论.
解:(1)由抛物线交点式得:y=a(x+2)(x﹣4)=a(x2﹣2x﹣8)=ax2﹣2ax﹣8a,
即﹣8a=6,解得:a=﹣,
故抛物线的表达式为:y=﹣x2+x+6;
(2)点C(0,6),将点B、C的坐标代入一次函数表达式并解得:
直线BC的表达式为:y=﹣x+6,
如图所示,过点D作y轴的平行线交直线BC与点H,
设点D(m,﹣m2+m+6),则点H(m,﹣m+6)
S△BDC=HD×OB=2(﹣m2+m+6+m﹣6)=2(﹣m2+3m)=S△ACO=××6×2=,
即:2(﹣m2+3m)=,
解得:m=1或3(舍去1),
故m=3;
(3)在抛物线的对称轴上存在一点Q,使得△QAC的周长最小,如图2,
抛物线y=﹣x2+x+6的轴对称与BC 的交点即为点Q,
∵抛物线y=﹣x2+x+6的轴对称为x=1,
∴把x=1代入直线BC的表达式y=﹣x+6得y=,
∴点Q的坐标为(1,).
点评:本题考查的是二次函数综合运用,待定系数法求函数的解析式,图象的面积计算,轴对称﹣最短路线问题等,正确理解题意是解题的关键.
10.分析:(1)抛物线的表达式为:y=a(x+1)(x﹣3)=a(x2﹣2x﹣3),即可求解;
(2)S△BCD=×OB×ND=3×(x﹣4﹣x2+x+4)=﹣2x2+6x,即可求解;
(3)设QM=3x,则HM=4x,MB=3x,BH=HM+MB=7x==,解得:x=,即可求解.
解:(1)抛物线的表达式为:y=a(x+1)(x﹣3)=a(x2﹣2x﹣3),
故﹣3a=﹣4,解得:a=,
故抛物线的表达式为:y=x2﹣x﹣4;
(2)过点D作y轴的平行线交BC于点N,
由B、C的坐标可得直线BC的表达式为:y=x﹣4,
设点D(x,x2﹣x﹣4),点N(x,x﹣4),
S△BCD=×OB×ND=3×(x﹣4﹣x2+x+4)=﹣2x2+6x,
∵﹣2<0,故S有最大值,
此时,x=,点D(,﹣5);
(3)存在,理由:
直线BC的表达式为:y=x﹣4,抛物线的对称轴为:x=1,故点H(1,﹣),
过点Q作QM⊥BC于点M,tan∠OCB==tanα,∠QBC=45°,
设QM=3x,则HM=4x,MB=3x,
BH=HM+MB=7x==,解得:x=,
QH=5x=,
则yQ=yH+=﹣,
故点Q(1,).
点评:本题考查的是二次函数综合运用,涉及到一次函数、解直角三角形、图形的面积计算等,其中(3),用解直角三角形的方法求解点Q的坐标,是本题的亮点.
11.分析:(1)利用待定系数法求出抛物线解析式,进而求出抛物线对称轴,求出点D的坐标,再令y=0,进而求出点B坐标;
(2)先利用待定系数法求出直线CD的解析式,进而求出点E的坐标,再求出点F的坐标,即可得出结论;
(3)先求出△DBC的面积,进而求出△ABP,求出点P的纵坐标,即可得出结论.
解:(1)二次函数y=ax2+bx﹣6的图象经过点C(8,﹣6),点A(2,0),
∴,
∴,
∴二次函数的解析式为y=﹣x2+4x﹣6,
∴抛物线的对称轴为x=﹣=4,
∴D(4,0);
当y=0时,则﹣x2+4x﹣6=0,
∴x=2(点A的横坐标)或x=6,
∴B(6,0);
(2)由(1)知,D(4,0),
∵C(8,﹣6),
∴直线CD的解析式为y=﹣x+6①,
由(1)知,二次函数的解析式为y=﹣x2+4x﹣6②,
联立①②解得,或(点C的纵横坐标),
∴点E(3,),
如图1,过点B作BF∥y轴交CD于F,
由(1)知,B(6,0),
∴F(6,﹣3),
∴S△EBC=BF?|xC﹣xE|=×3×|8﹣3|=;
(3)设点P的纵坐标为m,由(1)知,B(6,0),D(4,0),
∵C(8,﹣6),
∴S△DBC=BD?|yC|=(6﹣4)×6=6,
∵S△ABP=S△DBC,
∴S△ABP=×6=3,
∵A(2,0),B(6,0),
∴S△ABP=AB?|yP|=(6﹣2)|m|=2|m|=3,
∴m=±,
当m=时,﹣x2+4x﹣6=,x=3或x=5,
∴P(3,)或(5,),
当m=﹣时,﹣x2+4x﹣6=﹣,x=4﹣或x=4+,
∴P(4﹣,﹣)或(4+,﹣),即:P(3,)或(5,)或(4﹣,﹣)或(4+,﹣).
点评:此题是二次函数综合题,主要考查了待定系数法,三角形面积的求法,用方程的思想解决问题是解本题的关键.
12.分析:(1)抛物线的表达式为:y=(x+4)(x﹣1),即可求解;
(2)直线AE的表达式为:y=x+2,点P(t,t2+t﹣2),则点F(t,t+2),d=PF=t+2﹣(t2+t﹣2)=﹣t2﹣t+4(﹣4<t<2);
(3)PF把△PKE分成面积比为11:12的两个三角形,则ER:KH=12:11,即:(2﹣t):(t﹣xK)=12:11,解得:xK=,则点K(,),直线PK的表达式为:y=﹣2x+,将点P的坐标代入上式并化简得:12t2﹣31t+14=0,即可求解.
解:(1)抛物线的表达式为:y=(x+4)(x﹣1)=x2+x﹣2,
则b=,c=﹣2;
(2)点E的横坐标为2,而点E在抛物线上,则点E(2,3),
将A、E的坐标代入y=mx+n得:,解得:,
故直线AE的表达式为:y=x+2,
点P(t,t2+t﹣2),则点F(t,t+2),
d=PF=t+2﹣(t2+t﹣2)=﹣t2﹣t+4(﹣4<t<2);
(3)点P(t,t2+t﹣2),分别过点E、K作PF的垂线交于点R、H,
PF把△PKE分成面积比为11:12的两个三角形,当ER:KH=12:11时,
即:(2﹣t):(t﹣xK)=12:11,
解得:xK=,
则yK=,点K在直线AE上,则点K(,),
∵PK⊥AE,则直线PK的表达式可设为:y=﹣2x+s,
将点K的坐标代入上式并解得:
直线PK的表达式为:y=﹣2x+,
将点P的坐标代入上式并化简得:12t2﹣31t+14=0,
解得:t=或2(舍去2);
PF把△PKE分成面积比为11:12的两个三角形,当ER:KH=11:12时,
同理可得:t=;
综上,t=或
同课章节目录
