2021年中考数学复习《探索二次函数综合型压轴题解题技巧》分类训练二:与角的度量有关的压轴题(附答案)
文档属性
| 名称 | 2021年中考数学复习《探索二次函数综合型压轴题解题技巧》分类训练二:与角的度量有关的压轴题(附答案) |  | |
| 格式 | doc | ||
| 文件大小 | 860.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-20 09:18:15 | ||
图片预览


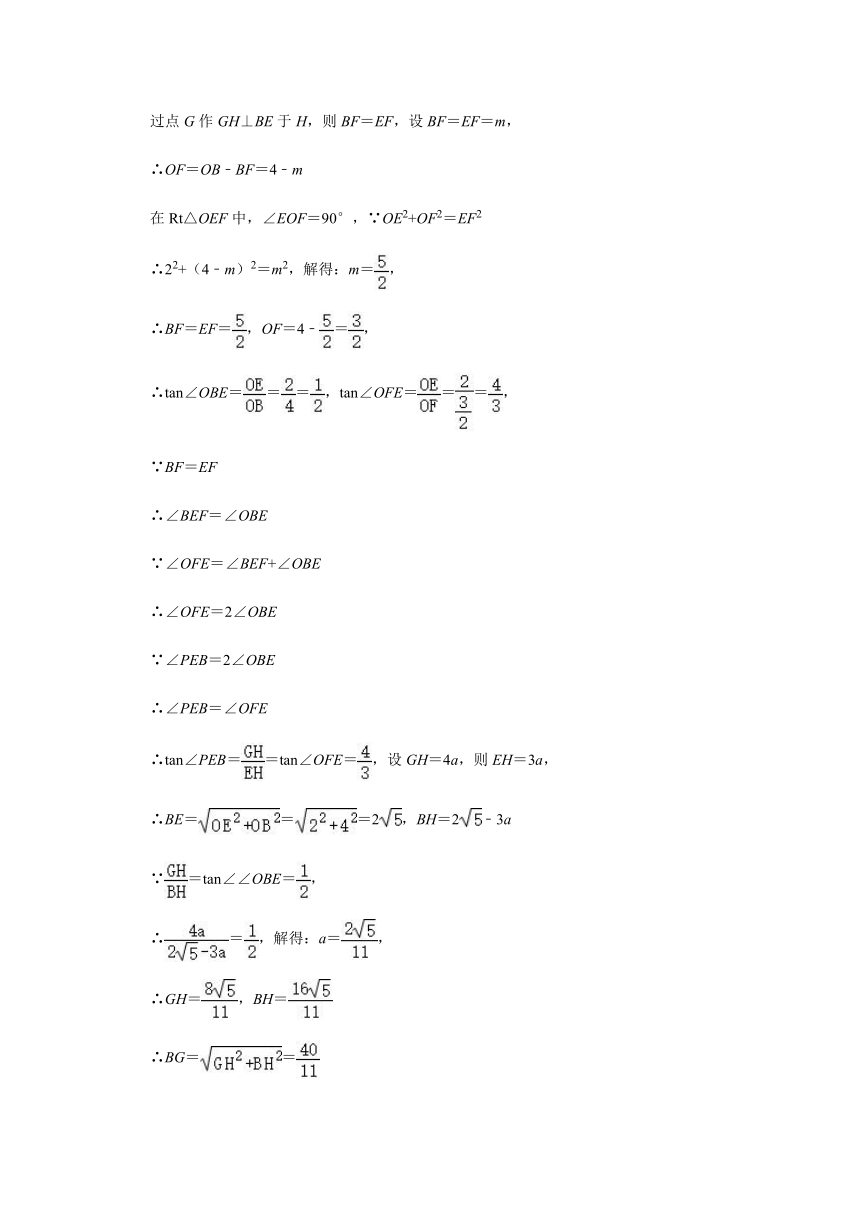


文档简介
2021中考数学复习《探索二次函数综合型压轴题解题技巧》分类训练二:
与角的度量关系相关的压轴题(附答案)
方法提炼:
1.将角的度量关系转化为边的数量,利用边的数量关系求解问题的答案。
2.利用角的度量关系,寻找问题中的特殊角,结合三角函数求解。
3.利用角的度量关系,构建图形的全等、相似,利用图形的全等、相似的性质求解
典例引领:
例:如图,抛物线y=ax2+3x+c(a<0)与x轴交于点A和点B(点A在原点的左侧,点B在原点的右侧),与y轴交于点C,OB=OC=4.
(1)求该抛物线的函数解析式.
(2)如图1,连接BC,点D是直线BC上方抛物线上的点,连接OD,CD.OD交BC于点F,当S△COF:S△CDF=4:3时,求点D的坐标.
(3)如图2,点E的坐标为(0,﹣2),点P是抛物线上的点,连接EB,PB,PE形成的△PBE中,是否存在点P,使∠PBE或∠PEB等于2∠OBE?若存在,请直接写出符合条件的点P的坐标;若不存在,请说明理由.
14.解:(1)∵OB=OC=4,
∴B(4,0),C(0,4),
把B(4,0),C(0,4)代入y=ax2+3x+c,得,解得
∴抛物线的函数解析式为y=﹣x2+3x+4;
(2)如图1,设直线BC解析式为y=kx+b,则,解得
∴直线BC解析式为y=﹣x+4,
令点D、F的横坐标分别为xD,xF,
∵S△COF:S△CDF=4:3,
∴S△COF=S△COD,即OC?xF=×OC?xD,
∴xD=xF,
设点D横坐标为7t,点F横坐标为4t,∵点F在直线BC上,
∴F(4t,4﹣4t),
设直线OF解析式为y=k′x,则4﹣4t=4tk′,
∴k′==,
∴直线OF解析式为y=x,
∵点D在直线OF上,
∴D(7t,7﹣7t),
将D(7t,7﹣7t)代入y=﹣x2+3x+4中,得7﹣7t=﹣(7t)2+3×7t+4,解得:t1=,t2=,
∴D的坐标为(1,6)或(3,4);
(3)①当∠PEB=2∠OBE,且点P在x轴上方时,如图2,作BE的垂直平分线交OB于F,连接EF,
在∠BEO内部作射线EP交x轴于G,交抛物线于P,使∠PEB=∠EFO,
过点G作GH⊥BE于H,则BF=EF,设BF=EF=m,
∴OF=OB﹣BF=4﹣m
在Rt△OEF中,∠EOF=90°,∵OE2+OF2=EF2
∴22+(4﹣m)2=m2,解得:m=,
∴BF=EF=,OF=4﹣=,
∴tan∠OBE===,tan∠OFE===,
∵BF=EF
∴∠BEF=∠OBE
∵∠OFE=∠BEF+∠OBE
∴∠OFE=2∠OBE
∵∠PEB=2∠OBE
∴∠PEB=∠OFE
∴tan∠PEB==tan∠OFE=,设GH=4a,则EH=3a,
∴BE===2,BH=2﹣3a
∵=tan∠∠OBE=,
∴=,解得:a=,
∴GH=,BH=
∴BG==
∴OG=OB﹣BG=4﹣=
∴G(,0),
设直线EG解析式为y=k″x+b″,则,解得
∴直线EG解析式为y=x﹣2,
联立方程组,解得:(舍去),,
∴P(,),
②当∠PEB=2∠OBE,且点P在x轴下方时,如图3,过点E作EF⊥y轴,作点B关于直线EF的对称点G,连接BG交EF于F,
射线EG交抛物线于点P,
∵E(0,﹣2),
∴直线EF为:y=﹣2
∵B(4,0),
∴G(4,﹣4)
∴直线EG解析式为y=﹣x﹣2,
解方程组,得,(不符合题意,舍去),
∴P(,);
③当∠PBE=2∠OBE,且点P在x轴上方时,如图4,在y轴正半轴上截取OF=OE=2,作射线BF交抛物线于P,
在△BOE和△BOF中,
∴△BOE≌△BOF(SAS)
∴∠PBO=∠OBE
∴∠PBE=2∠OBE
易求得直线PF解析式为y=﹣x+2,
联立方程组,解得(不符合题意,舍去),,
∴P(﹣,);
④当∠PBE=2∠OBE,且点P在x轴下方时,如图5,过点E作EF⊥BE交直线BP于F,过F作FG⊥y轴于G,
由①知:tan∠PBE==,BE=2
∴EF=
∵∠EGF=∠BOE=∠BEF=90°
∴∠BEO+∠FEG=∠BEO+OBE=90°
∴∠FEG=∠OBE
∴△EFG∽△BEO
∴==,即==
∴FG=,EG=
∴OG=OE+EG=2+=
∴F(,﹣)
易求得直线BF解析式为y=x﹣22,
联立方程组,解得(舍去),∴
∴P(﹣,﹣);
综上所述,符合条件的点P的坐标为:(,)、(,)、(﹣,)、(﹣,﹣).
跟踪训练:
1.如图,抛物线y=ax2+bx过A(4,0),B(1,3)两点.
(1)求该抛物线的解析式;
(2)点P是抛物线上一点,且位于第一象限,当△ABP的面积为3时,求出点P的坐标;
(3)过B作BC⊥OA于C,连接OB,点G是抛物线上一点,当∠BAG+∠OBC=∠BAO时,请直接写出此时点G的坐标.
2.如图,抛物线y=ax2+bx+与x轴交于点A(﹣5,0),B(1,0),顶点为D,与y轴交于点C.
(1)求抛物线的表达式及D点坐标;
(2)在直线AC上方的抛物线上是否存在点E,使得∠ECA=2∠CAB,如果存在这样的点E,求出△ACE面积,如果不存在,请说明理由.
3.如图1,抛物线y=﹣+bx+c经过原点(0,0),A(12,0)两点.
(1)求b的值;
(2)如图2,点P是第一象限内抛物线y=﹣+bx+c上一点,连接PO,若tan∠POA=,求点P的坐标;
(3)如图3,在(2)的条件下,过点P的直线y=﹣x+m与x轴交于点F,作CF=OF,连接OC交抛物线于点Q,点B在线段OF上,连接CP、CB、PB,PB交CF于点E,若∠PBA=2∠PCB,∠BEF=2∠BCF,求点Q的坐标.
4.如图,抛物线y=﹣+bx+c交x轴于点A、B(A在B左侧),交y轴于点C,直线y=﹣x+6经过点B、C.
(1)求抛物线解析式;
(2)点P为第一象限抛物线上一点,连接PA交BC于点D,设点P的横坐标为t,的值为d,求d与t的函数关系式(不要求写出自变量t的取值范围);
(3)在(2)的条件下,点E为线段OB上一点,连接CE,过点O作CE的垂线交BC于点G,连接PG并延长交OB于点F,若∠OGC=∠BGF,F为BE中点,求t的值.
5.抛物线y=ax2+c经过点(0,﹣1),交x轴于A(﹣1,0),B两点,点P是第一象限内抛物线上一动点.
(1)直接写出抛物线的解析式;
(2)如图1已知直线l的解析式为y=x﹣2,过点P作直线l的垂线,垂足为H,当PH=时,求点P的坐标;
(3)如图2,当∠APB=45°时,求点P的坐标.
6.已知抛物线y=x2﹣mx﹣m﹣1与x轴交于A、B两点,点A在点B的左边,与y轴交于点C(0,﹣3).
(1)求点A、B的坐标;
(2)点D是抛物线上一点,且∠ACO+∠BCD=45°,求点D的坐标;
(3)将抛物线向上平移m个单位,交线段BC于点M,N,若∠MON=45°,求m的值.
7.如图,在平面直角坐标系xOy中,已知点A(﹣1,0),D(﹣3,0),C(﹣4,3),四边形ABCD是平行四边形.现将?ABCD沿x轴方向平移n个单位,得到?A1B1C1D1,抛物线M经过点A1,C1,D1.
(1)若抛物线M的对称轴为直线x=4,求抛物线M的解析式;
(2)抛物线M的顶点为E,若以A,E,C1为顶点的三角形的面积等于?ABCD的面积的一半,求n的值;
(3)在(2)的条件下,在y轴上是否存在点P,使得∠C1PA=∠C1EA?若存在,请直接写出点P的坐标;若不存在,请说明理由.
8.如图,在平面直角坐标系中抛物线y=ax2+bx+c交x轴于点A、B,交y轴于点C,A、B两点横坐标为﹣1和3,C点纵坐标为﹣4.
(1)求抛物线的解析式;
(2)动点D在第四象限且在抛物线上,当△BCD面积最大时,求D点坐标,并求△BCD面积的最大值;
(3)抛物线的对称轴上是否存在一点Q,使得∠QBC=45°,如果存在,求出点Q的坐标,不存在说明理由.
9.抛物线y=﹣x2+bx+c与x轴相交于A、B两点(点A在点B的左侧),与y轴交于点C.直线y=﹣2x+6经过B、C两点,连接AC.
(1)求抛物线的解析式:
(2)点P是第一象限抛物线上一点,P点横坐标为t,连接PC、PB,设△PBC的面积为S,求S与t之间的函数关系式(直接写出自变量t的取值范围):
(3)在(2)问的条件下,当S=3且t<2时,连接PB,在抛物线上是否存在一点Q,使∠PBQ=∠ACB?若存在求出Q点坐标,若不存在,说明理由.
10.如图,在平面直角坐标系中,抛物线与x轴交于A、B两点,与y轴交于C点,B点与C点是直线y=x﹣3与x轴、y轴的交点.D为线段AB上一点.
(1)求抛物线的解析式及A点坐标.
(2)若点D在线段OB上,过D点作x轴的垂线与抛物线交于点E,求出点E到直线BC的距离的最大值.
(3)D为线段AB上一点,连接CD,作点B关于CD的对称点B′,连接AB′、B′D
①当点B′落坐标轴上时,求点D的坐标.
②在点D的运动过程中,△AB′D的内角能否等于45°,若能,求此时点B′的坐标;若不能,请说明理由.
11.如图,在平面直角坐标系中,抛物线y=ax2+x+c交x轴于点A、点B,交y轴于点C.直线y=﹣x+2经过于点C、点B,
(1)求抛物线的解析式;
(2)点D为第一象限抛物线上一动点,过点D作y轴的平行线交线段BC于点E,交x轴于点Q,当DE=5EQ时,求点D的坐标;
(3)在(2)的条件下,点M为第二象限抛物线上一动点,连接DM,DM交线段OC于点H,点F在线段OB上,连接HF、DF、DC、DB,当HF=,∠CDB=2∠MDF时,求点M的坐标.
12.已知抛物线y=ax2+bx﹣3与x轴交于点A(﹣1,0)、B两点,与y轴交于点C,且过点P(5,12).
(1)求抛物线的解析式.
(2)如图,点Q为线段CP上一动点,过点Q作QF⊥x轴于点F,交抛物线于点D,连接CD,PD,若S△QDC:S△QDP=2:3,求直线PD的解析式.
(3)过点B的直线交抛物线于M,是否存在点M使∠ABM=∠PCO,若存在,求出点M的坐标.若不存在,说明理由.
13.如图1,抛物线C1:y=x2+(m﹣2)x﹣2m(m>0)与x轴交于点A、B(A在B的左侧),与y轴交于点C,连接AC、BC,S△ABC=3.
(1)求m的值;
(2)如图2,将射线BC绕点B顺时针方向旋转交抛物线C1第二象限的图象于点D,连接DC.当x轴恰好三等分△DBC的面积时,求此时点D的横坐标;
(3)将抛物线C1向右平移,使新抛物线C2经过原点,如图3,C2的对称轴l交抛物线C2于E,交直线y=4于F,直线y=4交C2于点G、H(G在H的左侧),点M、N分别从点G、H同时出发,以1个单位长度/秒向点F运动.设点M运动时间为t(秒),点M、N到达F时,运动停止,点W在l上,WF=,连MW、NE.当∠MWF=3∠FEN时,求t的值.
参考答案
1.解:(1)将点A、B的坐标代入抛物线表达式并解得:
a=﹣1,b=4,
故抛物线的表达式为:y=﹣x2+4x…①;
(2)过点P作直线m交x轴于点M,过点P作PH⊥AB于点H,过点A作AN⊥直线m,
在AB下方作直线n距离直线AB的长度为PH,
△ABP的面积S=AB×PH=×3×PH=3,解得:PH==AN,
直线AB的倾斜角为45°,故直线m、n所在直线的k值为:﹣1,
则AM=AH=2,故点M(6,0),
则直线m的表达式为:y=﹣x+6…②,
同理直线n的表达式为:y=﹣x+2…③,
联立②①并解得:x=2或3,
联立③①并解得:x=(舍去);
综上,点P的坐标为:(3,3)或(2,4)或(,);
(3)∵BC=AC=3,故∠BAO=45°=∠BAG+∠OBC,
①当点G在AB上方时,如图2(左侧图),
设抛物线对称轴交x轴于点M,连接BM,
OC=OM=1,故∠CBM=∠OBC,
则∠CAB=45°=∠CBM+∠MBA=∠OBC+∠ABM,而45°=∠BAG+∠OBC,
故∠ABM=∠GAB,则AG∥BM,
直线BM表达式中的k值为:3,
故直线AG的表达式为:y=﹣3x+b,将点A的坐标代入上式并解得:
直线AG的表达式为:y=﹣3x+12…④;
联立①④并解得:x=3或4(舍去4);
②当点G在AB下方时,如图2(右侧图),
∠BAG+∠OBC=∠BAO=45°,而∠BAG+∠GAC=45°,
∴∠OBC=∠GAC,而tan∠OBC===tan∠GAC,
则直线AG的表达式为:y=﹣x+b′,将点A坐标代入上式并解得:
直线AG的表达式为:y=﹣x2+…⑤,
联立⑤①并解得:x=或4(舍去4).
综上,点P的坐标为:(3,3)或(,).
2.解:(1)∵抛物线y=ax2+bx+与x轴交于点A(﹣5,0),B(1,0),
∴,
∴
∴抛物线的表达式为:y=﹣x2﹣2x+,
∴顶点D(﹣2,)
(2)如图,过点C作CM∥AB,过点E作EF⊥CM,
设点E(m,﹣m2﹣2m+)
∵y=﹣x2﹣2x+交y轴交于点C,
∴点C(0,),
∴OC=,
∵CM∥AB,
∴∠MCA=∠CAB,
∵∠ECA=2∠CAB=∠ECF+∠MCA,
∴∠ECF=∠CAB,且∠AOC=∠EFC=90°,
∴△CEF∽△ACO,
∴,
∴=
∴m=0(不合题意),m=﹣3,
∴点E(﹣3,4),
∴S△AEC=×(+4)×3+×4×2﹣×5×=.
3.解:(1)∵抛物线y=﹣+bx+c经过原点(0,0),A(12,0)两点.
∴c=0,0=﹣×144+12b+c
∴b=;
(2)如图2,过点P作PE⊥OA于点E,
∵c=0,b=,
∴抛物线解析式为:y=﹣+x
∵点P是第一象限内抛物线y=﹣+x上一点,
∴设点P(m,﹣m2+m),(m>0)
∵tan∠POA==,
∴=,
∴m=8,
∴点P(8,4);
(3)连接OP,
∵直线y=﹣x+m过点P(8,4),
∴m=,
∴直线解析式为y=﹣x+,
当y=0,x=,
∴点F(,0),
∵∠BEF=∠BCF+∠PBC,且∠BEF=2∠BCF,
∴∠PBC=∠BCF,
∵∠PBA=2∠PCB,∠BEF=2∠BCF,
∴∠EFB=180°﹣2∠PCB﹣2∠PBC,
∵OF=CF,
∴∠COF=∠PCB+∠PBC=∠OCF,
∵∠CPB=180°﹣∠BCP﹣∠PBC,
∴∠CPB+∠COF=180°,
∴点O,点B,点P,点C四点共圆,
∴∠PBA=∠OCP,∠OCB=∠OPB,∠BCP=∠BOP,
∵∠PBA=2∠PCB,∠PBA=∠OCP=∠OCB+∠BCP,
∴∠OCB=∠BCP,
∴∠BPO=∠POB,
∴OB=PB,
设点B(a,0)
∴OB=BP=a,
∴a=
∴a=7
∴点B(7,0)
设过点O,点B,点P,点C四点的圆的圆心M(,y),
∵MO=MP,
∴()2+y2=(8﹣)2+(4﹣y)2,
∴y=,
∴M(,),
设点C(a,n)
∵MO=MC,OF=CF,
∴(a﹣)2+(b﹣)2=()2+()2 ①,
(a﹣)2+b2=()2 ②,
∴由①②组成方程组可求b=a,
设直线OC解析式为:y=kx,且过点C(a,b)
∴b=ka,
∴k=
∴直线OC解析式为:y=x,
∴x=﹣+x
∴x1=0(不合题意舍去),x2=4,
∴点Q(4,4)
4.解:(1)直线y=﹣x+6经过点B、C,则点B、C的坐标分别为:(6,0)、(0,6),则c=6,
将点A的坐标代入抛物线表达式并解得:b=2,
故抛物线的表达式为:y=﹣x2+2x+6…①;
(2)点P(t,﹣t2+2t+6),
将点P、A的坐标代入一次函数表达式:y=kx+b并解得:
直线AP的表达式为:y=﹣(t﹣6)x+(6﹣t),
将上式与直线BC的表达式联立并解得:x=,
故点D(,+6),
则=,则d==﹣1=﹣t2+t(0<t<6);
(3)设OE=a,则点E(a,0),设OG交CE于点H,
∵∠ECO+∠COH=90°,∠COH+∠HOE=90°,∴∠HOE=∠OCH,
tan∠OCH===tan∠HOE,则直线OH的表达式为:y=x…②,
联立①②并解得:x=,故点G(,),
则BG==,则CG=BC﹣BG=,
∵OB=OC=6,故∠OCB=∠OBC=45°,而∠OGC=∠BGF,
则△CGO∽△BGF,即:,即:,
解得:BF=a,F为BE中点,则OE=EF=FB,
故a=2,故点F(4,0),点G(,);
将点F、G的坐标代入一次函数表达式并解得:
直线FG的表达式为:y=3x﹣12…③,
联立①③并解得:x=﹣1(舍去负值),
故t=﹣1+.
5.解:(1)∵抛物线y=ax2+c经过点(0,﹣1),A(﹣1,0),
∴,
∴,
∴抛物线的解析式的解析式为y=x2﹣1;
(2)过点P作y轴的平行线交直线l于点M,
∵直线l的解析式为y=x﹣2,
∴直线与y轴的夹角为45°,
∴∠PMH=45°,
∵PH⊥MH,PH=,
∴PM=7,
设P(a,a2﹣1),则M(a,a﹣2),
∴PM=a2﹣1﹣a+2=7,
∴a1=3,a2=﹣2(舍去),
∴P(3,8);
(3)如图2,在y轴上取点D(0,1),则△ABD为等腰直角三角形,
∵AO=BO=1,∠ADB=90°,
∴=,
以点D为圆心、AD长为半径画圆,则点P在优弧AB上时总有∠APB=45°,
连结PD,设P点坐标为(m,m2﹣1),
∴PD==,
∴m2+(m2﹣2)2=2,
解得:,(舍去),m3=1(舍去),m4=﹣1(舍去),
∴P(,1).
6.解:(1)﹣m﹣1=﹣3,解得:m=2,
故抛物线的表达式为:y=x2﹣2x﹣3…①,
令y=0,解得:x=3或﹣1,
故点A、B的坐标分别为:(﹣1,0)、(3,0);
(2)①当点D在BC下方时,
∵∠ACO+∠BCD=45°,则AC⊥CD,
则直线CD的表达式为:y=x﹣3…②,
联立①②并解得:x=0或,
故点D(,﹣);
②当点D(D′)在BC上方时,
过点D作DE⊥BC交BC于点H,交CD′于点E,
直线BC的表达式为:y=x﹣3…③
则ED的表达式为:y=﹣x+…④,
联立③④并解得:x=,故点H(,﹣),点E的坐标为:(,﹣),
则直线CE的表达式为:y=3x﹣3…⑤,
联立①⑤并解得:x=0或5(舍去0),
故点D(D′)的坐标为:(5,12),
综上,点D的坐标为:(,﹣)或(5,12);
(3)如图2,抛物线平移后的图象为虚线部分,
则抛物线的表达式为:y=x2﹣2x﹣3+m(m>0),
设点M、N的坐标分别为:(x1,y1)、(x2、y2),
则x1+x2=3,x1x2=m,x2=,
∵∠MON=45°=∠OCM,∠ONM=∠ONM,
∴△NOM∽△NCO,
∴NO2=MN?CN,
而NO2=(x22+y22),MN=(x2﹣x1),CN=x22,
即(x22+y22)=2x2(x2﹣x1),
即2x1x2=x22﹣y22,而y2=x2﹣3,
故=+m,
解得:m=(﹣1+)(不合题意的值已舍去).
7.解:(1)四边形ABCD是平行四边形,则点B的坐标为:(﹣2,3),
即点B在AD的中垂线上,
过点A、D的二次函数表达式为:y=a(x+1)(x+3)=a(x2+4x+3),
将点C的坐标代入上式并解得:a=1,
则过A、C、D的抛物线为:y=x2+4x+3=(x+2)2﹣1,
抛物线M的对称轴为直线x=4,相当于将上述抛物线向右平移了6个单位,
故抛物线M的表达式为:y=(x﹣4)2﹣1;
(2)将?ABCD沿x轴方向平移n个单位,则点C1、E的坐标分别为:(n﹣4,3)、(n﹣2,﹣1),点A(﹣1,0),
连接C1E交x轴于点M,
将点C1、E的坐标代入一次函数表达式:y=kx+b并解得:
直线C1、E的表达式为:y=﹣2x+(2n﹣5),
则点M的坐标为:(,0),
S△AEC1=×AM×(yC1﹣yE)=(+1)×4=S?ABCD=×2×3=3,
解得:n=3;
(3)存在,理由:
由(2)知点C(﹣1,3),点A(﹣1,0),则AC⊥x轴,
故点A、C1、E作圆Q,则点Q在AC1的中垂线上,设点Q(m,),
则此时,∠C1PA=∠C1EA,
由QC1=QE得:(m+1)2+(3﹣)2=(m﹣1)2+(1+)2,解得:m=1,
则点Q(1,),设点P(0,t),
由QP=QE得:1+(﹣t)2=()2,解得:t=,
故点P的坐标为:(0,).
8.解:(1)抛物线的表达式为:y=a(x+1)(x﹣3)=a(x2﹣2x﹣3),
故﹣3a=﹣4,解得:a=,
故抛物线的表达式为:y=x2﹣x﹣4;
(2)过点D作y轴的平行线交BC于点N,
由B、C的坐标可得直线BC的表达式为:y=x﹣4,
设点D(x,x2﹣x﹣4),点N(x,x﹣4),
S△BCD=×OB×ND=3×(x﹣4﹣x2+x+4)=﹣2x2+6x,
∵﹣2<0,故S有最大值,
此时,x=,点D(,﹣5);
(3)存在,理由:
直线BC的表达式为:y=x﹣4,抛物线的对称轴为:x=1,故点H(1,﹣),
过点Q作QM⊥BC于点M,tan∠OCB==tanα,∠QBC=45°,
设QM=3x,则HM=4x,MB=3x,
BH=HM+MB=7x==,解得:x=,
QH=5x=,
则yQ=yH+=﹣,
故点Q(1,).
9.解:(1)直线y=﹣2x+6经过B、C两点,则点B、C的坐标为:(3,0),(0,6),
将点B、C的坐标代入抛物线表达式并解得:b=1,c=6,
故抛物线的表达式为:y=﹣x2+x+6…①;
(2)过点P作y轴的平行线交BC于点H,设点P(t,﹣t2+t+6),则点H(t,﹣2t+6),
S=×PH×OB=(﹣t2+t+6+2t﹣6)=﹣t2+t(0<t<3);
(3)S=3,即:﹣t2+t=3,解得:t=1或2(舍去2),故点P(1,6),而点B(0,3),
则直线PB的表达式为:y=﹣x+9,则点M(0,9),tan∠BMO=,
过点A作AL⊥BC于点L,
S△ABC=OC×AB=×BC×AL,即3×5=×AL×3,解得:AL=,
sin∠ACB==,则∠ACB=45°=∠MBQ,
设BQ交y轴于点H,过点H作HN⊥MB于点N,
tan∠BMO=,∠MBQ=45°,
设:HN=x,则BN=x,MN=3x,
MB=4x=,解得:x=,
HB=x=,则OH2=BH2﹣OB2=,
则点H(0,),
则BH的函数表达式为:y=﹣x+…②,
联立①②并解得:x=﹣(不合题意值已舍去),
则点Q(﹣,).
10.解:(1)∵B点与C点是直线y=x﹣3与x轴、y轴的交点.
∴B(3,0),C(0,﹣3),
∴,
解得:,
∴抛物线的解析式为,
令y=0,,
解得x1=﹣2,x2=3,
∴A(﹣2,0),
(2)设E点到直线BC的距离为d,E点横坐标为m,F(m,m﹣3),
∵B(3,0),C(0,﹣3),
∴∠OBC=45°,
如图1,过点E作EH⊥BC于点H,
则△EFH为等腰直角三角形,
∴EH=,
EF=yF﹣yE=m﹣3﹣(,
=(0≤m≤3),
=,
当时,EF的最大值为,
∴d=EF==.
即E到BC的最大距离为.
(3)①点B′在以C为圆心,CB为半径的圆C上;
(Ⅰ)当B′点落在x轴上时,D1(0,0);
(Ⅱ)当B′点落在y轴上时,如图2,CB′=CB=3,
∵∠OB′D=45°
∴OD=OB'=3﹣3,
∴;
②分别画出图形进行讨论求解:
(Ⅰ)∠B′DA=45°时,如图2,OB′=3﹣3,B′(0,3﹣3)
(Ⅱ)如图3,连接CB′,∠B′DA=∠CBD=45°,
∴DB′∥BC,可得四边形DB′CB是菱形,
B′(﹣3,﹣3).
(Ⅲ)∠B′AD=45°,如图4,连接CB′,过点B′分别作坐标轴的垂线,垂足为E、F,
设线段FB'的长为m,B′E=AE=2﹣m,可得CF=5﹣m,
在直角三角形CFB'中,m2+(5﹣m)2=(3)2,
解得m=,
故B′(),
(Ⅳ)如图5,∠AB′D=45°,连接CB',过点B′作y轴的垂线,垂足为点F,
由轴对称性质可得,∠CB′D=∠CBD=45°,所以当∠AB′D=45°时,点A在线段CB′上,
∴,
设线段FB′的长为2m,FC=3m,(2m)2+(3m)2=(3,
解得:m=,B′(﹣,
综合以上可得B′坐标为(0,)或或()或(﹣).
11.解:(1)针对于直线y=﹣x+2,令x=0,则y=2,
∴C(0,2),
令y=0,则0=﹣x+2,
∴x=4,
∴B(4,0),
将点B,C坐标代入抛物线y=ax2+x+c中,得
∴,
∴抛物线的解析式为y=﹣x2+x+2;
(2)如图1,由(1)知,抛物线的解析式为y=﹣x2+x+2,
设点D坐标为(m,﹣m2+m+2),
∵DE⊥x轴交BC于E,直线BC的解析式为y=﹣x+2,
∴D(m,﹣m+2),
∴DE=﹣m2+m+2﹣(﹣m+2)=﹣m2+m,DQ=﹣m+2,
∵DE=5EQ,
∴﹣m2+m=5(﹣m+2),
∴m=3或m=4(点B的横坐标,舍去),
∴D(3,3);
(3)如图2,
由(2)知,D(3,3),
由(1)知,B(4,0),C(0,2),
∴DB=,DC=,BC=2,
∴DC=DB,DB2+DC2=BC2,
∴△BDC是等腰直角三角形,
∴∠BDC=90°,
∵BDC=2∠FDM=90°,
∴∠FDM=45°,
过点D作DP⊥y轴于P,则DQ=DP,OP=3,
∴CP=1=BQ,
∴△DPC≌△DQB(SAS),
在CP的延长线取一点G,使PG=QF=n,
∴OF=3﹣n,OG=3+n,
∴△DPG≌△DQF(SAS),
∴DG=DF,∠PDG=∠QDF,
∴∠FDG=∠PDG+∠PDF=∠QDF+∠PDG=∠PDQ=90°
∴∠GDM=90°﹣∠FDM=45°=∠GDM,
∵DH=DH,
∴△GDH≌△FDH(SAS),
∴GH=FH=,
∴OH=OG﹣GH=3+n﹣=n+,
在Rt△HOF中,根据勾股定理得,(n+)2+(3﹣n)2=,
∴n=1或n=(此时,OH=n+=2,所以点H与点C重合,舍去),
∴H(0,),
∵C(3,3),
∴直线CH的解析式为y=x+①,
∵抛物线的解析式为y=﹣x2+x+2②,
联立①②解得,或(由于点M在第二象限,所以舍去),
∴M(﹣,).
12.解:(1)∵抛物线y=ax2+bx﹣3过点A(﹣1,0)、P(5,12)两点,
∴,
解得:,
∴抛物线的解析式为y=x2﹣2x﹣3;
(2)如图1,过点P作PN⊥y轴,QM⊥y轴,
∵S△QDC:S△QDP=2:3,
∴,
∴,
∵PN⊥y轴,QM⊥y轴,
∴QM∥PN,
∴△CQM∽△CPN,
∴,
∵PN=5,
∴QM=2,
∵QF⊥x轴于点F,交抛物线于点D,
∴D点的横坐标为2,
把x=2代入y=x2﹣2x﹣3=4﹣4﹣3=﹣3,
∴D(2,﹣3),
设直线PD的解析式为y=kx+b,
∴,
解得:,
∴直线PD的解析式为y=5x﹣13;
(3)如图2,过点P作PN⊥y轴,
∵P(5,12),C(0,﹣3),
∴CN=OC+ON=12+3=15,PN=5,
∴,
∵∠ABM=∠PCO,
∴,
如图2,若点M在x轴上方,
∵OB=3,
∴在y轴上取E(0,1),tan∠OBE=,
设直线BE的解析式为y=mx+n,
∴,
解得:m=﹣,
∴直线BE的解析式为y=﹣,
∴,
解得:x1=3,,
∴M(﹣),
如图3,当点M在x轴下方,同理取点D(0,﹣1),
求得直线BD的解析式为y=x﹣1,
∴,
解得:,
∴M(﹣,﹣),
综合以上可得M点的坐标为(﹣或(﹣).
13.解:(1)在y=x2+(m﹣2)x﹣2m(m>0)中,令x=0,得y=﹣2m,
∴C(0,﹣2m),
令y=0,得x2+(m﹣2)x﹣2m=0,解得:x1=2,x2=﹣m,
∴A(﹣m,0),B(2,0),
∴AB=2﹣(﹣m)=m+2,OC=2m
∵S△ABC=3
∴(m+2)?2m=3,解得:m1=1,m2=﹣3(不符合题意)
∴m=1;
∴抛物线C1:y=x2﹣x﹣2
(2)如图2,设D(t,t2﹣t﹣2),CD交x轴于K,作DT⊥x轴于T,
由(1)得:B(2,0),C(0,﹣2)
∵当x轴恰好三等分△DBC的面积时,有S△BDK=S△BCD或S△BDK=S△BCD
∴=或=,
①当=时,=
∴DT=OC
∴t2﹣t﹣2=×2,解得:t1=,t2=,
∵点D在第二象限,
∴t<0
∴t=,
②当=时,=2
∴DT=2OC
∴t2﹣t﹣2=2×2,解得:t1=3,t2=﹣2,
∵t<0
∴t=﹣2
综上所述,当x轴恰好三等分△DBC的面积时,点D的横坐标为或﹣2;
(3)如图3,取WE中点T,过点T作TR⊥EF交EN于点R,连接WR,WN,
由题意知:抛物线C1:y=x2﹣x﹣2=﹣,将抛物线C1向右平移,使新抛物线C2经过原点,
∴新抛物线C2解析式为y=(x﹣)2﹣=x2﹣3x,对称轴为:直线x=,顶点E(,﹣),
∴F(,4),EF=
在y=x2﹣3x中,令y=4,则4=x2﹣3x,解得:x1=﹣1,x2=4
∴G(﹣1,4),H(4,4)
∴GH=5
∵GM=NH=t,WF=,
∴MF=NF=﹣t,WE=﹣=5,WT=TE=WE=,
∵∠EFM=∠EFN=90°,WF=NF
∴△MWF≌△NWF(SAS)
∴∠MWF=∠NWF
∵∠MWF=3∠FEN
∴∠NWF=3∠FEN
∵∠NWF=∠FEN+∠ENW
∴∠ENW=2∠FEN
∵WT=ET,TR⊥EF
∴RW=RE
∴∠FEN=∠EWR
∴∠NRW=2∠FEN
∴∠ENW=∠NRW
∴RW=WN
∴RE=WN
由勾股定理得:EN2=EF2+NF2=+,WN2=WF2+NF2=+,
∵△ERT∽△ENF
∴=,即ER=EN
∴ER2=EN2=[+],
∴[+]=+,
解得:t1=(不符合题意,舍去),t2=,
故t=(秒).
与角的度量关系相关的压轴题(附答案)
方法提炼:
1.将角的度量关系转化为边的数量,利用边的数量关系求解问题的答案。
2.利用角的度量关系,寻找问题中的特殊角,结合三角函数求解。
3.利用角的度量关系,构建图形的全等、相似,利用图形的全等、相似的性质求解
典例引领:
例:如图,抛物线y=ax2+3x+c(a<0)与x轴交于点A和点B(点A在原点的左侧,点B在原点的右侧),与y轴交于点C,OB=OC=4.
(1)求该抛物线的函数解析式.
(2)如图1,连接BC,点D是直线BC上方抛物线上的点,连接OD,CD.OD交BC于点F,当S△COF:S△CDF=4:3时,求点D的坐标.
(3)如图2,点E的坐标为(0,﹣2),点P是抛物线上的点,连接EB,PB,PE形成的△PBE中,是否存在点P,使∠PBE或∠PEB等于2∠OBE?若存在,请直接写出符合条件的点P的坐标;若不存在,请说明理由.
14.解:(1)∵OB=OC=4,
∴B(4,0),C(0,4),
把B(4,0),C(0,4)代入y=ax2+3x+c,得,解得
∴抛物线的函数解析式为y=﹣x2+3x+4;
(2)如图1,设直线BC解析式为y=kx+b,则,解得
∴直线BC解析式为y=﹣x+4,
令点D、F的横坐标分别为xD,xF,
∵S△COF:S△CDF=4:3,
∴S△COF=S△COD,即OC?xF=×OC?xD,
∴xD=xF,
设点D横坐标为7t,点F横坐标为4t,∵点F在直线BC上,
∴F(4t,4﹣4t),
设直线OF解析式为y=k′x,则4﹣4t=4tk′,
∴k′==,
∴直线OF解析式为y=x,
∵点D在直线OF上,
∴D(7t,7﹣7t),
将D(7t,7﹣7t)代入y=﹣x2+3x+4中,得7﹣7t=﹣(7t)2+3×7t+4,解得:t1=,t2=,
∴D的坐标为(1,6)或(3,4);
(3)①当∠PEB=2∠OBE,且点P在x轴上方时,如图2,作BE的垂直平分线交OB于F,连接EF,
在∠BEO内部作射线EP交x轴于G,交抛物线于P,使∠PEB=∠EFO,
过点G作GH⊥BE于H,则BF=EF,设BF=EF=m,
∴OF=OB﹣BF=4﹣m
在Rt△OEF中,∠EOF=90°,∵OE2+OF2=EF2
∴22+(4﹣m)2=m2,解得:m=,
∴BF=EF=,OF=4﹣=,
∴tan∠OBE===,tan∠OFE===,
∵BF=EF
∴∠BEF=∠OBE
∵∠OFE=∠BEF+∠OBE
∴∠OFE=2∠OBE
∵∠PEB=2∠OBE
∴∠PEB=∠OFE
∴tan∠PEB==tan∠OFE=,设GH=4a,则EH=3a,
∴BE===2,BH=2﹣3a
∵=tan∠∠OBE=,
∴=,解得:a=,
∴GH=,BH=
∴BG==
∴OG=OB﹣BG=4﹣=
∴G(,0),
设直线EG解析式为y=k″x+b″,则,解得
∴直线EG解析式为y=x﹣2,
联立方程组,解得:(舍去),,
∴P(,),
②当∠PEB=2∠OBE,且点P在x轴下方时,如图3,过点E作EF⊥y轴,作点B关于直线EF的对称点G,连接BG交EF于F,
射线EG交抛物线于点P,
∵E(0,﹣2),
∴直线EF为:y=﹣2
∵B(4,0),
∴G(4,﹣4)
∴直线EG解析式为y=﹣x﹣2,
解方程组,得,(不符合题意,舍去),
∴P(,);
③当∠PBE=2∠OBE,且点P在x轴上方时,如图4,在y轴正半轴上截取OF=OE=2,作射线BF交抛物线于P,
在△BOE和△BOF中,
∴△BOE≌△BOF(SAS)
∴∠PBO=∠OBE
∴∠PBE=2∠OBE
易求得直线PF解析式为y=﹣x+2,
联立方程组,解得(不符合题意,舍去),,
∴P(﹣,);
④当∠PBE=2∠OBE,且点P在x轴下方时,如图5,过点E作EF⊥BE交直线BP于F,过F作FG⊥y轴于G,
由①知:tan∠PBE==,BE=2
∴EF=
∵∠EGF=∠BOE=∠BEF=90°
∴∠BEO+∠FEG=∠BEO+OBE=90°
∴∠FEG=∠OBE
∴△EFG∽△BEO
∴==,即==
∴FG=,EG=
∴OG=OE+EG=2+=
∴F(,﹣)
易求得直线BF解析式为y=x﹣22,
联立方程组,解得(舍去),∴
∴P(﹣,﹣);
综上所述,符合条件的点P的坐标为:(,)、(,)、(﹣,)、(﹣,﹣).
跟踪训练:
1.如图,抛物线y=ax2+bx过A(4,0),B(1,3)两点.
(1)求该抛物线的解析式;
(2)点P是抛物线上一点,且位于第一象限,当△ABP的面积为3时,求出点P的坐标;
(3)过B作BC⊥OA于C,连接OB,点G是抛物线上一点,当∠BAG+∠OBC=∠BAO时,请直接写出此时点G的坐标.
2.如图,抛物线y=ax2+bx+与x轴交于点A(﹣5,0),B(1,0),顶点为D,与y轴交于点C.
(1)求抛物线的表达式及D点坐标;
(2)在直线AC上方的抛物线上是否存在点E,使得∠ECA=2∠CAB,如果存在这样的点E,求出△ACE面积,如果不存在,请说明理由.
3.如图1,抛物线y=﹣+bx+c经过原点(0,0),A(12,0)两点.
(1)求b的值;
(2)如图2,点P是第一象限内抛物线y=﹣+bx+c上一点,连接PO,若tan∠POA=,求点P的坐标;
(3)如图3,在(2)的条件下,过点P的直线y=﹣x+m与x轴交于点F,作CF=OF,连接OC交抛物线于点Q,点B在线段OF上,连接CP、CB、PB,PB交CF于点E,若∠PBA=2∠PCB,∠BEF=2∠BCF,求点Q的坐标.
4.如图,抛物线y=﹣+bx+c交x轴于点A、B(A在B左侧),交y轴于点C,直线y=﹣x+6经过点B、C.
(1)求抛物线解析式;
(2)点P为第一象限抛物线上一点,连接PA交BC于点D,设点P的横坐标为t,的值为d,求d与t的函数关系式(不要求写出自变量t的取值范围);
(3)在(2)的条件下,点E为线段OB上一点,连接CE,过点O作CE的垂线交BC于点G,连接PG并延长交OB于点F,若∠OGC=∠BGF,F为BE中点,求t的值.
5.抛物线y=ax2+c经过点(0,﹣1),交x轴于A(﹣1,0),B两点,点P是第一象限内抛物线上一动点.
(1)直接写出抛物线的解析式;
(2)如图1已知直线l的解析式为y=x﹣2,过点P作直线l的垂线,垂足为H,当PH=时,求点P的坐标;
(3)如图2,当∠APB=45°时,求点P的坐标.
6.已知抛物线y=x2﹣mx﹣m﹣1与x轴交于A、B两点,点A在点B的左边,与y轴交于点C(0,﹣3).
(1)求点A、B的坐标;
(2)点D是抛物线上一点,且∠ACO+∠BCD=45°,求点D的坐标;
(3)将抛物线向上平移m个单位,交线段BC于点M,N,若∠MON=45°,求m的值.
7.如图,在平面直角坐标系xOy中,已知点A(﹣1,0),D(﹣3,0),C(﹣4,3),四边形ABCD是平行四边形.现将?ABCD沿x轴方向平移n个单位,得到?A1B1C1D1,抛物线M经过点A1,C1,D1.
(1)若抛物线M的对称轴为直线x=4,求抛物线M的解析式;
(2)抛物线M的顶点为E,若以A,E,C1为顶点的三角形的面积等于?ABCD的面积的一半,求n的值;
(3)在(2)的条件下,在y轴上是否存在点P,使得∠C1PA=∠C1EA?若存在,请直接写出点P的坐标;若不存在,请说明理由.
8.如图,在平面直角坐标系中抛物线y=ax2+bx+c交x轴于点A、B,交y轴于点C,A、B两点横坐标为﹣1和3,C点纵坐标为﹣4.
(1)求抛物线的解析式;
(2)动点D在第四象限且在抛物线上,当△BCD面积最大时,求D点坐标,并求△BCD面积的最大值;
(3)抛物线的对称轴上是否存在一点Q,使得∠QBC=45°,如果存在,求出点Q的坐标,不存在说明理由.
9.抛物线y=﹣x2+bx+c与x轴相交于A、B两点(点A在点B的左侧),与y轴交于点C.直线y=﹣2x+6经过B、C两点,连接AC.
(1)求抛物线的解析式:
(2)点P是第一象限抛物线上一点,P点横坐标为t,连接PC、PB,设△PBC的面积为S,求S与t之间的函数关系式(直接写出自变量t的取值范围):
(3)在(2)问的条件下,当S=3且t<2时,连接PB,在抛物线上是否存在一点Q,使∠PBQ=∠ACB?若存在求出Q点坐标,若不存在,说明理由.
10.如图,在平面直角坐标系中,抛物线与x轴交于A、B两点,与y轴交于C点,B点与C点是直线y=x﹣3与x轴、y轴的交点.D为线段AB上一点.
(1)求抛物线的解析式及A点坐标.
(2)若点D在线段OB上,过D点作x轴的垂线与抛物线交于点E,求出点E到直线BC的距离的最大值.
(3)D为线段AB上一点,连接CD,作点B关于CD的对称点B′,连接AB′、B′D
①当点B′落坐标轴上时,求点D的坐标.
②在点D的运动过程中,△AB′D的内角能否等于45°,若能,求此时点B′的坐标;若不能,请说明理由.
11.如图,在平面直角坐标系中,抛物线y=ax2+x+c交x轴于点A、点B,交y轴于点C.直线y=﹣x+2经过于点C、点B,
(1)求抛物线的解析式;
(2)点D为第一象限抛物线上一动点,过点D作y轴的平行线交线段BC于点E,交x轴于点Q,当DE=5EQ时,求点D的坐标;
(3)在(2)的条件下,点M为第二象限抛物线上一动点,连接DM,DM交线段OC于点H,点F在线段OB上,连接HF、DF、DC、DB,当HF=,∠CDB=2∠MDF时,求点M的坐标.
12.已知抛物线y=ax2+bx﹣3与x轴交于点A(﹣1,0)、B两点,与y轴交于点C,且过点P(5,12).
(1)求抛物线的解析式.
(2)如图,点Q为线段CP上一动点,过点Q作QF⊥x轴于点F,交抛物线于点D,连接CD,PD,若S△QDC:S△QDP=2:3,求直线PD的解析式.
(3)过点B的直线交抛物线于M,是否存在点M使∠ABM=∠PCO,若存在,求出点M的坐标.若不存在,说明理由.
13.如图1,抛物线C1:y=x2+(m﹣2)x﹣2m(m>0)与x轴交于点A、B(A在B的左侧),与y轴交于点C,连接AC、BC,S△ABC=3.
(1)求m的值;
(2)如图2,将射线BC绕点B顺时针方向旋转交抛物线C1第二象限的图象于点D,连接DC.当x轴恰好三等分△DBC的面积时,求此时点D的横坐标;
(3)将抛物线C1向右平移,使新抛物线C2经过原点,如图3,C2的对称轴l交抛物线C2于E,交直线y=4于F,直线y=4交C2于点G、H(G在H的左侧),点M、N分别从点G、H同时出发,以1个单位长度/秒向点F运动.设点M运动时间为t(秒),点M、N到达F时,运动停止,点W在l上,WF=,连MW、NE.当∠MWF=3∠FEN时,求t的值.
参考答案
1.解:(1)将点A、B的坐标代入抛物线表达式并解得:
a=﹣1,b=4,
故抛物线的表达式为:y=﹣x2+4x…①;
(2)过点P作直线m交x轴于点M,过点P作PH⊥AB于点H,过点A作AN⊥直线m,
在AB下方作直线n距离直线AB的长度为PH,
△ABP的面积S=AB×PH=×3×PH=3,解得:PH==AN,
直线AB的倾斜角为45°,故直线m、n所在直线的k值为:﹣1,
则AM=AH=2,故点M(6,0),
则直线m的表达式为:y=﹣x+6…②,
同理直线n的表达式为:y=﹣x+2…③,
联立②①并解得:x=2或3,
联立③①并解得:x=(舍去);
综上,点P的坐标为:(3,3)或(2,4)或(,);
(3)∵BC=AC=3,故∠BAO=45°=∠BAG+∠OBC,
①当点G在AB上方时,如图2(左侧图),
设抛物线对称轴交x轴于点M,连接BM,
OC=OM=1,故∠CBM=∠OBC,
则∠CAB=45°=∠CBM+∠MBA=∠OBC+∠ABM,而45°=∠BAG+∠OBC,
故∠ABM=∠GAB,则AG∥BM,
直线BM表达式中的k值为:3,
故直线AG的表达式为:y=﹣3x+b,将点A的坐标代入上式并解得:
直线AG的表达式为:y=﹣3x+12…④;
联立①④并解得:x=3或4(舍去4);
②当点G在AB下方时,如图2(右侧图),
∠BAG+∠OBC=∠BAO=45°,而∠BAG+∠GAC=45°,
∴∠OBC=∠GAC,而tan∠OBC===tan∠GAC,
则直线AG的表达式为:y=﹣x+b′,将点A坐标代入上式并解得:
直线AG的表达式为:y=﹣x2+…⑤,
联立⑤①并解得:x=或4(舍去4).
综上,点P的坐标为:(3,3)或(,).
2.解:(1)∵抛物线y=ax2+bx+与x轴交于点A(﹣5,0),B(1,0),
∴,
∴
∴抛物线的表达式为:y=﹣x2﹣2x+,
∴顶点D(﹣2,)
(2)如图,过点C作CM∥AB,过点E作EF⊥CM,
设点E(m,﹣m2﹣2m+)
∵y=﹣x2﹣2x+交y轴交于点C,
∴点C(0,),
∴OC=,
∵CM∥AB,
∴∠MCA=∠CAB,
∵∠ECA=2∠CAB=∠ECF+∠MCA,
∴∠ECF=∠CAB,且∠AOC=∠EFC=90°,
∴△CEF∽△ACO,
∴,
∴=
∴m=0(不合题意),m=﹣3,
∴点E(﹣3,4),
∴S△AEC=×(+4)×3+×4×2﹣×5×=.
3.解:(1)∵抛物线y=﹣+bx+c经过原点(0,0),A(12,0)两点.
∴c=0,0=﹣×144+12b+c
∴b=;
(2)如图2,过点P作PE⊥OA于点E,
∵c=0,b=,
∴抛物线解析式为:y=﹣+x
∵点P是第一象限内抛物线y=﹣+x上一点,
∴设点P(m,﹣m2+m),(m>0)
∵tan∠POA==,
∴=,
∴m=8,
∴点P(8,4);
(3)连接OP,
∵直线y=﹣x+m过点P(8,4),
∴m=,
∴直线解析式为y=﹣x+,
当y=0,x=,
∴点F(,0),
∵∠BEF=∠BCF+∠PBC,且∠BEF=2∠BCF,
∴∠PBC=∠BCF,
∵∠PBA=2∠PCB,∠BEF=2∠BCF,
∴∠EFB=180°﹣2∠PCB﹣2∠PBC,
∵OF=CF,
∴∠COF=∠PCB+∠PBC=∠OCF,
∵∠CPB=180°﹣∠BCP﹣∠PBC,
∴∠CPB+∠COF=180°,
∴点O,点B,点P,点C四点共圆,
∴∠PBA=∠OCP,∠OCB=∠OPB,∠BCP=∠BOP,
∵∠PBA=2∠PCB,∠PBA=∠OCP=∠OCB+∠BCP,
∴∠OCB=∠BCP,
∴∠BPO=∠POB,
∴OB=PB,
设点B(a,0)
∴OB=BP=a,
∴a=
∴a=7
∴点B(7,0)
设过点O,点B,点P,点C四点的圆的圆心M(,y),
∵MO=MP,
∴()2+y2=(8﹣)2+(4﹣y)2,
∴y=,
∴M(,),
设点C(a,n)
∵MO=MC,OF=CF,
∴(a﹣)2+(b﹣)2=()2+()2 ①,
(a﹣)2+b2=()2 ②,
∴由①②组成方程组可求b=a,
设直线OC解析式为:y=kx,且过点C(a,b)
∴b=ka,
∴k=
∴直线OC解析式为:y=x,
∴x=﹣+x
∴x1=0(不合题意舍去),x2=4,
∴点Q(4,4)
4.解:(1)直线y=﹣x+6经过点B、C,则点B、C的坐标分别为:(6,0)、(0,6),则c=6,
将点A的坐标代入抛物线表达式并解得:b=2,
故抛物线的表达式为:y=﹣x2+2x+6…①;
(2)点P(t,﹣t2+2t+6),
将点P、A的坐标代入一次函数表达式:y=kx+b并解得:
直线AP的表达式为:y=﹣(t﹣6)x+(6﹣t),
将上式与直线BC的表达式联立并解得:x=,
故点D(,+6),
则=,则d==﹣1=﹣t2+t(0<t<6);
(3)设OE=a,则点E(a,0),设OG交CE于点H,
∵∠ECO+∠COH=90°,∠COH+∠HOE=90°,∴∠HOE=∠OCH,
tan∠OCH===tan∠HOE,则直线OH的表达式为:y=x…②,
联立①②并解得:x=,故点G(,),
则BG==,则CG=BC﹣BG=,
∵OB=OC=6,故∠OCB=∠OBC=45°,而∠OGC=∠BGF,
则△CGO∽△BGF,即:,即:,
解得:BF=a,F为BE中点,则OE=EF=FB,
故a=2,故点F(4,0),点G(,);
将点F、G的坐标代入一次函数表达式并解得:
直线FG的表达式为:y=3x﹣12…③,
联立①③并解得:x=﹣1(舍去负值),
故t=﹣1+.
5.解:(1)∵抛物线y=ax2+c经过点(0,﹣1),A(﹣1,0),
∴,
∴,
∴抛物线的解析式的解析式为y=x2﹣1;
(2)过点P作y轴的平行线交直线l于点M,
∵直线l的解析式为y=x﹣2,
∴直线与y轴的夹角为45°,
∴∠PMH=45°,
∵PH⊥MH,PH=,
∴PM=7,
设P(a,a2﹣1),则M(a,a﹣2),
∴PM=a2﹣1﹣a+2=7,
∴a1=3,a2=﹣2(舍去),
∴P(3,8);
(3)如图2,在y轴上取点D(0,1),则△ABD为等腰直角三角形,
∵AO=BO=1,∠ADB=90°,
∴=,
以点D为圆心、AD长为半径画圆,则点P在优弧AB上时总有∠APB=45°,
连结PD,设P点坐标为(m,m2﹣1),
∴PD==,
∴m2+(m2﹣2)2=2,
解得:,(舍去),m3=1(舍去),m4=﹣1(舍去),
∴P(,1).
6.解:(1)﹣m﹣1=﹣3,解得:m=2,
故抛物线的表达式为:y=x2﹣2x﹣3…①,
令y=0,解得:x=3或﹣1,
故点A、B的坐标分别为:(﹣1,0)、(3,0);
(2)①当点D在BC下方时,
∵∠ACO+∠BCD=45°,则AC⊥CD,
则直线CD的表达式为:y=x﹣3…②,
联立①②并解得:x=0或,
故点D(,﹣);
②当点D(D′)在BC上方时,
过点D作DE⊥BC交BC于点H,交CD′于点E,
直线BC的表达式为:y=x﹣3…③
则ED的表达式为:y=﹣x+…④,
联立③④并解得:x=,故点H(,﹣),点E的坐标为:(,﹣),
则直线CE的表达式为:y=3x﹣3…⑤,
联立①⑤并解得:x=0或5(舍去0),
故点D(D′)的坐标为:(5,12),
综上,点D的坐标为:(,﹣)或(5,12);
(3)如图2,抛物线平移后的图象为虚线部分,
则抛物线的表达式为:y=x2﹣2x﹣3+m(m>0),
设点M、N的坐标分别为:(x1,y1)、(x2、y2),
则x1+x2=3,x1x2=m,x2=,
∵∠MON=45°=∠OCM,∠ONM=∠ONM,
∴△NOM∽△NCO,
∴NO2=MN?CN,
而NO2=(x22+y22),MN=(x2﹣x1),CN=x22,
即(x22+y22)=2x2(x2﹣x1),
即2x1x2=x22﹣y22,而y2=x2﹣3,
故=+m,
解得:m=(﹣1+)(不合题意的值已舍去).
7.解:(1)四边形ABCD是平行四边形,则点B的坐标为:(﹣2,3),
即点B在AD的中垂线上,
过点A、D的二次函数表达式为:y=a(x+1)(x+3)=a(x2+4x+3),
将点C的坐标代入上式并解得:a=1,
则过A、C、D的抛物线为:y=x2+4x+3=(x+2)2﹣1,
抛物线M的对称轴为直线x=4,相当于将上述抛物线向右平移了6个单位,
故抛物线M的表达式为:y=(x﹣4)2﹣1;
(2)将?ABCD沿x轴方向平移n个单位,则点C1、E的坐标分别为:(n﹣4,3)、(n﹣2,﹣1),点A(﹣1,0),
连接C1E交x轴于点M,
将点C1、E的坐标代入一次函数表达式:y=kx+b并解得:
直线C1、E的表达式为:y=﹣2x+(2n﹣5),
则点M的坐标为:(,0),
S△AEC1=×AM×(yC1﹣yE)=(+1)×4=S?ABCD=×2×3=3,
解得:n=3;
(3)存在,理由:
由(2)知点C(﹣1,3),点A(﹣1,0),则AC⊥x轴,
故点A、C1、E作圆Q,则点Q在AC1的中垂线上,设点Q(m,),
则此时,∠C1PA=∠C1EA,
由QC1=QE得:(m+1)2+(3﹣)2=(m﹣1)2+(1+)2,解得:m=1,
则点Q(1,),设点P(0,t),
由QP=QE得:1+(﹣t)2=()2,解得:t=,
故点P的坐标为:(0,).
8.解:(1)抛物线的表达式为:y=a(x+1)(x﹣3)=a(x2﹣2x﹣3),
故﹣3a=﹣4,解得:a=,
故抛物线的表达式为:y=x2﹣x﹣4;
(2)过点D作y轴的平行线交BC于点N,
由B、C的坐标可得直线BC的表达式为:y=x﹣4,
设点D(x,x2﹣x﹣4),点N(x,x﹣4),
S△BCD=×OB×ND=3×(x﹣4﹣x2+x+4)=﹣2x2+6x,
∵﹣2<0,故S有最大值,
此时,x=,点D(,﹣5);
(3)存在,理由:
直线BC的表达式为:y=x﹣4,抛物线的对称轴为:x=1,故点H(1,﹣),
过点Q作QM⊥BC于点M,tan∠OCB==tanα,∠QBC=45°,
设QM=3x,则HM=4x,MB=3x,
BH=HM+MB=7x==,解得:x=,
QH=5x=,
则yQ=yH+=﹣,
故点Q(1,).
9.解:(1)直线y=﹣2x+6经过B、C两点,则点B、C的坐标为:(3,0),(0,6),
将点B、C的坐标代入抛物线表达式并解得:b=1,c=6,
故抛物线的表达式为:y=﹣x2+x+6…①;
(2)过点P作y轴的平行线交BC于点H,设点P(t,﹣t2+t+6),则点H(t,﹣2t+6),
S=×PH×OB=(﹣t2+t+6+2t﹣6)=﹣t2+t(0<t<3);
(3)S=3,即:﹣t2+t=3,解得:t=1或2(舍去2),故点P(1,6),而点B(0,3),
则直线PB的表达式为:y=﹣x+9,则点M(0,9),tan∠BMO=,
过点A作AL⊥BC于点L,
S△ABC=OC×AB=×BC×AL,即3×5=×AL×3,解得:AL=,
sin∠ACB==,则∠ACB=45°=∠MBQ,
设BQ交y轴于点H,过点H作HN⊥MB于点N,
tan∠BMO=,∠MBQ=45°,
设:HN=x,则BN=x,MN=3x,
MB=4x=,解得:x=,
HB=x=,则OH2=BH2﹣OB2=,
则点H(0,),
则BH的函数表达式为:y=﹣x+…②,
联立①②并解得:x=﹣(不合题意值已舍去),
则点Q(﹣,).
10.解:(1)∵B点与C点是直线y=x﹣3与x轴、y轴的交点.
∴B(3,0),C(0,﹣3),
∴,
解得:,
∴抛物线的解析式为,
令y=0,,
解得x1=﹣2,x2=3,
∴A(﹣2,0),
(2)设E点到直线BC的距离为d,E点横坐标为m,F(m,m﹣3),
∵B(3,0),C(0,﹣3),
∴∠OBC=45°,
如图1,过点E作EH⊥BC于点H,
则△EFH为等腰直角三角形,
∴EH=,
EF=yF﹣yE=m﹣3﹣(,
=(0≤m≤3),
=,
当时,EF的最大值为,
∴d=EF==.
即E到BC的最大距离为.
(3)①点B′在以C为圆心,CB为半径的圆C上;
(Ⅰ)当B′点落在x轴上时,D1(0,0);
(Ⅱ)当B′点落在y轴上时,如图2,CB′=CB=3,
∵∠OB′D=45°
∴OD=OB'=3﹣3,
∴;
②分别画出图形进行讨论求解:
(Ⅰ)∠B′DA=45°时,如图2,OB′=3﹣3,B′(0,3﹣3)
(Ⅱ)如图3,连接CB′,∠B′DA=∠CBD=45°,
∴DB′∥BC,可得四边形DB′CB是菱形,
B′(﹣3,﹣3).
(Ⅲ)∠B′AD=45°,如图4,连接CB′,过点B′分别作坐标轴的垂线,垂足为E、F,
设线段FB'的长为m,B′E=AE=2﹣m,可得CF=5﹣m,
在直角三角形CFB'中,m2+(5﹣m)2=(3)2,
解得m=,
故B′(),
(Ⅳ)如图5,∠AB′D=45°,连接CB',过点B′作y轴的垂线,垂足为点F,
由轴对称性质可得,∠CB′D=∠CBD=45°,所以当∠AB′D=45°时,点A在线段CB′上,
∴,
设线段FB′的长为2m,FC=3m,(2m)2+(3m)2=(3,
解得:m=,B′(﹣,
综合以上可得B′坐标为(0,)或或()或(﹣).
11.解:(1)针对于直线y=﹣x+2,令x=0,则y=2,
∴C(0,2),
令y=0,则0=﹣x+2,
∴x=4,
∴B(4,0),
将点B,C坐标代入抛物线y=ax2+x+c中,得
∴,
∴抛物线的解析式为y=﹣x2+x+2;
(2)如图1,由(1)知,抛物线的解析式为y=﹣x2+x+2,
设点D坐标为(m,﹣m2+m+2),
∵DE⊥x轴交BC于E,直线BC的解析式为y=﹣x+2,
∴D(m,﹣m+2),
∴DE=﹣m2+m+2﹣(﹣m+2)=﹣m2+m,DQ=﹣m+2,
∵DE=5EQ,
∴﹣m2+m=5(﹣m+2),
∴m=3或m=4(点B的横坐标,舍去),
∴D(3,3);
(3)如图2,
由(2)知,D(3,3),
由(1)知,B(4,0),C(0,2),
∴DB=,DC=,BC=2,
∴DC=DB,DB2+DC2=BC2,
∴△BDC是等腰直角三角形,
∴∠BDC=90°,
∵BDC=2∠FDM=90°,
∴∠FDM=45°,
过点D作DP⊥y轴于P,则DQ=DP,OP=3,
∴CP=1=BQ,
∴△DPC≌△DQB(SAS),
在CP的延长线取一点G,使PG=QF=n,
∴OF=3﹣n,OG=3+n,
∴△DPG≌△DQF(SAS),
∴DG=DF,∠PDG=∠QDF,
∴∠FDG=∠PDG+∠PDF=∠QDF+∠PDG=∠PDQ=90°
∴∠GDM=90°﹣∠FDM=45°=∠GDM,
∵DH=DH,
∴△GDH≌△FDH(SAS),
∴GH=FH=,
∴OH=OG﹣GH=3+n﹣=n+,
在Rt△HOF中,根据勾股定理得,(n+)2+(3﹣n)2=,
∴n=1或n=(此时,OH=n+=2,所以点H与点C重合,舍去),
∴H(0,),
∵C(3,3),
∴直线CH的解析式为y=x+①,
∵抛物线的解析式为y=﹣x2+x+2②,
联立①②解得,或(由于点M在第二象限,所以舍去),
∴M(﹣,).
12.解:(1)∵抛物线y=ax2+bx﹣3过点A(﹣1,0)、P(5,12)两点,
∴,
解得:,
∴抛物线的解析式为y=x2﹣2x﹣3;
(2)如图1,过点P作PN⊥y轴,QM⊥y轴,
∵S△QDC:S△QDP=2:3,
∴,
∴,
∵PN⊥y轴,QM⊥y轴,
∴QM∥PN,
∴△CQM∽△CPN,
∴,
∵PN=5,
∴QM=2,
∵QF⊥x轴于点F,交抛物线于点D,
∴D点的横坐标为2,
把x=2代入y=x2﹣2x﹣3=4﹣4﹣3=﹣3,
∴D(2,﹣3),
设直线PD的解析式为y=kx+b,
∴,
解得:,
∴直线PD的解析式为y=5x﹣13;
(3)如图2,过点P作PN⊥y轴,
∵P(5,12),C(0,﹣3),
∴CN=OC+ON=12+3=15,PN=5,
∴,
∵∠ABM=∠PCO,
∴,
如图2,若点M在x轴上方,
∵OB=3,
∴在y轴上取E(0,1),tan∠OBE=,
设直线BE的解析式为y=mx+n,
∴,
解得:m=﹣,
∴直线BE的解析式为y=﹣,
∴,
解得:x1=3,,
∴M(﹣),
如图3,当点M在x轴下方,同理取点D(0,﹣1),
求得直线BD的解析式为y=x﹣1,
∴,
解得:,
∴M(﹣,﹣),
综合以上可得M点的坐标为(﹣或(﹣).
13.解:(1)在y=x2+(m﹣2)x﹣2m(m>0)中,令x=0,得y=﹣2m,
∴C(0,﹣2m),
令y=0,得x2+(m﹣2)x﹣2m=0,解得:x1=2,x2=﹣m,
∴A(﹣m,0),B(2,0),
∴AB=2﹣(﹣m)=m+2,OC=2m
∵S△ABC=3
∴(m+2)?2m=3,解得:m1=1,m2=﹣3(不符合题意)
∴m=1;
∴抛物线C1:y=x2﹣x﹣2
(2)如图2,设D(t,t2﹣t﹣2),CD交x轴于K,作DT⊥x轴于T,
由(1)得:B(2,0),C(0,﹣2)
∵当x轴恰好三等分△DBC的面积时,有S△BDK=S△BCD或S△BDK=S△BCD
∴=或=,
①当=时,=
∴DT=OC
∴t2﹣t﹣2=×2,解得:t1=,t2=,
∵点D在第二象限,
∴t<0
∴t=,
②当=时,=2
∴DT=2OC
∴t2﹣t﹣2=2×2,解得:t1=3,t2=﹣2,
∵t<0
∴t=﹣2
综上所述,当x轴恰好三等分△DBC的面积时,点D的横坐标为或﹣2;
(3)如图3,取WE中点T,过点T作TR⊥EF交EN于点R,连接WR,WN,
由题意知:抛物线C1:y=x2﹣x﹣2=﹣,将抛物线C1向右平移,使新抛物线C2经过原点,
∴新抛物线C2解析式为y=(x﹣)2﹣=x2﹣3x,对称轴为:直线x=,顶点E(,﹣),
∴F(,4),EF=
在y=x2﹣3x中,令y=4,则4=x2﹣3x,解得:x1=﹣1,x2=4
∴G(﹣1,4),H(4,4)
∴GH=5
∵GM=NH=t,WF=,
∴MF=NF=﹣t,WE=﹣=5,WT=TE=WE=,
∵∠EFM=∠EFN=90°,WF=NF
∴△MWF≌△NWF(SAS)
∴∠MWF=∠NWF
∵∠MWF=3∠FEN
∴∠NWF=3∠FEN
∵∠NWF=∠FEN+∠ENW
∴∠ENW=2∠FEN
∵WT=ET,TR⊥EF
∴RW=RE
∴∠FEN=∠EWR
∴∠NRW=2∠FEN
∴∠ENW=∠NRW
∴RW=WN
∴RE=WN
由勾股定理得:EN2=EF2+NF2=+,WN2=WF2+NF2=+,
∵△ERT∽△ENF
∴=,即ER=EN
∴ER2=EN2=[+],
∴[+]=+,
解得:t1=(不符合题意,舍去),t2=,
故t=(秒).
同课章节目录
