2020-2021学年七年级数学人教版下册《5.3.1 平行线的性质》练习题 (Word版 无答案)
文档属性
| 名称 | 2020-2021学年七年级数学人教版下册《5.3.1 平行线的性质》练习题 (Word版 无答案) | 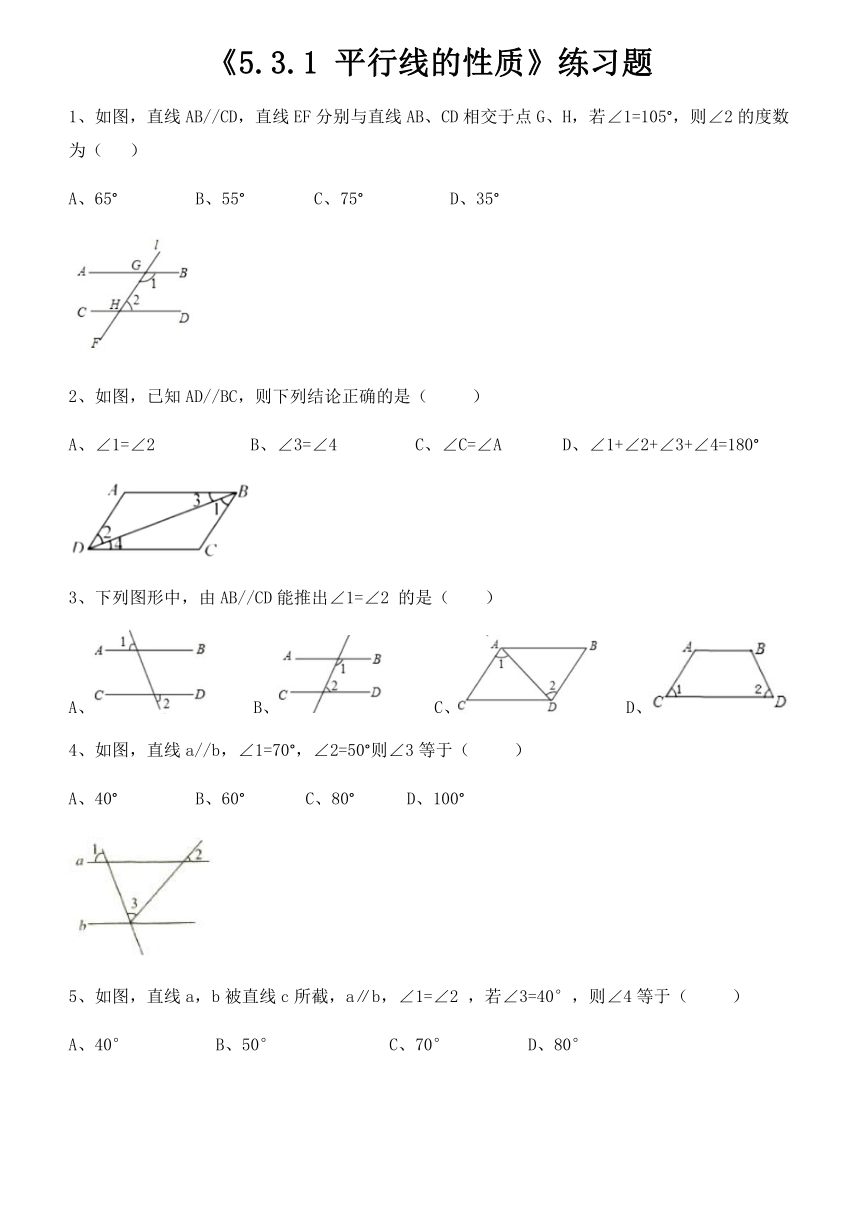 | |
| 格式 | docx | ||
| 文件大小 | 470.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-20 09:30:45 | ||
图片预览


文档简介
《5.3.1
平行线的性质》练习题
如图,直线AB//CD,直线EF分别与直线AB、CD相交于点G、H,若∠1=105°,则∠2的度数为(
)
65°
B、55°
C、75°
D、35°
如图,已知AD//BC,则下列结论正确的是(
)
A、∠1=∠2
B、∠3=∠4
C、∠C=∠A
D、∠1+∠2+∠3+∠4=180°
3、下列图形中,由AB//CD能推出∠1=∠2
的是(
)
A、
B、
C、
D、
4、如图,直线a//b,∠1=70°,∠2=50°则∠3等于(
)
A、40°
B、60°
C、80°
D、100°
如图,直线a,b被直线c所截,a∥b,∠1=∠2
,若∠3=40°,则∠4等于(
)
40°
B、50°
C、70°
D、80°
下列说法正确的是(
)
两直线被第三条直线所截的同位角相等
B、两直线被第三条直线所截的同旁内角互补
C、两平行线被第三条直线所截的同位角的平分线互相垂直
D、两平行线被第三条直线所截的同旁内角的平分线互相垂直
如图AB//CD,直线EF分别交AB,CD于E,F两点,∠BEF的平分线交CD于点G,若∠EFG=72°,则∠EGF等于(
)
36°
B、54°
C、72°
D、108°
如图,已知直线//,则∠是(
)
A、150°
B、140°
C、130°
D、120°
如图,已知AB//CD,CE平分∠ACD,如果∠1=25°,那么∠2的度数是(
)。
A、160°
B、50°
C、70°
D、60°
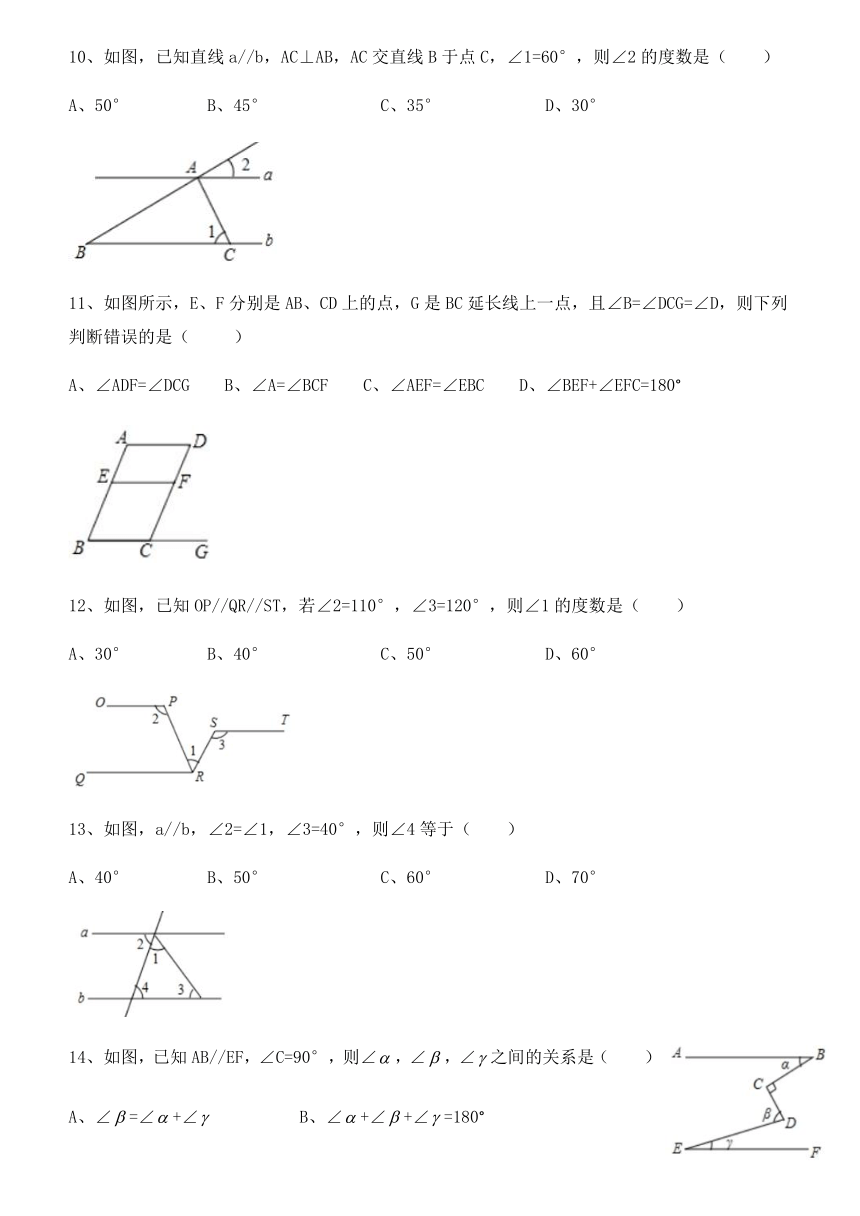
如图,已知直线a//b,AC⊥AB,AC交直线B于点C,∠1=60°,则∠2的度数是(
)
A、50°
B、45°
C、35°
D、30°
如图所示,E、F分别是AB、CD上的点,G是BC延长线上一点,且∠B=∠DCG=∠D,则下列判断错误的是(
)
∠ADF=∠DCG
B、∠A=∠BCF
C、∠AEF=∠EBC
D、∠BEF+∠EFC=180°
如图,已知OP//QR//ST,若∠2=110°,∠3=120°,则∠1的度数是(
)
A、30°
B、40°
C、50°
D、60°
如图,a//b,∠2=∠1,∠3=40°,则∠4等于(
)
A、40°
B、50°
C、60°
D、70°
如图,已知AB//EF,∠C=90°,则∠,∠,∠之间的关系是(
)
∠=∠+∠
B、∠+∠+∠=180°
C、∠+∠-∠=90°
D、∠+∠-∠=90°
如图,已知//,⊥,∠1=44°,∠2的度数为(
)。
A、46°
B、44°
C、36°
D、22°
如图,直线、,交于一点,直线//,∠1=120°,∠2=65°,则∠3的度数为(
)。
A、60°
B、55°
C、46°
D、65°
直线a,b,c,d的位置如图所示,如果∠1=80°,∠2=80°,∠3=70°,那么∠4等于
。
如图,已知AB//CD,且∠ABE=120°,∠CDE=30°,则∠BED的度数是
如图,已知直线a//b,将三角板的直角顶点放在直线b上,∠1=35°,∠2=
。
如图,直线a,b被直线c所截,若a//b,则∠1+∠2的度数是
。
21、如图所示,AB//CD(已知)
∠ABC=
(
),
//
(两直线平分,内错角相等)
∠BCD+
=180°(
)
∠3=∠4(已知)
//
(
)
∠FAD=∠FBC(已知)
//
(
)
22、如图,直线a//b,点B在直线b上,且AB⊥BC,∠1=65°,求∠2的度数。
如图,一只渔船A在海上航行,发现一小岛B,以渔船为观测点,测得小岛在船的北偏东50°方向上,那么在小岛上看这只船是什么方向?
24、如图所示,已知AB//CD,从图中发现∠B+∠E+∠D=360°,你知道为什么吗?应用你所学的知识来说明?
25、如图所示,在中,CD⊥AB于D,EF⊥AB与F,∠1=∠2.
求证:∠ADG=∠B
如图,已知CB⊥AB,CE平分∠BCD,DE平分∠CDA,∠1+∠2=90°.
求证:DA⊥AB.
平行线的性质》练习题
如图,直线AB//CD,直线EF分别与直线AB、CD相交于点G、H,若∠1=105°,则∠2的度数为(
)
65°
B、55°
C、75°
D、35°
如图,已知AD//BC,则下列结论正确的是(
)
A、∠1=∠2
B、∠3=∠4
C、∠C=∠A
D、∠1+∠2+∠3+∠4=180°
3、下列图形中,由AB//CD能推出∠1=∠2
的是(
)
A、
B、
C、
D、
4、如图,直线a//b,∠1=70°,∠2=50°则∠3等于(
)
A、40°
B、60°
C、80°
D、100°
如图,直线a,b被直线c所截,a∥b,∠1=∠2
,若∠3=40°,则∠4等于(
)
40°
B、50°
C、70°
D、80°
下列说法正确的是(
)
两直线被第三条直线所截的同位角相等
B、两直线被第三条直线所截的同旁内角互补
C、两平行线被第三条直线所截的同位角的平分线互相垂直
D、两平行线被第三条直线所截的同旁内角的平分线互相垂直
如图AB//CD,直线EF分别交AB,CD于E,F两点,∠BEF的平分线交CD于点G,若∠EFG=72°,则∠EGF等于(
)
36°
B、54°
C、72°
D、108°
如图,已知直线//,则∠是(
)
A、150°
B、140°
C、130°
D、120°
如图,已知AB//CD,CE平分∠ACD,如果∠1=25°,那么∠2的度数是(
)。
A、160°
B、50°
C、70°
D、60°
如图,已知直线a//b,AC⊥AB,AC交直线B于点C,∠1=60°,则∠2的度数是(
)
A、50°
B、45°
C、35°
D、30°
如图所示,E、F分别是AB、CD上的点,G是BC延长线上一点,且∠B=∠DCG=∠D,则下列判断错误的是(
)
∠ADF=∠DCG
B、∠A=∠BCF
C、∠AEF=∠EBC
D、∠BEF+∠EFC=180°
如图,已知OP//QR//ST,若∠2=110°,∠3=120°,则∠1的度数是(
)
A、30°
B、40°
C、50°
D、60°
如图,a//b,∠2=∠1,∠3=40°,则∠4等于(
)
A、40°
B、50°
C、60°
D、70°
如图,已知AB//EF,∠C=90°,则∠,∠,∠之间的关系是(
)
∠=∠+∠
B、∠+∠+∠=180°
C、∠+∠-∠=90°
D、∠+∠-∠=90°
如图,已知//,⊥,∠1=44°,∠2的度数为(
)。
A、46°
B、44°
C、36°
D、22°
如图,直线、,交于一点,直线//,∠1=120°,∠2=65°,则∠3的度数为(
)。
A、60°
B、55°
C、46°
D、65°
直线a,b,c,d的位置如图所示,如果∠1=80°,∠2=80°,∠3=70°,那么∠4等于
。
如图,已知AB//CD,且∠ABE=120°,∠CDE=30°,则∠BED的度数是
如图,已知直线a//b,将三角板的直角顶点放在直线b上,∠1=35°,∠2=
。
如图,直线a,b被直线c所截,若a//b,则∠1+∠2的度数是
。
21、如图所示,AB//CD(已知)
∠ABC=
(
),
//
(两直线平分,内错角相等)
∠BCD+
=180°(
)
∠3=∠4(已知)
//
(
)
∠FAD=∠FBC(已知)
//
(
)
22、如图,直线a//b,点B在直线b上,且AB⊥BC,∠1=65°,求∠2的度数。
如图,一只渔船A在海上航行,发现一小岛B,以渔船为观测点,测得小岛在船的北偏东50°方向上,那么在小岛上看这只船是什么方向?
24、如图所示,已知AB//CD,从图中发现∠B+∠E+∠D=360°,你知道为什么吗?应用你所学的知识来说明?
25、如图所示,在中,CD⊥AB于D,EF⊥AB与F,∠1=∠2.
求证:∠ADG=∠B
如图,已知CB⊥AB,CE平分∠BCD,DE平分∠CDA,∠1+∠2=90°.
求证:DA⊥AB.
