2021年九年级中考数学复习《探索二次函数综合型压轴题解题技巧》分类训练六:与平行四边形相关的压轴题(word版含答案)
文档属性
| 名称 | 2021年九年级中考数学复习《探索二次函数综合型压轴题解题技巧》分类训练六:与平行四边形相关的压轴题(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 625.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-20 10:20:17 | ||
图片预览




文档简介
2021中考数学复习《探索二次函数综合型压轴题解题技巧》分类训练六:
与平行四边形相关的压轴题(附答案)
方法提炼:
1、特殊四边形的探究问题解题方法步骤如下:(1)先假设结论成立;(2)设出点坐标,求边长.(类型一方法指导);(3)建立关系式,并计算。若四边形的四个顶点位置已确定,则直接利用四边形边的性质进行计算;若四边形的四个顶点位置不确定,需分情况讨论。
2、 探究平行四边形:①以已知边为平行四边形的某条边,画出所有的符合条件的图形后,利用平行四边形的对边相等进行计算;②以已知边为平行四边形的对角线,画出所有的符合条件的图形后,利用平行四边形对角线互相平分的性质进行计算;③若平行四边形的各顶点位置不确定,需分情况讨论,常以已知的一边作为一边或对角线分情况讨论。
典例引领:
例:如图所示:已知抛物线y=ax2(a≠0)与一次函数y=kx+b的图象相交于两点A(﹣1,﹣1),B(2,﹣4),点P是抛物线上不与A,B重合的一个动点,点Q是y轴上的一个动点.
(1)求a,k,b的值.
(2)直接写出关于x的不等式ax2<kx﹣2的解集;
(3)当点P在直线AB上方时,请求出△PAB面积的最大值并求出此时点P的坐标;
(4)是否存在以P,Q,A,B为顶点的四边形是平行四边形?若存在,请直接写出P,Q的坐标;若不存在,请说明理由.
分析:(1)根据待定系数法得出a,k,b的值;
(2)观察函数图象,即可得出不等式的解集;
(3)过点A作y轴的平行线,过点B作x轴的平行线,两者交于点C,连接PC.根据三角形的面积公式解答即可;
(4)根据平行四边形的性质和坐标特点解答即可.
解:(1)把A(﹣1,﹣1),代入y=ax2中,可得:a=﹣1,
把A(﹣1,﹣1),B(2,﹣4)代入y=kx+b中,可得:,解得,
∴a=﹣1,k=﹣1,b=﹣2;
(2)观察函数图象可知,关于x的不等式ax2<kx﹣2的解集是x<﹣1或x>2;
(3)过点A作y轴的平行线,过点B作x轴的平行线,两者交于点C,
∵A(﹣1,﹣1),B(2,﹣4),
∴C(﹣1,﹣4),AC=BC=3,
设点P的横坐标为m,则点P的纵坐标为﹣m2.
过点P作PD⊥AC于D,作PE⊥BC于E.则D(﹣1,﹣m2),E(m,﹣4),
∴PD=m+1,PE=﹣m2+4.
∴S△APB=S△APC+S△BPC﹣S△ABC,
=×AC?PD+×BC?PE﹣×BC?AC,
=×3×(m+1)×3×(﹣m2+4)﹣×3×3,
=﹣m2+m+3.
∵﹣<0,m=﹣=,
而﹣1<m<2,
∴当m=时,S△APB的最大值为,此时点P的坐标为(,﹣);
(4)存在三组符合条件的点.
当以P,Q,A,B为顶点的四边形是平行四边形时,
∵AP=BQ,AQ=BP,A(﹣1,﹣1),B(2,﹣4),
可得坐标如下:
①P′的横坐标为﹣3,代入二次函数表达式,
解得:P'(﹣3,﹣9),Q'(0,﹣12);
②P″的横坐标为3,代入二次函数表达式,
解得:P″(3,﹣9),Q″(0,﹣6);
③P的横坐标为1,代入二次函数表达式,
解得:P(1,﹣1),Q(0,﹣4).
故:P、Q的坐标分别为(﹣3,﹣9)、(0,﹣12)或(3,﹣9)、(0,﹣6)或(1,﹣1)、(0,﹣4).
点评:主要考查了二次函数的解析式的求法和与几何图形结合的综合能力的培养.要会利用数形结合的思想把代数和几何图形结合起来,利用点的坐标的意义表示线段的长度,从而求出线段之间的关系.
跟踪训练:
1.已知,如图,抛物线y=ax2+bx+c(a≠0)的顶点为M(1,9),经过抛物线上的两点A(﹣3,﹣7)和B(3,m)的直线交抛物线的对称轴于点C.
(1)求抛物线的解析式和直线AB的解析式.
(2)在抛物线上A、M两点之间的部分(不包含A、M两点),是否存在点D,使得S△DAC=2S△DCM?若存在,求出点D的坐标;若不存在,请说明理由.
(3)若点P在抛物线上,点Q在x轴上,当以点A,M,P,Q为顶点的四边形是平行四边形时,直接写出满足条件的点P的坐标.
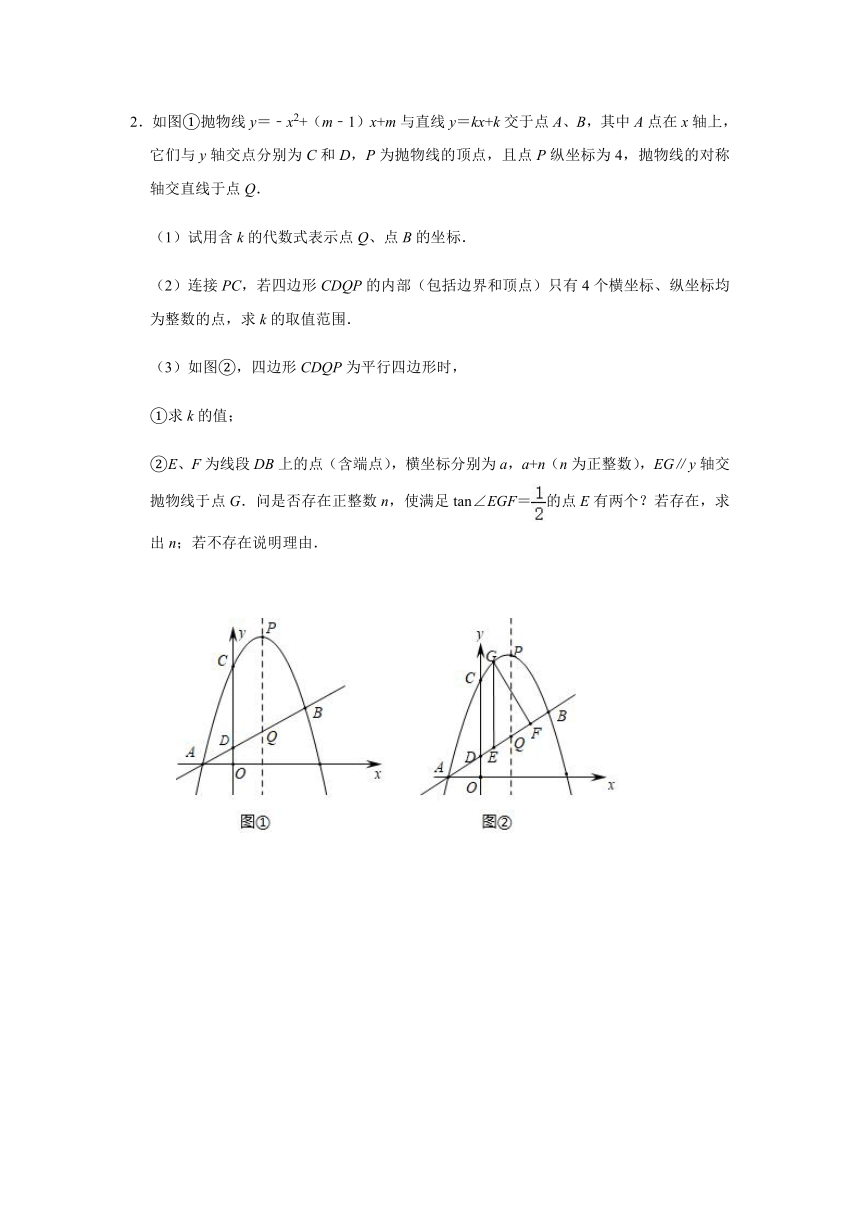
2.如图①抛物线y=﹣x2+(m﹣1)x+m与直线y=kx+k交于点A、B,其中A点在x轴上,它们与y轴交点分别为C和D,P为抛物线的顶点,且点P纵坐标为4,抛物线的对称轴交直线于点Q.
(1)试用含k的代数式表示点Q、点B的坐标.
(2)连接PC,若四边形CDQP的内部(包括边界和顶点)只有4个横坐标、纵坐标均为整数的点,求k的取值范围.
(3)如图②,四边形CDQP为平行四边形时,
①求k的值;
②E、F为线段DB上的点(含端点),横坐标分别为a,a+n(n为正整数),EG∥y轴交抛物线于点G.问是否存在正整数n,使满足tan∠EGF=的点E有两个?若存在,求出n;若不存在说明理由.
3.如图,在平面直角坐标系中,抛物线y=x2+4x的顶点为点A
(1)求点A的坐标;
(2)点B为抛物线上横坐标等于﹣6的点,点M为线段OB的中点,点P为直线OB下方抛物线上的一动点.当△POM的面积最大时,过点P作PC⊥y轴于点C,若在坐标平面内有一动点Q满足PQ=,求OQ+QC的最小值;
(3)当(2)中OQ+QC取得最小值时,直线OQ与抛物线另一交点为点E,作点E关于抛物线对称轴的对称点E’.点R是抛物线对称轴上的一点,在x轴上是否存在点S,使得以O、E′、R、S为顶点的四边形是平行四边形?若存在,请直接写出S点的坐标;若不存在,请说明理由.
4.综合与探究:
如图,抛物线y=x2﹣x﹣2,与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C抛物线的对称轴为l.
(1)求点A,B,C的坐标;
(2)若点D是第一象限内抛物线上一点,过点D作DE⊥x轴于点E,交直线BC于点F,当OE=4DF时,求四边形DOBF的面积;
(3)在(2)的条件下,若点M在抛物线上,点N在抛物线的对称轴上,是否存在以点B,D,M,N为顶点的四边形是平行四边形?若存在,请求出所有符合条件的点M的坐标;若不存在,请说明理由.
5.如图,在平面直角坐标系中,把抛物线y=x2先向右平移1个单位长度,再向下平移4个单位长度,得到抛物线y=(x﹣h)2+k,所得抛物线与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,顶点为M.
(1)写出h、k的值及点A、B的坐标;
(2)判断△BCM的形状,并计算其面积;
(3)点P是抛物线上的一动点,在y轴上存在点Q,使以点A、B、P、Q为顶点组成的四边形是平行四边形,求点P的坐标.
6.如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(﹣1,0),C(2,3)两点,与y轴交于点N,其顶点为D.
(1)求抛物线及直线AC的函数关系式;
(2)若P是抛物线上位于直线AC上方的一个动点,设点P的横坐标为t;
①当S△ACP=S△ACN时,求点P的坐标;
②是否存在点P,使得△ACP是以AC为斜边的直角三角形?若存在,求点P的坐标;若不存在,请说明理由;
(3)若抛物线的对称轴与直线AC相交于点B,E为直线AC上的任意一点,过点E作EF∥BD交抛物线于点F,以B,D,E,F为顶点的四边形能否为平行四边形?若能,请直接写出点E的坐标;若不能,请说明理由.
7.如图,抛物线y=与x轴分别交于A、B两点(点A在点B的左侧,)与y轴交于点C,作直线AC.
(1)点B的坐标为 ,直线AC的关系式为 .
(2)设在直线AC下方的抛物线上有一动点P,过点P作PD⊥x轴于D,交直线AC于点E,当CE平分∠OEP时求点P的坐标.
(3)点M在x轴上,点N在抛物线上,试问以点A、C、M、N为顶点的四边形能否成为平行四边形?若存在,直接写出所有点M的坐标;若不存在,请简述你的理由.
8.如图,直线y=﹣x+2与x轴交于点A,与y轴交于点B,抛物线y=﹣+bx+c经过A,B两点.
(1)求抛物线的解析式;
(2)点P在抛物线上,点Q在直线AB上,当P,Q关于原点O成中心对称时,求点Q的坐标;
(3)点M为直线AB上的动点,点N为抛物线上的动点,当以点O、B、M、N为顶点的四边形是平行四边形时,请直接写出点M的坐标.
9.如图,已知直线y=﹣x+2与两坐标轴分别交于A、B两点,抛物线y=﹣x2+bx+c经过点A、B,点P为直线AB上的一个动点,过P作y轴的平行线与抛物线交于C点,抛物线与x轴另一个交点为D.
(1)求图中抛物线的解析式;
(2)当点P在线段AB上运动时,求线段PC的长度的最大值;
(3)在直线AB上是否存在点P,使得以O、A、P、C为顶点的四边形是平行四边形?若存在,请求出此时点P的坐标,若不存在,请说明理由.
10.如图,在平面直角坐标系中,抛物线y=ax2+bx+c与两坐标轴分别交于点A、B、C,直线y=﹣x+4经过点B,与y轴交点为D,M(3,﹣4)是抛物线的顶点.
(1)求抛物线的解析式.
(2)已知点N在对称轴上,且AN+DN的值最小.求点N的坐标.
(3)在(2)的条件下,若点E与点C关于对称轴对称,请你画出△EMN并求它的面积.
(4)在(2)的条件下,在坐标平面内是否存在点P,使以A、B、N、P为顶点的四边形是平行四边形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
11.如图,抛物线过A(1,0)、B(﹣3,0),C(0,﹣3)三点,直线AD交抛物线于点D,点D的横坐标为﹣2,点P(m,n)是线段AD上的动点,过点P的直线垂直于x轴,交抛物线于点Q.
(1)求直线AD及抛物线的解析式;
(2)求线段PQ的长度l与m的关系式,m为何值时,PQ最长?
(3)在平面内是否存在整点(横、纵坐标都为整数)R,使得P、Q、D、R为顶点的四边形是平行四边形?若存在,求出点R的坐标;若不存在,说明理由.
12.如图所示,抛物线y=x2+bx+c经过点A(2,﹣3)与C(0,﹣3),与x轴负半轴的交点为B.
(1)求抛物线的解析式与点B坐标;
(2)若点D在x轴上,使△ABD是等腰三角形,求所有满足条件的点D的坐标;
(3)点M在抛物线上,点N在抛物线的对称轴上,若以A、B、M、N为顶点的四边形是平行四边形,其中AB∥MN,请直接写出所有满足条件的点M的坐标.
参考答案
1.分析:(1)二次函数表达式为:y=a(x﹣1)2+9,即可求解;
(2)S△DAC=2S△DCM,则S△DAC=DH(xC﹣xA)=(﹣x2+2x+8﹣2x+1)(1+3)=(9﹣1)(1﹣x)×2,即可求解;
(3)分AM是平行四边形的一条边、AM是平行四边形的对角线两种情况,分别求解即可.
解:(1)二次函数表达式为:y=a(x﹣1)2+9,
将点A的坐标代入上式并解得:a=﹣1,
故抛物线的表达式为:y=﹣x2+2x+8…①,
则点B(3,5),
将点A、B的坐标代入一次函数表达式并解得:
直线AB的表达式为:y=2x﹣1;
(2)存在,理由:
二次函数对称轴为:x=1,则点C(1,1),
过点D作y轴的平行线交AB于点H,
设点D(x,﹣x2+2x+8),点H(x,2x﹣1),
∵S△DAC=2S△DCM,
则S△DAC=DH(xC﹣xA)=(﹣x2+2x+8﹣2x+1)(1+3)=(9﹣1)(1﹣x)×2,
解得:x=﹣1或5(舍去5),
故点D(﹣1,5);
(3)设点Q(m,0)、点P(s,t),t=﹣s2+2s+8,
①当AM是平行四边形的一条边时,
点M向左平移4个单位向下平移16个单位得到A,
同理,点Q(m,0)向左平移4个单位向下平移16个单位为(m﹣4,﹣16),即为点P,
即:m﹣4=s,﹣16=t,而t=﹣s2+2s+8,
解得:s=6或﹣4,
故点P(6,﹣16)或(﹣4,﹣16);
②当AM是平行四边形的对角线时,
由中点公式得:m+s=﹣2,t=2,而t=﹣s2+2s+8,
解得:s=1,
故点P(1,2)或(1﹣,2);
综上,点P(6,﹣16)或(﹣4,﹣16)或(1,2)或(1﹣,2).
点评:本题考查的是二次函数综合运用,涉及到一次函数、平行四边形性质、图形的面积计算等,其中(3),要注意分类求解,避免遗漏.
2.分析:(1)由图可知,抛物线对称轴在y轴右侧,顶点P纵坐标为4,用顶点坐标公式即列得关于m的不等式和方程,求解即得到m的值,进而得到抛物线解析式.把顶点P的横坐标代入直线y=kx+k即得到用k表示点Q的坐标.令抛物线解析式为0,解方程求得点A坐标.把直线与抛物线解析式联立方程组并整理得关于x的一元二次方程,利用韦达定理得xA+xB的值,把xA代入即求得点B横坐标进而求得B的纵坐标.
(2)由(1)得C(0,3),P(1,4),即四边形CDQP的内部(包括边界和顶点)有2个满足横坐标、纵坐标均为整数的点P、C,另外两个满足的点应该是M(0,2)、N(1,3),由图象可知此时点D在线段MS上(不与S(0,1)重合),点Q在线段NR上(不与点R(1,2)重合).因为D(0,k),Q(1,2k),即列得关于k的不等式组,求解即得到k的取值范围.
(3)①求直线CP解析式,由四边形CDQP为平行四边形可得DQ∥CP,即直线y=kx+k的k与直线CP解析式的一次项系数相等,求得k=1.
②过点F作FH⊥⊥EG于点H,则Rt△FGH中,tan∠EGF=,即GH=2FH.由点E、F横坐标分别为a,a+n,可用含a、n的式子表示FH、GH的长,代入GH=2FH,得到关于a的一元二次方程(n为常数).因为满足tan∠EGF=的点E有两个,即关于a的方程有两个不相等的实数根,由△>0求得n的取值范围小于0,故不存在满足条件的正整数n.
解:(1)∵抛物线y=﹣x2+(m﹣1)x+m的顶点P纵坐标为4
∴=4
解得:m1=3,m2=﹣5
∵抛物线对称轴在y轴右侧
∴﹣>0
解得:m>1
∴m=3
∴抛物线为y=﹣x2+2x+3,顶点P(1,4)
∵直线y=kx+k与对称轴交于点Q
∴Q(1,2k)
∵y=﹣x2+2x+3=0时,解得:x1=﹣1,x2=3
∴A(﹣1,0)
∵ 整理得:x2+(k﹣2)x+k﹣3=0
∴xA+xB=﹣(k﹣2)
∴xB=﹣(k﹣2)﹣xA=﹣(k﹣2)﹣(﹣1)=﹣k+3
∴yB=k?xB+k=﹣k2+4k
∴B(﹣k+3,﹣k2+4k)
(2)∵C(0,3),P(1,4),D(0,k),Q(1,2k)
∴当四边形CDQP的内部(包括边界和顶点)只有4个横坐标、纵坐标均为整数的点时,
4个点是C、P、M(0,2)、N(1,3)(如图1)
∴点D在线段MS上(不与S(0,1)重合),点Q在线段NR上(不与点R(1,2)重合)
∴
解得:1<k≤
(3)①∵C(0,3),P(1,4)
∴直线CP解析式为y=x+3
∵四边形CDQP为平行四边形
∴DQ∥CP,即直线y=kx+k平行直线CP
∴k=1
②不存在满足条件的正整数n.
如图2,过点F作FH⊥EG于点H
∴∠FHE=∠FHG=90°
∵k=1
∴直线AB:y=x+1
∵点E在线段DB上横坐标为a,EG∥y轴交抛物线于点G
∴E(a,a+1),G(a,﹣a2+2a+3)
∵点F在线段DB上横坐标为a+n
∴FH=xF﹣xE=n,F(a+n,a+n+1)
∴GH=yG﹣yF=﹣a2+2a+3﹣(a+n+1)=﹣a2+a+2﹣n
∵Rt△FGH中,tan∠EGF=
∴GH=2FH
∴﹣a2+a+2﹣n=2n,整理得:a2﹣a+3n﹣2=0
∵满足tan∠EGF=的点E有两个,
∴关于a的方程a2﹣a+3n﹣2=0有两个不相等的实数根
∴△=1﹣4(3n﹣2)>0
解得:0<n<
∴不存在正整数n,使满足tan∠EGF=的点E有两个
点评:本题考查了二次函数的图象与性质,一元二次方程的解法及根与系数的关系,一元一次不等式的解法,一次函数的图象与性质,三角函数的应用.第(2)题的解题关键是先确定满足条件的4个点中包含C、P,把另外两个横、纵坐标均为整数的点确定下来,再根据直线的位置确定k的取值范围.
3.分析:(1)配方法将抛物线解析式化为顶点式即可;
(2)待定系数法求直线AB解析式为y=﹣2x,设P(m,m2+4m),则H(m,﹣2m),PH=﹣2m﹣(m2+4m)=﹣m2﹣6m,由△PGH∽△MDO可得 PG?MO=PH?MD=3(﹣m2﹣6m)=﹣3m2﹣18m,从而得:S△POM=PG?MO=﹣9m=﹣(m+3)2+,求得P(﹣3,﹣3),在PC上取点T,使得PT=,连接QT,OT,由△QPT∽△CPQ可得TQ=QC,进而可求得OQ+QC的最小值为;
(3)先根据OQ+QC取得最小值时,点O、Q、T三点共线,求得T(,﹣3),待定系数法求得直线OQ解析式为y=x,解方程组可求得点E的坐标,进而可求得E′的坐标,根据以O、E′、R、S为顶点的四边形是平行四边形,分三种情形:①OR为对角线,②OS为对角线,③OE′为对角线,分别求出对应的点S坐标即可.
解:(1)∵y=x2+4x=(x+2)2﹣4,
∴A(﹣2,﹣4);
(2)如图1,过P作PH⊥x轴交OB于H,作PG⊥BC于G,过M作MD⊥y轴交y轴于D,
∵点B为抛物线上横坐标等于﹣6的点,∴B(﹣6,12),
∴直线AB解析式为y=﹣2x
设P(m,m2+4m),则H(m,﹣2m),PH=﹣2m﹣(m2+4m)=﹣m2﹣6m
∵点M为线段OB的中点,∴M(﹣3,6),∴MD=3
∵PH∥y轴
∴∠PHG=∠MOD
∵PG⊥BC MD⊥y轴
∴∠PGH=∠MDO
∴△PGH∽△MDO
∴=,即 PG?MO=PH?MD=3(﹣m2﹣6m)=﹣3m2﹣18m,
∴S△POM=PG?MO=﹣9m=﹣(m+3)2+
∵﹣<0,∴当m=﹣3时,S△POM的值最大,此时P(﹣3,﹣3),
在PC上取点T,使得PT=,连接QT,OT,
∵PC=3,PQ=
∴==
∵∠QPT=∠CPQ
∴△QPT∽△CPQ
∴==,即TQ=QC,
∴OQ+QC=OQ+TQ≥OT
∵OT===
∴OQ+QC的最小值为;
(3)∵当(2)中OQ+QC取得最小值时,点O、Q、T三点共线,T(,﹣3)
∴直线OQ解析式为y=x,
解方程组得,
∴E(,),∵抛物线对称轴为直线x=﹣2,
∴E′(﹣,),
以O、E′、R、S为顶点的四边形是平行四边形,分以下三种情形:
①OR为对角线,∵OE′RS是平行四边形
∴OS∥E′R,OS=E′R=,∴S1 (,0)
②OS为对角线,∵OE′RS是平行四边形
∴OE′∥RS,R(﹣2,),∴S2(,0)
③OE′为对角线,∵OE′RS是平行四边形
∴OS∥E′R,OS=E′R=,∴S3(,0),
综上所述,点S的坐标为:S1 (,0),S2(,0),S3(,0).
点评:本题考查二次函数性质,用待定系数法求一次函数的解析式,图形的平移和对称,一元二次方程的解法,相似三角形的判定和性质,分类讨论思想.第(2)问关键是通过相似三角形转化为两点之间距离最短的问题,第(3)问的关键是分类讨论.
4.分析:(1)把x=0代入抛物线解析式求得y即得到点C坐标;令y=0解方程即求得点A、B坐标.
(2)设点D横坐标为d,用d表示OE、DE的长;求直线BC解析式,用d表示点F坐标,进而用d表示DF的长.根据OE=4DF列方程,求解得点D坐标,即得到各线段的长.由图可知,四边形DOBF面积等于△AED与△BEF面积之差,直接计算即可.
(3)先求出对称轴为直线x=1.以BD为平行四边形的边或对角线进行分类:若BD为边,画出相应的图形,根据平移性质得到点M的横坐标,代入解析式求纵坐标;以BD为对角线,BD与MN互相平分,则BD中点与MN中点相同,利用中点坐标公式列方程即求出点M坐标.
解:(1)当y=x2﹣x﹣2=0时,
解得:x1=﹣2,x2=4
∴A(﹣2,0),B(4,0)
当x=0时,y=x2﹣x﹣2=﹣2
∴C(0,﹣2)
(2)∵点D是第一象限内抛物线上的点
∴设点D坐标为(d,d2﹣d﹣2)(d>4)
∵DE⊥x轴于点E
∴OE=d,DE=d2﹣d﹣2
设直线BC解析式为y=kx﹣2
把点B代入得:4k﹣2=0,解得:k=
∴直线BC:y=x﹣2
∵DE交BC于点F
∴F(d,d﹣2)
∴DF=d2﹣d﹣2﹣(d﹣2)=d2﹣d
∵OE=4DF
∴d=4(d2﹣d)
解得:d1=0(舍去),d2=5
∴D(5,),F(5,)
∴DE=,EF=,BE=OE﹣OB=5﹣4=1
∴S四边形DOBF=S△AED﹣S△BEF=AE?DE﹣BE?EF=×5×﹣×1×=
(3)存在以点B,D,M,N为顶点的四边形是平行四边形
∵A(﹣2,0),B(4,0)
∴对称轴为直线:x==1
∴xN=1
①如图1,BD∥MN,四边形BMND是平行四边形
∴DN∥BM,DN=BM
∴DN向下平移个单位,向左平移1个单位可得BM
∴xM=xN﹣1=0
∴M(0,﹣2)
②如图2,BD∥MN,四边形BDMN是平行四边形
∴DM∥BN,DM=BN
∴BN向上平移个单位,向右平移1个单位可得DM
∴xM=xN+1=2
∴M(2,﹣2)
③以BD为对角线时,BD与MN互相平分
∴BD中点与MN中点相同
∴
设M(m,m2﹣m﹣2),N(1,n)
∴ 解得:
∴M(8,10)
综上所述,符合条件的点M的坐标为(0,﹣2)或(2,﹣2)或(8,10).
点评:本题考查了二次函数的图象与性质,一元二次方程的解法,平行四边形的性质,平移的性质.平行四边形存在性问题中,已知两个顶点时,以此线段为平行四边形的边或对角线进行分类讨论画图并计算;其中固定线段为边长求另外两点时,可利用平移性质求点坐标之间的关系.
5.分析:解:(1)抛物线y=x2先向右平移1个单位长度,再向下平移4个单位长度,得到抛物线y=(x﹣1)2﹣4,
故h=1,k=﹣4,
y=(x﹣1)2﹣4=x2﹣2x﹣3,令y=0,则x=3或﹣1,
即点A、B的坐标分别为(﹣1,0)、(3,0);
(2)点M的坐标为(1,﹣4),
则BC=3,CM=,BM=,
故MB2=BC2+CM2,
故为直角三角形,其面积等于×CM×BC=3=3;
(3)①当AB是平行四边形的一条边时,
即PQ=AB=4,即x=±4,
把x=±4代入函数表达式得:y=5或21,
故点P(4,5)或(﹣4,21);
②当AB是平行四边形的对角线时,
设点P的横坐标为m,点Q的坐标为(0,n),
则AB的中点即为PQ的中点,则m+0=3﹣1,
解得:m=2,故点P(2,﹣3);
综上,点P的坐标为P(4,5)或(﹣4,21)或(2,﹣3).
解:(1)抛物线y=x2先向右平移1个单位长度,再向下平移4个单位长度,得到抛物线y=(x﹣1)2﹣4,
故h=1,k=﹣4,
y=(x﹣1)2﹣4=x2﹣2x﹣3,令y=0,则x=3或﹣1,
即点A、B的坐标分别为(﹣1,0)、(3,0);
(2)点M的坐标为(1,﹣4),
则BC=3,CM=,BM=,
故MB2=BC2+CM2,
故为直角三角形,其面积等于×CM×BC=3=3;
(3)①当AB是平行四边形的一条边时,
即PQ=AB=4,即x=±4,
把x=±4代入函数表达式得:y=5或21,
故点P(4,5)或(﹣4,21);
②当AB是平行四边形的对角线时,
设点P的横坐标为m,点Q的坐标为(0,n),
则AB的中点即为PQ的中点,则m+0=3﹣1,
解得:m=2,故点P(2,﹣3);
综上,点P的坐标为P(4,5)或(﹣4,21)或(2,﹣3).
点评:本题考查的是二次函数综合运用,涉及到平行四边形的性质、点的平移、中点的性质、面积的计算等,其中(3),要注意分类求解,避免遗漏.
6.分析:(1)运用待定系数法即可解决;
(2)①依题意得P(t,﹣t2+2t+3),过点P作PH⊥y轴于H,连接PN,由S△ACP=S△ACN可知PN∥AC,可得PH=HN,建立方程求解即可;②由△ACP是以AC为斜边的直角三角形,可得∠APC=90°,过P作PS⊥x轴于S,过C作CK⊥PS于K,可证△APS∽△PCK,根据相似三角形性质建立方程求解即可;
(3)运用配方法求顶点D坐标,由以B,D,E,F为顶点的四边形能为平行四边形,且EF∥BD,可得EF=BD,设点E(m,m+1),则F(m,﹣m2+2m+3),EF=,建立方程求解即可求得符合题意的点E坐标.
解:(1)将A(﹣1,0),C(2,3)代入y=﹣x2+bx+c中,得
,
解得
∴抛物线解析式为y=﹣x2+2x+3,
设直线AC解析式为y=mx+n,则
,
解得,
∴直线AC解析式为y=x+1;
(2)①在y=﹣x2+2x+3中,令x=0,得y=3,
∴N(0,3),
∵点P的横坐标为t;
∴P(t,﹣t2+2t+3),
过点P作PH⊥y轴于H,连接PN,设直线AC交y轴于G,则G(0,1),∠PHN=90°
∴OA=OG=1,PH=t,HN=OH﹣ON=﹣t2+2t,
∴∠AGO=∠CGN=45°
∵S△ACP=S△ACN
∴PN∥AC
∴∠PNH=∠CGN=45°
∴PH=HN
∴t=﹣t2+2t,解得:t1=0(舍去),t2=1,
∴P(1,4);
②如图2,过P作PS⊥x轴于S,过C作CK⊥PS于K,则∠CKP=∠PSA=90°
∵P(t,﹣t2+2t+3),A(﹣1,0),C(2,3),
∴CK=2﹣t,PK=﹣t2+2t,PS=﹣t2+2t+3,AS=t﹣(﹣1)=t+1,
∵△ACP是以AC为斜边的直角三角形
∴∠APS+∠CPK=∠APC=90°
∵∠PCK+∠CPK=90°
∴∠APS=∠PCK
∴△APS∽△PCK
∴=,即=
解得:t=
∵P是抛物线上位于直线AC上方的一个动点,
∴﹣1<t<2,但>2
∴t=
∴P(,).
(3)∵y=﹣x2+2x+3=﹣(x﹣1)2+4
∴顶点D(1,4)
∴B(1,2),BD=2,
以B,D,E,F为顶点的四边形能为平行四边形.
设点E(m,m+1),则F(m,﹣m2+2m+3),EF=,
∵EF∥BD
∴EF=BD
∴=2,解得:m1=0,m2=1(舍去),m3=,m4=;
∴点E的坐标为:(0,1)或(,)或(,).
点评:本题属于中考压轴题,与二次函数有关的代数几何综合题,涉及知识点多,综合性较强,难度较大,解题时必须熟练掌握并灵活运用相关性质和定理,还要注意数形结合,分类讨论;此题主要考查了二次函数图象和性质,待定系数法求函数解析式,三角形面积,直角三角形性质,平行四边形性质等.
7.分析:(1)y=,令y=0,则x=2或﹣8,令x=0,则y=﹣4,即可求解;
(2)证明△OEC为等腰三角形,OH2+HC2=OC2,即x2+4x2=16,解得:x=,EF=ECsinα=2××,故m=﹣,即可求解;
(3)①当AC是平行四边形的边时,则点A向右平移8个单位向下平移4个单位得到C,即可求解;②当AC是平行四边形的对角线时,利用中点公式即可求解.
解:(1)y=,令y=0,则x=2或﹣8,令x=0,则y=﹣4,
故点A、B、C的坐标分别为:(﹣8,0)、(2,0)、(0,﹣4),
将点A、C的坐标代入一次函数表达式:y=kx+b得:,解得:,
故直线AC的表达式为:y=﹣x﹣4,
故答案为:(2,0),y=﹣x﹣4;
(2)如图,左侧图是局部放大图,
∵CE平分∠OEP时,∴∠OEC=∠CEP,
∵PD∥y轴,∴∠CEP=∠ECO=∠OEC=α,
则△OEC为等腰三角形,
tan∠ECO==2=tanα,则sinα=,
过点E作y轴的垂线交于点F,过点O作OH⊥EC于点H,
设:OH=2x,则CH=x,而OH2+HC2=OC2,即x2+4x2=16,解得:x=,
EF=ECsinα=2××,故m=﹣,
则点P(﹣,﹣);
(3)设:点N(m,n),n=m2+m﹣4,点M(s,0),
①当AC是平行四边形的边时,
则点A向右平移8个单位向下平移4个单位得到C,
同理N(M)向右平移8个单位向下平移4个单位得到M(N),
即m+8=s,n﹣4=0或m﹣8=s,n+4=0,而n=m2+m﹣4,
解得:s=5±或﹣14,
②当AC是平行四边形的对角线时,
利用中点公式得:﹣8=m+s,﹣4=n,而n=m2+m﹣4,
解得:s=﹣2;
故点M的坐标为:(5+,0)或(5﹣)或(﹣14,0)或(﹣2,0).
点评:本题考查的是二次函数综合运用,涉及到平行四边形的性质、图形的平移、解直角三角形等,其中(3),要注意分类求解,避免遗漏.
8.分析:(1)先确定出点A,B坐标,再用待定系数法求出抛物线解析式;
(2)设点Q的作标为(x,y),则P点坐标是(﹣x,﹣y).利用直线方程与抛物线方程联立方程组,求得交点坐标即可;
(3)分OB为边和为对角线两种情况进行求解:①当OB为平行四边形的边时,用MN∥OB,表示和用MN=OB,建立方程求解;
②当OB为对角线时,OB与MN互相平分,交点为H,设出M,N坐标用OH=BH,MH=NH,建立方程组求解即可.
解:(1)∵与x轴交于点A,与y轴交于点B,
∴A(4,0),B(0,2).
∵抛物线经过点A,B,
∴,
∴,
∴抛物线的解析式为;
(2)设点Q的作标为(x,y),则P点坐标是(﹣x,﹣y),
∴,
解得:,;
∴.
(3))①当OB为平行四边形的边时,MN=OB=2,MN∥OB,
∵点M在直线AB上,点N为抛物线上,
∴设M(m,﹣m+2),
∴N(m,﹣m2+m+2),
∴MN=|﹣m2+m+2﹣(﹣m+2)|=|﹣m2+2m|=2,
Ⅰ、﹣m2+2m=2,
解得,m=2,
∴M(2,1),
Ⅱ、﹣m2+2m=2,
解得,m=2,
∴M(2﹣2),M(2+2,1﹣),
②当OB为对角线时,OB与MN互相平分,交点为H,
∴OH=BH,MH=NH,
∵B(0,2),O(0,0),
∴H(0,1),
设M(n,﹣),N(d,),
∴,
解得或,
∴M(﹣2+2,3﹣),M(﹣2﹣2,3+),
即:满足条件的点M的坐标为(2,1)或(2﹣2,1+)或(2+2,1﹣)或(﹣2+2,3﹣)或(﹣2﹣2,3+).
点评:此题是二次函数综合题,主要考查了待定系数法,平行四边形的性质,对称性,解本题的关键是求抛物线解析式,确定点M的坐标时,分类讨论是解本题的难点.
9.分析:(1)把x=0,y=0分别代入解析式可求点A,点B坐标,由待定系数法可求解析式;
(2)设点C(x,﹣x2+x+2),可求PC=﹣(x﹣2)2+2,由二次函数的性质可求解;
(3)设点P的坐标为(x,﹣x+2),则点C(x,﹣x2+x+2),分三种情况讨论,由平行四边形的性质可出点P的坐标.
解:(1)∵直线y=﹣+2与两坐标轴分别交于A、B两点,
∴当x=0时,y=2,当y=0时,x=4,
∴点A(0,2),点B(4,0)
∵抛物线y=经过点A、B,
∴,
解得:,
∴抛物线解析式为:y=﹣x2+x+2;
(2)设点C(x,﹣x2+x+2),
∵CP∥y轴,
∴点P(x,﹣x+2),
∴PC=yc﹣yp=﹣x2+x+2﹣(﹣x+2)=﹣(x﹣2)2+2,
∵点P在线段AB上运动,
∴0≤x≤4,
∴当x=2时,线段PC的长度的最大值为2;
(3)假设点P的坐标为(x,﹣x+2),
∵PC⊥x轴,
∴点C的横坐标为x,又点C在抛物线上,
∴点C(x,﹣x2+x+2),
①当点P在第一象限内时,假设存在这样的点P,使得四边形AOPC是平行四边形,如图1,
∵四边形OACP是平行四边形,
∴OA=PC=2,
∴2=﹣(x﹣2)2+2,
∴x=2,
∴点P(2,1),
②当点P在第二象限内时,假设存在这样的点P,使得四边形AOCP是平行四边形,如图2,
∵四边形OAPC是平行四边形,
∴OA=PC=2,
∴2=﹣x+2﹣(﹣x2+x+2)
∴x2﹣4x﹣4=0,
∴x=2﹣2或x=2+2(舍去),
∴点P(2﹣2,1+),
③当点P在第四象限内,假设存在这样的点P,使得四边形AOCP是平行四边形,如图3,
∵四边形OAPC是平行四边形,
∴OA=PC=2,
∴2=﹣x+2﹣(﹣x2+x+2)
∴x2﹣4x﹣4=0,
∴x=2﹣2(舍去)或x=2+2,
∴点P(2+2,1﹣),
综上所述:使得以O、A、P、C为顶点的四边形是平行四边形,满足的点P的坐标为:(2,1)或(2+2,1﹣)或(2﹣2,1+).
点评:本题是二次函数综合题,考查了待定系数法求函数解析式,最值问题,平行四边形的性质等知识,解题的关键是灵活运用所学知识解决问题,学会利用分类讨论的思想解决问题.
10.分析:(1)先确定出点B坐标,最后用待定系数法即可得出结论;
(2)先判断出点N是直线BC与对称轴的交点,即可得出结论;
(3)先求出点E坐标,最后用三角形面积公式计算即可得出结论;
(4)设出点P坐标,分三种情况利用用平行四边形的两条对角线互相平分和中点坐标公式求解即可得出结论.
解:(1)针对于直线y=﹣x+4,
令y=0,则0=﹣x+4,
∴x=5,
∴B(5,0),
∵M(3,﹣4)是抛物线的顶点,
∴设抛物线的解析式为y=a(x﹣3)2﹣4,
∵点B(5,0)在抛物线上,
∴a(5﹣3)2﹣4=0,
∴a=1,
∴抛物线的解析式为y=(x﹣3)2﹣4=x2﹣6x+5;
(2)由(1)知,抛物线的解析式为y=(x﹣3)2﹣4,
∴抛物线的对称轴为x=3,
∵点A,B关于抛物线对称轴对称,
∴直线y=﹣x+4与对称轴x=3的交点就是满足条件的点N,
∴当x=3时,y=﹣×3+4=,
∴N(3,)
∵点C是抛物线y=x2﹣6x+5与y轴的交点,
∴C(0,5),
∵点E与点C关于对称轴x=3对称,
∴E(6,5),
由(2)知,N(3,),
∵M(3,﹣4),
∴MN=﹣(﹣4)=,
∴S△EMN=MN?|xE﹣xM|=××3=;
(4)设P(m,n),
∵A(1,0),B(5,0),N(3,),
当AB为对角线时,AB与NP互相平分,
∴(1+5)=(3+m),(0+0)=(+n),
∴m=3,n=﹣,
∴P(3,﹣);
当BN为对角线时,(1+m)=((3+5),(0+n)=(0+),
∴m=7,n=,
∴P(7,);
当AN为对角线时,(1+3)=(5+m),(0+)=(0+n),
∴m=﹣1,n=,
∴P(﹣1,),
即:满足条件的点P的坐标为(3,﹣)或(7,)或(﹣1,).
点评:此题是二次函数综合题,主要考查了待定系数法,三角形面积公式,对称性,平行四边形的性质,用方程的思想解决问题是解本题的关键.
11.分析:(1)抛物线y=ax2+bx﹣3过A(1,0),B(﹣3,0),C(0,﹣3),代入可求出抛物线的解析式,点D在抛物线上且横坐标为﹣2,可求点D的坐标,根据A、D两点坐标,用待定系数法可求直线AD的解析式;
(2)点P在AD上,点Q在抛物线上,当横坐标为m时,相应的纵坐标可以根据解析式表示出来,而PQ的长l就是P点、Q点纵坐标的差,于是可以得到l与m的函数关系式,再依据函数的最值,可求m为何值时,PQ最长,PQ的最大值也能求出;
(3)使P,Q,D,R为顶点的四边形是平行四边形,可以分两种情况:一是PQ为一边时,点R必在直线x=﹣2上,再根据PQ为最大值以下的整数值,得到PQ的整数值,在直线x=﹣2上可以找到点R的位置,确定点R的坐标,得出在点D上方存在,在点D下方也存在;二是PQ为一条对角线时,根据平行四边形的性质,PQ与DR互相平分,此时R与C 重合.
解:(1)设抛物线的解析式为y=ax2+bx+c,将A(1,0),B(﹣3,0)C(0,﹣3)代入y=ax2+bx+c得:
,
解得:,
∴抛物线的解析式为:y=x2+2x﹣3,
当x=﹣2时,y=(﹣2)2﹣4﹣3=﹣3,
∴D(﹣2,﹣3),
设直线AD的解析式为y=kx+b,将A(1,0),D(﹣2,﹣3)代入得:
解得:,
∴直线AD的解析式为y=x﹣1;
因此直线AD的解析式为y=x﹣1,抛物线的解析式为:y=x2+2x﹣3.
(2)∵点P在直线AD上,Q抛物线上,P(m,n),
∴n=m﹣1 Q(m,m2+2m﹣3)
∴PQ的长l=(m﹣1)﹣(m2+2m﹣3)=﹣m2﹣m+2 (﹣2≤m≤1)
∴当m=﹣=时,PQ的长l最大=﹣(﹣)2﹣(﹣)+2=.
答:线段PQ的长度l与m的关系式为:l=﹣m2﹣m+2 (﹣2≤m≤1)
当m=﹣时,PQ最长,最大值为.
(3)①若PQ为平行四边形的一边,则R一定在直线x=﹣2上,如图:
∵PQ的长为0<PQ≤的整数,
∴PQ=1或PQ=2,
当PQ=1时,则DR=1,此时,在点D上方有R1(﹣2,﹣2),在点D下方有R2(﹣2,﹣4);
当PQ=2时,则DR=2,此时,在点D上方有R3(﹣2,﹣1),在点D下方有R4(﹣2,﹣5);
②若PQ为平行四边形的一条对角线,则PQ与DR互相平分,
当PQ=1时,即:x﹣1﹣(x2+2x﹣3)=1,此时x不是整数,
当PQ=2时,即x﹣1﹣(x2+2x﹣3)=2,此时x1=﹣1,x2=0;当x1=﹣1,R与点C重合,即R5(0,﹣3),当x2=0;此时R6(2,﹣1)
综上所述,符合条件的点R有:R1(﹣2,﹣2),R2(﹣2,﹣4),R3(﹣2,﹣1),R4(﹣2,﹣5),R5(0,﹣3),
R6(2,﹣1).
答:符合条件的点R共有6个,即:R1(﹣2,﹣2),R2(﹣2,﹣4),R3(﹣2,﹣1),R4(﹣2,﹣5),R5(0,﹣3)R6(2,﹣1).
点评:本题是二次函数综合题,主要考查了待定系数法求函数的解析式,二次函数的性质,平行四边形的性质等知识,应用分类讨论思想和数形结合思想是解题的关键.
12.分析 :(1)由待定系数法可求抛物线解析式,即可求点B坐标;
(2)分三种情况讨论,由等腰三角形的性质可求解;
(3)由平行四边形的性质可求解.
解:(1)∵抛物线y=x2+bx+c经过点A(2,﹣3)与C(0,﹣3)
∴,
解得,
∴抛物线解析式为:y=x2﹣2x﹣3,
当y=0时,解得x1=3,x2=﹣1
∵点B在x轴负方向,
∴点B坐标为(﹣1,0);
(2)作AM⊥x轴于M,
∴点M(2,0),AM=3,
∴AM=BM=3,
∴∠ABM=45°
∴AB=
当BA=BD时,若点D在B点左侧,此时点D,
若点D在B点右侧,此时点D,
当AD=BD时,显然点D即为点M,坐标(2,0),
当AB=AD时,DM=BM=3,此时点D(5,0),
综上所述:点D坐标为,,(2,0),(5,0);
(3)抛物线解析式为:y=x2﹣2x﹣3,
∴对称轴为x=1,即点N横坐标为1,
∵以A、B、M、N为顶点的四边形是平行四边形,其中AB∥MN,
∴xB﹣xM=xA﹣xN或xB﹣xN=xA﹣xM,
∴﹣1﹣xM=2﹣1或﹣1﹣1=2﹣xM,
∴xM=﹣2或4,
∴M(4,5)或(﹣2,5).
点评:本题是二次函数综合题,考查了待定系数法求解析式,二次函数的性质,等腰三角形的性质,平行四边形的性质,利用分类讨论思想解决问题是本题的关键
与平行四边形相关的压轴题(附答案)
方法提炼:
1、特殊四边形的探究问题解题方法步骤如下:(1)先假设结论成立;(2)设出点坐标,求边长.(类型一方法指导);(3)建立关系式,并计算。若四边形的四个顶点位置已确定,则直接利用四边形边的性质进行计算;若四边形的四个顶点位置不确定,需分情况讨论。
2、 探究平行四边形:①以已知边为平行四边形的某条边,画出所有的符合条件的图形后,利用平行四边形的对边相等进行计算;②以已知边为平行四边形的对角线,画出所有的符合条件的图形后,利用平行四边形对角线互相平分的性质进行计算;③若平行四边形的各顶点位置不确定,需分情况讨论,常以已知的一边作为一边或对角线分情况讨论。
典例引领:
例:如图所示:已知抛物线y=ax2(a≠0)与一次函数y=kx+b的图象相交于两点A(﹣1,﹣1),B(2,﹣4),点P是抛物线上不与A,B重合的一个动点,点Q是y轴上的一个动点.
(1)求a,k,b的值.
(2)直接写出关于x的不等式ax2<kx﹣2的解集;
(3)当点P在直线AB上方时,请求出△PAB面积的最大值并求出此时点P的坐标;
(4)是否存在以P,Q,A,B为顶点的四边形是平行四边形?若存在,请直接写出P,Q的坐标;若不存在,请说明理由.
分析:(1)根据待定系数法得出a,k,b的值;
(2)观察函数图象,即可得出不等式的解集;
(3)过点A作y轴的平行线,过点B作x轴的平行线,两者交于点C,连接PC.根据三角形的面积公式解答即可;
(4)根据平行四边形的性质和坐标特点解答即可.
解:(1)把A(﹣1,﹣1),代入y=ax2中,可得:a=﹣1,
把A(﹣1,﹣1),B(2,﹣4)代入y=kx+b中,可得:,解得,
∴a=﹣1,k=﹣1,b=﹣2;
(2)观察函数图象可知,关于x的不等式ax2<kx﹣2的解集是x<﹣1或x>2;
(3)过点A作y轴的平行线,过点B作x轴的平行线,两者交于点C,
∵A(﹣1,﹣1),B(2,﹣4),
∴C(﹣1,﹣4),AC=BC=3,
设点P的横坐标为m,则点P的纵坐标为﹣m2.
过点P作PD⊥AC于D,作PE⊥BC于E.则D(﹣1,﹣m2),E(m,﹣4),
∴PD=m+1,PE=﹣m2+4.
∴S△APB=S△APC+S△BPC﹣S△ABC,
=×AC?PD+×BC?PE﹣×BC?AC,
=×3×(m+1)×3×(﹣m2+4)﹣×3×3,
=﹣m2+m+3.
∵﹣<0,m=﹣=,
而﹣1<m<2,
∴当m=时,S△APB的最大值为,此时点P的坐标为(,﹣);
(4)存在三组符合条件的点.
当以P,Q,A,B为顶点的四边形是平行四边形时,
∵AP=BQ,AQ=BP,A(﹣1,﹣1),B(2,﹣4),
可得坐标如下:
①P′的横坐标为﹣3,代入二次函数表达式,
解得:P'(﹣3,﹣9),Q'(0,﹣12);
②P″的横坐标为3,代入二次函数表达式,
解得:P″(3,﹣9),Q″(0,﹣6);
③P的横坐标为1,代入二次函数表达式,
解得:P(1,﹣1),Q(0,﹣4).
故:P、Q的坐标分别为(﹣3,﹣9)、(0,﹣12)或(3,﹣9)、(0,﹣6)或(1,﹣1)、(0,﹣4).
点评:主要考查了二次函数的解析式的求法和与几何图形结合的综合能力的培养.要会利用数形结合的思想把代数和几何图形结合起来,利用点的坐标的意义表示线段的长度,从而求出线段之间的关系.
跟踪训练:
1.已知,如图,抛物线y=ax2+bx+c(a≠0)的顶点为M(1,9),经过抛物线上的两点A(﹣3,﹣7)和B(3,m)的直线交抛物线的对称轴于点C.
(1)求抛物线的解析式和直线AB的解析式.
(2)在抛物线上A、M两点之间的部分(不包含A、M两点),是否存在点D,使得S△DAC=2S△DCM?若存在,求出点D的坐标;若不存在,请说明理由.
(3)若点P在抛物线上,点Q在x轴上,当以点A,M,P,Q为顶点的四边形是平行四边形时,直接写出满足条件的点P的坐标.
2.如图①抛物线y=﹣x2+(m﹣1)x+m与直线y=kx+k交于点A、B,其中A点在x轴上,它们与y轴交点分别为C和D,P为抛物线的顶点,且点P纵坐标为4,抛物线的对称轴交直线于点Q.
(1)试用含k的代数式表示点Q、点B的坐标.
(2)连接PC,若四边形CDQP的内部(包括边界和顶点)只有4个横坐标、纵坐标均为整数的点,求k的取值范围.
(3)如图②,四边形CDQP为平行四边形时,
①求k的值;
②E、F为线段DB上的点(含端点),横坐标分别为a,a+n(n为正整数),EG∥y轴交抛物线于点G.问是否存在正整数n,使满足tan∠EGF=的点E有两个?若存在,求出n;若不存在说明理由.
3.如图,在平面直角坐标系中,抛物线y=x2+4x的顶点为点A
(1)求点A的坐标;
(2)点B为抛物线上横坐标等于﹣6的点,点M为线段OB的中点,点P为直线OB下方抛物线上的一动点.当△POM的面积最大时,过点P作PC⊥y轴于点C,若在坐标平面内有一动点Q满足PQ=,求OQ+QC的最小值;
(3)当(2)中OQ+QC取得最小值时,直线OQ与抛物线另一交点为点E,作点E关于抛物线对称轴的对称点E’.点R是抛物线对称轴上的一点,在x轴上是否存在点S,使得以O、E′、R、S为顶点的四边形是平行四边形?若存在,请直接写出S点的坐标;若不存在,请说明理由.
4.综合与探究:
如图,抛物线y=x2﹣x﹣2,与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C抛物线的对称轴为l.
(1)求点A,B,C的坐标;
(2)若点D是第一象限内抛物线上一点,过点D作DE⊥x轴于点E,交直线BC于点F,当OE=4DF时,求四边形DOBF的面积;
(3)在(2)的条件下,若点M在抛物线上,点N在抛物线的对称轴上,是否存在以点B,D,M,N为顶点的四边形是平行四边形?若存在,请求出所有符合条件的点M的坐标;若不存在,请说明理由.
5.如图,在平面直角坐标系中,把抛物线y=x2先向右平移1个单位长度,再向下平移4个单位长度,得到抛物线y=(x﹣h)2+k,所得抛物线与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,顶点为M.
(1)写出h、k的值及点A、B的坐标;
(2)判断△BCM的形状,并计算其面积;
(3)点P是抛物线上的一动点,在y轴上存在点Q,使以点A、B、P、Q为顶点组成的四边形是平行四边形,求点P的坐标.
6.如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(﹣1,0),C(2,3)两点,与y轴交于点N,其顶点为D.
(1)求抛物线及直线AC的函数关系式;
(2)若P是抛物线上位于直线AC上方的一个动点,设点P的横坐标为t;
①当S△ACP=S△ACN时,求点P的坐标;
②是否存在点P,使得△ACP是以AC为斜边的直角三角形?若存在,求点P的坐标;若不存在,请说明理由;
(3)若抛物线的对称轴与直线AC相交于点B,E为直线AC上的任意一点,过点E作EF∥BD交抛物线于点F,以B,D,E,F为顶点的四边形能否为平行四边形?若能,请直接写出点E的坐标;若不能,请说明理由.
7.如图,抛物线y=与x轴分别交于A、B两点(点A在点B的左侧,)与y轴交于点C,作直线AC.
(1)点B的坐标为 ,直线AC的关系式为 .
(2)设在直线AC下方的抛物线上有一动点P,过点P作PD⊥x轴于D,交直线AC于点E,当CE平分∠OEP时求点P的坐标.
(3)点M在x轴上,点N在抛物线上,试问以点A、C、M、N为顶点的四边形能否成为平行四边形?若存在,直接写出所有点M的坐标;若不存在,请简述你的理由.
8.如图,直线y=﹣x+2与x轴交于点A,与y轴交于点B,抛物线y=﹣+bx+c经过A,B两点.
(1)求抛物线的解析式;
(2)点P在抛物线上,点Q在直线AB上,当P,Q关于原点O成中心对称时,求点Q的坐标;
(3)点M为直线AB上的动点,点N为抛物线上的动点,当以点O、B、M、N为顶点的四边形是平行四边形时,请直接写出点M的坐标.
9.如图,已知直线y=﹣x+2与两坐标轴分别交于A、B两点,抛物线y=﹣x2+bx+c经过点A、B,点P为直线AB上的一个动点,过P作y轴的平行线与抛物线交于C点,抛物线与x轴另一个交点为D.
(1)求图中抛物线的解析式;
(2)当点P在线段AB上运动时,求线段PC的长度的最大值;
(3)在直线AB上是否存在点P,使得以O、A、P、C为顶点的四边形是平行四边形?若存在,请求出此时点P的坐标,若不存在,请说明理由.
10.如图,在平面直角坐标系中,抛物线y=ax2+bx+c与两坐标轴分别交于点A、B、C,直线y=﹣x+4经过点B,与y轴交点为D,M(3,﹣4)是抛物线的顶点.
(1)求抛物线的解析式.
(2)已知点N在对称轴上,且AN+DN的值最小.求点N的坐标.
(3)在(2)的条件下,若点E与点C关于对称轴对称,请你画出△EMN并求它的面积.
(4)在(2)的条件下,在坐标平面内是否存在点P,使以A、B、N、P为顶点的四边形是平行四边形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
11.如图,抛物线过A(1,0)、B(﹣3,0),C(0,﹣3)三点,直线AD交抛物线于点D,点D的横坐标为﹣2,点P(m,n)是线段AD上的动点,过点P的直线垂直于x轴,交抛物线于点Q.
(1)求直线AD及抛物线的解析式;
(2)求线段PQ的长度l与m的关系式,m为何值时,PQ最长?
(3)在平面内是否存在整点(横、纵坐标都为整数)R,使得P、Q、D、R为顶点的四边形是平行四边形?若存在,求出点R的坐标;若不存在,说明理由.
12.如图所示,抛物线y=x2+bx+c经过点A(2,﹣3)与C(0,﹣3),与x轴负半轴的交点为B.
(1)求抛物线的解析式与点B坐标;
(2)若点D在x轴上,使△ABD是等腰三角形,求所有满足条件的点D的坐标;
(3)点M在抛物线上,点N在抛物线的对称轴上,若以A、B、M、N为顶点的四边形是平行四边形,其中AB∥MN,请直接写出所有满足条件的点M的坐标.
参考答案
1.分析:(1)二次函数表达式为:y=a(x﹣1)2+9,即可求解;
(2)S△DAC=2S△DCM,则S△DAC=DH(xC﹣xA)=(﹣x2+2x+8﹣2x+1)(1+3)=(9﹣1)(1﹣x)×2,即可求解;
(3)分AM是平行四边形的一条边、AM是平行四边形的对角线两种情况,分别求解即可.
解:(1)二次函数表达式为:y=a(x﹣1)2+9,
将点A的坐标代入上式并解得:a=﹣1,
故抛物线的表达式为:y=﹣x2+2x+8…①,
则点B(3,5),
将点A、B的坐标代入一次函数表达式并解得:
直线AB的表达式为:y=2x﹣1;
(2)存在,理由:
二次函数对称轴为:x=1,则点C(1,1),
过点D作y轴的平行线交AB于点H,
设点D(x,﹣x2+2x+8),点H(x,2x﹣1),
∵S△DAC=2S△DCM,
则S△DAC=DH(xC﹣xA)=(﹣x2+2x+8﹣2x+1)(1+3)=(9﹣1)(1﹣x)×2,
解得:x=﹣1或5(舍去5),
故点D(﹣1,5);
(3)设点Q(m,0)、点P(s,t),t=﹣s2+2s+8,
①当AM是平行四边形的一条边时,
点M向左平移4个单位向下平移16个单位得到A,
同理,点Q(m,0)向左平移4个单位向下平移16个单位为(m﹣4,﹣16),即为点P,
即:m﹣4=s,﹣16=t,而t=﹣s2+2s+8,
解得:s=6或﹣4,
故点P(6,﹣16)或(﹣4,﹣16);
②当AM是平行四边形的对角线时,
由中点公式得:m+s=﹣2,t=2,而t=﹣s2+2s+8,
解得:s=1,
故点P(1,2)或(1﹣,2);
综上,点P(6,﹣16)或(﹣4,﹣16)或(1,2)或(1﹣,2).
点评:本题考查的是二次函数综合运用,涉及到一次函数、平行四边形性质、图形的面积计算等,其中(3),要注意分类求解,避免遗漏.
2.分析:(1)由图可知,抛物线对称轴在y轴右侧,顶点P纵坐标为4,用顶点坐标公式即列得关于m的不等式和方程,求解即得到m的值,进而得到抛物线解析式.把顶点P的横坐标代入直线y=kx+k即得到用k表示点Q的坐标.令抛物线解析式为0,解方程求得点A坐标.把直线与抛物线解析式联立方程组并整理得关于x的一元二次方程,利用韦达定理得xA+xB的值,把xA代入即求得点B横坐标进而求得B的纵坐标.
(2)由(1)得C(0,3),P(1,4),即四边形CDQP的内部(包括边界和顶点)有2个满足横坐标、纵坐标均为整数的点P、C,另外两个满足的点应该是M(0,2)、N(1,3),由图象可知此时点D在线段MS上(不与S(0,1)重合),点Q在线段NR上(不与点R(1,2)重合).因为D(0,k),Q(1,2k),即列得关于k的不等式组,求解即得到k的取值范围.
(3)①求直线CP解析式,由四边形CDQP为平行四边形可得DQ∥CP,即直线y=kx+k的k与直线CP解析式的一次项系数相等,求得k=1.
②过点F作FH⊥⊥EG于点H,则Rt△FGH中,tan∠EGF=,即GH=2FH.由点E、F横坐标分别为a,a+n,可用含a、n的式子表示FH、GH的长,代入GH=2FH,得到关于a的一元二次方程(n为常数).因为满足tan∠EGF=的点E有两个,即关于a的方程有两个不相等的实数根,由△>0求得n的取值范围小于0,故不存在满足条件的正整数n.
解:(1)∵抛物线y=﹣x2+(m﹣1)x+m的顶点P纵坐标为4
∴=4
解得:m1=3,m2=﹣5
∵抛物线对称轴在y轴右侧
∴﹣>0
解得:m>1
∴m=3
∴抛物线为y=﹣x2+2x+3,顶点P(1,4)
∵直线y=kx+k与对称轴交于点Q
∴Q(1,2k)
∵y=﹣x2+2x+3=0时,解得:x1=﹣1,x2=3
∴A(﹣1,0)
∵ 整理得:x2+(k﹣2)x+k﹣3=0
∴xA+xB=﹣(k﹣2)
∴xB=﹣(k﹣2)﹣xA=﹣(k﹣2)﹣(﹣1)=﹣k+3
∴yB=k?xB+k=﹣k2+4k
∴B(﹣k+3,﹣k2+4k)
(2)∵C(0,3),P(1,4),D(0,k),Q(1,2k)
∴当四边形CDQP的内部(包括边界和顶点)只有4个横坐标、纵坐标均为整数的点时,
4个点是C、P、M(0,2)、N(1,3)(如图1)
∴点D在线段MS上(不与S(0,1)重合),点Q在线段NR上(不与点R(1,2)重合)
∴
解得:1<k≤
(3)①∵C(0,3),P(1,4)
∴直线CP解析式为y=x+3
∵四边形CDQP为平行四边形
∴DQ∥CP,即直线y=kx+k平行直线CP
∴k=1
②不存在满足条件的正整数n.
如图2,过点F作FH⊥EG于点H
∴∠FHE=∠FHG=90°
∵k=1
∴直线AB:y=x+1
∵点E在线段DB上横坐标为a,EG∥y轴交抛物线于点G
∴E(a,a+1),G(a,﹣a2+2a+3)
∵点F在线段DB上横坐标为a+n
∴FH=xF﹣xE=n,F(a+n,a+n+1)
∴GH=yG﹣yF=﹣a2+2a+3﹣(a+n+1)=﹣a2+a+2﹣n
∵Rt△FGH中,tan∠EGF=
∴GH=2FH
∴﹣a2+a+2﹣n=2n,整理得:a2﹣a+3n﹣2=0
∵满足tan∠EGF=的点E有两个,
∴关于a的方程a2﹣a+3n﹣2=0有两个不相等的实数根
∴△=1﹣4(3n﹣2)>0
解得:0<n<
∴不存在正整数n,使满足tan∠EGF=的点E有两个
点评:本题考查了二次函数的图象与性质,一元二次方程的解法及根与系数的关系,一元一次不等式的解法,一次函数的图象与性质,三角函数的应用.第(2)题的解题关键是先确定满足条件的4个点中包含C、P,把另外两个横、纵坐标均为整数的点确定下来,再根据直线的位置确定k的取值范围.
3.分析:(1)配方法将抛物线解析式化为顶点式即可;
(2)待定系数法求直线AB解析式为y=﹣2x,设P(m,m2+4m),则H(m,﹣2m),PH=﹣2m﹣(m2+4m)=﹣m2﹣6m,由△PGH∽△MDO可得 PG?MO=PH?MD=3(﹣m2﹣6m)=﹣3m2﹣18m,从而得:S△POM=PG?MO=﹣9m=﹣(m+3)2+,求得P(﹣3,﹣3),在PC上取点T,使得PT=,连接QT,OT,由△QPT∽△CPQ可得TQ=QC,进而可求得OQ+QC的最小值为;
(3)先根据OQ+QC取得最小值时,点O、Q、T三点共线,求得T(,﹣3),待定系数法求得直线OQ解析式为y=x,解方程组可求得点E的坐标,进而可求得E′的坐标,根据以O、E′、R、S为顶点的四边形是平行四边形,分三种情形:①OR为对角线,②OS为对角线,③OE′为对角线,分别求出对应的点S坐标即可.
解:(1)∵y=x2+4x=(x+2)2﹣4,
∴A(﹣2,﹣4);
(2)如图1,过P作PH⊥x轴交OB于H,作PG⊥BC于G,过M作MD⊥y轴交y轴于D,
∵点B为抛物线上横坐标等于﹣6的点,∴B(﹣6,12),
∴直线AB解析式为y=﹣2x
设P(m,m2+4m),则H(m,﹣2m),PH=﹣2m﹣(m2+4m)=﹣m2﹣6m
∵点M为线段OB的中点,∴M(﹣3,6),∴MD=3
∵PH∥y轴
∴∠PHG=∠MOD
∵PG⊥BC MD⊥y轴
∴∠PGH=∠MDO
∴△PGH∽△MDO
∴=,即 PG?MO=PH?MD=3(﹣m2﹣6m)=﹣3m2﹣18m,
∴S△POM=PG?MO=﹣9m=﹣(m+3)2+
∵﹣<0,∴当m=﹣3时,S△POM的值最大,此时P(﹣3,﹣3),
在PC上取点T,使得PT=,连接QT,OT,
∵PC=3,PQ=
∴==
∵∠QPT=∠CPQ
∴△QPT∽△CPQ
∴==,即TQ=QC,
∴OQ+QC=OQ+TQ≥OT
∵OT===
∴OQ+QC的最小值为;
(3)∵当(2)中OQ+QC取得最小值时,点O、Q、T三点共线,T(,﹣3)
∴直线OQ解析式为y=x,
解方程组得,
∴E(,),∵抛物线对称轴为直线x=﹣2,
∴E′(﹣,),
以O、E′、R、S为顶点的四边形是平行四边形,分以下三种情形:
①OR为对角线,∵OE′RS是平行四边形
∴OS∥E′R,OS=E′R=,∴S1 (,0)
②OS为对角线,∵OE′RS是平行四边形
∴OE′∥RS,R(﹣2,),∴S2(,0)
③OE′为对角线,∵OE′RS是平行四边形
∴OS∥E′R,OS=E′R=,∴S3(,0),
综上所述,点S的坐标为:S1 (,0),S2(,0),S3(,0).
点评:本题考查二次函数性质,用待定系数法求一次函数的解析式,图形的平移和对称,一元二次方程的解法,相似三角形的判定和性质,分类讨论思想.第(2)问关键是通过相似三角形转化为两点之间距离最短的问题,第(3)问的关键是分类讨论.
4.分析:(1)把x=0代入抛物线解析式求得y即得到点C坐标;令y=0解方程即求得点A、B坐标.
(2)设点D横坐标为d,用d表示OE、DE的长;求直线BC解析式,用d表示点F坐标,进而用d表示DF的长.根据OE=4DF列方程,求解得点D坐标,即得到各线段的长.由图可知,四边形DOBF面积等于△AED与△BEF面积之差,直接计算即可.
(3)先求出对称轴为直线x=1.以BD为平行四边形的边或对角线进行分类:若BD为边,画出相应的图形,根据平移性质得到点M的横坐标,代入解析式求纵坐标;以BD为对角线,BD与MN互相平分,则BD中点与MN中点相同,利用中点坐标公式列方程即求出点M坐标.
解:(1)当y=x2﹣x﹣2=0时,
解得:x1=﹣2,x2=4
∴A(﹣2,0),B(4,0)
当x=0时,y=x2﹣x﹣2=﹣2
∴C(0,﹣2)
(2)∵点D是第一象限内抛物线上的点
∴设点D坐标为(d,d2﹣d﹣2)(d>4)
∵DE⊥x轴于点E
∴OE=d,DE=d2﹣d﹣2
设直线BC解析式为y=kx﹣2
把点B代入得:4k﹣2=0,解得:k=
∴直线BC:y=x﹣2
∵DE交BC于点F
∴F(d,d﹣2)
∴DF=d2﹣d﹣2﹣(d﹣2)=d2﹣d
∵OE=4DF
∴d=4(d2﹣d)
解得:d1=0(舍去),d2=5
∴D(5,),F(5,)
∴DE=,EF=,BE=OE﹣OB=5﹣4=1
∴S四边形DOBF=S△AED﹣S△BEF=AE?DE﹣BE?EF=×5×﹣×1×=
(3)存在以点B,D,M,N为顶点的四边形是平行四边形
∵A(﹣2,0),B(4,0)
∴对称轴为直线:x==1
∴xN=1
①如图1,BD∥MN,四边形BMND是平行四边形
∴DN∥BM,DN=BM
∴DN向下平移个单位,向左平移1个单位可得BM
∴xM=xN﹣1=0
∴M(0,﹣2)
②如图2,BD∥MN,四边形BDMN是平行四边形
∴DM∥BN,DM=BN
∴BN向上平移个单位,向右平移1个单位可得DM
∴xM=xN+1=2
∴M(2,﹣2)
③以BD为对角线时,BD与MN互相平分
∴BD中点与MN中点相同
∴
设M(m,m2﹣m﹣2),N(1,n)
∴ 解得:
∴M(8,10)
综上所述,符合条件的点M的坐标为(0,﹣2)或(2,﹣2)或(8,10).
点评:本题考查了二次函数的图象与性质,一元二次方程的解法,平行四边形的性质,平移的性质.平行四边形存在性问题中,已知两个顶点时,以此线段为平行四边形的边或对角线进行分类讨论画图并计算;其中固定线段为边长求另外两点时,可利用平移性质求点坐标之间的关系.
5.分析:解:(1)抛物线y=x2先向右平移1个单位长度,再向下平移4个单位长度,得到抛物线y=(x﹣1)2﹣4,
故h=1,k=﹣4,
y=(x﹣1)2﹣4=x2﹣2x﹣3,令y=0,则x=3或﹣1,
即点A、B的坐标分别为(﹣1,0)、(3,0);
(2)点M的坐标为(1,﹣4),
则BC=3,CM=,BM=,
故MB2=BC2+CM2,
故为直角三角形,其面积等于×CM×BC=3=3;
(3)①当AB是平行四边形的一条边时,
即PQ=AB=4,即x=±4,
把x=±4代入函数表达式得:y=5或21,
故点P(4,5)或(﹣4,21);
②当AB是平行四边形的对角线时,
设点P的横坐标为m,点Q的坐标为(0,n),
则AB的中点即为PQ的中点,则m+0=3﹣1,
解得:m=2,故点P(2,﹣3);
综上,点P的坐标为P(4,5)或(﹣4,21)或(2,﹣3).
解:(1)抛物线y=x2先向右平移1个单位长度,再向下平移4个单位长度,得到抛物线y=(x﹣1)2﹣4,
故h=1,k=﹣4,
y=(x﹣1)2﹣4=x2﹣2x﹣3,令y=0,则x=3或﹣1,
即点A、B的坐标分别为(﹣1,0)、(3,0);
(2)点M的坐标为(1,﹣4),
则BC=3,CM=,BM=,
故MB2=BC2+CM2,
故为直角三角形,其面积等于×CM×BC=3=3;
(3)①当AB是平行四边形的一条边时,
即PQ=AB=4,即x=±4,
把x=±4代入函数表达式得:y=5或21,
故点P(4,5)或(﹣4,21);
②当AB是平行四边形的对角线时,
设点P的横坐标为m,点Q的坐标为(0,n),
则AB的中点即为PQ的中点,则m+0=3﹣1,
解得:m=2,故点P(2,﹣3);
综上,点P的坐标为P(4,5)或(﹣4,21)或(2,﹣3).
点评:本题考查的是二次函数综合运用,涉及到平行四边形的性质、点的平移、中点的性质、面积的计算等,其中(3),要注意分类求解,避免遗漏.
6.分析:(1)运用待定系数法即可解决;
(2)①依题意得P(t,﹣t2+2t+3),过点P作PH⊥y轴于H,连接PN,由S△ACP=S△ACN可知PN∥AC,可得PH=HN,建立方程求解即可;②由△ACP是以AC为斜边的直角三角形,可得∠APC=90°,过P作PS⊥x轴于S,过C作CK⊥PS于K,可证△APS∽△PCK,根据相似三角形性质建立方程求解即可;
(3)运用配方法求顶点D坐标,由以B,D,E,F为顶点的四边形能为平行四边形,且EF∥BD,可得EF=BD,设点E(m,m+1),则F(m,﹣m2+2m+3),EF=,建立方程求解即可求得符合题意的点E坐标.
解:(1)将A(﹣1,0),C(2,3)代入y=﹣x2+bx+c中,得
,
解得
∴抛物线解析式为y=﹣x2+2x+3,
设直线AC解析式为y=mx+n,则
,
解得,
∴直线AC解析式为y=x+1;
(2)①在y=﹣x2+2x+3中,令x=0,得y=3,
∴N(0,3),
∵点P的横坐标为t;
∴P(t,﹣t2+2t+3),
过点P作PH⊥y轴于H,连接PN,设直线AC交y轴于G,则G(0,1),∠PHN=90°
∴OA=OG=1,PH=t,HN=OH﹣ON=﹣t2+2t,
∴∠AGO=∠CGN=45°
∵S△ACP=S△ACN
∴PN∥AC
∴∠PNH=∠CGN=45°
∴PH=HN
∴t=﹣t2+2t,解得:t1=0(舍去),t2=1,
∴P(1,4);
②如图2,过P作PS⊥x轴于S,过C作CK⊥PS于K,则∠CKP=∠PSA=90°
∵P(t,﹣t2+2t+3),A(﹣1,0),C(2,3),
∴CK=2﹣t,PK=﹣t2+2t,PS=﹣t2+2t+3,AS=t﹣(﹣1)=t+1,
∵△ACP是以AC为斜边的直角三角形
∴∠APS+∠CPK=∠APC=90°
∵∠PCK+∠CPK=90°
∴∠APS=∠PCK
∴△APS∽△PCK
∴=,即=
解得:t=
∵P是抛物线上位于直线AC上方的一个动点,
∴﹣1<t<2,但>2
∴t=
∴P(,).
(3)∵y=﹣x2+2x+3=﹣(x﹣1)2+4
∴顶点D(1,4)
∴B(1,2),BD=2,
以B,D,E,F为顶点的四边形能为平行四边形.
设点E(m,m+1),则F(m,﹣m2+2m+3),EF=,
∵EF∥BD
∴EF=BD
∴=2,解得:m1=0,m2=1(舍去),m3=,m4=;
∴点E的坐标为:(0,1)或(,)或(,).
点评:本题属于中考压轴题,与二次函数有关的代数几何综合题,涉及知识点多,综合性较强,难度较大,解题时必须熟练掌握并灵活运用相关性质和定理,还要注意数形结合,分类讨论;此题主要考查了二次函数图象和性质,待定系数法求函数解析式,三角形面积,直角三角形性质,平行四边形性质等.
7.分析:(1)y=,令y=0,则x=2或﹣8,令x=0,则y=﹣4,即可求解;
(2)证明△OEC为等腰三角形,OH2+HC2=OC2,即x2+4x2=16,解得:x=,EF=ECsinα=2××,故m=﹣,即可求解;
(3)①当AC是平行四边形的边时,则点A向右平移8个单位向下平移4个单位得到C,即可求解;②当AC是平行四边形的对角线时,利用中点公式即可求解.
解:(1)y=,令y=0,则x=2或﹣8,令x=0,则y=﹣4,
故点A、B、C的坐标分别为:(﹣8,0)、(2,0)、(0,﹣4),
将点A、C的坐标代入一次函数表达式:y=kx+b得:,解得:,
故直线AC的表达式为:y=﹣x﹣4,
故答案为:(2,0),y=﹣x﹣4;
(2)如图,左侧图是局部放大图,
∵CE平分∠OEP时,∴∠OEC=∠CEP,
∵PD∥y轴,∴∠CEP=∠ECO=∠OEC=α,
则△OEC为等腰三角形,
tan∠ECO==2=tanα,则sinα=,
过点E作y轴的垂线交于点F,过点O作OH⊥EC于点H,
设:OH=2x,则CH=x,而OH2+HC2=OC2,即x2+4x2=16,解得:x=,
EF=ECsinα=2××,故m=﹣,
则点P(﹣,﹣);
(3)设:点N(m,n),n=m2+m﹣4,点M(s,0),
①当AC是平行四边形的边时,
则点A向右平移8个单位向下平移4个单位得到C,
同理N(M)向右平移8个单位向下平移4个单位得到M(N),
即m+8=s,n﹣4=0或m﹣8=s,n+4=0,而n=m2+m﹣4,
解得:s=5±或﹣14,
②当AC是平行四边形的对角线时,
利用中点公式得:﹣8=m+s,﹣4=n,而n=m2+m﹣4,
解得:s=﹣2;
故点M的坐标为:(5+,0)或(5﹣)或(﹣14,0)或(﹣2,0).
点评:本题考查的是二次函数综合运用,涉及到平行四边形的性质、图形的平移、解直角三角形等,其中(3),要注意分类求解,避免遗漏.
8.分析:(1)先确定出点A,B坐标,再用待定系数法求出抛物线解析式;
(2)设点Q的作标为(x,y),则P点坐标是(﹣x,﹣y).利用直线方程与抛物线方程联立方程组,求得交点坐标即可;
(3)分OB为边和为对角线两种情况进行求解:①当OB为平行四边形的边时,用MN∥OB,表示和用MN=OB,建立方程求解;
②当OB为对角线时,OB与MN互相平分,交点为H,设出M,N坐标用OH=BH,MH=NH,建立方程组求解即可.
解:(1)∵与x轴交于点A,与y轴交于点B,
∴A(4,0),B(0,2).
∵抛物线经过点A,B,
∴,
∴,
∴抛物线的解析式为;
(2)设点Q的作标为(x,y),则P点坐标是(﹣x,﹣y),
∴,
解得:,;
∴.
(3))①当OB为平行四边形的边时,MN=OB=2,MN∥OB,
∵点M在直线AB上,点N为抛物线上,
∴设M(m,﹣m+2),
∴N(m,﹣m2+m+2),
∴MN=|﹣m2+m+2﹣(﹣m+2)|=|﹣m2+2m|=2,
Ⅰ、﹣m2+2m=2,
解得,m=2,
∴M(2,1),
Ⅱ、﹣m2+2m=2,
解得,m=2,
∴M(2﹣2),M(2+2,1﹣),
②当OB为对角线时,OB与MN互相平分,交点为H,
∴OH=BH,MH=NH,
∵B(0,2),O(0,0),
∴H(0,1),
设M(n,﹣),N(d,),
∴,
解得或,
∴M(﹣2+2,3﹣),M(﹣2﹣2,3+),
即:满足条件的点M的坐标为(2,1)或(2﹣2,1+)或(2+2,1﹣)或(﹣2+2,3﹣)或(﹣2﹣2,3+).
点评:此题是二次函数综合题,主要考查了待定系数法,平行四边形的性质,对称性,解本题的关键是求抛物线解析式,确定点M的坐标时,分类讨论是解本题的难点.
9.分析:(1)把x=0,y=0分别代入解析式可求点A,点B坐标,由待定系数法可求解析式;
(2)设点C(x,﹣x2+x+2),可求PC=﹣(x﹣2)2+2,由二次函数的性质可求解;
(3)设点P的坐标为(x,﹣x+2),则点C(x,﹣x2+x+2),分三种情况讨论,由平行四边形的性质可出点P的坐标.
解:(1)∵直线y=﹣+2与两坐标轴分别交于A、B两点,
∴当x=0时,y=2,当y=0时,x=4,
∴点A(0,2),点B(4,0)
∵抛物线y=经过点A、B,
∴,
解得:,
∴抛物线解析式为:y=﹣x2+x+2;
(2)设点C(x,﹣x2+x+2),
∵CP∥y轴,
∴点P(x,﹣x+2),
∴PC=yc﹣yp=﹣x2+x+2﹣(﹣x+2)=﹣(x﹣2)2+2,
∵点P在线段AB上运动,
∴0≤x≤4,
∴当x=2时,线段PC的长度的最大值为2;
(3)假设点P的坐标为(x,﹣x+2),
∵PC⊥x轴,
∴点C的横坐标为x,又点C在抛物线上,
∴点C(x,﹣x2+x+2),
①当点P在第一象限内时,假设存在这样的点P,使得四边形AOPC是平行四边形,如图1,
∵四边形OACP是平行四边形,
∴OA=PC=2,
∴2=﹣(x﹣2)2+2,
∴x=2,
∴点P(2,1),
②当点P在第二象限内时,假设存在这样的点P,使得四边形AOCP是平行四边形,如图2,
∵四边形OAPC是平行四边形,
∴OA=PC=2,
∴2=﹣x+2﹣(﹣x2+x+2)
∴x2﹣4x﹣4=0,
∴x=2﹣2或x=2+2(舍去),
∴点P(2﹣2,1+),
③当点P在第四象限内,假设存在这样的点P,使得四边形AOCP是平行四边形,如图3,
∵四边形OAPC是平行四边形,
∴OA=PC=2,
∴2=﹣x+2﹣(﹣x2+x+2)
∴x2﹣4x﹣4=0,
∴x=2﹣2(舍去)或x=2+2,
∴点P(2+2,1﹣),
综上所述:使得以O、A、P、C为顶点的四边形是平行四边形,满足的点P的坐标为:(2,1)或(2+2,1﹣)或(2﹣2,1+).
点评:本题是二次函数综合题,考查了待定系数法求函数解析式,最值问题,平行四边形的性质等知识,解题的关键是灵活运用所学知识解决问题,学会利用分类讨论的思想解决问题.
10.分析:(1)先确定出点B坐标,最后用待定系数法即可得出结论;
(2)先判断出点N是直线BC与对称轴的交点,即可得出结论;
(3)先求出点E坐标,最后用三角形面积公式计算即可得出结论;
(4)设出点P坐标,分三种情况利用用平行四边形的两条对角线互相平分和中点坐标公式求解即可得出结论.
解:(1)针对于直线y=﹣x+4,
令y=0,则0=﹣x+4,
∴x=5,
∴B(5,0),
∵M(3,﹣4)是抛物线的顶点,
∴设抛物线的解析式为y=a(x﹣3)2﹣4,
∵点B(5,0)在抛物线上,
∴a(5﹣3)2﹣4=0,
∴a=1,
∴抛物线的解析式为y=(x﹣3)2﹣4=x2﹣6x+5;
(2)由(1)知,抛物线的解析式为y=(x﹣3)2﹣4,
∴抛物线的对称轴为x=3,
∵点A,B关于抛物线对称轴对称,
∴直线y=﹣x+4与对称轴x=3的交点就是满足条件的点N,
∴当x=3时,y=﹣×3+4=,
∴N(3,)
∵点C是抛物线y=x2﹣6x+5与y轴的交点,
∴C(0,5),
∵点E与点C关于对称轴x=3对称,
∴E(6,5),
由(2)知,N(3,),
∵M(3,﹣4),
∴MN=﹣(﹣4)=,
∴S△EMN=MN?|xE﹣xM|=××3=;
(4)设P(m,n),
∵A(1,0),B(5,0),N(3,),
当AB为对角线时,AB与NP互相平分,
∴(1+5)=(3+m),(0+0)=(+n),
∴m=3,n=﹣,
∴P(3,﹣);
当BN为对角线时,(1+m)=((3+5),(0+n)=(0+),
∴m=7,n=,
∴P(7,);
当AN为对角线时,(1+3)=(5+m),(0+)=(0+n),
∴m=﹣1,n=,
∴P(﹣1,),
即:满足条件的点P的坐标为(3,﹣)或(7,)或(﹣1,).
点评:此题是二次函数综合题,主要考查了待定系数法,三角形面积公式,对称性,平行四边形的性质,用方程的思想解决问题是解本题的关键.
11.分析:(1)抛物线y=ax2+bx﹣3过A(1,0),B(﹣3,0),C(0,﹣3),代入可求出抛物线的解析式,点D在抛物线上且横坐标为﹣2,可求点D的坐标,根据A、D两点坐标,用待定系数法可求直线AD的解析式;
(2)点P在AD上,点Q在抛物线上,当横坐标为m时,相应的纵坐标可以根据解析式表示出来,而PQ的长l就是P点、Q点纵坐标的差,于是可以得到l与m的函数关系式,再依据函数的最值,可求m为何值时,PQ最长,PQ的最大值也能求出;
(3)使P,Q,D,R为顶点的四边形是平行四边形,可以分两种情况:一是PQ为一边时,点R必在直线x=﹣2上,再根据PQ为最大值以下的整数值,得到PQ的整数值,在直线x=﹣2上可以找到点R的位置,确定点R的坐标,得出在点D上方存在,在点D下方也存在;二是PQ为一条对角线时,根据平行四边形的性质,PQ与DR互相平分,此时R与C 重合.
解:(1)设抛物线的解析式为y=ax2+bx+c,将A(1,0),B(﹣3,0)C(0,﹣3)代入y=ax2+bx+c得:
,
解得:,
∴抛物线的解析式为:y=x2+2x﹣3,
当x=﹣2时,y=(﹣2)2﹣4﹣3=﹣3,
∴D(﹣2,﹣3),
设直线AD的解析式为y=kx+b,将A(1,0),D(﹣2,﹣3)代入得:
解得:,
∴直线AD的解析式为y=x﹣1;
因此直线AD的解析式为y=x﹣1,抛物线的解析式为:y=x2+2x﹣3.
(2)∵点P在直线AD上,Q抛物线上,P(m,n),
∴n=m﹣1 Q(m,m2+2m﹣3)
∴PQ的长l=(m﹣1)﹣(m2+2m﹣3)=﹣m2﹣m+2 (﹣2≤m≤1)
∴当m=﹣=时,PQ的长l最大=﹣(﹣)2﹣(﹣)+2=.
答:线段PQ的长度l与m的关系式为:l=﹣m2﹣m+2 (﹣2≤m≤1)
当m=﹣时,PQ最长,最大值为.
(3)①若PQ为平行四边形的一边,则R一定在直线x=﹣2上,如图:
∵PQ的长为0<PQ≤的整数,
∴PQ=1或PQ=2,
当PQ=1时,则DR=1,此时,在点D上方有R1(﹣2,﹣2),在点D下方有R2(﹣2,﹣4);
当PQ=2时,则DR=2,此时,在点D上方有R3(﹣2,﹣1),在点D下方有R4(﹣2,﹣5);
②若PQ为平行四边形的一条对角线,则PQ与DR互相平分,
当PQ=1时,即:x﹣1﹣(x2+2x﹣3)=1,此时x不是整数,
当PQ=2时,即x﹣1﹣(x2+2x﹣3)=2,此时x1=﹣1,x2=0;当x1=﹣1,R与点C重合,即R5(0,﹣3),当x2=0;此时R6(2,﹣1)
综上所述,符合条件的点R有:R1(﹣2,﹣2),R2(﹣2,﹣4),R3(﹣2,﹣1),R4(﹣2,﹣5),R5(0,﹣3),
R6(2,﹣1).
答:符合条件的点R共有6个,即:R1(﹣2,﹣2),R2(﹣2,﹣4),R3(﹣2,﹣1),R4(﹣2,﹣5),R5(0,﹣3)R6(2,﹣1).
点评:本题是二次函数综合题,主要考查了待定系数法求函数的解析式,二次函数的性质,平行四边形的性质等知识,应用分类讨论思想和数形结合思想是解题的关键.
12.分析 :(1)由待定系数法可求抛物线解析式,即可求点B坐标;
(2)分三种情况讨论,由等腰三角形的性质可求解;
(3)由平行四边形的性质可求解.
解:(1)∵抛物线y=x2+bx+c经过点A(2,﹣3)与C(0,﹣3)
∴,
解得,
∴抛物线解析式为:y=x2﹣2x﹣3,
当y=0时,解得x1=3,x2=﹣1
∵点B在x轴负方向,
∴点B坐标为(﹣1,0);
(2)作AM⊥x轴于M,
∴点M(2,0),AM=3,
∴AM=BM=3,
∴∠ABM=45°
∴AB=
当BA=BD时,若点D在B点左侧,此时点D,
若点D在B点右侧,此时点D,
当AD=BD时,显然点D即为点M,坐标(2,0),
当AB=AD时,DM=BM=3,此时点D(5,0),
综上所述:点D坐标为,,(2,0),(5,0);
(3)抛物线解析式为:y=x2﹣2x﹣3,
∴对称轴为x=1,即点N横坐标为1,
∵以A、B、M、N为顶点的四边形是平行四边形,其中AB∥MN,
∴xB﹣xM=xA﹣xN或xB﹣xN=xA﹣xM,
∴﹣1﹣xM=2﹣1或﹣1﹣1=2﹣xM,
∴xM=﹣2或4,
∴M(4,5)或(﹣2,5).
点评:本题是二次函数综合题,考查了待定系数法求解析式,二次函数的性质,等腰三角形的性质,平行四边形的性质,利用分类讨论思想解决问题是本题的关键
同课章节目录
