2021年中考二轮复习数学《探索二次函数综合型压轴题解题技巧》分类训练八:与相似三角形相关的压轴题(word版含答案)
文档属性
| 名称 | 2021年中考二轮复习数学《探索二次函数综合型压轴题解题技巧》分类训练八:与相似三角形相关的压轴题(word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 697.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-20 00:00:00 | ||
图片预览




文档简介
2021中考数学复习《探索二次函数综合型压轴题解题技巧》分类训练八:
与相似三角形相关的压轴题(附答案)
方法提炼:
1、求一点使两个三角形相似的问题,我们可以先找出可能相似的三角形,一般是有几种情况,需要分类讨论,然后根据两个三角形相似的边长相似比来求点的坐标。
典例引领:
例:如图,直线y=-x+3交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c经过A、B、C(1,0)三点。
(1)求抛物线的解析式;?
(2)若点D的坐标为(-1,0),在直线y=-x+3上有一点P,使ΔABO与ΔADP相似,求出点P的坐标;
解:(1)抛物线的解析式为y=x2-4x+3
(2)由题意可得:△ABO为等腰三角形, ? ?
若△ABO∽△AP1D ,则=? ? ??
∴DP1=AD=4??,?∴P1(1,4)
若△ABO∽△ADP2?,过点P2作P2?M⊥x轴于M,AD=4,?
∵△ABO为等腰三角形,?∴△ADP2是等腰三角形,由三线合一可得:DM=AM=2=?P2M,
?即点M与点C重合???,∴P2(1,2)
跟踪训练:
1.如图,在平面直角坐标系xOy中,抛物线与x轴相交于点A(﹣2,0)、B(4,0),与y轴交于点C(0,﹣4),BC与抛物线的对称轴相交于点D.
(1)求该抛物线的表达式,并直接写出点D的坐标;
(2)过点A作AE⊥AC交抛物线于点E,求点E的坐标;
(3)在(2)的条件下,点F在射线AE上,若△ADF∽△ABC,求点F的坐标.
2.如图1,已知二次函数y=ax2﹣a(a为常数,且a≠0)与x轴交于A、B,与y轴的交点为C.过点A的直线l:y=kx+b(k,b为常数,且k≠0)与抛物线另一交点为E,交y轴于D.
(1)用含k的式子表示直线l的解析式;
(2)若a=3,k=,点P为抛物线上第四象限上的一动点,过P作y轴的平行线交AD于M,作PN⊥AD于N,当△PMN面积有最大值时,求点P的坐标;
(3)如图2,若a=3,k=1,连结AC、BC,在坐标平面内,求使得△ACD与△BCQ相似(其中点Q与点A是对应顶点)的Q的坐标.
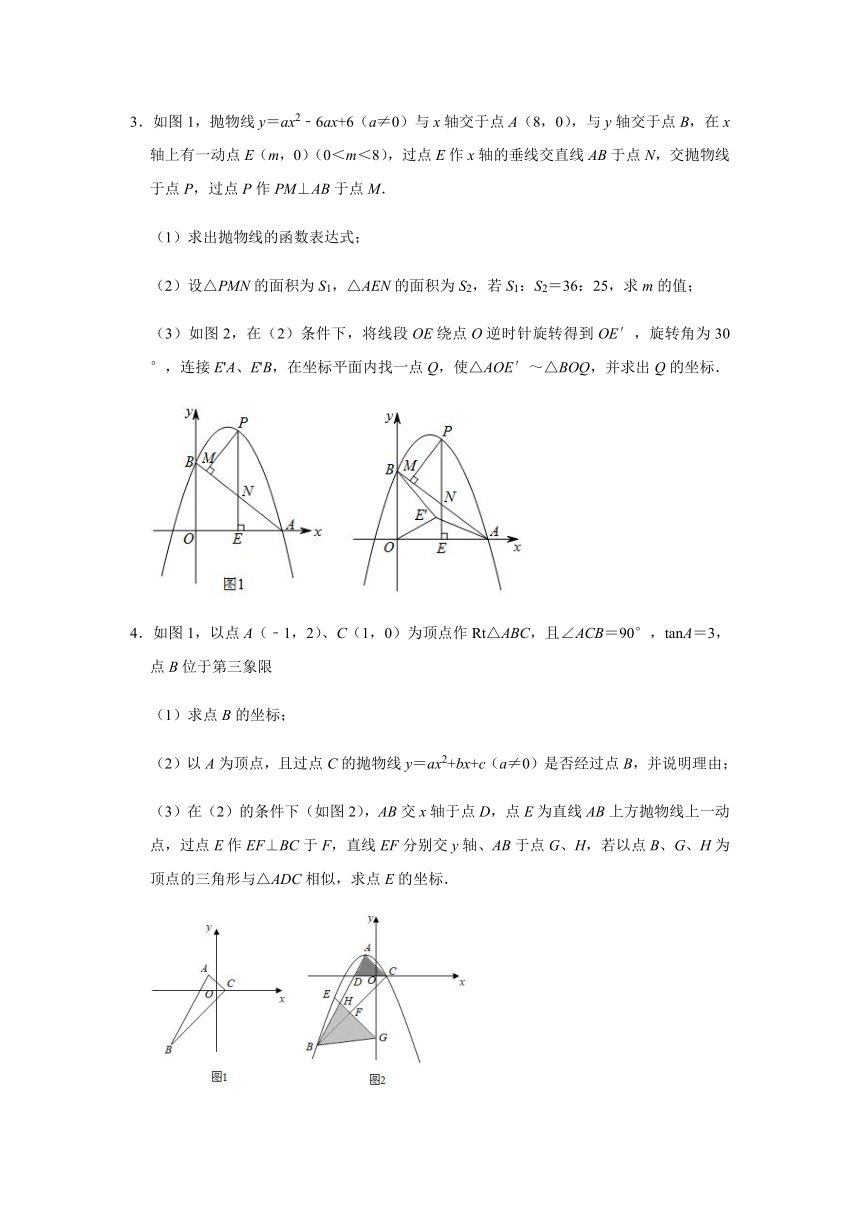
3.如图1,抛物线y=ax2﹣6ax+6(a≠0)与x轴交于点A(8,0),与y轴交于点B,在x轴上有一动点E(m,0)(0<m<8),过点E作x轴的垂线交直线AB于点N,交抛物线于点P,过点P作PM⊥AB于点M.
(1)求出抛物线的函数表达式;
(2)设△PMN的面积为S1,△AEN的面积为S2,若S1:S2=36:25,求m的值;
(3)如图2,在(2)条件下,将线段OE绕点O逆时针旋转得到OE′,旋转角为30°,连接E'A、E'B,在坐标平面内找一点Q,使△AOE′~△BOQ,并求出Q的坐标.
4.如图1,以点A(﹣1,2)、C(1,0)为顶点作Rt△ABC,且∠ACB=90°,tanA=3,点B位于第三象限
(1)求点B的坐标;
(2)以A为顶点,且过点C的抛物线y=ax2+bx+c(a≠0)是否经过点B,并说明理由;
(3)在(2)的条件下(如图2),AB交x轴于点D,点E为直线AB上方抛物线上一动点,过点E作EF⊥BC于F,直线EF分别交y轴、AB于点G、H,若以点B、G、H为顶点的三角形与△ADC相似,求点E的坐标.
5.抛物线C1:y=ax2+bx+3与x轴交于A(﹣3,0)、B两点,与y轴交于点C,点M(﹣2,3)是抛物线上一点.
(1)求抛物线C1的表达式.
(2)若抛物线C2关于C1关于y轴对称,点A、B、M关于y轴的对称分别为A′、B′、M′.过点M′作M′E⊥x轴于点E,交直线A′C于点D,在x轴上是否存在点P,使得以A′、D、P为顶点的三角形与△AB′C相似?若存在,请求出点P的坐标;若不存在,请说明理由.
6.如图,已知抛物线经过点A(﹣1,0),B(2,0),C(0,2),点D为OC中点,连接AC、BD,并延长BD交AC于点E.
(1)求抛物线w1的表达式;
(2)若抛物线w1与抛物线w2关于y轴对称,在抛物线w2位于第二象限的部分上取一点Q,过点Q作QF⊥x轴,垂足为点F,是否存在这样的F点,使得△QFO与△CDE相似?若存在,求出点F的坐标,若不存在,请说明理由.
7.在平面直角坐标系中,如图1,抛物线y=ax2+bx+c的对称轴为x=,与x轴的交点A(﹣1,0)与y轴交于点C(0,﹣2).
(1)求抛物线的解析式;
(2)如图2.点P是直线BC下方抛物线上的一点,过点P作BC的平行线交抛物线于点Q(点Q在点P右侧),连结BQ,当△PCQ的面积为△BCQ面积的一半时,求P点的坐标;
(3)现将该抛物线沿射线AC的方向进行平移,平移后的抛物线与直线AC的交点为A'、C'(点C'在点A'的下方),与x轴的交点为B',当△AB'C'与△AA'B'相似时,求出点A′的横坐标.
8.如图,以D为顶点的抛物线y=﹣x2+bx+c交x轴于A、B两点,交y轴于点C,直线BC的表达式为y=﹣x+3.
(1)求抛物线的表达式.
(2)请你判断△BCD的形状,并说明理由.
(3)在x轴上是否存在一点Q,使得以A、C、Q为顶点的三角形与△BCD相似?若存在,请求出点Q的坐标;若不存在,请说明理由.
9.如图,已知动圆A恒过定点B(0,﹣1),圆心A在抛物线y=﹣x2上运动,MN为⊙A在x轴上截得的弦(点M在点N左侧).
(1)当点A坐标为(,a)时,求a的值,并计算此时⊙A的半径与弦MN的长;
(2)当⊙A的圆心A运动时,判断弦MN的长度是否发生变化?若改变,请举例说明;若不变,请说明理由;
(3)连接BM,BN,当△OBM与△OBN相似时,计算点M的坐标.
10.如图,已知二次函数y=﹣x2+bx+c(b,c为常数)的图象经过点A(3,1),点C(0,4),顶点为点M,过点A作AB∥x轴,交y轴于点D,交该二次函数图象于点B,连结BC.
(1)求该二次函数的解析式及点M的坐标;
(2)若将该二次函数图象向下平移m(m>0)个单位,使平移后得到的二次函数图象的顶点与△ABC的外心重合,求m的取值;
(3)点P是坐标平面内的一点,使得△ACB与△MCP相似,且CM的对应边为AC,请写出所有点P的坐标(直接写出结果,不必写解答过程).
11.如图1,已知抛物线;C1:y=﹣(x+2)(x﹣m)(m>0)与x轴交于点B、C(点B在点C的左侧),与y轴交于点E.
(1)求点B、点C的坐标;
(2)当△BCE的面积为6时,若点G的坐标为(0,b),在抛物线C1的对称轴上是否存在点H,使得△BGH的周长最小,若存在,则求点H的坐标(用含b的式子表示);若不存在,则请说明理由;
(3)在第四象限内,抛物线C1上是否存在点F,使得以点B、C、F为顶点的三角形与△BCE相似?若存在,求m的值;若不存在,请说明理由.
12.如图,抛物线y=(x+2)2+m与x轴交于A,B两点,与y轴交于点C.点D在抛物线上,且与点C关于抛物线的对称轴对称,抛物线的顶点为M,点B的坐标为(﹣1,0).
(1)求抛物线的解析式及A,C,D的坐标;
(2)判断△ABM的形状,并证明你的结论;
(3)若点P是直线BD上一个动点,是否存在以P,C,D为顶点的三角形与△ABD相似?若存在,请直接写出点P的坐标;若不存在,请说明理由
13.已知一次函数y=kx+2的图象经过点,与x轴相交于点A,与y轴相交于点B,二次函数y=ax2+bx(a>0)的图象经过点A和点P,顶点为M,对称轴与一次函数的图象相交于点N.
(1)求一次函数的解析式以及A点,B点的坐标;
(2)求顶点M的坐标;
(3)在y轴上求一点Q,使得△PNM和△PBQ相似.
14.如图,已知抛物线y=ax2+bx﹣3与x轴交于A、B两点,A(﹣1,0)与y轴交于点C,点E(1,﹣4)为抛物线的顶点,且OD=OA.
(1)求抛物线的解析式;
(2)设∠DBC=α,∠CBE=β,求sin(α﹣β)的值;
(3)探究坐标轴上是否存在点P,使得以P、A、C三点为顶点的三角形与△BCE相似,若存在,请指出点P的位置,并直接写出点P的坐标,若不存在,请说明理由.
参考答案
1.解:(1)设抛物线的解析式为y=a(x+2)(x﹣4),将C(0,﹣4)代入得:﹣8a=﹣4,解得:a=,
∴抛物线的解析式为y=x2﹣x﹣4.
如图1所示:记抛物线的对称轴与x轴交点坐标为F.
∵抛物线的对称轴为x=﹣=1,
∴BF=OB﹣OF=3.
∵BO=OC=4,∠BOC=90°,
∴∠OBC=45°.
∴△BFD为等腰直角三角形.
∴FD=FB=3.
∴D(1,﹣3).
(2)如图2,过点E作EH⊥AB,垂足为H.
∵∠EAB+∠BAC=90°,∠BAC+∠ACO=90°,
∴∠EAH=∠ACO.
∴tan∠EAH=tan∠ACO=.
设EH=t,则AH=2t,
∴点E的坐标为(﹣2+2t,t).
将(﹣2+2t,t)代入抛物线的解析式得:(﹣2+2t)2﹣(﹣2+2t)﹣4=t,
解得:t=或t=0(舍去)
∴E(5,).
(3)A、B、C、D四个点坐标分别为:A(﹣2,0),B(4,0),C(0,﹣4),D(1,﹣3),
则:AD=3,AB=6,AC=2,BC=4,
∵△ADF∽△ABC,
∴,
∴,
∴AF=,
设:点F坐标为(x,x+1),
过点F作x轴的垂线交x轴于点H,
则:AF2=FH2+AH2,
即:10=(x+1)2+(x+2)2,
解得:x=﹣2+2或﹣2﹣2(舍去),
故点F坐标为(﹣2+2,).
2.解:(1)∵二次函数y=ax2﹣a(a为常数,且a≠0)与x轴交于A,
∴y=0时,ax2﹣a=0,
解得:x1=1,x2=﹣1,
∴A(﹣1,0),
∵直线l:y=kx+b(k,b为常数,且k≠0)过点A,
∴﹣k+b=0,
∴b=k,
∴直线l的解析式为y=kx+k;
(2)∵a=3,k=,
∴二次函数解析式为y=3x2﹣3,直线l的解析式为y=,
∴D(0,),
∴OA=1,OD=,
∴AD===,
设点P的坐标为(x,3x2﹣3),则点M (x,),
∴PM=,
∵PM∥y轴,
∴∠PMN=∠ADO.
又∵∠PNM=∠AOD=90°,
∴△PMN∽△ADO,
∴,
∴=,
∴当PM有最大值时,S△PMN的面积最大,此时x=,
∴,
∴.
(3)△ACD与△QBC相似,
当a=3,k=1时,二次函数解析式为y=3x2﹣3,直线l的解析式为y=x+1,
∴C(0,﹣3),B(1,0),D(0,1),
∴,CD=4,AC=,BC=,
设点Q坐标为(x,y)
若△ACD∽△QBC,
∴,
∴,
∴,
∴,
解得:,,
∴Q点的坐标为()或;
若△ACD∽△QCB,
∴,
∴,
∴,
∴,
解得:或,
∴Q点的坐标为(0,﹣)或(),
综上所述:点Q坐标为:或或或().
3.解:(1)把A(8,0)代入y=ax2﹣6ax+6,得64a﹣48a+6=0,解得a=,
∴抛物线的函数表达式为:y=x2+x+6;
(2)如图1,在y=x2+x+6中,令x=0,得y=6,
∴B(0,6),
设直线AB解析式为y=kx+b,则,解得
∴直线AB解析式为y=x+6
∵PE⊥x轴,PM⊥AB
∴∠AEN=∠PMN=90°,
∵∠ANE=∠PNM
∴△ANE∽△PNM
∴==,==()2,
∵S1:S2=36:25,
∴=
∴=,即6AN=5PN
∵E(m,0)(0<m<8),
∴P(m,+m+6),N(m,m+6)
∴EN=m+6,PN=PE﹣EN=+m+6﹣(m+6)=+3m
OE=m,AE=8﹣m,
∵AB===10
∴cos∠OAB==,即=
∴AN=(8﹣m),
∴6×(8﹣m)=5×(+3m),解得:m1=4,m2=8(不符合题意,舍去),
∴m=4;
(3)如图2,∵线段OE绕点O逆时针旋转得到OE′,旋转角为30°,
∴OE′=OE=4,∠AOE′=30°
∵△AOE′~△BOQ,
∴=,∠BOQ=∠AOE′=30°,
∴=,即OQ=3,过点Q作QH⊥y轴于H,
∴QH=OQ=,OH===,
∴当点Q在y轴右侧时,Q1(,),
当点Q在y轴左侧时,Q2(﹣,).
综上所述,Q的坐标为:Q1(,),Q2(﹣,).
4.解:(1)过C点作MN垂直x轴.过A、B两点分别作AM⊥MN,垂足为M,BN⊥MN,垂足为N,
∵∠ACB=90°,
∴∠CBN=∠ACM,
∴△CNB~△AMC,
∴,
∵A(﹣1,2)、C(1,0),
∴AM=2,CM=2,
又∵tanA==3,
∴BN=6,CN=6,
∴B点坐标为(﹣5,﹣6).
(2)设以A(﹣1,2)为顶点的抛物线为y=a(x+1)2+2,
∵抛物线经过C(1,0)
∴a(1+1)2+2=0,
∴,
∴函数解析式为,
当x=﹣5时,y==﹣6,
∴以A为顶点,且过点C的抛物线为经过点BB(﹣5,﹣6).
(3)∵点A(﹣1,2)、C(1,0),
∴直线yAC=﹣x+1,∠ACD=45°,
∵EF⊥BC,
∴∠BHC=DAC,
∴以点B、G、H为顶点的三角形与△ADC相似,有两种情况:
Ⅰ.如图2(1).∠HGB=45°,∵EG∥AC,∴BG∥CD,即BG⊥y轴,
∴G坐标为(0,﹣6)
∴直线yEG=﹣x﹣6,
依题意得:,
解得(不合题意舍去),得,
∴当∠HGB=∠ACD=45°时△HBG∽ADC,即:E点坐标为().
Ⅱ.如图2(2).∠HBG=∠ACD=45°时,△HBG∽△ACD,
∵过B点作BP⊥y轴,∴P点(0,﹣6)
∵∠CBP=45°,
∴∠GBP=∠ABC,
又∵tan∠GBP=,tan∠ABC=,BP=5,
∴GP=,即G点坐标为(0,),
∴直线,
依题意得:,
解得,(不合题意舍去),得,
即E点为(,),
综上所述:E点坐标为()或(,),
5.解:(1)将点A、M的坐标代入函数表达式得:,解得:,
故抛物线C1的表达式为:y=﹣x2﹣2x+3;
(2)由题意得:点A(﹣3,0)、B(1,0)、C(0,3)、M(﹣2,3)、B′(﹣1,0)、A′(3,0),D(2,1),
则AB′=2,AC=3,B′C=,A′D=,
①当点P在直线AC的左侧时,
当点P在DM′左侧时,
A′、D、P为顶点的三角形与△AB′C相似,
则△AB′C∽△A′DP,则,
即:,解得:A′P=3,
故点P(0,0),
当点P在DM′左侧时,
同理可得点P(P′)(,0);
②当点P在直线AC的右侧时,
则△AB′C、△DA′P″不相似,
综上,点P的坐标为(0,0)或(,0).
6.解:(1)设抛物线的解析式为y=ax2+bx+c,将A(﹣1,0),B(2,0),C(0,2)代入抛物线的解析式得:
,
解得:,
∴抛物线w1的表达式为y=﹣x2+x+2;
(2)∵抛物线w1与抛物线w2关于y轴对称,
∴抛物线w2的解析式y=﹣x2﹣x+2,
∵点D为OC中点,C(0,2),
∴D(0,1),
∵A(﹣1,0),B(2,0),
∴,
∵∠AOC=∠BOD=90°,
∴△AOC∽△DOB,
∴∠ACO=∠DBO,
∴BD⊥AC,
∴,
设F(a,0),Q(a,﹣a2﹣a+2),a<0,若△QFO与△CDE相似,可分两种情况考虑:
①△QFO与∽△CED时,
,
∴,
解得:a1=﹣1,a2=2(舍去),
∴F(﹣1,0);
②△QFO∽△DEC时,
,
∴,
解得:,(舍去),
∴F(,0).
综合以上可得F点的坐标为F(﹣1,0)或F(,0).
7.解:(1)由对称性可知B(4,0)
设抛物线解析式为y=a(x+1)(x﹣4)
将(0,﹣2)代入得a=
∴y=x2﹣x﹣2.
(2)由平行线间距离处处相等可知,当△PCQ的面积为△BCQ面积的一半时,PQ=BC
∵C(0,﹣2),B(4,0)
∴BC=
∴PQ=
∴PQ2=+=5
∵直线BC的解析式为y=x﹣2,PQ∥BC
∴设直线PQ的解析式为y=x+b
则yP=xP+b,yQ=y=xQ+b
联立得
x2﹣4x﹣4﹣2b=0
则xP+xQ=4
∵PQ2=+=5
∴=5,xQ﹣xP=2
∴点P(1,﹣3)
(3)由点A(﹣1,0),C(0,﹣2)得直线AC的解析式为y=﹣2x﹣2
设点A'坐标为(a,﹣2a﹣2),由平移的性质,可知AC=A'C'=
平移距离为AA'=(a+1)
∴AC'=(a+2)
当△AB'C'与△AA'B'相似时,只有当△AB'C'∽△AA'B'
∴AB'2=AA'×AC'=5(a+1)(a+2)
过点B'作AA'的平行线,交原抛物线于点D,连接AD,
由平移知四边形ADB'A'为平行四边形,点D的纵坐标为2a+2
设点D的横坐标为m,则点B'坐标为(m+a+1,0)
∴AB'2=(m+a+2)2=5(a+1)(a+2),①
将点D(m,2a+2)代入y=x2﹣x﹣2得
﹣﹣2=2a+2,②
联立①②,解得:a=,
m2﹣9m+15=0,
∴m=,或m=(舍)
∴a═==
∴点A′的横坐标为.
8.解:(1)把x=0代入y=﹣x+3,得:y=3,
∴C(0,3)
把y=0代入y=﹣x+3,得:x=3,
∴B(3,0)
将C(0,3)、B(3,0)代入y=﹣x2+bx+c得:,
解得
∴抛物线的解析式为y=﹣x2+2x+3;
(2)△BCD是直角三角形,理由如下:
由y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴D(1,4)
又∵C(0,3)、B(3,0)、D(1,4),
∴CD==,BC==3,DB==2
∵()2+(3)2=20,(2)2=20,
∴CD2+BC2=BD2,
∴∠BCD=90°.即△BCD是直角三角形;
(3)如图,连接AC,把y=0代入y=﹣x2+2x+3,
解得:x=﹣1或x=3,
∴A(﹣1,0),
∴OA=1,
∴=,
∵=,
∴,
又∵∠AOC=DCB=90°,
∴△AOC∽△DCB.
∴当Q的坐标为(0,0)时,△AQC∽△DCB,
过点C作CQ⊥AC,交x轴与点Q.
∵△ACQ为直角三角形,CO⊥AQ,
∴△ACQ∽△AOC.
又∵△AOC∽△DCB,
∴△ACQ∽△DCB,
∴,即,
解得:AQ=10.
∴Q(9,0).
综上所述,当Q的坐标为(0,0)或(9,0)时,以A、C、Q为顶点的三角形与△BCD相似.
9.解:(1)把点A()代入得,
a=﹣,
∵B(0,﹣1),
∴AB∥x轴,
∴⊙A的半径为,
如图1,过点A作AE⊥MN于点E,连接AM,
则AM=AB=,
∴ME===1,
由垂径定理,MN=2ME=2×1=2.
故此时⊙A的半径为,弦MN的长为2;
(2)MN不变.如图2,理由如下:
设点A(m,n),则AB2=m2+(n+1)2,
在Rt△AME中,ME2=AM2﹣AE2=m2+(n+1)2﹣n2=m2+2n+1,
∵点A在抛物线y=﹣x2上,
﹣m2=n,
将n=﹣代入ME2=m2+2n+1得,
ME2=1,
ME=1,
由垂径定理得,MN=2ME=2×1=2(是定值,不变);
(3)由(2)知MN=2,
设M(x,0),则N(x+2,0).
当△OBM与△OBN相似,有以下情况:
①M、N在y轴同侧,
∵△OBM与△OBN相似,
∴,
即OB2=OM?ON,
∴x(x+2)=1,
整理得,x2+2x﹣1=0,
解得:,
∴当M、N在y轴右侧时,M(﹣1+,0),
当M、N在y轴左侧时,M(﹣1﹣,0),
②M、N在y轴两侧时,
∵△OBM与△OBN相似,
∴,
即OB2=OM?ON,
﹣x(x+2)=1,
整理得,x2+2x+1=0,
解得x=﹣1,
此时△OBM与△OBN全等,M(﹣1,0),
综合以上可得,M点的坐标为(﹣1+,0)或(﹣1﹣,0)或(﹣1,0).
10.解:(1)C(0,4),则c=4,抛物线表达式为:y=﹣x2+bx+4,
将点A的坐标代入上式并解得:b=2,
故抛物线的表达式为:y=﹣x2+2x+4,
则点M(1,5);
(2)点A(3,1)函数的对称轴为:x=1,则点B(﹣1,1),点C(0,4),
直线BC的中点坐标为:(﹣,),
则线段BC的中垂线的函数表达式为:y=﹣x+,
当x=1时,y=2,即外心坐标为(1,2),
则二次函数图象向下平移了5﹣2=3个单位;
(3)△ACB与△MCP相似,且CM的对应边为AC,存在△ACB∽△CMP或△CAB∽△CMP,
点A、B、C、M的坐标分别为:(3,1)、(﹣1,1)、(0,4)、(1,5),
则AB=4,BC=,AC=3,CM=,
①当△ACB∽△CMP时,如下图左侧图,
则,即,
解得:PM=,PC=,
设点P(r,s),
则r2+(s﹣4)2=,(r﹣1)2+(s﹣5)2=,
解得:r=,s=4或r=0,s=
故点P(,4)或(0,);
②当△CAB∽△CMP时,如上图右侧图,
则点P在直线CA上,直线AC的表达式为:y=﹣x+4,
同理可得:PC=,
设点P(n,﹣n+4),则n2+(4﹣n﹣4)2=,
解得:n=1或﹣,
故点P(1,)或(﹣,5);
综上,点P的坐标为P(,4)或(0,)或(1,)或(﹣,5).
11.解:(1)y=﹣(x+2)(x﹣m)(m>0),令y=0,则x=﹣2或m,
故点B、C的坐标分别为:(﹣2,0)、(m,0);
(2)存在,理由:
y=﹣(x+2)(x﹣m),令x=0,则y=2,故点E(0,2),
△BCE的面积=×BC×OE=(m+2)×2=6,解得:m=4,
则抛物线的对称轴为:x=(﹣2+4)=1,
点B关于函数对称轴的对称点为点C(m,0),连接CG交对称轴于点H,则点H为所求,
将点C、G的坐标代入一次函数表达式并解得:
直线CG的表达式为:y=﹣bx+b,当x=1时,y=b,
故点H(1,b);
(3)∵OE=OB=2,故∠EBO=45°,
过点F作FT⊥x轴于点T;
①当△BEC∽△BCF时,
则BC2=BE?BF,∠FBO=EBO=45°,
则直线BF的函数表达式为:y=﹣x﹣2,故点F(x,﹣x﹣2);
将点F的坐标代入抛物线表达式得:﹣x﹣2=﹣(x+2)(x﹣m),
解得:x=﹣2(舍去)或2m,
故点F(2m,﹣2m﹣2),
则BF=2(m+1),BE=2,
∵BC2=BE?BF,
则(m+2)2=22(m+1),解得:m=2±2(舍去负值),
故m=2+2;
②当△BEC∽△FCB时,
则BC2=BF?EC,∠CBF=∠ECO,
则△BFT∽△COE,
则,则点F[x,﹣(x+2)],
将点F的坐标代入抛物线表达式得:﹣(x+2)=﹣(x+2)(x﹣m),
解得:x=﹣2(舍去)或m+2;
则点F[m+2,﹣(m+4)]
BC2=BF?EC,则(m+2)2=?,
化简得:m3+4m2+4m=m3+4m2+4m+16,
此方程无解;
综上,m=2.
12.解:(1)把B(﹣1,0)代入抛物线解析式得,
(﹣1+2)2+m=0,
解得m=﹣1,
∴抛物线的解析式为y=(x+2)2﹣1,
当y=0时,(x+2)2﹣1=0,解得x1=﹣1,x2=﹣3,
∴A(﹣3,0).
当x=0时,y=(x+2)2﹣1=3,
∴C(0,3)
∵抛物线对称轴是直线x=﹣2,C,D两点关于抛物线对称轴对称,
∴D(﹣4,3);
(2)△ABM是等腰直角三角形;
证明:∵抛物线y=(x+2)2﹣1的顶点是M,
∴M(﹣2,﹣1),
作MN⊥x轴于N,则N(﹣2,0).
∴AN=BN=MN=1,
∴AM=BM,
tan∠MAN=tan∠MBN=1,
∴∠MAN=∠MBN=45°,
∴∠AMB=180°﹣∠MAN﹣∠MBN=90°,
∴△ABM是等腰直角三角形;
(3)存在,理由:
①当△ABD∽△PDC时,
,即:,
则PD=,
过点P分别作x、y轴的垂线交于点M、N,
则PM=PD=×==DM,
则点P(,);
②当△ABD∽△CDP时,
同理可得:点P(2,﹣3)
综上,点P(,)或P2(2,﹣3).
13.解:(1)∵一次函数y=kx+2的图象经过点,
∴=k+2,
∴k=,
∴一次函数的解析式为:y=x+2,
∵一次函数y=x+2的图象与x轴相交于点A,与y轴相交于点B,
∴点A(﹣4,0),点B(0,2);
(2)∵二次函数y=ax2+bx(a>0)的图象经过点A和点P,
∴
解得:
∴二次函数解析式为:y=x2+2x
∵y=x2+2x=(x+2)2﹣2
∴顶点M坐标(﹣2,﹣2)
(3)∵对称轴与一次函数的图象相交于点N.
∴点N(﹣2,1),
∵点N(﹣2,1),点M(﹣2,﹣2),点P(1,),点B(0,2),
∴MN=3,NP=,BP=,
∵MN∥y轴,
∴∠PBO=∠PNM,即点Q只能在点B下方,
∵△PNM和△PBQ相似,
∴或
∴,或
∴BQ=1,或BQ=,
∴点Q(0,1)或(0,).
14.解(1)∵点A(﹣1,0),E(1,﹣4)在抛物线y=ax2+bx﹣3上,
∴,
解得:,
∴抛物线的解析式为y=x2﹣2x﹣3;
(2)如图1,∵A(﹣1,0),
∴OA=1,
∵OD=OA,
∴OD=1,∴D(0,1),
∵E(1,﹣4),
∴OD=1,OB=3,,,,
∵,,,
∴,
∴△BOD~△BCE,
∴∠DBO=∠EBC,
∴∠α﹣∠β=∠DBC﹣∠CBE=∠DBC﹣∠DBD=∠CBO,
∴sin(α﹣β)=;
(3)由(2)值,△BOD∽△BCE,
∴∠BCE=∠BOD=90°,
∵△BOD为直角三角形,
∵以P、A、C三点为顶点的三角形与△BCE相似,
则以P、A、C为顶点的三角形必为直角三角形,如图2,
①以A为直角顶点时,∠CAP1=90°=∠AOC,
∴∠OAP1+∠CAO=90°,
∵∠OAP1+∠OP1A=90°,
∴∠CAO=∠AP1O,
∵∠AOP1=∠COA=90°,
∴△AOC∽△P1OA,
∴
∴OA2=OC?OP1,
∵抛物线的解析式为y=x2﹣2x﹣3,
∴C(0,﹣3),
∴OC=3,
∵OA=1,
∴12=3×OP1,
∴
∴
②以C为直角顶点时,同①的方法得,OC2=OA?OP2
即:9=1×OP2
∴OP2=9
∴P2(9,0)
③以P为直角顶点时,P3(0,0)
综上所述:满足条件的P点有,P2(9,0),P3(0,0).
与相似三角形相关的压轴题(附答案)
方法提炼:
1、求一点使两个三角形相似的问题,我们可以先找出可能相似的三角形,一般是有几种情况,需要分类讨论,然后根据两个三角形相似的边长相似比来求点的坐标。
典例引领:
例:如图,直线y=-x+3交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c经过A、B、C(1,0)三点。
(1)求抛物线的解析式;?
(2)若点D的坐标为(-1,0),在直线y=-x+3上有一点P,使ΔABO与ΔADP相似,求出点P的坐标;
解:(1)抛物线的解析式为y=x2-4x+3
(2)由题意可得:△ABO为等腰三角形, ? ?
若△ABO∽△AP1D ,则=? ? ??
∴DP1=AD=4??,?∴P1(1,4)
若△ABO∽△ADP2?,过点P2作P2?M⊥x轴于M,AD=4,?
∵△ABO为等腰三角形,?∴△ADP2是等腰三角形,由三线合一可得:DM=AM=2=?P2M,
?即点M与点C重合???,∴P2(1,2)
跟踪训练:
1.如图,在平面直角坐标系xOy中,抛物线与x轴相交于点A(﹣2,0)、B(4,0),与y轴交于点C(0,﹣4),BC与抛物线的对称轴相交于点D.
(1)求该抛物线的表达式,并直接写出点D的坐标;
(2)过点A作AE⊥AC交抛物线于点E,求点E的坐标;
(3)在(2)的条件下,点F在射线AE上,若△ADF∽△ABC,求点F的坐标.
2.如图1,已知二次函数y=ax2﹣a(a为常数,且a≠0)与x轴交于A、B,与y轴的交点为C.过点A的直线l:y=kx+b(k,b为常数,且k≠0)与抛物线另一交点为E,交y轴于D.
(1)用含k的式子表示直线l的解析式;
(2)若a=3,k=,点P为抛物线上第四象限上的一动点,过P作y轴的平行线交AD于M,作PN⊥AD于N,当△PMN面积有最大值时,求点P的坐标;
(3)如图2,若a=3,k=1,连结AC、BC,在坐标平面内,求使得△ACD与△BCQ相似(其中点Q与点A是对应顶点)的Q的坐标.
3.如图1,抛物线y=ax2﹣6ax+6(a≠0)与x轴交于点A(8,0),与y轴交于点B,在x轴上有一动点E(m,0)(0<m<8),过点E作x轴的垂线交直线AB于点N,交抛物线于点P,过点P作PM⊥AB于点M.
(1)求出抛物线的函数表达式;
(2)设△PMN的面积为S1,△AEN的面积为S2,若S1:S2=36:25,求m的值;
(3)如图2,在(2)条件下,将线段OE绕点O逆时针旋转得到OE′,旋转角为30°,连接E'A、E'B,在坐标平面内找一点Q,使△AOE′~△BOQ,并求出Q的坐标.
4.如图1,以点A(﹣1,2)、C(1,0)为顶点作Rt△ABC,且∠ACB=90°,tanA=3,点B位于第三象限
(1)求点B的坐标;
(2)以A为顶点,且过点C的抛物线y=ax2+bx+c(a≠0)是否经过点B,并说明理由;
(3)在(2)的条件下(如图2),AB交x轴于点D,点E为直线AB上方抛物线上一动点,过点E作EF⊥BC于F,直线EF分别交y轴、AB于点G、H,若以点B、G、H为顶点的三角形与△ADC相似,求点E的坐标.
5.抛物线C1:y=ax2+bx+3与x轴交于A(﹣3,0)、B两点,与y轴交于点C,点M(﹣2,3)是抛物线上一点.
(1)求抛物线C1的表达式.
(2)若抛物线C2关于C1关于y轴对称,点A、B、M关于y轴的对称分别为A′、B′、M′.过点M′作M′E⊥x轴于点E,交直线A′C于点D,在x轴上是否存在点P,使得以A′、D、P为顶点的三角形与△AB′C相似?若存在,请求出点P的坐标;若不存在,请说明理由.
6.如图,已知抛物线经过点A(﹣1,0),B(2,0),C(0,2),点D为OC中点,连接AC、BD,并延长BD交AC于点E.
(1)求抛物线w1的表达式;
(2)若抛物线w1与抛物线w2关于y轴对称,在抛物线w2位于第二象限的部分上取一点Q,过点Q作QF⊥x轴,垂足为点F,是否存在这样的F点,使得△QFO与△CDE相似?若存在,求出点F的坐标,若不存在,请说明理由.
7.在平面直角坐标系中,如图1,抛物线y=ax2+bx+c的对称轴为x=,与x轴的交点A(﹣1,0)与y轴交于点C(0,﹣2).
(1)求抛物线的解析式;
(2)如图2.点P是直线BC下方抛物线上的一点,过点P作BC的平行线交抛物线于点Q(点Q在点P右侧),连结BQ,当△PCQ的面积为△BCQ面积的一半时,求P点的坐标;
(3)现将该抛物线沿射线AC的方向进行平移,平移后的抛物线与直线AC的交点为A'、C'(点C'在点A'的下方),与x轴的交点为B',当△AB'C'与△AA'B'相似时,求出点A′的横坐标.
8.如图,以D为顶点的抛物线y=﹣x2+bx+c交x轴于A、B两点,交y轴于点C,直线BC的表达式为y=﹣x+3.
(1)求抛物线的表达式.
(2)请你判断△BCD的形状,并说明理由.
(3)在x轴上是否存在一点Q,使得以A、C、Q为顶点的三角形与△BCD相似?若存在,请求出点Q的坐标;若不存在,请说明理由.
9.如图,已知动圆A恒过定点B(0,﹣1),圆心A在抛物线y=﹣x2上运动,MN为⊙A在x轴上截得的弦(点M在点N左侧).
(1)当点A坐标为(,a)时,求a的值,并计算此时⊙A的半径与弦MN的长;
(2)当⊙A的圆心A运动时,判断弦MN的长度是否发生变化?若改变,请举例说明;若不变,请说明理由;
(3)连接BM,BN,当△OBM与△OBN相似时,计算点M的坐标.
10.如图,已知二次函数y=﹣x2+bx+c(b,c为常数)的图象经过点A(3,1),点C(0,4),顶点为点M,过点A作AB∥x轴,交y轴于点D,交该二次函数图象于点B,连结BC.
(1)求该二次函数的解析式及点M的坐标;
(2)若将该二次函数图象向下平移m(m>0)个单位,使平移后得到的二次函数图象的顶点与△ABC的外心重合,求m的取值;
(3)点P是坐标平面内的一点,使得△ACB与△MCP相似,且CM的对应边为AC,请写出所有点P的坐标(直接写出结果,不必写解答过程).
11.如图1,已知抛物线;C1:y=﹣(x+2)(x﹣m)(m>0)与x轴交于点B、C(点B在点C的左侧),与y轴交于点E.
(1)求点B、点C的坐标;
(2)当△BCE的面积为6时,若点G的坐标为(0,b),在抛物线C1的对称轴上是否存在点H,使得△BGH的周长最小,若存在,则求点H的坐标(用含b的式子表示);若不存在,则请说明理由;
(3)在第四象限内,抛物线C1上是否存在点F,使得以点B、C、F为顶点的三角形与△BCE相似?若存在,求m的值;若不存在,请说明理由.
12.如图,抛物线y=(x+2)2+m与x轴交于A,B两点,与y轴交于点C.点D在抛物线上,且与点C关于抛物线的对称轴对称,抛物线的顶点为M,点B的坐标为(﹣1,0).
(1)求抛物线的解析式及A,C,D的坐标;
(2)判断△ABM的形状,并证明你的结论;
(3)若点P是直线BD上一个动点,是否存在以P,C,D为顶点的三角形与△ABD相似?若存在,请直接写出点P的坐标;若不存在,请说明理由
13.已知一次函数y=kx+2的图象经过点,与x轴相交于点A,与y轴相交于点B,二次函数y=ax2+bx(a>0)的图象经过点A和点P,顶点为M,对称轴与一次函数的图象相交于点N.
(1)求一次函数的解析式以及A点,B点的坐标;
(2)求顶点M的坐标;
(3)在y轴上求一点Q,使得△PNM和△PBQ相似.
14.如图,已知抛物线y=ax2+bx﹣3与x轴交于A、B两点,A(﹣1,0)与y轴交于点C,点E(1,﹣4)为抛物线的顶点,且OD=OA.
(1)求抛物线的解析式;
(2)设∠DBC=α,∠CBE=β,求sin(α﹣β)的值;
(3)探究坐标轴上是否存在点P,使得以P、A、C三点为顶点的三角形与△BCE相似,若存在,请指出点P的位置,并直接写出点P的坐标,若不存在,请说明理由.
参考答案
1.解:(1)设抛物线的解析式为y=a(x+2)(x﹣4),将C(0,﹣4)代入得:﹣8a=﹣4,解得:a=,
∴抛物线的解析式为y=x2﹣x﹣4.
如图1所示:记抛物线的对称轴与x轴交点坐标为F.
∵抛物线的对称轴为x=﹣=1,
∴BF=OB﹣OF=3.
∵BO=OC=4,∠BOC=90°,
∴∠OBC=45°.
∴△BFD为等腰直角三角形.
∴FD=FB=3.
∴D(1,﹣3).
(2)如图2,过点E作EH⊥AB,垂足为H.
∵∠EAB+∠BAC=90°,∠BAC+∠ACO=90°,
∴∠EAH=∠ACO.
∴tan∠EAH=tan∠ACO=.
设EH=t,则AH=2t,
∴点E的坐标为(﹣2+2t,t).
将(﹣2+2t,t)代入抛物线的解析式得:(﹣2+2t)2﹣(﹣2+2t)﹣4=t,
解得:t=或t=0(舍去)
∴E(5,).
(3)A、B、C、D四个点坐标分别为:A(﹣2,0),B(4,0),C(0,﹣4),D(1,﹣3),
则:AD=3,AB=6,AC=2,BC=4,
∵△ADF∽△ABC,
∴,
∴,
∴AF=,
设:点F坐标为(x,x+1),
过点F作x轴的垂线交x轴于点H,
则:AF2=FH2+AH2,
即:10=(x+1)2+(x+2)2,
解得:x=﹣2+2或﹣2﹣2(舍去),
故点F坐标为(﹣2+2,).
2.解:(1)∵二次函数y=ax2﹣a(a为常数,且a≠0)与x轴交于A,
∴y=0时,ax2﹣a=0,
解得:x1=1,x2=﹣1,
∴A(﹣1,0),
∵直线l:y=kx+b(k,b为常数,且k≠0)过点A,
∴﹣k+b=0,
∴b=k,
∴直线l的解析式为y=kx+k;
(2)∵a=3,k=,
∴二次函数解析式为y=3x2﹣3,直线l的解析式为y=,
∴D(0,),
∴OA=1,OD=,
∴AD===,
设点P的坐标为(x,3x2﹣3),则点M (x,),
∴PM=,
∵PM∥y轴,
∴∠PMN=∠ADO.
又∵∠PNM=∠AOD=90°,
∴△PMN∽△ADO,
∴,
∴=,
∴当PM有最大值时,S△PMN的面积最大,此时x=,
∴,
∴.
(3)△ACD与△QBC相似,
当a=3,k=1时,二次函数解析式为y=3x2﹣3,直线l的解析式为y=x+1,
∴C(0,﹣3),B(1,0),D(0,1),
∴,CD=4,AC=,BC=,
设点Q坐标为(x,y)
若△ACD∽△QBC,
∴,
∴,
∴,
∴,
解得:,,
∴Q点的坐标为()或;
若△ACD∽△QCB,
∴,
∴,
∴,
∴,
解得:或,
∴Q点的坐标为(0,﹣)或(),
综上所述:点Q坐标为:或或或().
3.解:(1)把A(8,0)代入y=ax2﹣6ax+6,得64a﹣48a+6=0,解得a=,
∴抛物线的函数表达式为:y=x2+x+6;
(2)如图1,在y=x2+x+6中,令x=0,得y=6,
∴B(0,6),
设直线AB解析式为y=kx+b,则,解得
∴直线AB解析式为y=x+6
∵PE⊥x轴,PM⊥AB
∴∠AEN=∠PMN=90°,
∵∠ANE=∠PNM
∴△ANE∽△PNM
∴==,==()2,
∵S1:S2=36:25,
∴=
∴=,即6AN=5PN
∵E(m,0)(0<m<8),
∴P(m,+m+6),N(m,m+6)
∴EN=m+6,PN=PE﹣EN=+m+6﹣(m+6)=+3m
OE=m,AE=8﹣m,
∵AB===10
∴cos∠OAB==,即=
∴AN=(8﹣m),
∴6×(8﹣m)=5×(+3m),解得:m1=4,m2=8(不符合题意,舍去),
∴m=4;
(3)如图2,∵线段OE绕点O逆时针旋转得到OE′,旋转角为30°,
∴OE′=OE=4,∠AOE′=30°
∵△AOE′~△BOQ,
∴=,∠BOQ=∠AOE′=30°,
∴=,即OQ=3,过点Q作QH⊥y轴于H,
∴QH=OQ=,OH===,
∴当点Q在y轴右侧时,Q1(,),
当点Q在y轴左侧时,Q2(﹣,).
综上所述,Q的坐标为:Q1(,),Q2(﹣,).
4.解:(1)过C点作MN垂直x轴.过A、B两点分别作AM⊥MN,垂足为M,BN⊥MN,垂足为N,
∵∠ACB=90°,
∴∠CBN=∠ACM,
∴△CNB~△AMC,
∴,
∵A(﹣1,2)、C(1,0),
∴AM=2,CM=2,
又∵tanA==3,
∴BN=6,CN=6,
∴B点坐标为(﹣5,﹣6).
(2)设以A(﹣1,2)为顶点的抛物线为y=a(x+1)2+2,
∵抛物线经过C(1,0)
∴a(1+1)2+2=0,
∴,
∴函数解析式为,
当x=﹣5时,y==﹣6,
∴以A为顶点,且过点C的抛物线为经过点BB(﹣5,﹣6).
(3)∵点A(﹣1,2)、C(1,0),
∴直线yAC=﹣x+1,∠ACD=45°,
∵EF⊥BC,
∴∠BHC=DAC,
∴以点B、G、H为顶点的三角形与△ADC相似,有两种情况:
Ⅰ.如图2(1).∠HGB=45°,∵EG∥AC,∴BG∥CD,即BG⊥y轴,
∴G坐标为(0,﹣6)
∴直线yEG=﹣x﹣6,
依题意得:,
解得(不合题意舍去),得,
∴当∠HGB=∠ACD=45°时△HBG∽ADC,即:E点坐标为().
Ⅱ.如图2(2).∠HBG=∠ACD=45°时,△HBG∽△ACD,
∵过B点作BP⊥y轴,∴P点(0,﹣6)
∵∠CBP=45°,
∴∠GBP=∠ABC,
又∵tan∠GBP=,tan∠ABC=,BP=5,
∴GP=,即G点坐标为(0,),
∴直线,
依题意得:,
解得,(不合题意舍去),得,
即E点为(,),
综上所述:E点坐标为()或(,),
5.解:(1)将点A、M的坐标代入函数表达式得:,解得:,
故抛物线C1的表达式为:y=﹣x2﹣2x+3;
(2)由题意得:点A(﹣3,0)、B(1,0)、C(0,3)、M(﹣2,3)、B′(﹣1,0)、A′(3,0),D(2,1),
则AB′=2,AC=3,B′C=,A′D=,
①当点P在直线AC的左侧时,
当点P在DM′左侧时,
A′、D、P为顶点的三角形与△AB′C相似,
则△AB′C∽△A′DP,则,
即:,解得:A′P=3,
故点P(0,0),
当点P在DM′左侧时,
同理可得点P(P′)(,0);
②当点P在直线AC的右侧时,
则△AB′C、△DA′P″不相似,
综上,点P的坐标为(0,0)或(,0).
6.解:(1)设抛物线的解析式为y=ax2+bx+c,将A(﹣1,0),B(2,0),C(0,2)代入抛物线的解析式得:
,
解得:,
∴抛物线w1的表达式为y=﹣x2+x+2;
(2)∵抛物线w1与抛物线w2关于y轴对称,
∴抛物线w2的解析式y=﹣x2﹣x+2,
∵点D为OC中点,C(0,2),
∴D(0,1),
∵A(﹣1,0),B(2,0),
∴,
∵∠AOC=∠BOD=90°,
∴△AOC∽△DOB,
∴∠ACO=∠DBO,
∴BD⊥AC,
∴,
设F(a,0),Q(a,﹣a2﹣a+2),a<0,若△QFO与△CDE相似,可分两种情况考虑:
①△QFO与∽△CED时,
,
∴,
解得:a1=﹣1,a2=2(舍去),
∴F(﹣1,0);
②△QFO∽△DEC时,
,
∴,
解得:,(舍去),
∴F(,0).
综合以上可得F点的坐标为F(﹣1,0)或F(,0).
7.解:(1)由对称性可知B(4,0)
设抛物线解析式为y=a(x+1)(x﹣4)
将(0,﹣2)代入得a=
∴y=x2﹣x﹣2.
(2)由平行线间距离处处相等可知,当△PCQ的面积为△BCQ面积的一半时,PQ=BC
∵C(0,﹣2),B(4,0)
∴BC=
∴PQ=
∴PQ2=+=5
∵直线BC的解析式为y=x﹣2,PQ∥BC
∴设直线PQ的解析式为y=x+b
则yP=xP+b,yQ=y=xQ+b
联立得
x2﹣4x﹣4﹣2b=0
则xP+xQ=4
∵PQ2=+=5
∴=5,xQ﹣xP=2
∴点P(1,﹣3)
(3)由点A(﹣1,0),C(0,﹣2)得直线AC的解析式为y=﹣2x﹣2
设点A'坐标为(a,﹣2a﹣2),由平移的性质,可知AC=A'C'=
平移距离为AA'=(a+1)
∴AC'=(a+2)
当△AB'C'与△AA'B'相似时,只有当△AB'C'∽△AA'B'
∴AB'2=AA'×AC'=5(a+1)(a+2)
过点B'作AA'的平行线,交原抛物线于点D,连接AD,
由平移知四边形ADB'A'为平行四边形,点D的纵坐标为2a+2
设点D的横坐标为m,则点B'坐标为(m+a+1,0)
∴AB'2=(m+a+2)2=5(a+1)(a+2),①
将点D(m,2a+2)代入y=x2﹣x﹣2得
﹣﹣2=2a+2,②
联立①②,解得:a=,
m2﹣9m+15=0,
∴m=,或m=(舍)
∴a═==
∴点A′的横坐标为.
8.解:(1)把x=0代入y=﹣x+3,得:y=3,
∴C(0,3)
把y=0代入y=﹣x+3,得:x=3,
∴B(3,0)
将C(0,3)、B(3,0)代入y=﹣x2+bx+c得:,
解得
∴抛物线的解析式为y=﹣x2+2x+3;
(2)△BCD是直角三角形,理由如下:
由y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴D(1,4)
又∵C(0,3)、B(3,0)、D(1,4),
∴CD==,BC==3,DB==2
∵()2+(3)2=20,(2)2=20,
∴CD2+BC2=BD2,
∴∠BCD=90°.即△BCD是直角三角形;
(3)如图,连接AC,把y=0代入y=﹣x2+2x+3,
解得:x=﹣1或x=3,
∴A(﹣1,0),
∴OA=1,
∴=,
∵=,
∴,
又∵∠AOC=DCB=90°,
∴△AOC∽△DCB.
∴当Q的坐标为(0,0)时,△AQC∽△DCB,
过点C作CQ⊥AC,交x轴与点Q.
∵△ACQ为直角三角形,CO⊥AQ,
∴△ACQ∽△AOC.
又∵△AOC∽△DCB,
∴△ACQ∽△DCB,
∴,即,
解得:AQ=10.
∴Q(9,0).
综上所述,当Q的坐标为(0,0)或(9,0)时,以A、C、Q为顶点的三角形与△BCD相似.
9.解:(1)把点A()代入得,
a=﹣,
∵B(0,﹣1),
∴AB∥x轴,
∴⊙A的半径为,
如图1,过点A作AE⊥MN于点E,连接AM,
则AM=AB=,
∴ME===1,
由垂径定理,MN=2ME=2×1=2.
故此时⊙A的半径为,弦MN的长为2;
(2)MN不变.如图2,理由如下:
设点A(m,n),则AB2=m2+(n+1)2,
在Rt△AME中,ME2=AM2﹣AE2=m2+(n+1)2﹣n2=m2+2n+1,
∵点A在抛物线y=﹣x2上,
﹣m2=n,
将n=﹣代入ME2=m2+2n+1得,
ME2=1,
ME=1,
由垂径定理得,MN=2ME=2×1=2(是定值,不变);
(3)由(2)知MN=2,
设M(x,0),则N(x+2,0).
当△OBM与△OBN相似,有以下情况:
①M、N在y轴同侧,
∵△OBM与△OBN相似,
∴,
即OB2=OM?ON,
∴x(x+2)=1,
整理得,x2+2x﹣1=0,
解得:,
∴当M、N在y轴右侧时,M(﹣1+,0),
当M、N在y轴左侧时,M(﹣1﹣,0),
②M、N在y轴两侧时,
∵△OBM与△OBN相似,
∴,
即OB2=OM?ON,
﹣x(x+2)=1,
整理得,x2+2x+1=0,
解得x=﹣1,
此时△OBM与△OBN全等,M(﹣1,0),
综合以上可得,M点的坐标为(﹣1+,0)或(﹣1﹣,0)或(﹣1,0).
10.解:(1)C(0,4),则c=4,抛物线表达式为:y=﹣x2+bx+4,
将点A的坐标代入上式并解得:b=2,
故抛物线的表达式为:y=﹣x2+2x+4,
则点M(1,5);
(2)点A(3,1)函数的对称轴为:x=1,则点B(﹣1,1),点C(0,4),
直线BC的中点坐标为:(﹣,),
则线段BC的中垂线的函数表达式为:y=﹣x+,
当x=1时,y=2,即外心坐标为(1,2),
则二次函数图象向下平移了5﹣2=3个单位;
(3)△ACB与△MCP相似,且CM的对应边为AC,存在△ACB∽△CMP或△CAB∽△CMP,
点A、B、C、M的坐标分别为:(3,1)、(﹣1,1)、(0,4)、(1,5),
则AB=4,BC=,AC=3,CM=,
①当△ACB∽△CMP时,如下图左侧图,
则,即,
解得:PM=,PC=,
设点P(r,s),
则r2+(s﹣4)2=,(r﹣1)2+(s﹣5)2=,
解得:r=,s=4或r=0,s=
故点P(,4)或(0,);
②当△CAB∽△CMP时,如上图右侧图,
则点P在直线CA上,直线AC的表达式为:y=﹣x+4,
同理可得:PC=,
设点P(n,﹣n+4),则n2+(4﹣n﹣4)2=,
解得:n=1或﹣,
故点P(1,)或(﹣,5);
综上,点P的坐标为P(,4)或(0,)或(1,)或(﹣,5).
11.解:(1)y=﹣(x+2)(x﹣m)(m>0),令y=0,则x=﹣2或m,
故点B、C的坐标分别为:(﹣2,0)、(m,0);
(2)存在,理由:
y=﹣(x+2)(x﹣m),令x=0,则y=2,故点E(0,2),
△BCE的面积=×BC×OE=(m+2)×2=6,解得:m=4,
则抛物线的对称轴为:x=(﹣2+4)=1,
点B关于函数对称轴的对称点为点C(m,0),连接CG交对称轴于点H,则点H为所求,
将点C、G的坐标代入一次函数表达式并解得:
直线CG的表达式为:y=﹣bx+b,当x=1时,y=b,
故点H(1,b);
(3)∵OE=OB=2,故∠EBO=45°,
过点F作FT⊥x轴于点T;
①当△BEC∽△BCF时,
则BC2=BE?BF,∠FBO=EBO=45°,
则直线BF的函数表达式为:y=﹣x﹣2,故点F(x,﹣x﹣2);
将点F的坐标代入抛物线表达式得:﹣x﹣2=﹣(x+2)(x﹣m),
解得:x=﹣2(舍去)或2m,
故点F(2m,﹣2m﹣2),
则BF=2(m+1),BE=2,
∵BC2=BE?BF,
则(m+2)2=22(m+1),解得:m=2±2(舍去负值),
故m=2+2;
②当△BEC∽△FCB时,
则BC2=BF?EC,∠CBF=∠ECO,
则△BFT∽△COE,
则,则点F[x,﹣(x+2)],
将点F的坐标代入抛物线表达式得:﹣(x+2)=﹣(x+2)(x﹣m),
解得:x=﹣2(舍去)或m+2;
则点F[m+2,﹣(m+4)]
BC2=BF?EC,则(m+2)2=?,
化简得:m3+4m2+4m=m3+4m2+4m+16,
此方程无解;
综上,m=2.
12.解:(1)把B(﹣1,0)代入抛物线解析式得,
(﹣1+2)2+m=0,
解得m=﹣1,
∴抛物线的解析式为y=(x+2)2﹣1,
当y=0时,(x+2)2﹣1=0,解得x1=﹣1,x2=﹣3,
∴A(﹣3,0).
当x=0时,y=(x+2)2﹣1=3,
∴C(0,3)
∵抛物线对称轴是直线x=﹣2,C,D两点关于抛物线对称轴对称,
∴D(﹣4,3);
(2)△ABM是等腰直角三角形;
证明:∵抛物线y=(x+2)2﹣1的顶点是M,
∴M(﹣2,﹣1),
作MN⊥x轴于N,则N(﹣2,0).
∴AN=BN=MN=1,
∴AM=BM,
tan∠MAN=tan∠MBN=1,
∴∠MAN=∠MBN=45°,
∴∠AMB=180°﹣∠MAN﹣∠MBN=90°,
∴△ABM是等腰直角三角形;
(3)存在,理由:
①当△ABD∽△PDC时,
,即:,
则PD=,
过点P分别作x、y轴的垂线交于点M、N,
则PM=PD=×==DM,
则点P(,);
②当△ABD∽△CDP时,
同理可得:点P(2,﹣3)
综上,点P(,)或P2(2,﹣3).
13.解:(1)∵一次函数y=kx+2的图象经过点,
∴=k+2,
∴k=,
∴一次函数的解析式为:y=x+2,
∵一次函数y=x+2的图象与x轴相交于点A,与y轴相交于点B,
∴点A(﹣4,0),点B(0,2);
(2)∵二次函数y=ax2+bx(a>0)的图象经过点A和点P,
∴
解得:
∴二次函数解析式为:y=x2+2x
∵y=x2+2x=(x+2)2﹣2
∴顶点M坐标(﹣2,﹣2)
(3)∵对称轴与一次函数的图象相交于点N.
∴点N(﹣2,1),
∵点N(﹣2,1),点M(﹣2,﹣2),点P(1,),点B(0,2),
∴MN=3,NP=,BP=,
∵MN∥y轴,
∴∠PBO=∠PNM,即点Q只能在点B下方,
∵△PNM和△PBQ相似,
∴或
∴,或
∴BQ=1,或BQ=,
∴点Q(0,1)或(0,).
14.解(1)∵点A(﹣1,0),E(1,﹣4)在抛物线y=ax2+bx﹣3上,
∴,
解得:,
∴抛物线的解析式为y=x2﹣2x﹣3;
(2)如图1,∵A(﹣1,0),
∴OA=1,
∵OD=OA,
∴OD=1,∴D(0,1),
∵E(1,﹣4),
∴OD=1,OB=3,,,,
∵,,,
∴,
∴△BOD~△BCE,
∴∠DBO=∠EBC,
∴∠α﹣∠β=∠DBC﹣∠CBE=∠DBC﹣∠DBD=∠CBO,
∴sin(α﹣β)=;
(3)由(2)值,△BOD∽△BCE,
∴∠BCE=∠BOD=90°,
∵△BOD为直角三角形,
∵以P、A、C三点为顶点的三角形与△BCE相似,
则以P、A、C为顶点的三角形必为直角三角形,如图2,
①以A为直角顶点时,∠CAP1=90°=∠AOC,
∴∠OAP1+∠CAO=90°,
∵∠OAP1+∠OP1A=90°,
∴∠CAO=∠AP1O,
∵∠AOP1=∠COA=90°,
∴△AOC∽△P1OA,
∴
∴OA2=OC?OP1,
∵抛物线的解析式为y=x2﹣2x﹣3,
∴C(0,﹣3),
∴OC=3,
∵OA=1,
∴12=3×OP1,
∴
∴
②以C为直角顶点时,同①的方法得,OC2=OA?OP2
即:9=1×OP2
∴OP2=9
∴P2(9,0)
③以P为直角顶点时,P3(0,0)
综上所述:满足条件的P点有,P2(9,0),P3(0,0).
同课章节目录
